基于目标端影响模型与次模性的预算分配博弈问题分析❋

农庆琴， 王媛媛

(中国海洋大学数学科学学院， 山东 青岛 266100)

随着商品的市场竞争越来越激烈，商品品牌的营销策略也越来越重要。商家在媒体渠道投放广告是商品品牌营销的一个重要手段，例如：服装品牌商通过在广告牌、电视台、网购平台等媒体渠道投放广告来影响消费者，期望他们变成商品的购买者。然而，品牌商的推广预算有限，如何将有限的预算在电视、报纸和网络等媒体渠道进行分配，才能最大限度地影响潜在客户，达到增加销售的目的，这是品牌营销需要解决的重要问题。

2012年Alon等[1]研究了品牌商如何通过在媒体渠道投放广告(分配预算)的问题，提出了两个影响模型：源端影响模型(Source-side influence model)和目标端影响模型(Target-side influence model)，将预算约束下的分配问题表述成目标为被激活客户的期望数量最大化的优化问题。

在现实情况中，对于客户而言，多数情况下影响其购买欲的原因不在于通过何种渠道看到广告，而在于他们看到的广告本身。由此看来，目标端影响模型虽然复杂，但它更贴近现实中的广告传播过程。因此，本文对文献[1]中提出的目标端影响模型进行调整——假设同一个物品的广告不管消费者是第几次看到它，该物品的吸引力都是相同的；并基于调整后的影响模型来研究预算分配影响最大化问题。

Alon[1]探讨的问题的前提假设是在市场中只有单个品牌商，然而在现实的渠道市场中，通常有许多拥有同类可比产品的品牌商，他们彼此竞争，都想通过在媒体渠道投放广告的营销方式将潜在客户转化为自己的忠实买家。在这种场景下，多个品牌商竞争情况下的预算分配问题形成了一个非合作博弈问题，各品牌商即为博弈的局中人，他们均是独立、理性的，只在乎个体效用是否最优而不在乎全局效用是否最优。在没有管理机构的情况下，这些品牌商自私的行为结果能给社会带来多少效用？能否实现“社会最优”？要研究这些问题就需要分析缺乏管理者协调的代价，也就是系统的效率。

1999年Koutsoupias和Papadimitriou[7]提出用最佳社会效用和最差纳什均衡下社会效用之间的比值来衡量系统的效率，这个比值称为“无秩序代价”(Price of anarchy，PoA)。2015年Maehara等[8]扩展了文献[1]中的源端影响模型，将单个品牌商的预算分配问题推广到多个品牌商的预算分配问题，并且分析了纳什均衡的存在性及无秩序代价。Hatano等[9]从匹配者的角度探究了将媒体渠道分配给多个品牌商的问题，提出了一种基于拉格朗日分解的算法。2019年Sessa等[10]研究了基于源端影响模型的连续预算分配博弈，证明了PoA至少是2。

1 预备知识

1.1 整数格上的次模函数

f(x)+f(y)≥f(x∨y)+f(x∧y),

其中(x∨y)i=max{xi,yi}，(x∧y)i=min{xi,yi}，i∈[n]，则称函数f为整数格上的次模函数。

易知，整数格上的次模函数的非负组合仍是次模函数。

如果函数f是整数格上的次模函数，则称-f为整数格上的超模函数。

f(x+es)-f(x)≥f(x+2es)-f(x+es)，

其中es表示在分量s处值为1、在其余分量处值为0的|V|维单位向量，则称函数f满足分量凹性。

1.2 纳什均衡

策略式的n人博弈(简称“博弈”)可以用三元组([n],{Si}i∈[n],{fi}i∈[n])表示，其中[n]={1,…,n}为局中人的集合，Si表示局中人i的策略空间，令S=S1×…×Sn为局势集合；fi:S→R是局中人i的个人效用函数。每个局中人i具有个人理性的，其目标是最大化自己的效用函数fi。给定局势s=(s1,…,sn)∈S，记si=(s1,…,si,0,…，0)，S-i=(s1,…,si-1,si+1,…，sn)。

定义3(纳什均衡)[13]在博弈局势s=(s1,…,sn)∈S下，如果对于任意一个局中人i，都满足以下不等式

fi(si,s-i)≥fi(s′i,s-i)， ∀s′i∈Si，

则称局势S是一个纳什均衡。

由纳什均衡的定义可以看出:在纳什均衡局势下，任何局中人都不能通过单独改变自己的策略获得更好的收益，因此，纳什均衡是非合作博弈的一个稳定局势。

2 基于目标端影响模型的预算分配问题

2012年Alon等[1]研究了品牌商通过在媒体渠道投放广告向潜在客户推广产品的问题，分析了媒体渠道分配问题，提出了目标端影响模型。

2.1 目标端影响模型(Target-side influence model)

本节对初始的目标端模型进行调整——假设客户t每次看到广告时被激活的概率相同，记为pt。这个假设来源于广告传播的实际情况：同一个物品的广告不管消费者是第几次看到它，该物品的吸引力都是相同的，所以对于消费者的影响概率也是相同的。

在目标端影响模型下，品牌商的效用函数为：

2.2 基于目标端影响模型的预算分配问题(Channel advertising budget allocation problem)

品牌商在预算限制下从各渠道之间选择一个投放广告分配x，从而激活(或受影响)的最多客户数量f(x)。该问题可描述为以下规划：

满足以上约束的分配x称为可行分配。

接下来，对该规划目标函数的性质进行分析。

引理1基于目标端影响模型的预算分配问题的目标函数f(x)是整数格上的次模函数。

证明 令g(x)=(1-pt)xt≥0,下面证明g(x)是一个整数格上的超模函数。

对于任意的可行分配x=(x(s1),…,x(sk)),y=(y(s1),…,y(sk)),有

x∧y=(x(s1)∧y(s1),…,x(sk)∧y(sk))，

x∨y=(x(s1)∨y(s1),…,x(sk)∨y(sk))，

则有

(x∧y)t=∑s∈γ(t)(x(s)∧y(s))，

(x∨y)t=∑s∈γ(t)(x(s)∨y(s))=
∑s∈γ(t)[(x(s)+y(s))-(x(s)∧y(s))]=
xt+yt-(x∧y)t，

g(x∧y)=(1-pt)(x∧y)t，

即g(x)满足超模函数定义，从而P(x,t)=1-g(x)=1-(1-pt)xt是次模函数。由于次模函数的非负组合仍然是次模函数，因此，f(x)=∑t∈T(1-(1-pt)xt)是整数格上的次模函数。

引理2基于目标端模型的预算分配问题的目标函数f(x)满足分量凹性。

证明 设x,x+es,x+2es均为可行分配。

若(s,t)∉E,f(x+2es)=f(x+es)=f(x),则(f(x+es)-f(x))-(f(x+2es)-f(x+es))=0。

若(s,t)∈E，易知(x+es)t=xt+1，(x+2es)t=xt+2。

因此，基于目标端模型的预算分配问题的目标函数f(x)满足分量凹性。

3 基于目标端影响模型的预算分配博弈

在现实的媒体渠道市场中，通常有许多拥有同类可比产品的品牌商，他们彼此竞争，都想通过在媒体渠道投放广告的营销方式将潜在客户转化为自己的忠实买家。从而，理性的品牌商面对激烈的市场竞争，需要对复杂的竞争市场进行合理的策略博弈分析。本节将单个品牌商的预算分配问题推广到多个品牌商竞争情形——基于目标端模型的预算分配博弈。

当多个品牌商同时尝试激活客户t时，他们将以随机顺序激活客户t，激活规则是先入为主。记[n]排列集合为Δn，对于任意局势x=(x1,x2,…,xn),考虑一个随机排序τ∈Δn，所有品牌商按照τ中的排序依次尝试激活t。品牌商i激活客户t的概率是Pi(xi,t)∏jτi(1-Pj(xj,t)),即在排序τ中排在i前面的品牌商都激活失败而i激活成功的概率。品牌商i的个人效用函数可以表示为

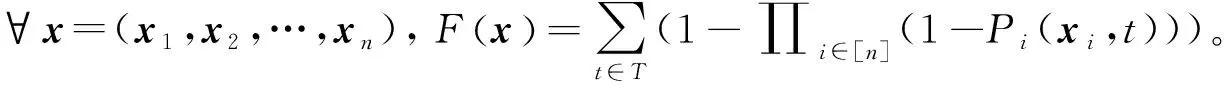
3.1 纯纳什均衡的存在性

纳什均衡是博弈中的一个稳定局势。对于品牌商来说，当目前配置不是纳什均衡时，他就可以通过改变自己的策略来提高他的效用。1951年Nash[13]证明了有限非合作n人博弈存在纳什均衡。这里的纳什均衡指的是混合策略纳什均衡，并不能证明纯策略纳什均衡的存在性，而博弈中是否存在纯策略纳什均衡是一直以来的研究热点。下面探讨基于目标端影响模型的预算分配博弈是否存在纯策略纳什均衡。

1996年Shapley等[14]提出了一类特殊的博弈类型——势博弈(Potential games)，并且证明了此类博弈一定存在纯纳什均衡。下面将通过证明基于目标端影响模型的预算分配博弈是势博弈来证明它一定存在纯策略纳什均衡。

定义4(势博弈)[14]在博弈([n],{Si}i∈[n],{fi}i∈[n])中，如果存在函数p:S→R，对于所有的i∈[n]，s∈S，都有下列等式成立

fi(si,s-i)-fi(s′i,s-i)=
p(si,s-i)-p(s′i,s-i)，s′i∈Si，

则称函数p为博弈的势函数，该博弈称为势博弈。

定理1[14]所有的势博弈都存在纯策略纳什均衡。

定理2基于目标端影响模型的预算分配博弈是势博弈，从而存在纯策略纳什均衡。

对于每一个i∈[n],x-i=(x1,…,xi-1,xi+1,…,xn)，

p(xi,x-i)-p(x′i,x-i)=

fi(xi,x-i)-fi(x′i,x-i)=

(1)

由此可得

因此函数p(x)是基于目标端影响模型的预算分配博弈的势函数。从而，基于目标端影响模型的预算分配博弈是一个势博弈，一定存在纯策略纳什均衡。

3.2 基于目标端影响模型的预算分配博弈的无秩序代价

2015年Maehara等[8]将文献[15]中的有效效用系统(Valid utility system)扩展到整数格中，称一个博弈为整数格上的单调有效效用系统(Monotone utility system on the integer lattice)，如果该博弈满足下列三个条件：

(1)社会效用函数是整数格上的次模函数并且满足分量凹性；

(2)局中人i的个人效用至少是i参与博弈与不参与博弈带来的社会效用的变化量；

(3)所有局中人的个人效用之和不高于社会效用。

Maehara等[8]同时证明了整数格上的单调有效效用系统的无秩序代价至多为2。

定义5(无秩序代价PoA)在非合作博弈中，当纯策略纳什均衡存在时，称最佳社会效用和最差纯纳什均衡的社会效用之间的比值为无秩序代价，记为

其中,L为非合作博弈的所有实例，OPT(I)为实例I的最佳社会效用。

定理3[8]整数格上的单调有效效用系统的无秩序代价PoA≤2。

定理4基于目标端影响模型的预算分配博弈是一个整数格上的单调有效效用系统，它的无秩序代价至多为2。

证明 首先，设激活序列τ={τ1,τ2,…,τn}∈Δn，

所以，预算分配博弈满足条件(2)。

其次，由引理1可知Pi(xi,t)是整数格上的次模函数，那么1-Pi(xi,t)就是整数格上的超模函数。Topkis在文献[12]中证明了整数格上的超模函数的乘积仍然是整数格上的超模函数，所以∏i∈[n](1-Pi(xi,t))仍然是超模函数，那么F(x)则是整数格上的次模函数。因为fi(x)是满足分量凹性的单调递减函数(证明同引理2)，其非负组合也是满足分量凹性的单调递减函数，故F(x)=∑t∈T(1-∏i∈[n](1-Pi(xi,t)))也满足分量凹性且单调递增。所以，预算分配博弈满足条件(1)。

最后，设函数

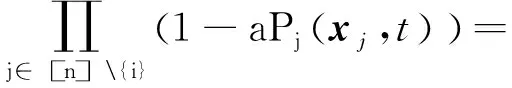
显然，Si(x,t;a)≥0，∀a∈[0,1]。

断言：当a∈[0,1],函数Si(x,t;a)是关于变量a的单调递减函数。

下面证明断言的正确性。已知lnSi(x,t;a)与Si(x,t;a)的单调性相同，由lnSi(x,t;a)的单调性可以得到Si(x,t;a)的单调性。令

由断言可知min{Si(x,t;a),a∈[0,1]}=Si(x,t;1)。

下面讨论fi(x)和F(xi,x-i)-F(0,x-i)的关系。由F(x)的定义可得

由定理2的证明中的(1)式可得

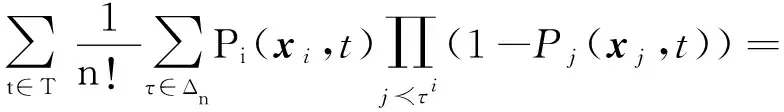
所以，预算分配博弈满足条件(3)。

综上所述，基于目标端影响模型的预算分配博弈是一个整数格上的单调有效效用系统，从而它的无秩序代价至多为2。

4 结语

本文将基于目标端影响模型的单个品牌商的预算分配问题扩展到整数格上，证明了该问题的目标函数是整数格上的单调次模函数；将单个品牌商的目标端影响模型扩展到多个品牌商，提出了基于目标端影响模型的预算分配博弈,证明了该博弈具有纯策略纳什均衡,且该预算分配博弈的无秩序代价至多为2。