非接触式机械密封间隙控制方法及模型研究
周 涛,占宇颉,史伟清
(江苏大学,江苏镇江 212000)
0 引言
由于非接触式机械密封在运行过程中动静环处于不接触状态,具有着端面摩擦磨损小、温升小、使用寿命长等特点,因此在石化、电力、航空航天等工业领域有着广泛应用。其工作原理是通过动(或静)环端面微造型动压槽形成的动压效应使润滑膜开启力增大而保持密封面的非接触,同时通过泵送槽的泵送作用达到减小甚至阻止泄漏的效果。但在非接触式机械密封的实际应用中,常因工况波动、轴系振动等多种因素的影响而导致密封端面间隙的不稳定,可能出现端面流体润滑失效、泄漏增大甚至密封环碰磨损坏等问题。对此,已引起相关专家学者的重视和研究。有文献指出[1],早在20 世纪80年代已经有学者对非接触式密封的动力学响应做出研究,发展至今已经设计出许多新型的密封结构,取得大量的相关理论成果,但在动力学响应领域,学者在研究时大多考虑单一因素对密封结构的影响,没有考虑多种因素耦合带来的影响,因此在面对一些复杂多变的运行工况,这些研究成果难以适用。
综上所述,目前尚缺乏针对非接触机械密封端面间隙主动控制方法、途径等方面的研究,故本文拟针对非接触机械密封端面间隙不稳定问题,基于电磁吸附原理,提出动静环间隙液膜厚度主动控制方案,将电磁力引入密封环受力体系中,通过改变电流调节电磁力大小,消除润滑膜压力变化带来的影响,实现密封动静环间隙的稳定及可控。在非接触机械密封结构基础上,设计密封间隙控制辅助装置。采用ANSYS 软件建立密封间隙液膜内流场数值计算模型并进行仿真计算,结合电磁力计算等对密封环进行受力分析,研究密封间隙与电磁线圈电流的关系并获得相应的计算模型,为密封间隙的主动控制提供参考依据。
1 密封间隙主动控制系统设计
基于磁性吸附原理的非接触式机械密封间隙控制系统如图1 所示,由环形衔铁、电磁铁、距离传感器、信号处理器、控制器、可调直流电源及机械密封组件组成。该密封的静环为补偿环,动环端面开设动压槽,在密封端面运转中产生动压效应,使动静环分离达到非接触目的。辅助控制系统主要对静环的轴向位移进行控制,可以避免辅助控制系统元件受密封介质的温度、压力、腐蚀性等的影响。密封间隙控制系统如图2 所示。

图1 基于磁性吸附的非接触式机械密封控制系统
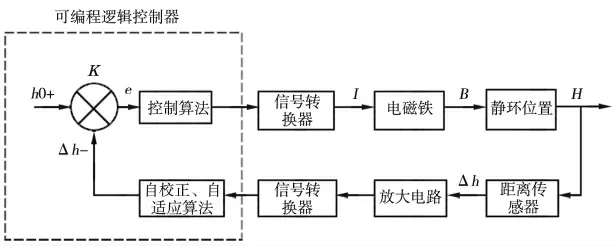
图2 密封间隙控制系统
环形衔铁安装在静环内,在静环和电磁铁间安装弹簧,静环与弹簧座间由O 形圈密封。电磁铁固定于弹簧座上,可为一个或多个,且与静环相隔适当距离。环形衔铁为电磁性材料,在电磁铁通电时与电磁铁产生相互吸引力,以使机械密封运行时在电磁力、弹簧弹力和端面流体作用力的共同作用下形成密封间隙。距离传感器安装于电磁铁壳体上部,进行距离传感器与静环端面之间间距的测量。距离传感器测出自身与静环端面的距离h,信号处理器根据预设定的h0(未接通电源时传感器与静环的距离)算出动、静环端面的间隙Δh。控制器接收信号处理器运算得到的间隙大小Δh,采取PID 控制算法运算得出输出调节信号,依据调节信号控制可调节直流电源输出电流I,改变电磁铁产生的电磁力大小,使静环达到新的平衡位置,最终把密封端面间隙调节到预期大小。
电磁铁在通电后产生磁场,在密封运转中,距离传感器定期测量动静环间的间隙宽度,将间距信号通过放大、矫正后转换成数字信号,并通过PLC 控制器将数字信号转换成电流信号;再通过整流装置改变电磁铁电路中电流的方向和大小,从而改变磁场的方向和大小,以此控制电磁铁与静环上的环形衔铁之间的吸引力和排斥力,借吸引力或排斥力来补偿开启力或闭合力的变化。
2 电磁铁吸附力计算
电磁铁的吸力是基于麦克斯韦基本方程推导出的,因此需假设磁感应强度B 沿磁极表面是均匀分布的,由此得到电磁吸力的基本计算公式为:

式中 F——电磁吸力,J/cm
B——磁感应强度,Wb/cm2
S——磁极表面总面积,cm2
η——磁导率,此处代入25 ℃液态水的磁导率,为1.25×10-8H/cm
本文中电磁铁和衔铁均为圆环状,如图3 所示,根据该结构做出假设如下[2]:

图3 电磁铁和衔铁断面形状
(1)不考虑漏磁带来的影响。
(2)环形电磁铁安装轴不导磁,其磁导率按照空气磁导率计算。由此建立了磁路等效模型如图4 所示,得到磁通量计算式为:

图4 磁路等效模型

其中,IW 为线圈产生的磁动势;R1为铁心磁阻;R2为衔铁磁阻。
因为铁心及衔铁的磁导率相对空气磁导率要大很多,此时只考虑气隙磁导率的影响,即可以将式(2)简化为:

其中,G0为气隙磁导,计算式为:

由所建立的磁路等效模型,还可以得到电磁铁吸力计算公式为:

3 液膜压力的仿真计算和模型有效性验证
3.1 几何模型的建立
在动环低压侧开设N 个螺旋槽,动环端面呈中心对称,因此取做为计算区域,如图5 所示。在最终计算全周期液膜压力时,将单周期压力数值乘以N 即可得到结果。通过CeroE 建立端面密封模型,因为该模型的液膜部分在z 方向上的尺度为微米级,比x、y 方向上的尺度小很多,因此在随后的ICEM 中进行网格划分时,利用ICEM 自带的网格拉伸功能建立完整的液膜模型。

图5 单周期动环端面示意
几何参数和工况参数见表1。

表1 几何及工况参数
3.2 数学模型
假设润滑介质的流动是连续的且密度不变,当槽数趋向无穷多时,上述假设成立。根据窄槽理论[3],上述假设成立。进一步假设压力沿槽区和坝区呈线性分布,通过求解在槽区和坝区建立的微分方程,可以得到压力分布的表达式。
根据上述假设,在半径r 处取一宽为dr 的圆环,圆环上压力增量为dp,则对于泵出式螺旋槽,dp 与dr有如下关系式[4]:

式中 p——螺旋槽液膜压力
μ——黏度
ω——旋转角速度
h0——非槽区膜厚
h1——槽区膜厚,h1=h0+hg,hg为槽深
g1,g2——螺旋槽系数
γ——台槽比
q——泵送流量
H——非槽区膜厚与槽区膜厚比
α——螺旋线的螺旋角
将式(6)从螺旋槽内径到某端面位置进行积分,可得到槽区和坝区的压力表达式[5]:
槽区压力表达式:

坝区压力表达式:
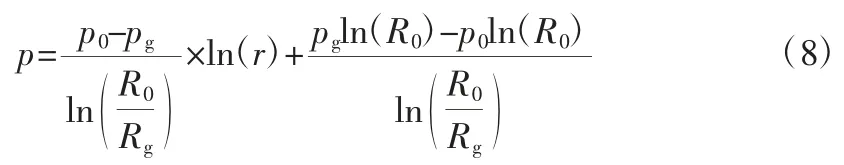
式中pg为槽坝交界处压力,计算式为:

式中 pi——密封环内侧介质压力
p0——密封环外侧介质压力
Ri——密封环内径
R0——密封环外径
Rg——密封环槽坝交界半径
3.3 网格划分及边界条件
采用Tri 三角形网格单元对垂直于z 轴的表面进行网格划分,而液膜在z 方向的网格由网格拉伸命令生成,如图6 所示。

图6 密封端面部分网格及液膜处的网格拉伸
螺旋槽内液体随着密封端面的旋转而运动,槽区使用Moving Reference Frame,然后设定转速,坝区其他设置保持默认。模型进出口端面分别采用压力进口和压力出口,其余两侧端面均采用interface[4],而槽区坝区交界处采用interior。
3.4 模型有效性验证
为验证本文算法的有效性,采用本文计算方法对文献[5]的研究对象进行计算,将计算结果同文献[5]的计算结果进行对比(表2)。取膜厚为1.5 μm,边界压力为0 MPa,介质为室温状态下的水。
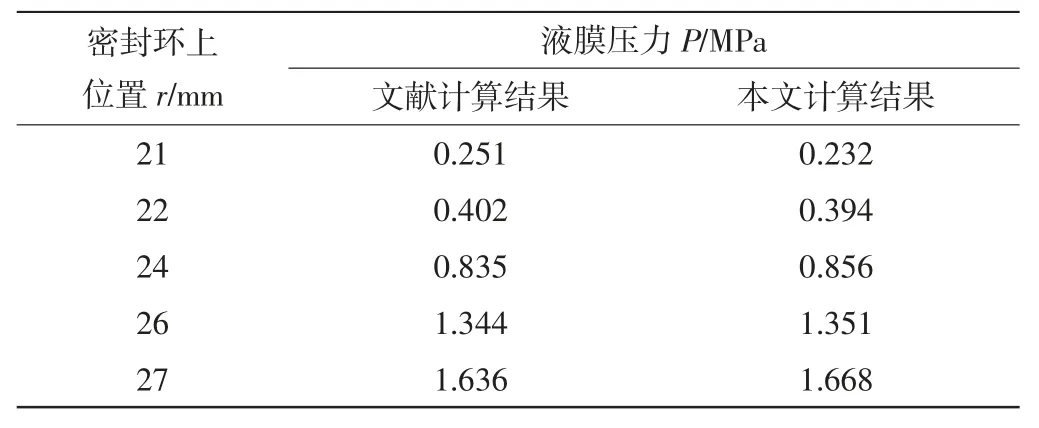
表2 计算结果与文献[5]结果对比
通过对比可以看出本文计算方法的计算结果与文献结果相近,且变化趋势一致,说明本文所使用的仿真方法具有较好的可靠性。槽区润滑膜压力计算结果如图7 所示。

图7 槽区液膜压力云图
4 间隙主动控制分析
4.1 控制方程的建立
对图2 中的静环进行受力分析,静环受液膜压力、弹簧弹力、大气压力和电磁力的影响。控制方程是在静环受力平衡为基础的条件下得出的,即:

将各项表达式代入得:

式中,k 为弹性系数,Δx0为装置未工作时弹簧的初始形变量,S 为静环周向面积,δ 为液膜厚度。
4.2 控制系统有效性分析
为了确定控制系统的有效性,引入敏感性参数作为判断指标δ[6]。敏感性参数δ 的定义为:

式中,α 为控制量的权重参数,本文认为摩擦力矩与温度权重相当,即α 取0.5;K*表示可控型密封在静态平衡位置时的阈值;Ki表示可控型密封在时刻i 时的阈值;Nfi和Ti分别表示摩擦力矩、温度在时刻i 的值和T*分别表示摩擦力矩、温度在静态平衡时的值。根据张国渊等的研究[6],利用电磁加载装置进行主动控制的密封系统的敏感性参数的一般取值范围为1≤δ≤3.19。在转速变化的情况下,的值选取其在三种特定转速(1500 r/min、5000 r/min、10 000 r/min)下的最大值[7],即1.9、1.1。代入式(12)得到所需的敏感性参数最大值为1.5,小于3.19,说明本文研究的密封系统可以达到主动控制的目的。
5 结论
本文提出非接触式静止式机械密封间隙主动控制的方法,设计相应的控制系统,能够实现密封间隙的有效控制且辅助控制元件不受密封介质的影响,同时,该方法及系统对于类似的间隙控制具有一定的参考价值。建立密封间隙主动控制的数学模型,结合工况变化分析,说明控制系统的有效性。

