基于身份的可审计多重截取签名方案*

何启芝，曹素珍，王彩芬,2，卢彦霏，方子旋，闫俊鉴

(1.西北师范大学计算机科学与工程学院，甘肃 兰州 730070；2.深圳技术大学大数据与互联网学院，广东 深圳 518118)

1 引言

传统数字签名技术可以保证数据在传输过程中的完整性和不可抵赖性。然而，在一些特定的应用环境中，传统数字签名技术并不能完全满足安全需求。如图1所示，总公司文件处理部门签署一份重要的电子文件后，为最大程度地减少对公司敏感信息的泄露，要求各子公司文件处理者根据工作需要截取一部分内容并转发给下属各部门，各部门能在不与总公司文件处理者交互的情况下，确认收到的文件是合法有效的。

Figure 1 Example of an application scenario 图1 应用场景实例

为满足上述应用环境对签名文件的安全要求，必须对传统签名根据特定规则按需截取，确保截取后的签名合法有效且不存在二义性。内容可截取签名CES(Content Extraction Signature)[1]的提出解决了上述问题，且能保证各公司、各部门收到的文件是不可伪造的，同时保证总公司可以完全控制对原文件的截取方式。

具有可删改性质的内容可截取签名CES于2001年由Steinfeld等人提出，内容可截取签名允许用户根据需要，在不与原始签名人交互的情况下，对已签名数据进行截取，并且得到一个可验证的截取签名，实现了保护数据隐私的功能。蓝才会等人[2]在2007年提出了一个基于身份的内容可截取签名方案，该方案结合了可截取签名体制和批签名的思想，不需要对消息的每个子消息进行签名，但是由于该方案使用了双线性对技术，因此整个方案的效率比较低。曹素珍等人[3]在2013年提出了一个基于离散对数DLP(Discrete Logarithm Problem)[4]问题的内容可截取签名方案，进一步提高了计算效率。但是，文献[2，3]不能实现对签名的可审计性，不支持对数据发布者和签名者身份的追溯，不能解决恶意修订(即不按照修订控制规则修订或截取)的问题。2002年Johnson等人[5]提出的可修订签名方案RSS(Redactable Signature Scheme)是具有同态性质的数字签名，可实现修订人不与签名人交互就能删除已签名消息的部分数据，同时为修订后的消息生成新的签名，并能验证该签名是具有同态性质的签名，具有很广阔的应用前景，但是仍无法解决恶意修订问题。2015年Pohls等人[6]提出了一个可审计的可修订签名ARS(Accountable Redactable Signature)方案，该方案解决了当出现数据责任纠纷时，允许一个任意的仲裁第三方针对纠纷数据的签名是否有效来判定责任，且该签名人无法抵赖责任。2020年，马金花等人[7]提出了一个公开可审计的可修订签名方案的通用框架，该框架可以利用传统的数字签名方案将任意的可修订签名方案转化为公开可审计的可修订签名方案，从而实现签名人和修订人的公开可审计性。与文献[6]中的方案相比，该方案更适用于对开放环境中的数据进行修订，并且计算开销更小。当数据内容产生纠纷时，由于该方案只能证明数据的来源(来自签名者或修订者)，并不能有效阻止恶意修订情况的发生，因此其可用性并不强。

多重签名[8]可以实现多个人对同一个消息分别进行签名。根据签名有无顺序，多重签名分为有序多重签名[9]和广播多重签名。Wu等人[10]提出了基于身份的多重签名方案，随着多重签名的不断发展，研究人员已经基于多重签名的安全性、机密性和实用性提出了许多扩展应用方案[11 - 14]。此后，Gentry等人[15]提出了一个基于Weil 对的基于身份的广播多重签名方案，该方案基于计算DH CDH(Computational Diffie-Hellman) 困难问题[16]，并证明了在随机预言模型下是安全的。

鉴于此，本文在文献[2]的基础上借鉴多重签名的思想，提出了一个基于身份的可审计多重截取签名方案。方案首先构造了一个M叉树模型，通过该模型来实现广播多重签名，即从根节点向子节点实现分层广播签名。由于层级划分明确，当出现纠纷时可从下往上进行逆向追踪，从而实现对截取签名的可审计性，保证签名的合法性。其次，在随机预言模型下，基于离散对数困难问题证明了方案可抵抗适应性选择消息攻击下的存在性伪造。与文献[2，3]中的方案相比，本文构造的可截取签名方案具有更高的签名效率。

2 预备知识

2.1 符号说明

本文方案中使用的部分符号说明如表1所示。

Table 1 Symbol description表1 符号说明

假设一个消息m由n个更小的子消息组成，即m={m1,m2,…,mn}。截取的子消息可表示为m′={m′1,m′2,…,m′n}，CI(m′)是由m′中所包含的子消息段的编号构成的集合。消息m根据CI(m′)所指定的m′进行截取。CEAS是内容截取访问结构，签名者通过CEAS来构造截取子集CI(m′)，用来指定提取哪些子消息的有效签名。

2.2 相关困难问题

设群G是阶为q的乘法循环群，G的生成元为g。

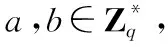
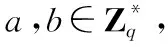
2.3 内容可截取签名

内容可截取签名过程由如下4个核心算法构成：

(1)密钥生成。输入系统安全参数λ，生成一个公/私钥对(pk,sk)；

(2)签名。该算法由签名者运行，输入签名者私钥sk、内容截取访问结构CEAS和签名数据m，输出一个数据/签名对(m,σ)。

(3)截取签名。该算法由截取者运行，输入签名者公钥pk、截取者私钥sk、截取子集CI(m′)和数据/签名对(m,σ)，输出截取后的数据m′和截取签名(m′,σ′)。

(4)验证签名。输入签名者公钥pk、截取后的数据m′和截取签名(m′,σ′)，若签名有效，输出True；否则，签名无效，输出False。

假如原始消息是m={m1,m2,m3}，截取子集CI(m′)={1,3}，则对应的截取子消息是m′={m1,?,m3}，用“？”表示没有被截取的子消息段。需要注意的是，根据m′的定义，截取子集和截取的子消息段要一一对应，其顺序也要和原消息中的子消息段顺序保持一致，如截取子集CI(m′)={1,3}，则截取子消息m′={m1,m2,?}是非法的，因为截取子消息没有和截取子集CI(m′)对应起来；截取子消息{?,m1,m3}和{m1,m3,?}也都是非法的，因为没有与原消息中的顺序保持一一对应。

3 方案描述

3.1 形式化定义

可截取签名方案主要包括签名者、截取者和验证者，而且截取者和验证者可以是同一人，签名者完成对原始消息的全局签名，截取者首先完成对消息正确性的验证，接着完成对消息的截取签名。该方案由以下5个算法构成：

(1)系统建立Setup(λ)。

选取一个安全参数λ，PKG生成系统主密钥和系统参数par，保密主密钥，将系统参数公开。

(2)密钥生成KeyGen(par)。

输入安全参数k，为签名者生成一个公/私钥对(pk,sk)。

(3)签名生成Sign(sk,m,CEAS)。

签名者为根节点生成签名(普通签名)，输入签名者的私钥sk、消息m、内容截取访问结构CEAS，输出一个可截取的全局签名(m,σF)。

(4)截取签名生成Extract(pk,(m,σ),CI(m′))。

①首先验证上一级的签名是否有效，若签名有效，继续执行下面的算法；否则，终止算法。

②输入签名人的公钥pk、签名(m,σ)和截取子集CI(m′)，该算法输出截取后的签名(m′,σE)。

(5)验证Verify(pk,m′,σE)。

输入m′,σE,pk验证整个签名，若通过验证，表示截取签名有效；否则，截取签名无效。

3.2 安全模型

引理1若存在敌手F在概率多项式时间内赢得以下游戏的优势是可忽略的，则称本文所提的可审计多重可截取签名方案在适应性选择消息攻击下满足不可伪造性。

证明挑战者C和敌手F之间的交互游戏定义如下：

(1)初始阶段(Setup)。挑战者C执行密钥生成算法，生成公/私钥对(pk,sk)，然后将公钥pk发送给敌手F，保密私钥sk。

(2)询问(Qureies)。敌手F能够向挑战者C自适应地进行一系列不同的询问，具体如下：

①密钥提取询问。敌手F能获取任何身份u所对应的私钥，挑战者C执行密钥生成算法，输出身份u所对应的私钥Su并返回给F。

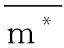
③H2询问。假设mi是m的子消息，F向C发出H2询问，C运行Sign算法，计算H2(mi‖CEAS)发送给F。

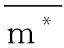
‖H2(m3‖CEAS)‖…‖H2(mi‖CEAS))

发送给F。

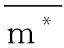
⑥签名询问。假设mi是m的子消息，F向C发出签名询问，C运行Sign算法，计算σi并返回给F，F最后构造出原消息的全局签名σF。

⑦签名截取询问。F收到消息m的全局签名σF后，根据C发送的CEAS构造出CI(m′)，C运行Extract算法，计算消息m截取后的子消息m′的签名σ′并验证该签名是否有效。

(3)伪造(Forgery)。经过多项式次询问后，敌手F输出伪造身份u*对消息m*的截取签名σ*，并使以下3个条件成立，则说明攻击成功：

①敌手F没有发起过对身份u*的密钥提取询问；

②敌手F没有发起过对(u*,m*)的签名询问；

③通过验证算法可以验证σ*是身份u*对于消息m*的有效签名。

定义1如果敌手F的运行时间最多为t，密钥提取询问最多发起qe次，H1询问最多发起qH1次，H2询问最多发起qH2次，H3询问最多发起qH3次，H4询问最多发起qH4次，签名询问最多发起qs次，签名截取询问最多发起qSE次，以不小于ε的概率赢得上述游戏，则称敌手F是基于身份的可截取签名方案的(t,ε,qe,qH1,qH2,qH3,qH4,qs,qSE)-伪造者。如果在该方案中不存在(t,ε,qe,qH1,qH2,qH3,qH4,qs,qSE)-伪造者，则称方案是(t,ε,qe,qH1,qH2,qH3,qH4,qs,qSE)-安全的。

3.3 方案构造

本文方案需要构建一棵M叉树，具体构建方法如图2所示。

Figure 2 M-tree model图2 M叉树模型

从图2可以看出，M叉树在根节点处进行原始签名，分支节点(虚线框中的节点)在图中只表示出了1层，但是在具体方案中可能有很多层。第2层虚线框的内部线条是虚线，表示分支节点可以有很多层。

根据图2所示的模型构建M叉树的方法，遵从树形结构中从根节点到叶子节点的顺序，整个过程是一个分级广播多重签名的过程。首先在根节点处，将该签名分成若干子消息后进行根签名；在第2层，首先进行判断，根据内容截取访问结构CEAS判断每个子消息是否需要进行截取签名，若需要进行截取签名，则继续同样的步骤。在每一层，分别进行广播多重签名，即不分签名的先后顺序分别进行截取签名，这样便得到了一棵M叉树，同时还实现了分级广播多重签名。构建M叉树的算法如算法1所示：

算法1构建M叉树

输入：消息m，CEAS。

输出：一棵M叉树。

步骤1Getm={m1,m2,…,mn}fromthesigner；

步骤2ComputeσF={m,CEAS}；

rootNode←σF；

步骤3 fori=1 tondo

Computeσmi=(mi,CEAS)；

endfor

步骤4 ifmi+1∈CI(m′)then

childNodemi←σmi+1；

else

siblingmi←σmi+1；

endif

方案具体构造如下：

(1)Setup(λ)。

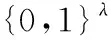
(2)KeyGen(par)。

假设ID表示签名者的唯一可识别的身份，PKG对签名者进行鉴定，确信ID具有唯一性。

②PKG计算QID=H1(ID)作为签名者的公钥，任何人都可通过系统的公开参数计算得到签名者的公钥。

③PKG计算SID=sQID，将它作为签名者的私钥并安全地发送给签名者。

(3)Sign(sk,m,CEAS)。

假设被签名的消息为m，根据需要m被划分为x个部分，mk表示m中的子消息段，k为子消息段在消息m中的编号，k∈{1,2,…,n}，m′表示截取后的子消息。

假如m={m1,m2,m3}，则

H2(m3‖CEAS))

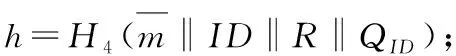
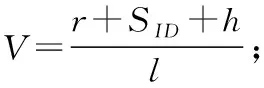
(4)Extract(pk,(m,σ),CI(m′))。

①根据CEAS构造CI(m′)；

②用m′={m′1,m′2,…,m′n}代替m={m1,m2,…,mn}:

(5)Verify(pk,m′,σE)。

①判断者首先验证CI(m′)∈CEAS是否成立，若成立，则继续；否则，终止算法；

4 方案分析

4.1 正确性分析

在截取签名算法中，替换各子消息段的方法如式(1)所示：

(1)

(2)

从式(1)和式(2)可以得知，验证时每个子消息段和签名中的子消息段是一致的，均为H2(mi‖CEAS)。

本文方案具有可审计性，可以追踪到恶意修订的敌手。由于分支节点需要先验证签名，再截取签名，因此审计和追踪是在父节点与子节点之间完成的。构造的一个攻击场景模型图如图3所示，F为敌手，其子节点A既是节点F的签名验证者同时也是截取签名者，若A未能通过截取签名验证，则A还可作为一名审计者进行逆向追溯(如图3中虚线框所示)，且将追溯结果反馈至敌手的父节点，从而追踪到敌手F，以便制止敌手F的恶意修订行为。

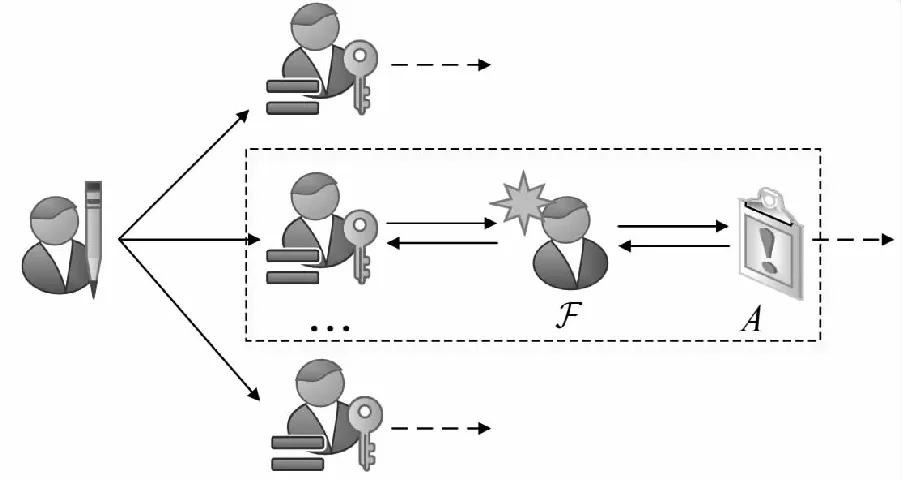
Figure 3 Model of attack scenario图3 攻击场景模型图

由以上分析得知，本文方案是正确的。

4.2 安全性证明

挑战者C还有一个身份，就是DLP问题的攻击者。假定已知(g,b=ga)，要求挑战者C计算出a的值。

定理1在随机预言模型下，若存在一个敌手F能够以不可忽略的优势在概率多项式时间内赢得引理1中的游戏，则挑战者C就能够以一定的优势解出离散对数困难问题。

证明挑战者C运行系统建立算法，设b=ga，然后生成系统公开参数par={G1,G2,g,b,q,H1,H2,H3,H4}，并将系统公开参数发送给敌手F，挑战者C与敌手F执行以下模拟算法。

敌手F选择一个身份ID，能够模仿一般用户进行自适应地询问，密钥提取询问最多发起qe次，H1询问最多发起qH1次，H2询问最多发起qH2次，H3询问最多发起qH3次，H4询问最多发起qH4次，签名询问最多发起qs次，签名截取询问最多发起qSE次，询问如下：

(1)密钥提取询问：挑战者C维护初始值为空的表Lk，表中记录(ID,QID,SID,R)，敌手F询问身份IDu的密钥，挑战者C执行以下操作：

①若表Lk中存在ID对应的四元组，则将所对应的值返回给敌手F；

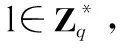
(2)H1询问：挑战者C维护初始值为空的二元组列表L1，表中记录(ID,QID)，敌手F询问，挑战者C执行以下操作：

①若表L1中存在ID对应的二元组，则将所对应的值返回给敌手F；

②若表L1中不存在ID对应的二元组，则计算QID=H1(ID)，将其加入列表L1中并返回给敌手F；

(3)H2询问：挑战者C维护初始值为空的二元组列表L2，表中记录(mi,CEAS)，敌手F询问，挑战者C执行以下操作：

①若表L2中存在IDi对应的二元组，则将所对应的值返回给敌手F；

②若表L2中不存在IDi对应的二元组，则计算H2(mi‖CEAS)，将其加入列表L2中并返回给敌手F；

①若表L3中存在IDi对应的三元组，则将所对应的值返回给敌手F；

H2(m3‖CEAS)‖…‖H2(mi‖CEAS))，将其加入列表L3中并返回给敌手F；

①若表L4中存在IDi对应的三元组，则将所对应的值返回给敌手F；

(6)签名询问：挑战者C维护初始值为空的四元组列表Ls，表中记录(ID,m,CEAS,σ)，敌手F询问，挑战者C执行以下操作：

①若表Ls中存在ID对应的四元组，则将所对应的值返回给敌手F；

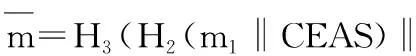
(7)签名截取询问：挑战者C维护初始值为空的四元组列表Lr，表中记录(ID,m′,CEAS,σ′)，敌手F询问，挑战者C执行以下操作：

①若表Lr中存在ID对应的四元组，则将所对应的值返回给敌手F；

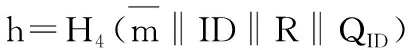
由上述分析可得，本文基于身份的可审计多重截取签名方案在适应性选择消息攻击下具有不可伪造性。

4.3 性能分析

本节将文献[2,3]方案与本文方案的计算效率进行比较。常用的密码操作有par、exp和has，其中，par表示双线性对运算，exp表示指数运算，has表示哈希运算。文献[2，3]中的方案与本文方案所采用的运算次数如表2所示。

Table 2 Number of different operations used in the scheme 表2 方案采用的不同运算次数

如表2所示，文献[2]方案在签名和验证阶段都采用了双线性对运算，文献[3]方案采用的指数运算也要多于本文方案的，实验运行环境是Intel(R) Core(TM) i5-7200U CPU@2.50 GHz处理器、12 GB内存、Windows 10操作系统，基于JPBC(Java Pairing-Based Cryptography)库用Java语言实现。通过实验可以得到不同方案的运算时间，如表3所示。

Table 3 Computing time of different schemes表3 不同方案的运算时间 ms

为了更直观地展现本文方案在计算效率方面的优势，文献[2,3]方案和本文方案的实验结果如图4和图5所示。

Figure 4 Computational overhead of signature and extraction phases图4 签名及截取阶段的计算开销

Figure 5 Computational overhead of signature verification phase图5 验证签名阶段的计算开销

图4是在签名及截取阶段对不同方案进行比较，随着截取子消息的不断增加，3个方案的运算时间也在不断增加，由于文献[2]方案在该阶段采用了双线性对运算，因此该方案的计算开销最大，文献[3]方案在该阶段未采用双线性对技术，但是由于指数运算较多，计算开销也高于本文方案的，可以看出本文方案的计算开销优于文献[2，3]方案的。在验证签名阶段，由于文献[2]方案在该阶段采用了双线性对运算，导致该方案的计算开销明显高于文献[3]方案和本文方案的，虽然本文方案和文献[3]方案的计算开销差别不是很大，但是随着验证签名中截取子消息的增加，本文方案的计算开销始终低于文献[3]方案的计算开销。

由以上分析可以得出，在签名及截取阶段和验证签名阶段，本文方案的计算开销都要比文献[2,3]方案的计算开销小。

5 结束语

本文提出的可审计多重截取签名方案，利用M叉树模型实现了多重截取签名，通过对M叉树中节点的逆向追溯，可实现对恶意修订者的审计追踪。实验结果表明，本文方案没有采用对运算，仅采用了少量指数运算和哈希运算，与同类签名方案相比，计算成本降低了很多，更适用于电子商务、电子政务及网络电子投票等应用场景。下一步考虑如何实现不同需求下的消息截取，然后将特定的截取消息发送给相应的验证者，实现签名的多样性。