家具产品抽样特性曲线的下降弧指标性能评价*

赵嘉琪 蒋南云 樊树海

（1.南京工业大学工业工程系，江苏 南京 210009；2.麻省理工学院信息质量项目数据质量与信息安全实验室，美国 马萨诸塞州 02139）

我国家具制造与销售行业自20世纪80年代开始，经过近40年的蓬勃发展，至2021年，据中国家具协会发布的全年家具行业运行概况报告显示：2021年全年家具行业营收累计8 004.60亿元，累计产量11.2亿件[1]，我国已成为家具制造与出口大国。对于家具制造业而言，家具企业诚信建设根基在于产品质量[2]。在行业内同等的高质量水平下，降低企业的质量成本，是提升企业盈利水平的重要途径[3]。在质量成本中，检验成本的占比不容忽视。制造企业对大批量生产的产品进行质量检验时，为减少工作量与检验时产生的产品与资源的损耗，通常会采取抽样检验的方式[4]。

近年来，国内外学者为提升质量绩效、降低产品检验成本，针对抽样方法与方案的制定问题进行了大量研究。Razmkhah等[5]提出采用最大提名抽样法（maxima nomination sampling）抽样，以达到样本选取量小且成本更低的目的。Lindsay[6]为质检时预估每种产品需要检查的次数及会预估出现检验错误的比例提供了方法。Tamirat等[7]提出了兼具灵活性和经济性特点的抽样方法——基于EWMA的抽样计划。Chen等[8]则提出了在生产者风险、客户风险和工艺能力指标三个条件的约束下，以最大化产品批次的期望总利润来确定抽样方案参数的方法。Dodge-Romig[9]提出利用通过变量和属性进行检验的平均出厂不合格品率上限（AOQL）计划假设，使检验成本最小。

在现实的产品检验工作中，为了使抽样方案参数的确定更加准确高效，生产方普遍会采用对比抽样方案的抽样特性曲线（Operation Characteristic Curve，简称OC曲线）的方式来比较各个方案的鉴别能力[10]。以往生产方分析OC曲线的常用方法是对比由众多抽样方案所生成的OC曲线族，凭经验通过OC曲线的形状判断OC曲线的优劣。

本研究的目标主要为以下4 点：1）改变仅凭经验对比OC曲线族来筛选家具产品的抽样方案，这种直观定性的对比方法；2）突破传统方法中对比抽样方案时只能变动方案单参数对比的局限；3）能够快速而又灵敏地判断家具产品抽检批的质量是否合格；4）在检验时能够使抽样次数和抽检样本量都尽可能地少，从而达到降低家具产品检测成本的目的[11]。

鉴于此，本文提出一种可行的基于下降弧的抽样特性曲线评价指标，利用该评价指标不仅可打破以往单凭经验来判定抽样方案优劣的弊端、提高定量度量抽样特性的灵敏度，且操作更为便捷、计算更为快速、成本更为低廉。此外，该指标还可与家具产品生产过程中的接收质量限（AQL）等其他质量指标相结合，实现对产品抽样方案的多变量联合定量评价，达到提高质量绩效与降低检验成本的目的。

1 质量成本管理

质量管理以建立一个高质量的产品或服务，满足并超过顾客的期望为目的[12]。产品及服务质量是市场成功的重要决定因素，也是竞争的基本要求[13]。质量对于家具企业而言是可持续发展的源动力[14]，通过质量管理可以提高组织效率和竞争优势[15]。美国学者菲根堡姆提出把企业生产时在质量方面所耗费的预防成本、检验成本与产品质量不过关所产生的损失结合在一起考虑，即考虑“质量成本”[16]。国内的家具行业已经具有较大的规模，但是具有较强质量成本管控能力的企业为数不多，且品牌影响力强的企业较少。成本是家具企业创造经济价值的基础[14]。所以，同等质量水平下，想要在市场竞争中提升企业的盈利能力，有效的方法之一就是降低企业的质量成本[3]。

质量成本包括预防成本、检测成本、内部故障成本和外部故障成本[17]。其中，检测成本通常会维持在10%～50%[18]。根据对某制造型企业2017年全年的质量成本的数据统计，可知在总质量成本中，检测成本占比27.91%，仅次于占比29.51%的内部损失成本[19]。检测成本在制造业中通常占总质量成本的1/4及以上。因此，检测成本的降低，将有效降低质量成本，提升盈利水平。

2 OC曲线分析

在抽样检验时，合理确定样本容量和有关接收准则的一组规则称为抽样方案[20]。（N,n,c）即表示一组抽样方案，其含义为从一批总体批量为N的产品中，抽检数量为n的一批样本，该批抽检样本如果满足判定标准c，则判定该批产品合格，否则判定该批产品不合格。对于抽样方案的合理程度的判断，主要依据对OC曲线的分析与对比。OC曲线表示在给定的抽样方案中，批接收概率L(p)与批不合格品率p的函数关系[21]。

典型的抽样特性曲线如图1中所示，接收概率L(p)随不合格品率p的升高而单调下降；理想的抽样特性曲线，呈图2所示的方波状，其表示在产品质量好时将被完全接收。L(p)保持为1，质量差时则完全不接收，L(p)为0，并且中间几乎无过渡部分。然而在实际生产与检验中，这种理想OC曲线是不现实也不存在的[22]。

图1 典型抽样特性曲线Fig.1 Typical sampling characteristic curve

图2 理想抽样特性Fig.2 Ideal sampling characteristics

抽样检测以能用较低的检测成本，快速精准地判断出产品质量是否达标为目标，因而要求抽样方案具有较高的灵敏度[23]。判断抽样方案是否灵敏，要看该方案能否精准地把一批质量较好的产品以高概率判定为合格，又能否把一批质量较差的产品以高概率判定为不合格，反映在OC曲线中即可以表示为接收情况不确定性高的中间过渡部分较少[20]。

以往生产方分析在OC曲线时，常用的方法及步骤如下：

1）固定其余参数，依次变动抽样方案的单参数；

2）其次根据单参数值的变化及其对应的固定参数值，生成相应的OC曲线族；

3）直接凭经验在图像中对各曲线进行直观定性地比较，从而确定抽样方案的优劣[24]。

该种方法的弊端在于对曲线族的对比与选取主要是依赖质量管理人员的经验判断，缺少准确严谨的定量分析方法。研究者提出了基于信息熵、基于截距的OC曲线评价指标，使定量分析抽样特性曲线成为可能[20，25]。

3 下降弧评价指标

OC曲线两端点的接收概率分别为0、1，代表一定不接收或一定接收，意味着这两点抽样方案“接收事件”的不确定性最小；当接收概率为0.5时，“接收事件”的不确定性最大，最难判断是否会被接收[20]。抽样方案的不确定程度越低，方案的灵敏度和准确度越高，反映在抽样特性曲线图中，可表现为OC曲线中部代表着不确定性高的部分较少[26]。据此，本文提出了基于下降弧的OC曲线性能评价指标。

以下降弧为评价指标的OC曲线判别法步骤如下：

1） 给定两个不同水平的接收概率La、Lb，La取0.7，Lb取0.3；

2） 在OC曲线图中标出La、Lb两点，过La与Lb同时作平行于x轴的虚线，分别与OC曲线交于a、b两点；

3） 连接a与b点作一条直线，接着再分别过a、b两点作平行于y轴的虚线，交x轴于Pa、Pb两点，此两点分别代表质量较好时与质量较差时的不合格品率。

为更好地展现指标的规律性，使后续的计算及仿真结果将指标的变化情况展示得更加直观，取直线与x轴正半轴夹角的补角θ，用θ的弧度值大小情况，来评价抽样方案的优劣，如图3所示。

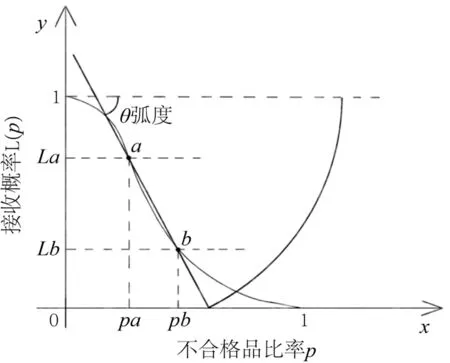
图3 下降弧判别法Fig. 3 Descent arc discrimination

根据弧度计算公式及a、b点数据，得到下降弧评价指标：

式中：La为a点的接收概率；Lb为b点的接收概率；pb为b点的不合格品率；pa为a点的不合格品率。

在本文中，代表OC曲线不确定性较大的中间段部分定义为：在OC曲线上分别取接收概率为0.7与0.3的a、b两点，这两点间的OC曲线段即为该OC曲线的中间段部分（必须保证OC曲线上接收概率为0.5的点包含在ab段内）。a、b两点投影到横坐标轴落在Pa、Pb两点，通过计算线段PaPb的长度占横坐标轴不合格品率为0～1范围内的比例，可以衡量中间段在整条OC曲线的占比。对OC曲线图及下降弧指标公式进行联合分析可以得出，下降弧指标值越小，OC曲线中不确定性大的中间段占比越多，方案的不确定性程度高；下降弧指标值越大，OC曲线的中间段占比越少，方案的不确定性程度低，曲线越接近理想情况。综上所述，抽样方案的下降弧指标值越大，该方案的灵敏度与准确性越高，该抽样方案性能越好。

4 仿真与实现

4.1 仿真实验验证可行性

在仿真实验中有：

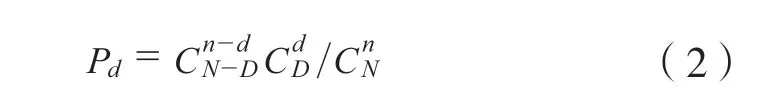
式中：Pd为从总体批量为N且包含D个不合格品的被检批中，随机抽取大小为n的样本，在样本中检出d个不合格品的概率；n为抽取的样本量，pcs；d为样本中的不合格品数量，pcs；N为该批被抽检批的总量，pcs；D为被检批的不合格品总量，pcs；注：c≤n≤N,D应取整数。

在抽样确定为计数一次型，且抽样方案参数已确定时，根据加法定理计算接收概率有：

又有下降弧评价指标：

在N确定的情况下，每输入一组抽样方案(N,n,c)，经下降弧评价指标的一系列运算都会有一个下降弧指标值R(N,n,c)与之相对应。

为验证指标的可行性，使用Matlab软件对下降弧评价指标进行仿真实验。指标仿真实验的流程如图4所示，具体流程如下：

图4 仿真流程示意图Fig.4 Schematic diagram of simulation flow

1）初始化，输入固定参数N、La、Lb等（N设为50）；

2）输入(n,c)值；

3）调用下降弧计算模块计算R(N,n,c)；

4）调用计算接收概率L(p)模块；

5）根据参数类型，在三种分布模块中选择性调用，算出不合格率Pd；

6）返回2)输入其他需要仿真的参数值；

7）汇总并作图。

仿真实验生成的三维图像如下：

如图5所示，样本数轴代表样本空间n，判定标准轴代表接收判断标准c，下降弧轴代表下降弧指标Rad。在N设定为50的情况下，输入一组抽样方案(N,n,c)，经一系列计算都会有一个抽样特性曲线的下降弧评价指标值R(N,n,c)与输入的方案参数相对应。R、n、c三项数据对应，则构成如图5的三维空间曲面图。

图5 下降弧指标三维图仿真结果Fig.5 The simulation results of the three-dimensional graph of the descending arc index

仿真三维图中显示，在n＞c的情况下，c越小，或者n越大，指标R的值会呈现增长趋势，意味着抽样方案的不确定性在降低。表明选取的抽样方案越严格，检验时对产品的把关与筛选越苛刻，企业耗费的代价也就越大；相反，c越大，或者n越小，下降弧指标R值变大，表示系统的不确定程度增高，抽样方案越松弛，不合格品流出的可能性越大。三维图中n≤c的区域，表示在该批产品质量不符合出厂标准时，检验时仍然判定接收，那么该区域无实际意义，不予考虑。

4.2 实例演示

有一批总量为50 的被检批产品，在对该批产品进行抽样检验前，有备选的四个抽样方案，如表1 所示。利用OC曲线的下降弧评价指标对以上四个抽样方案进行运算与仿真，对比出各方案的优劣，从而选取出最佳抽样方案。

表1 备选抽样方案Tab.1 Alternative sampling scheme

1）利用MATLAB软件打开编写完成的下降弧指标运算与仿真程序，点击运行后的操作提示界面：

界面引导用户根据提示输入抽样方案的参数。在命令框中按照该提示依次输入备选抽样方案的三个参数值N=50、n=8、c=3。每输入一个参数均以Enter键结束。

2）抽样方案的参数输入完毕后键入Enter键，即可输出抽样方案数据及该抽样方案的下降弧指标值：

3）分别输入4 个备选抽样方案的参数值，程序依次运行后，得到的下降弧指标参数值如表2 所示。

表2 试验参数及结果Tab.2 Test parameters and results

对比表格中的数据可知，抽样方案3的下降弧指标值最大，为2.890 5；抽样方案2的下降弧指标值最小，为2.036 5。根据抽样特性曲线的下降弧指标的理论及评判方法，下降弧指标参数值越大，方案的不确定性程度越低，曲线越接近理想情况。在4个方案中，抽样方案3的不确定性程度最低，该方案用于检验时的准确性和灵敏度相对较高，所以应选取方案3作为最终的抽样方案。

5 结论

仿真实验的结果证明了“基于下降弧指标的抽样特性曲线性能评价方法”是可行且有效的。该指标的运用将以往直接依靠经验对比与选取OC曲线的方法，优化为利用下降弧指标值对OC曲线进行科学量化的对比，使定量度量抽样特性曲线成为可能，提高了度量的灵敏度，且进一步丰富了评价抽样特性曲线时可供选取的指标。

该指标在运用时操作更为便捷，能够做到低成本、快速地对多个抽样方案进行对比与选取，使抽样方案之间的对比通过数据与表格得到更加直观地展现。在尽可能降低抽样次数和抽检样本量，减少家具产品因质检损坏造成损失的情况下，快速灵敏地对抽检样本判断质量是否合格。家具制造企业在质量检验时，将接收质量限（AQL）与以该指标为依据制定的抽样方案综合考虑，制定出抽样计划，再与统计过程控制的方法相结合，可明显提升质量绩效[8]，实现将抽样方案进行多变量的联合评价的可能。

产品检测成本的有效控制，使质量成本得到了一定程度的降低，这在竞争激烈的市场中，将是家具制造企业提高盈利水平、提升企业竞争力的重要途径。