例谈玻尔原子理论中的量子化条件与应用

许冬保

(江西省九江第一中学 332000)

1 玻尔原子理论基本假设

玻尔理论是继普朗克量子假说和爱因斯坦光子理论之后，向微观研究领域跨出的重要一步，开创了原子现象研究的先河.玻尔理论中轨道量子化条件表明，普朗克常量在原子现象中起着十分重要的作用，它不仅决定了原子的大小、原子的能级结构，同时它也能很好地说明氢原子光谱.

1.1 现行高中教材的表述

在人教版物理教材中，在“氢原子光谱和玻尔的原子模型”一节中，介绍了玻尔原子理论的基本假设，其内容要点包括2方面内容，即：

(1)轨道量子化与定态：玻尔认为，原子中的电子在库仑力的作用下，绕原子核做圆周运动……；电子运行的轨道半径不是任意的，只有当半径的大小符合一定条件，这样的轨道才是可能的.也就是说电子的轨道是量子化的.

(2)频率条件：当电子从能量较高的定态轨道(其能量记为En)跃迁到能量较低的定态轨道(能量记为Em，)时，会放出能量为hν的光子(h是普朗克常量)，这个光子的能量由前后两个能级的能量差决定，即hν=En-Em.

1.2 玻尔氢原子量子化条件

现行教材中，玻尔提到的轨道量子化，仅仅局限在文字描述的层面，未给出定量的表达式，存在明显的缺陷，由此带来学生知识结构的断裂.玻尔量子化条件表述如下：

考察氢原子，若核外电子的质量为m，在半径为r的圆周轨道上以速率v运动；普朗克常量为h，约化普朗克常量为ћ，则有

上式为玻尔量子化条件的数学表达式，n为量子数.

表达式中的“mv·r”是动量与半径的乘积，为电子运动的角动量大小.

2 应用分析

补充了氢原子轨道量子化条件，完善了玻尔氢原子模型的认知结构，对于有关问题的分析便不再存在困惑.

2.1 玻尔轨道量子化条件与德布罗意波长之间的关系

例1 德布罗意指出：玻尔模型与电子的德布罗意波长之间存在着一个很有意思的关系，叙述并推导这个关系.

解析德布罗意认为，实物粒子也具有波动性，与实物粒子相联系的波称为德布罗意波或物质波.德布罗意发现，玻尔提出氢原子中电子的圆轨道模型，刚好能容纳整数个电子的德布罗意波长，否则氢原子便是不稳定的.

设电子的德布罗意波长为λ，如上所述，对于氢原子核外电子，玻尔轨道量子化条件，表述为

2πr=nλ(n=1，2，3…)

该式的物理意义是：电子绕核运动周长等于其德布罗意波长的整数倍.

评述在历史上，玻尔1913年提出氢原子理论.1924年德布罗意提出物质波的概念，至此，玻尔轨道量子化条件才具有较直观的物理意义.

2.2 玻尔氢原子模型

例2设无限远处氢原子体系的电势能为零，已知电子电荷量为e，质量为m，普朗克常量为h，静电力常量为k，试求量子数为n时：

(1)核外电子轨道半径的表达式；

(2)氢原子处于基态时的电离能.

评述在推导氢原子核外电子轨道半径及氢原子能级的过程中，依照经典电磁理论、牛顿运动定律及轨道量子化条件建立方程，其中，玻尔轨道量子化条件是量子论思想的表现，也是玻尔氢原子理论精髓之处.氢原子能级表达式也可由巴耳末公式导出.过程如下：

2.3 玻尔类氢离子模型

例3已知电子电荷量为e，质量为m，普朗克常量为h，静电力常量为h.根据玻尔原子模型导出He+的能量表达式.

解析设电子电荷量为e，质量为m，运动速率为v，轨道半径为r.由玻尔轨道量子化条件，有

在库仑力作用下电子做圆周运动满足的方程为

取无穷远处电势为零，He+具有的电势能

评述He+离子中原子核带两个单位的正电荷，核外一个电子，与氢原子结构相仿，称为类氢离子，玻尔理论仍然成立.导出过程中所用的思维方法完全相同.

2.4 类氢原子模型

例4(清华大学2020年强基计划测试题)氢原子核外电荷若被粒子μ-取代，已知它的质量是电子的207倍，电荷与电子相同，则与电子相比，其基态的能量、角动量、轨道半径分别为原先的多少倍( ).

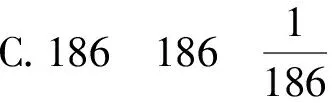
解析由例1知，处于基态的氢原子，其轨道半径及能级分别为

取氢原子核质量为电子质量m的1836倍；氢原子核外电荷若被粒子μ-取代，则系统的约化质量μ为

设氢原子基态能量为EH.若氢原子核外电荷被粒子μ-取代，基态能量记为Eμ，有

由玻尔轨道量子化条件，有

当n=1时，基态角动量相等.

设氢原子基态轨道半径为rH.若氢原子核外电荷被粒子μ-取代，基态轨道半径记为rμ，得

综上，正确选项是D.

点评分析μ-绕原子核的运动如同电子绕原子核的运动，分析中所使用的物理方法相同.基于玻尔氢原子模型的分析，氢原子核外电荷若被粒子μ-取代，则需要将电子的质量改为系统的约化质量.

2.5 奇特原子模型

例5 (2012清华保送生测试)物理学家在微观领域发现了“电子偶素”这一现象.所谓“电子偶素”就是由一个负电子和一个正电子绕它们的质量中心旋转形成的相对稳定的系统.已知正、负电子的质量均为m，电荷量大小均为e，普朗克常数h，静电力恒量k.

(1)用玻尔模型推算“电子偶素”的基态半径；

(2)求赖曼线产生光子的最高频率.

解析(1)由牛顿运动定律，有

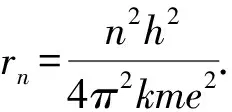
“电子偶素”系统具有的能量

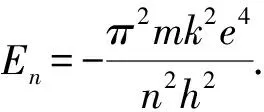
评述奇特原子类似氢原子体系，通常由μ±子、τ±子、π±介子、D±介子、正电子、反质子、Σ±超子和Ω-超子等粒子组成，它们分别取代普通原子中的电子、原子核或取代两者通过电磁作用形成的原子.其中原子核被取代的粒子称为粒子素.不难发现，例4中的μ-子替换电子后，氢原子成为奇特原子.本例中的“电子偶素”即由正电子取代原子核而成，“电子偶素”可视为类氢原子，显然玻尔理论仍适用.