基于超压和冲量的爆炸冲击波杀伤概率计算模型

张 毅,李志斌

(国防科技大学文理学院,湖南 长沙 410005)

随着时代的发展和科技的进步,各类化学材料越来越多地应用于人们的生产生活中,在产品生产和原料、废料的储存、运输等环节可能出现一系列的安全风险问题,国内外曾发生多起爆炸事故。2004年,罗马尼亚某村庄附近硝酸铵运输车发生爆炸,造成20人死亡,13人受伤。2013年,美国德克萨斯州一家化肥厂发生爆炸,造成35人死亡,260人受伤,多所房屋建筑受损。2015年,位于天津市滨海新区天津港的瑞海国际物流有限公司危险品仓库发生特别重大火灾爆炸,造成165人遇难,798人受伤,财产损失严重。2020年,黎巴嫩贝鲁特港口一个储存硝酸铵的仓库发生爆炸,造成至少190人死亡,6 500多人受伤。另外,在战场和各类军事行动中,爆炸同样是人员、建筑设施及武器装备的重要威胁之一。娄文韬等[1]研究了一种应用于城市反恐作战中爆炸杀伤率的评估模型,针对反恐怖行动中平民及恐怖分子两类目标的杀伤率进行分析;张舵等[2]从爆炸冲击的角度对飞机库目标毁伤特性进行数值模拟分析。本文从冲击波致伤的角度出发,提出了一种用于快速计算爆炸时超压和冲量变化致伤人体的人员伤亡概率计算模型,该模型能够预测和评估爆炸发生时的人员伤亡概率,为危险品的储存、运输以及爆炸事故的应急救援提供参考,同时可以应用于多种军事行动中,预测和评估因爆炸导致的人员损伤情况。

1 人员伤亡概率计算模型建立

1.1 爆炸致伤机制

根据致伤机制,爆炸伤一般分为四类[3-5]:一类损伤是指爆炸冲击波造成的伤害,冲击波直接作用于人体,导致人体组织或器官发生生理上或结构上的改变,与冲击波的超压和冲量密切相关,典型的冲击伤包括鼓膜破裂、肺损伤等;二类损伤是指爆炸时产生的破片对人体造成的伤害,损伤严重程度与破片命中位置和质量速度相关;三类损伤是指爆炸导致的人体位移出现的损伤,爆炸过程中的冲击波动压作用于人体可导致人员发生位移,进而引起抛投伤和碰撞伤;四类损伤是指爆炸时产生的高热、粉尘或有毒气体对人体造成的损伤。这四类损伤中,冲击伤和抛投伤与超压和冲量变化密切相关。

1.2 爆炸当量计算

常用的TNT当量计算方法有TNT当量法[6]、TNO多能模型、Baker-Strehlow模型等[7]。TNO多能模型和Baker-Strehlow模型更倾向于爆炸后果的预测,给出了无量纲峰值超压和无量纲距离的关系。相比而言,TNT当量法能够更加直观地给出TNT当量计算结果。TNT当量法的核心思想是根据能量相似原理,通过爆热计算爆炸物的TNT当量比:

(1)

式中,Eq为当量比,QTNT为TNT的爆热(kJ/kg),Q为某种炸药的爆热(kJ/kg)。

各类爆炸事故中,TNT当量的计算通常有三种方法:一是根据爆坑尺寸估计爆炸当量[8];二是根据爆炸时引起的地震波数据估算爆炸能量;三是根据爆炸发生时的火球大小及扩展速度估算爆炸能量[9]。Ambrosini等[8]通过实验的方法给出了适用于干燥黏土地面的爆坑尺寸经验公式:

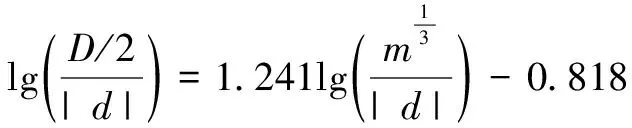
(2)

式中,D为爆坑直径(m),d为炸药设置高度(m),m为TNT当量(kg)。

1.3 爆炸威力场计算

爆炸是一个短时间内能量急剧释放的过程,剧烈变化的超压和冲量作用于人体可造成严重损伤。爆炸超压和冲量的计算方法有多种,针对球形TNT装药在空气中的爆炸,M.A.Sadovski等[10]根据大量实验结果,提出了如下超压和冲量关于TNT装药质量和距离的经验公式:

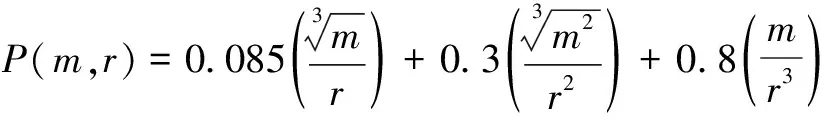
(3)

(4)

式中,P为爆炸超压(MPa),I为爆炸时的总冲量(Pa·s),m为TNT质量(kg),r为距爆炸中心的距离(m)。

Ps=P0·P′

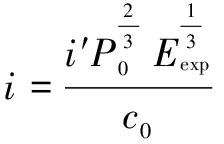
(5)

其中,P0为环境压强(Pa),P′和i′分别由式(6)和式(7)计算得到,Ps和i为最终计算的爆炸产生的峰值超压(Pa)和总冲量(Pa·s)。

(6)

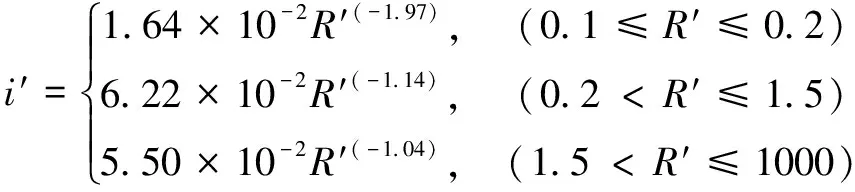
(7)

其中,R′为比例距离,计算公式如下:

(8)

式中,z表示距爆炸中心的距离(m),Eexp为爆炸能量(J)。

1.4 PROBIT概率计算方法

1.4.1 PROBIT模型描述

PROBIT模型是一种服从正态分布的线性模型,其最初的发展是为了分析、解决二值问题[12]。PROBIT模型应用于人员伤亡概率计算时,考虑了单个典型个体或类似群体在面对不同杀伤条件时的损伤耐受程度,将致伤因素和具体的伤亡情况通过概率联系起来。典型的PROBIT函数可以表示为

Y=Y(S)=k1+k2ln(S)

(9)

其中,Y表示PROBIT变量,S为“成因因子”,与考虑人员伤亡情况涉及的物理量相关联,本文的“成因因子”主要是爆炸引起的超压和冲量变化。k1和k2为拟合常数,由相关的实验数据确定,且需满足Y=5时对应的伤亡概率为50%。在此条件下,使用的正态函数的均值为μ=5,标准差σ=1,人员伤亡概率Pr(Y)为

(10)

1.4.2 PROBIT方程选择

爆炸时超压和冲量变化对人员的损伤主要包括冲击伤和抛投伤。人体内以肺为代表的含气组织和器官对于冲击波有非常敏感的响应,因此,肺损伤属于具有代表性的一种冲击伤;人耳鼓膜的破裂与爆炸的峰值超压密切相关,鼓膜破裂是另一个分析重点的冲击伤。抛投伤是冲击波效应使人员目标发生宏观位移时出现的损伤,常发生在人体位移后的减速撞击过程,主要包括:1)头部撞击损伤,碰撞发生时，头部属于较为易损的部位;2)全身撞击伤,这是由于撞击伤发生的部位不确定导致的。四种典型伤情的PROBIT方程如下所示[13-14]。

鼓膜破裂

Y1=-12.6+1.524lnPs

(11)

头部撞击损伤

(12)

全身撞击损伤

(13)

(14)

肺冲击伤

(15)

(16)

结合Lees等人[15]引用的真实爆炸数据,式(11)的鼓膜破裂预测值与实际情况基本一致;影响头部撞击损伤严重程度的关键在于人体发生位移时的速度,结合空气动力学相关知识[16],并充分考虑爆炸超压和冲量的影响,推导得到式(12)。因此，在分析这两种伤情时，可分别使用式(11)和式(12)。对于全身撞击损伤的PROBIT方程,式(14)仅考虑了冲量对于人员伤情的影响,而式(13)同时考虑了爆炸时的超压和冲量,更加符合爆炸现场的实际情况,因此，在计算时选用式(13)。肺冲击伤的PROBIT方程包括式(15)和式(16),式(15)在计算时考虑了有效压力Peff,式(16)直接使用了峰值超压进行计算。Baker等人[16]研究发现,当冲击波作用于人体时,有效压力与人体位置相对于冲击波传播方向有一定关系,这种相对位置关系分为三种:

1)人位于自由场且身体长轴垂直于冲击波传播方向,此时，有效压力为

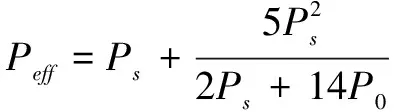
(17)

2)人位于自由场且身体长轴平行于冲击波传播方向,此时有效压力为

Peff=Ps

(18)

3)人位于冲击波的反射面附近,此时有效压力为

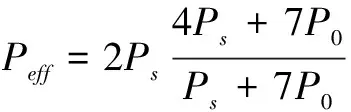
(19)

考虑人体相对于冲击波传播方向的位置关系,肺冲击伤的PROBIT方程选用式(15)。

1.4.3 爆炸超压和冲量与人员伤亡概率

通过1.1节对爆炸伤的分析,与爆炸超压和冲量相关的人员损伤主要包括冲击伤和抛投伤,针对这两类损伤,1.4.2节选取了四种具有代表性的伤情，并给出了对应的PROBIT方程。本小节中,利用Matlab软件进行计算,得到了爆炸超压和冲量变化与人员伤亡概率的关系,结果如图1所示。

图1 人员伤亡的P-I曲线

在鼓膜破裂的PROBIT公式(11)中,其“成因因子”仅与超压相关,因此，绘制的超压—冲量曲线为水平直线,当超压增大时,鼓膜破裂的百分比上升,如图1所示。图1中，实线和点线分别表示全身撞击损伤和头部撞击损伤在不同概率时的超压—冲量曲线,对比分析可知，头部撞击损伤对于超压和冲量的变化更为敏感。图1中，虚线表示自由场中人体长轴垂直于冲击波传播方向的肺冲击伤受超压和冲量变化的影响。

1.5 人员伤亡概率评估模型

爆炸超压和冲量杀伤人员的伤亡概率评估主要包含以下几个步骤。

1)根据爆炸物特点,选用合适的经验公式计算TNT当量;

2)根据得到的TNT当量计算爆炸杀伤威力场,分析威力场中超压和冲量的变化情况;

3)对于不同的损伤类型和伤情种类,选取合适的PROBIT公式计算对应的PROBIT变量值Y,最终得到在爆炸威力场中不同位置处的人员伤亡概率Pr(Y)。

2 案例分析

2.1 爆炸安全事故伤亡评估

本文基于以上人员伤亡概率评估模型,对江苏响水“3·21”爆炸事故人员伤亡情况进行分析。

2.1.1 事故描述

江苏响水天嘉宜化工有限公司位于江苏响水生态化工园区内,2019年3月21日14时45分,公司内部储存硝化废料的旧仓库冒出白烟,随即出现明火并迅速蔓延,至14时48分发生爆炸。该起爆炸事故造成78人死亡，76人重伤,640人住院治疗,直接经济损失高达19.8亿元[17]。图2是爆炸发生前后天嘉宜公司及其周边企业的情况。

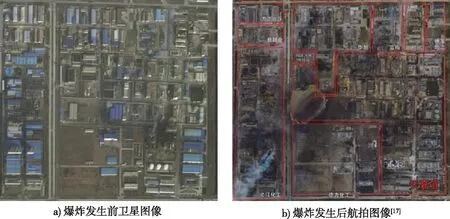
a)Satellite images before explosion b)Aerial image after explosion

2.1.2 TNT当量估计

调查显示,此次爆炸的爆炸物为该企业精制混二硝基苯过程中产生的硝化废料。该废料成分较为复杂,选用式(2)，根据爆炸形成的爆坑计算TNT当量。爆炸发生后,在爆炸中心产生了直径120 m的积水坑,如图3a)所示。经过排水后的测量,积水坑内存在一个此次爆炸形成的直径75 m、深1.7 m的爆坑,如图3b)所示。此次爆炸事故中起火爆炸的硝化废料总量大概在600 t左右,堆放在企业内的一个旧仓库内,爆炸物的质心高度约为0.5 m,根据式(2)计算得到TNT当量约为400 t。

a)Image of puddle formed after explosion b)Pit image after drainage

2.1.3 爆炸威力场计算

根据2.1.2节爆炸当量的计算结果,选用式(3)和式(4)计算爆炸时的超压和冲量变化,得到了超压和冲量与距爆炸中心距离的关系,如图4所示。由图可知,超压在空气中衰减的速度比冲量下降趋势更快,在距离为200 m时,超压衰减至0.11 MPa,基本接近一个标准大气压。

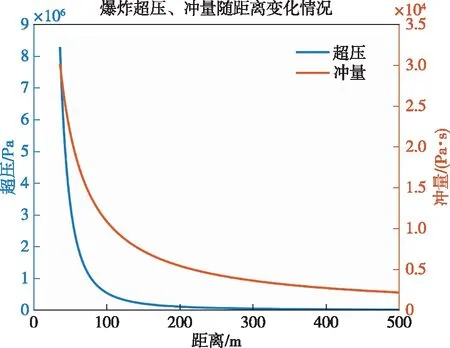
图4 爆炸超压和冲量随距离变化情况

2.1.4 人员伤亡概率计算

基于Matlab软件,在得到爆炸杀伤威力场的基础上,结合1.4节提出的PROBIT概率计算方法,先根据伤情类型选取对应的PROBIT方程计算概率变量Y,再利用式(10)得到人员的伤亡概率Pr(Y)。概率变量Y的“成因因子”为爆炸威力场中的超压和冲量,而超压和冲量这两个物理量与距爆炸中心的距离和爆炸当量相关。当爆炸的当量一定时,概率变量Y可以视为距离的函数,因此，最终得到的人员伤亡概率为距爆炸中心距离的函数。图5为计算得到的四种伤情的损伤概率随距离变化关系图。由图可知,在爆炸中心100 m范围内,鼓膜破裂的概率高于99%,随着距离的增加,损伤概率逐渐降低。肺冲击伤、头部撞击损伤和全身撞击损伤均属于较为严重的致死类伤,其中,在肺冲击伤计算中,人员与冲击波的相对位置关系为人员位于自由场且身体长轴垂直于冲击波传播方向。对比分析图5中的三条损伤曲线可知,这三种伤情中，对人体损伤最大的是头部撞击损伤,这与1.4.3节中得到的三类损伤的超压—冲量曲线一致。

图5 人员损伤概率随距离变化情况

2.1.5 结果分析

根据本文提出的人员伤亡概率计算模型,对江苏响水天嘉宜化工有限公司爆炸事故相关结果分析如下。

1)TNT当量结果分析

采用Ambrosini等人提出的经验公式,根据爆炸现场的爆坑大小估算得到爆炸的TNT当量约为400 t,与此次爆炸事故的调查报告显示的260 t有差距。其原因主要有以下两个方面:1)经验公式是基于实验结果总结的,实验环境的土地条件和此次爆炸事故的土地条件存在差别,导致使用公式计算的当量是一个存在误差的估计值而非精确值;2)此次爆炸物为该企业存放的硝化废料,堆放的特点是占地面积大而总体的高度较低,这导致在发生爆炸时爆坑的直径偏大而深度偏小。Ambrosini等人在实验中使用的是球形炸药,实验中爆坑直径和深度的比值更小。基于这两方面原因,本文计算的TNT当量相对事故调查报告中给出的当量偏大。

2)人员伤亡结果分析

由2.4节的计算结果可知,在三类致命损伤中,头部撞击损伤带来的威胁更大,在距爆炸中心200 m处,人员由于头部撞击损伤的伤亡概率高达99%,随着距离增加伤亡概率迅速降低,在距爆炸中心250 m处，概率降至1%,由此可得，此次爆炸事故中人员损伤的安全距离为250 m。图6为公布的78位遇难者身份及位置分布,80%的遇难者在距爆炸中心300 m范围内,60%的遇难者在距爆炸中心250 m范围内。所有遇难者死亡的地点可以分为三类:第一类是位于自由场中,且直面爆炸中心而没有任何建筑的遮挡;第二类是位于建筑物内部;第三类是位于建筑背向爆炸中心的一侧。与第一类不同,第二类和第三类死亡地点出现的人员伤亡更多是因为建筑本身受损而造成的，而本文计算的伤亡概率是基于自由场中的爆炸超压和冲量变化,与第一类遇难地点相对应。将计算得到的250 m安全距离与遇难者位置分布图对比,发现事故中的第一类遇难地点均位于距爆炸中心250 m范围内,这与计算结果相符合。

图6 响水爆炸事故遇难者分布位置[17]

2.2 战场爆炸伤亡评估

结合第一节建立的人员伤亡概率评估模型,对俄乌冲突中某典型弹药的冲击波杀伤概率进行分析。

2.2.1 弹药概述

2022年6月初,俄罗斯向乌克兰某外国雇佣兵训练基地发射两枚空基高超声速导弹,致使该基地中超过70%的人员死亡。“匕首”导弹是俄罗斯在“伊斯坎德尔-M”导弹基础上研制的空基高超声速导弹,与俄9M723型导弹相似,该导弹总质量3.8 t,弹头大约重500 kg,最大飞行速度可达10Ma[18]。

2.2.2 TNT当量估算

目前,世界各国普遍使用的高能炸药是奥克托今(HMX)和黑索金(RDX),两种炸药的爆热分别是5 673 kJ/kg和6 025 kJ/kg。“匕首”导弹的战斗部重500 kg,参考一般高爆弹头中炸药质量占比,利用式(1)计算得到导弹爆炸当量约为500～530 kg。

2.2.3 爆炸威力场与杀伤概率计算

根据2.2.2节爆炸当量的计算结果,用式(3)和式(4)计算在该爆炸当量下超压和冲量随距离的变化情况。根据1.4节中的PROBIT概率计算方法,选用表1中的式(11)、(12)、(13)和(15)分别计算鼓膜破裂损伤、头部撞击损伤、全身撞击损伤和肺冲击伤对应的PROBIT变量Y,并利用式(10)得到四种典型伤情的损伤概率Pr(Y)。其中,肺冲击伤、全身撞击损伤和头部撞击损伤的安全距离如图7a)所示。鼓膜破裂损伤与距离的关系如图7b)所示。

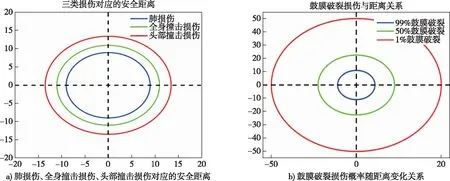
a)Safety distance corresponding to lung injury, whole body impact injury and head impact injury b)Relationship between damage probability of tympanic membrane rupture and distance

2.2.4 结果分析

计算结果表明,四类损伤中鼓膜破裂伤对于冲击波作用最为敏感,在距爆炸中心50 m处,鼓膜破裂概率下降为1%,此时，超压约为24 kPa,与Hirsch等人[16]得到的人耳鼓膜破裂阈值34.5 kPa(5psi)十分接近。对比肺冲击伤、头部撞击损伤和全身撞击损伤三种伤情的安全距离可知,在同一爆炸冲击波威力场内,若人员未携带防护装具,对人员威胁最大的是头部撞击损伤,肺冲击伤威胁最小。但如果人员带有防护装备,头部撞击损伤和全身撞击损伤的伤亡风险概率会降低,且肺冲击伤受到的影响较小。

3 结束语

本文建立了一种用于评估人员在爆炸威力场中的伤亡概率的计算模型,能够从超压和冲量变化的角度对爆炸造成的人员伤亡概率进行计算。以江苏响水天嘉宜化工有限公司的爆炸事故为例,基于Matlab软件计算了事故的爆炸当量及爆炸范围内的超压和冲量变化,使用PROBIT方法得到了鼓膜破裂、肺冲击伤、全身撞击损伤和头部撞击损伤四类典型伤情损伤概率与距爆炸中心距离的关系,并对事故相关结果进行分析,得到了此次爆炸事故存在的安全距离，并且评估了某弹药的冲击波杀伤概率,结合四种伤情相对应的安全距离，简要分析了不同伤情在不同条件下对人员的影响程度。本文所提出的模型可用于爆炸事故或战场爆炸情况中人员伤亡概率的评估,对评估部分武器弹药的毁伤范围也有一定参考意义。

本文建立的人员伤亡概率计算模型仅考虑了自由场的超压和冲量变化,在实际的爆炸事故中,还存在建筑物倒塌、建筑物碎片造成的人员损伤，战场中各类弹药发生的爆炸也需要考虑破片的威胁性。下一步将从这几方面进一步完善计算模型。