基于多尺度分割方法的斜坡单元划分及滑坡易发性预测

常志璐，黄发明，蒋水华，张崟琅，周创兵，黄劲松,3

(1.南昌大学 工程建设学院，江西 南昌 330031；2.帕多瓦大学 地质科学院，意大利 帕多瓦 35131；3.纽卡斯尔大学 岩土科学与工程卓越研究中心，澳大利亚 纽卡斯尔 2287)

滑坡是中国发生最频繁、危害最大的地质灾害类型之一，给当地居民的人身和财产安全造成巨大损失[1–2]。区域滑坡易发性预测是一种预测潜在滑坡空间位置的有效途径，可以准确地预测“潜在滑坡”发育的空间概率[3–4]。其评价过程主要包括：构建历史滑坡数据库、划分制图单元、提取研究区域的环境因子、构建易发性预测模型、模型的精度评价和绘制区域滑坡易发性图[5–8]。其中，历史滑坡数据主要通过历史影像识别和野外实地调查获得[9]，易发性模型的预测精度主要通过ROC曲线和频率比精度两种方法评价，滑坡易发性图主要分为极高、高、中等、低和极低5个等级[10]。

当前的滑坡易发性制图单元主要有栅格单元、地域单元、均一条件单元、斜坡单元和地貌单元[6,11]。其中，栅格单元和斜坡单元应用最广泛。栅格单元具有形状规则、便于快速剖分、模型计算效率高等优点，但难以表达真实地形地貌且与基础环境因子联系不够紧密，导致预测结果缺乏明确的物理意义。另外，栅格单元的预测结果难以准确定位具体滑坡位置和范围。与栅格单元相比，斜坡单元依据真实地形地貌进行划分，具有较明确的地质特征意义，能够相对准确地反映滑坡区域的不同地形特征。因此，越来越多的学者尝试利用斜坡单元进行区域滑坡易发性预测。但是，如何快速准确地自动划分斜坡单元仍是目前阻碍斜坡单元应用的主要因素。

目前，应用最广泛的斜坡单元划分方法是水文分析法[12–13]。该方法将斜坡单元定义为分水线和汇水线围成的一块区域，借助ArcGIS软件和通过正反向DEM水文过程分析划分斜坡单元。但是，该方法获得的斜坡单元过于零散、数量众多且难以调控，可操作性和自动化程度很低，需要大量的后期人工修正。另外，分水线和汇水线围成的一块区域可以是一个单坡或多个斜坡，甚至可以是一个小流域。在实际应用过程中，一些学者对水文分析法进行了修正。例如，张曦[14]和颜阁[15]等提出了曲率分水岭法，通过正反向曲率分别提取出凸型和凹型地貌元素，但是，这些方法本质仍然属于基于正反向曲率地表水文过程分析的范畴。近年来，研究者对斜坡单元进行了新的定义，例如：Jia等[16]认为斜坡单元需要确保内部最大均质性和不同单元之间的最大异质性；王凯等[11]基于滑坡稳定性力学分析的均一性基本假定，将斜坡单元定义为三维空间中的一个连续、均质且闭合的小区域。基于此，出现了一些新的斜坡单元划分方法。例如：Alvioli等[17]基于斜坡单元的最大均质化定义，提出一种新的斜坡单元提取方法r.slopeunits，该方法在斜坡单元提取结果的精细化和均质化程度上比传统方法有所进步；Wang等[18]建立一种新的斜坡单元提取方法MIA–HSU，利用形态影像学算法提取山脊、山谷形态骨架线。虽然当前斜坡单元提取方法取得了一些进展，但是，仍然存在不足之处，主要表现在：1）难以适用于缺乏高精度DEM的地区，2）难以快速准确地实现自动提取斜坡单元，3）提取结果受人为设定的阈值影响[11]。

选择合适的环境因子是区域滑坡易发性预测过程中的重要步骤，输入变量信息的质量直接决定着模型的优劣和易发性结果的准确性。在采用斜坡单元进行滑坡易发性建模时，需要提取每个斜坡单元内部的环境因子信息。目前，最常采用的方法是基于一定分辨率的环境因子栅格数据，通过ArcGIS 10.2软件“空间分析”工具中的区域分析功能，分别提取每个斜坡单元范围内环境因子栅格值的平均值（连续型数据）或众数值（离散型数据）作为这个斜坡单元的环境因子值[19]。但是，由于各个环境因子在空间上具有空间变异性，例如一些地形因子（如高程、坡度、剖面曲率等）在不同位置表现出较高的变异性，而岩性、坡向等环境因子在斜坡单元中变异性较小。并且，一个斜坡单元内可能包含几百个栅格数据，仅仅采用平均值无法准确反映斜坡单元内部的真实情况，造成数据信息的过度简化和缺失。因此，为了获得更加准确的滑坡易发性预测模型和结果，应该充分考虑和挖掘斜坡单元内部环境因子的空间非均质性。

常用的滑坡易发性预测模型主要分为：基于滑坡编录的概率分析模型、启发式模型、确定性模型、数学统计模型和人工智能模型[20]。其中，人工智能模型能有效解决统计模型预测区域滑坡易发性时存在的问题，并得到了广泛的应用，主要包括逻辑回归（logistic regression, LR）[21]、人工神经网络[22]、支持向量机（support vector machine, SVM）[23]、模糊逻辑[24]、决策树和随机森林[25]模型等，其中SVM和LR模型应用最多并且评价效果最好。

综上所述，本文以江西省崇义县为例，基于多尺度分割算法提出一种斜坡单元划分方法，充分考虑斜坡单元内部环境因子的空间变异性，选取均值、变化值和标准差3个变量表征斜坡单元内部环境因子的非均质性，并分别采用SVM和LR模型来预测并绘制研究区域滑坡易发性图。

1 方 法

1.1 滑坡易发性建模流程

本研究基于斜坡单元和斜坡单元内部环境因子的非均质性特征，采用机器学习模型构建了区域滑坡易发性的预测模型，具体建模步骤如下：

1）基础数据的收集。从国家地质调查局网站及91位图助手软件下载DEM影像图（分辨率为8.9 m）、Landsat TM8遥感影像1景（2013–07–03，轨道号119/041）、地层图（1∶25 000）、地表覆被、人类工程活动和历史滑坡数据库，并通过ArcGIS10.2软件进行管理。

2）斜坡单元的划分。从研究区域DEM图层中通过ArcGIS10.2分别提取坡向和地形阴影图，采用多尺度分割方法划分斜坡单元，分别对斜坡单元进行定性定量评价，并与传统的水文方法划分的斜坡单元进行对比分析。

3）环境因子的提取。基于斜坡单元，分别提取研究区域的地形地貌、地层、水文、地表覆被和人类工程活动因素，考虑斜坡单元内部环境因子的变异性，分别采用平均值、变化值和标准差3个变量表征每一个环境因子。随后对所有环境因子变量进行相关性分析。

4）样本数据集的构建。根据历史滑坡信息分别提取滑坡样本的环境因子信息，在非滑坡区域随机选取与滑坡样本相同数量的非滑坡样本并提取相应的环境因子信息，滑坡和非滑坡样本信息共同构成建模的基本数据集。

5）易发性预测模型构建。选择机器学习模型（SVM和LR模型）分别构建基于斜坡单元的易发性预测模型（Slope–SVM/LR模型）和考虑斜坡单元内部环境因子非均质性的易发性预测模型（Variant Slope–SVM/LR模型）。

6）模型精度评价。分别采用ROC曲线和频率比精度对比上述4个模型的预测精度。

7）绘制全区易发性图。将全区数据导入各个易发性预测模型以预测易发性指数，使用自然间断点法将其划分为极高、高、中、低和极低5个易发性等级，绘制滑坡易发性图。

1.2 斜坡单元的提取

1.2.1 基于多尺度分割算法的斜坡单元划分

多尺度分割（multi-scale segmentation method，MSS）的核心算法是基于异质性最小区域合并算法，使对象内部的异质性最小，对象之间的异质性最大[26]。MSS方法是一种采用自底向上的区域增长法，即基于像素层自底向上区域合并完成对象提取。基于MSS方法的基本原理，可以将斜坡单元定义为连续、均匀、封闭的对象，在特定的分割尺度阈值下，呈现出对象内部异质性最小和相邻对象之间异质性最大的特征。

MSS方法提取斜坡单元的流程示意图如图1所示。具体步骤为：

图1 MSS方法提取斜坡单元流程图Fig. 1 Flowchart for slope unit extraction by MSS method

1）收集研究区域的基础高程影像图和历史滑坡数据库。分别提取坡向和山体阴影图作为MSS方法的基本输入影像，另外，统计所有历史滑坡的形态和尺度特征。

2）参数的设置。MSS方法中需要设置的参数包括尺度、形状特征权重和紧致度权重参数，通过试错法并结合研究区域内历史滑坡的形态和尺度特征（修正试错法）来确定。

3）斜坡单元的划分。从像素层开始，先将相邻区域特征相似的像素聚合成小影像区域。然后将相似的小影像区域基于异质性最小原则合并成大的影像区域，每一次合并，都计算两区域合并后区域的异质性是否大于尺度阈值（scale）。若大于尺度阈值，则不对该两区域进行合并；若小于尺度阈值，则进行合并，生成新的更大的影像区域。直至合并后的区域的异质性都大于尺度阈值，或所有的区域都合并完毕，则停止合并[27]。

4）后处理优化过程。将步骤3）中的影像对象进行分割、合并和平滑等优化处理，消除局部“孤岛效应”的对象，最后获得研究区域内的斜坡单元。

1.2.2 输入影像和参数设置

在采用MSS方法划分斜坡单元时，选取坡向和山体阴影图作为基本的输入影像。其中，山体阴影是一种由光源和高程表面的坡度和坡向确定地形的技术，可以反映一定的地形信息，其影像灰度值介于0～255之间。坡向定义为坡面法线在水平面上投影的方向，可以用来识别地面上某个位置的最陡下降方向。因此，根据坡向和地形阴影的特征，MSS方法可以最大限度地提高坡单元内部的均匀性，最大限度地提高斜坡单元之间的非均匀性。

MSS方法中需要设置的参数主要包括尺度、形状特征权重和紧致度权重。若尺度参数取值太大，则会出现分割不完全的现象；反之，则会出现分割破碎的现象。最优尺度应该表现为：对象大小与地物目标轮廓相当，大小接近；对象多边形既不能太破碎，也不能边界模糊，且光谱变异情况较小。紧致度参数是用来描述对象单元的饱满程度，即接近正方形和接近圆形的程度。紧致度权重越高，图像对象越紧凑，对象单元的形状越规则。因为影像数据中最重要的信息是光谱信息，形状特征的权重太高会降低分割结果的质量。

1.2.3 最优参数组合的确定

参数组合的选择直接决定着斜坡单元的划分结果，本研究通过修正试错法来选择最佳的参数组合。具体步骤如下：

1）根据历史滑坡数据库，计算研究区域内滑坡的面积和形状特征。形状特征通过形状指数（R值）来表示，R值可以通过式（1）计算获得：

式中，L、S分别为滑坡面的周长和面积。

2）根据传统的试错法确定几组参数值，分别采用每一个参数组合来划分斜坡单元。

3）分别计算每组参数组合条件下斜坡单元面积和形状指数的平均值和标准差，并与滑坡面积和形状指数的平均值和标准差做比较。当划分的斜坡单元面积和形状指数的平均值和标准差是滑坡相应数据的1～2倍，并且R值介于16.00～20.78之间时，认为划分的斜坡单元是合理的，其对应的参数组合是最优组合。

1.3 机器学习模型

1.3.1 支持向量机模型

1.3.2 逻辑回归模型

LR模型是一种能有效处理二元分类问题的非线性回归模型，其基本思想是寻找最佳拟合函数来表示目标变量与因子变量之间的相关关系[30–31]。假设变量因子为xi(i=1,2,···,l)，目标变量为y=0和1。LR模型计算公式如式（3）和（4）所示：

式（3）～（4）中：z为变量叠加后的线性权重值之和；a为LR模型常数；bl为LR模型的系数；p为事件发生的概率，其值域为[0,1]。

2 案例研究

2.1 崇义县概况

崇义县位于江西省西南部，介于113°55′E ～ 114°38′E，25°24′N ～ 25°55′N之间，总面积约2 206.3 km2。崇义县属于赣南丘陵区，海拔在140～2 019 m之间。地形主要为中、低山（≥500 m）、丘陵（300～500 m）和河谷阶地（≤300 m），分别占总面积的47.67%、45.06%和7.27%。县域地质单元十分复杂，包括寒武纪至泥盆纪期间的变质岩（变质细砂岩和板岩）、碳酸盐岩（石灰岩）、火成岩（花岗岩）及碎屑岩等。该地区属亚热带季风气候，雨量充沛，湿度较高。年平均降雨量达1 615.2 mm，平均气温约为17.8℃。土地覆盖类型主要包括森林、农田、草地和水体。

2.2 滑坡编录信息

野外滑坡编录主要包括滑坡的位置、发生时间、基本环境因子信息、运动模式、规模大小及诱发因素等信息。根据崇义县自然资源局的数据和野外调查可知：县域内自1970年至今共发生滑坡254次，其分布如图2所示。滑坡主要为覆盖层滑坡，具有规模小、群发性的特点。滑坡体主要为第四系残坡积层，由粉质黏土夹层和碎块石组成。滑坡面积介于在4.2×103～3.2×104m2之间，平均面积约为7.6×103m2。滑坡厚度在2.8～8.0 m之间。研究区域内的滑坡分布不均匀，北部滑坡较多，东部滑坡较少。

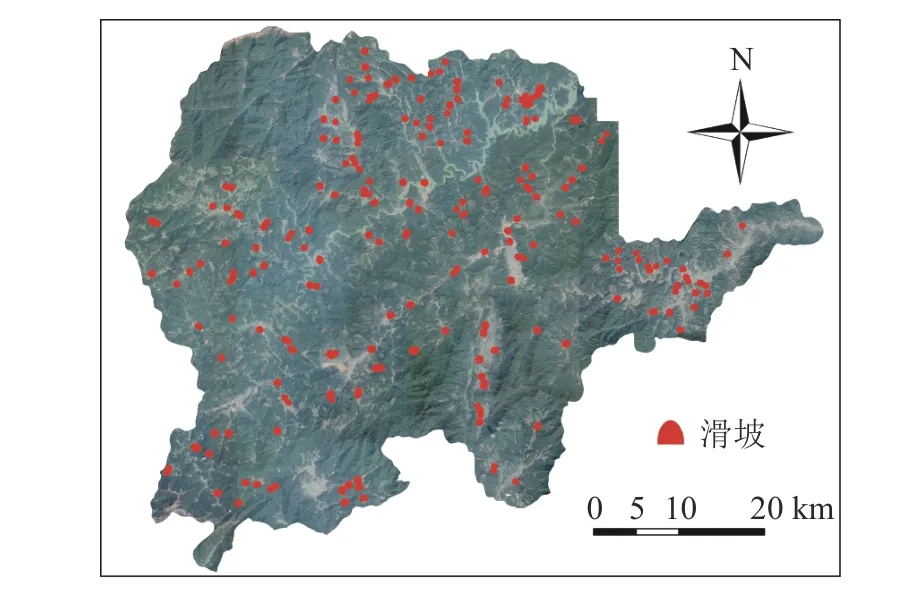
图2 崇义县滑坡分布Fig. 2 Distribution of landslides in Chongyi County

2.3 采用MSS方法划分斜坡单元

基于分辨率为8.9 m的DEM数据，通过ArcGIS软件分别提取坡向和山体阴影图作为MSS方法的输入图像，研究区域的山体阴影和坡向图如图3所示。在尺度、形状特征权重和紧致度权重参数组合中，尺度参数分别取10、20、30、40和50，形状特征权重参数分别取0.5、0.6、0.7、0.8 和0.9，紧致度权重参数也分别取0.5、0.6、0.7、0.8和0.9，在每一组参数组合下，分别采用MSS方法划分斜坡单元。根据研究区域的地形特征，分别在丘陵区和中低山区各选取一个区域（图3），对比分析斜坡单元的划分效果。

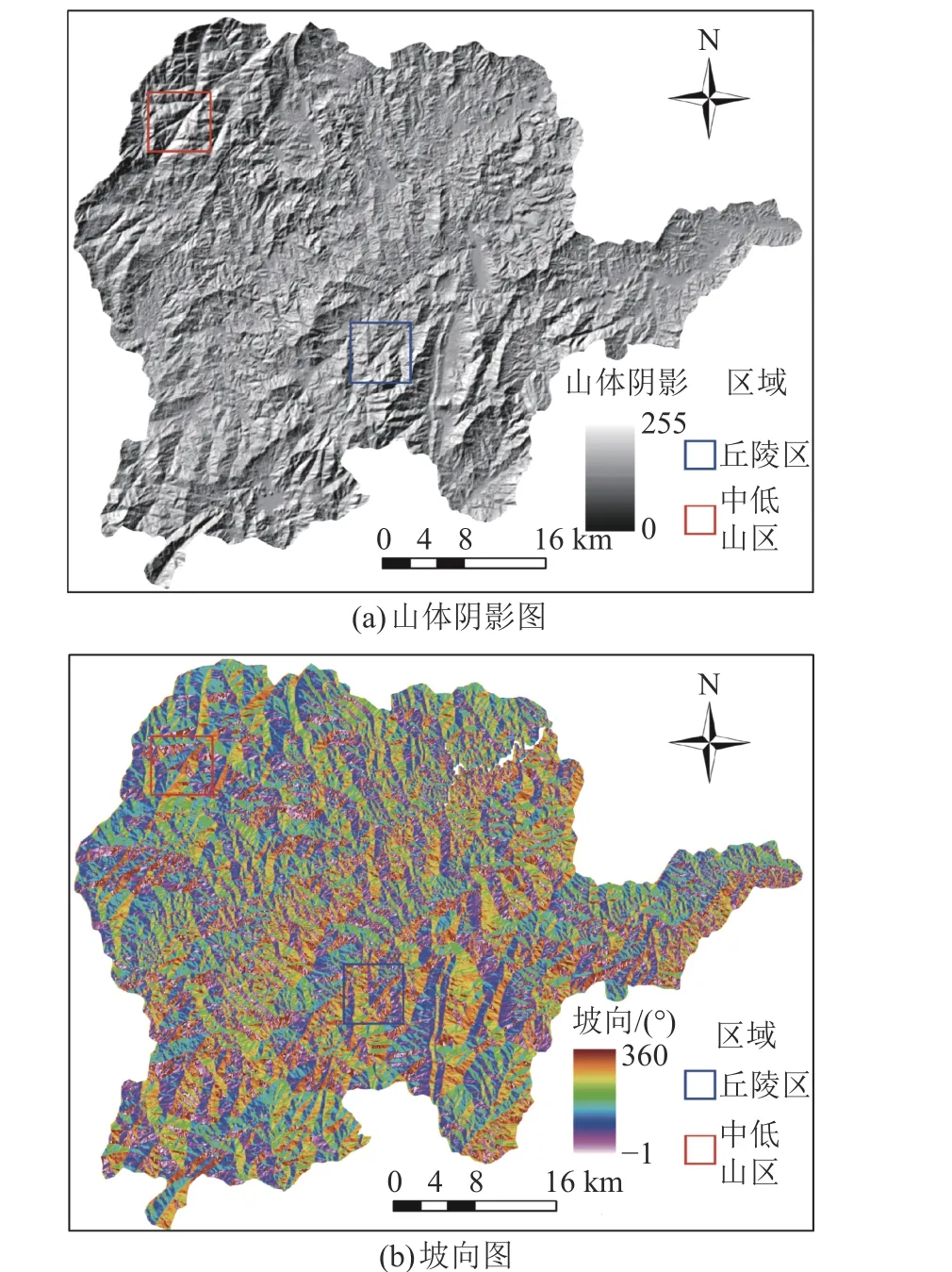
图3 山体阴影和坡向图Fig. 3 Shaded relief and aspect images

2.4 基于斜坡单元的环境因子的提取

通过崇义县滑坡发育特征和自然地理分析并参考相关文献[20–21]，最后选择高程、坡度、坡向、平面曲率、剖面曲率、地形起伏度、岩土类型、地形湿度指数（topographic wetness index，TWI）、归一化植被指数（normalized difference vegetation index, NDVI）、归一化建筑指数（normalized difference building index,NDBI）和斜坡单元形态等15个环境因子。考虑斜坡单元内部环境因子的非均质性时，每一个环境因子可以采用平均值、变化值和标准差3个变量表征。其中，需要说明的是离散型变量（岩性、坡向）采用众数来表示，无法获得类似的3个变量。因此，考虑斜坡单元内部连续型环境因子的非均质性时，可将15个环境因子扩展为38个环境因子。其中，斜坡单元形态特征主要通过斜坡单元的形状指数和紧致度来表征。

为了降低环境因子之间的多重共线性对模型构建的影响，需要对38个环境因子进行相关性分析。38个环境因子时间的相关系数可以通过SPSS 22软件计算获得，当两个变量相关系数的绝对值小于0.3时，认为两个变量之间无相关性。根据该规则，本研究共有22个环境因子的相关系数小于0.3，主要包括：高程、高程变化值、坡度、坡度变化值、坡度标准差、剖面曲率、平面曲率、平面曲率变化值、平面曲率标准差、TWI、NDVI、NDBI、公路密度、公路密度变化值、河流密度、河流密度变化值、覆盖层厚度、形状指数、紧致度、坡向、岩土类型和距水系距离。其部分环境因子的空间分布如图4所示。

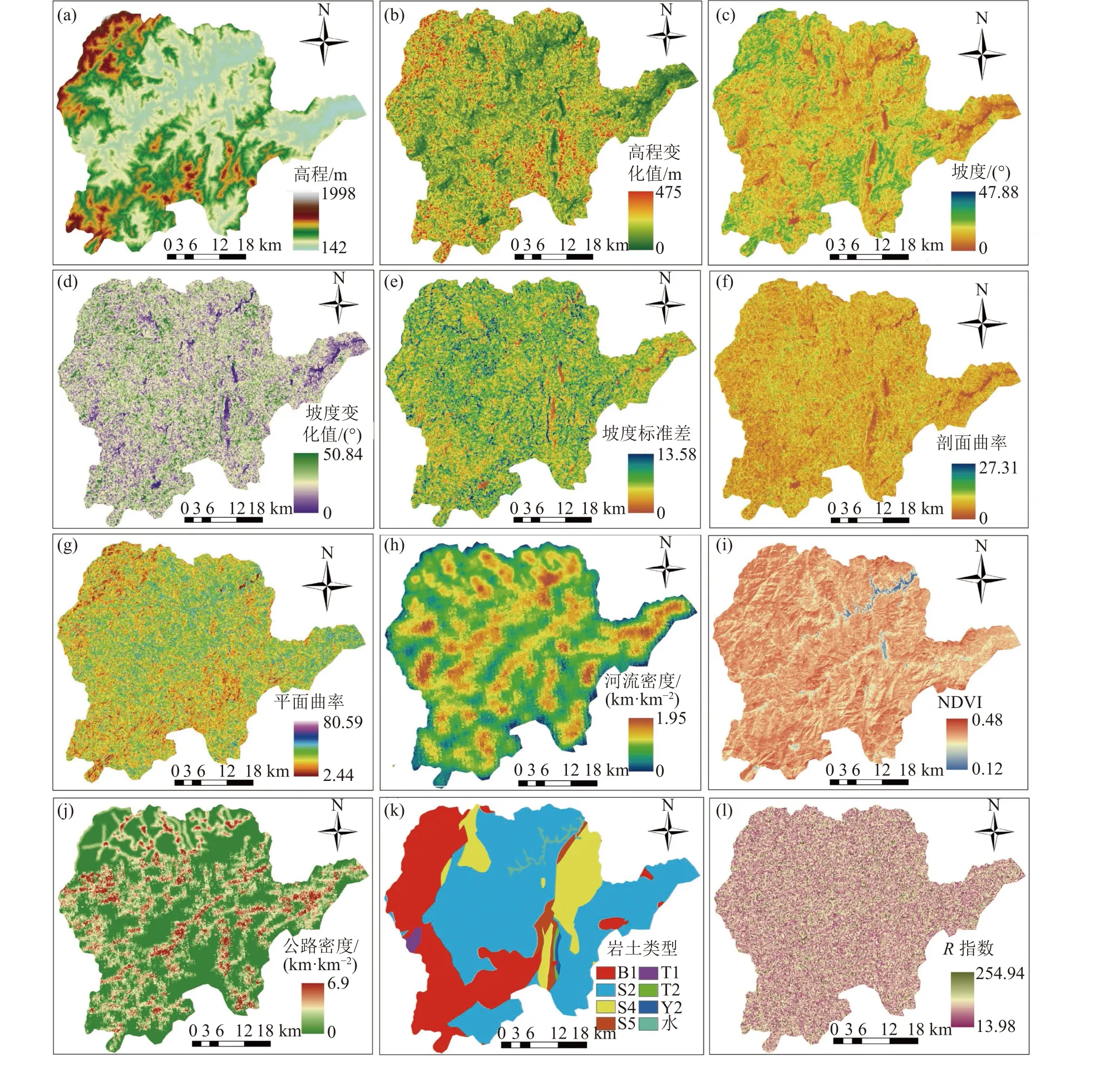
图4 研究区域环境因子空间分布Fig. 4 Conditioning factor maps in study area

2.5 基于斜坡单元的机器学习模型构建

将上述的22个环境因子的信息作为机器学习模型的输入变量，模型的输出变量为1（滑坡）和0（非滑坡）。其中，输入变量主要包括滑坡样本（标签值为1）和非滑坡样本（标签值为0），按一定比例划分为训练集和测试集，分别用于训练机器学习模型和测试机器学习模型。本研究中，滑坡样本是历史滑坡所在斜坡单元，非滑坡样本是从滑坡区之外的斜坡单元内随机选取与滑坡斜坡单元相同数量的斜坡单元。滑坡样本和非滑坡样本按7∶3的比例划分为训练集和测试集。

3 滑坡易发性预测结果分析

3.1 斜坡单元划分

根据MSS方法在不同参数组合条件下斜坡单元的划分结果，分别统计了不同参数组合条件下斜坡单元的面积和形状指数特征，如表1所示。从表1可以看出，当尺度、形状特征权重和紧致度权重分别为20、0.8和0.8时，划分的斜坡单元的面积和形状指数统计特征与研究区域历史滑坡的统计特征最相近，斜坡单元划分效果最好。因此，研究区域共被划分为53 05 5个斜坡单元。 区域内MSS方法和水文法分别在丘陵区和中低山区的斜坡单元划分结果如图5所示。从图5可以看出：MSS方法适用于不同地形地貌条件下的斜坡单元划分。与传统的水文法划分的斜坡单元结果相比， MSS方法划分的斜坡单元更均匀，更符合斜坡的实际地形地貌条件，避免出现斜坡单元面积过大和多个斜坡包含在同一个斜坡单元内的错误。另外，MSS方法划分的斜坡单元形状更规则，不存在狭长细条状的斜坡单元，不需要进行人工调整。

图5 典型区域MSS方法和水文法的斜坡单元划分结果Fig. 5 Slope units of typical cases divided by MSS and hydrological methods

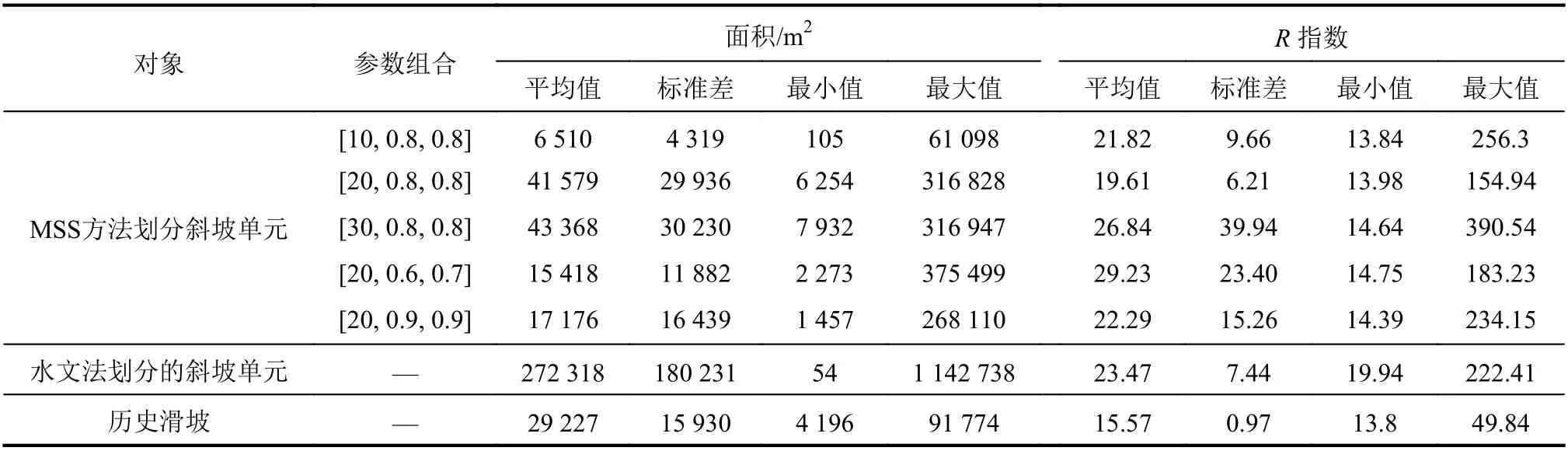
表1 斜坡单元面积和形状指数统计特征Tab. 1 Statistical characteristics of the area and shape index (R index) for slope units

3.2 斜坡单元的定性定量评价

3.2.1 斜坡单元的定性评价

通过对比滑坡及其所在的斜坡单元之间的空间位置关系可以定性地评价MSS方法划分斜坡单元的效果。如果滑坡的位置与其所在的斜坡单元存在一一对应的关系，则认为提取的斜坡单元是合理的。

基于MSS方法和水文法的斜坡单元划分结果，历史滑坡与其所在的斜坡单元之间的空间位置关系如图6所示。从图6（a）可以看出，MSS方法划分的斜坡单元内，大部分的滑坡与其所在的斜坡单元存在一一对应关系，局部出现少量滑坡跨越两个斜坡单元。对此，本文主要通过两种方式进行处理，一种是根据实际地形对斜坡单元进行验证和调整；另一种方法是计算滑坡在跨越斜坡单元中的面积分布，选择面积最大的斜坡单元作为滑坡所在斜坡单元。但是，在水文法划分的斜坡单元内，发现存在多个滑坡分布在同一个斜坡单元的情况，如图6（b）所示。图6的结果表明，相比于水文分析法，采用MSS方法划分的斜坡单元更合理。

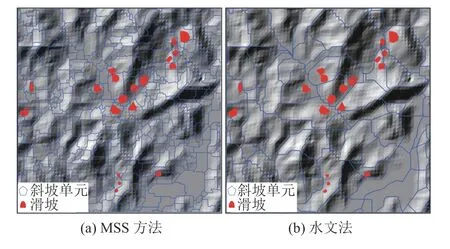
图6 历史滑坡与其所在的斜坡单元之间的空间位置关系Fig. 6 Position relationship between the recorded landslides and the responding slope units

3.2.2 斜坡单元的定量评价

斜坡单元的大小和形状特征可以用来定量评价MSS方法划分斜坡单元的效果。基于MSS方法划分斜坡单元的大小和形状参数分布特征如图7所示。其中，斜坡单元的大小用面积来表示。图7（a）显示了斜坡单元的面积值分布特征，74.92%的斜坡单元的面积介于10 000～60 000 m2。斜坡单元的平均值、标准差、最大值及最小值分别是41 579 m2、29 936 m2、6 254 m2和316 828 m2（见表1）。斜坡单元的形状特征可以采用R指数来表示。已知圆、正方形和三角形的R值分别是4π、16和20.78。斜坡单元的形态越接近于长条状，R值越大；并且，当R值大于28时，斜坡单元的长宽比约为5∶1。表1中显示斜坡单元的形状指数的平均值、标准差、最小值及最大值分别是19.61、6.21、13.98和154.94。从图7（b）中可以看出，68.82%的斜坡单元的R值介于18～26之间，表示斜坡单元的形状介于三角形和正方形之间，并且均匀性更强。

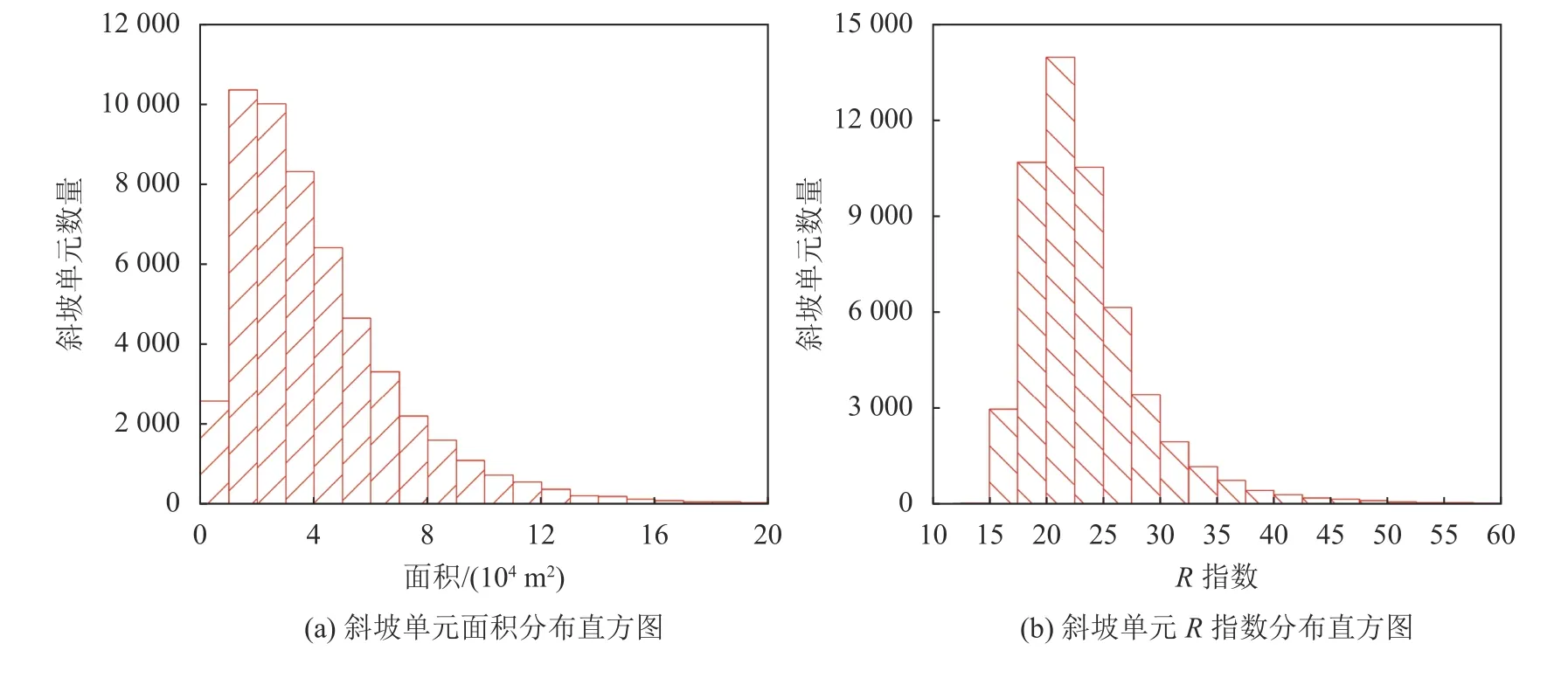
图7 MSS方法划分的斜坡单元的面积和形状参数分布特征Fig. 7 Distribution characteristics of the area and shape indexes of slope units by the MSS method

3.3 易发性制图

本研究分别使用Slope–SVM、Variant Slope–SVM、Slope–LR和Variant Slope–LR模型，计算整个区域的易发性指数。然后在ArcGIS10.2 软件中采用自然间断点法将易发性指数划分为极高、高、中等、低和极低5个等级，不同评价模型的易发性分布如图8所示。图8（a）显示出Slope–SVM模型中极低、低、中、高和极高易发性等级分别占比32.18%、20.46%、14.91%、13.62%和18.82%。图8（c）显示出Variant slope–SVM模型中极低、低、中、高和极高易发性等级分别占比41.85%、17.68%、12.75%、11.99%和15.73%。Slope–LR和Variant slope–LR模型的滑坡易发性分布如图8（b）、（d）所示。上述模型的易发性分布显示出研究区域的高易发性等级主要分布在区域的东部和中部，呈带状分布。相比于Slope–SVM/LR模型的预测结果，Variant Slope–SVM/LR模型中的极低和低易发性的比例增加，高和极高易发性比例降低。

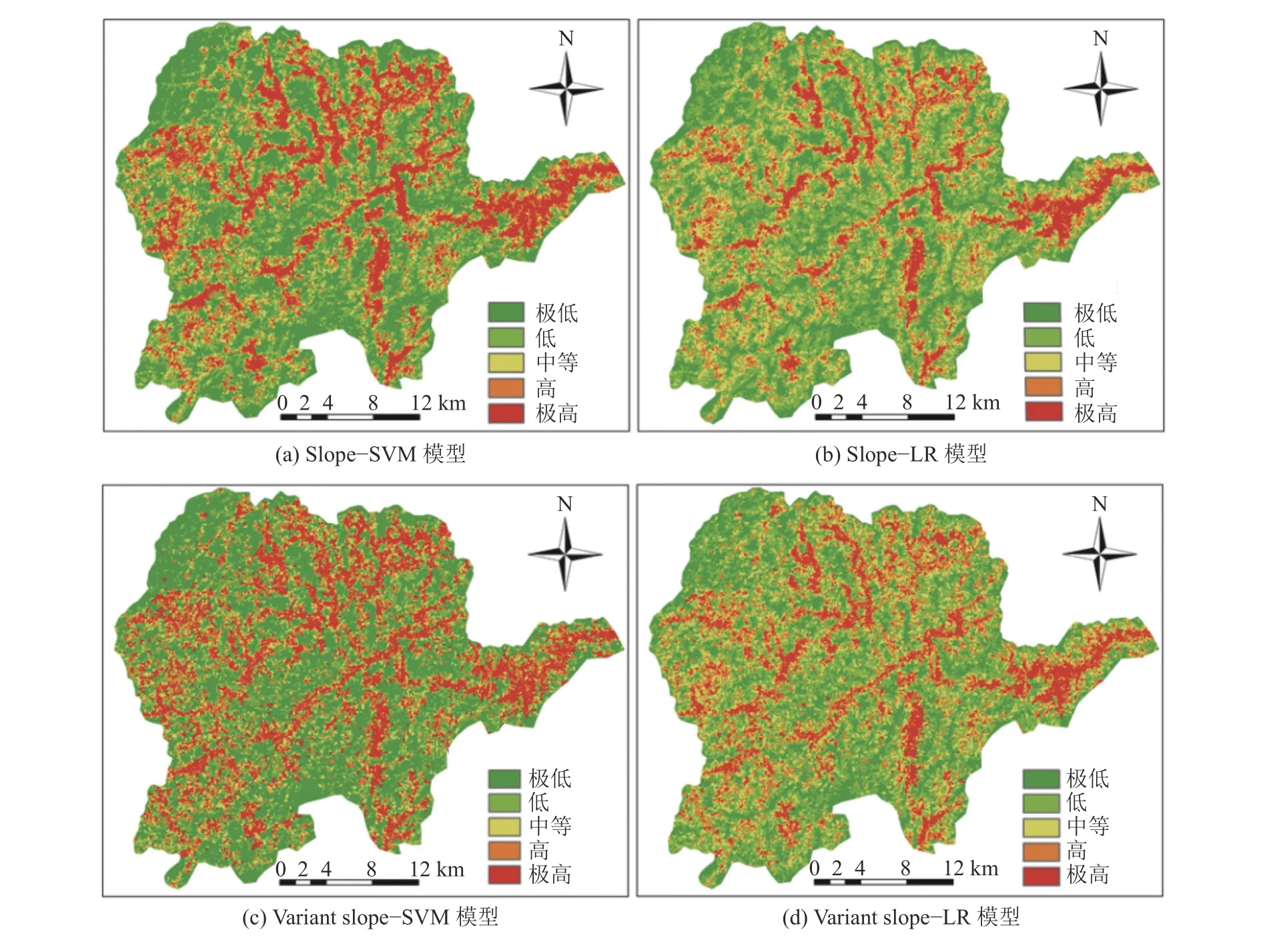
图8 不同预测模型的易发性分布Fig. 8 Landslide susceptibility distribution of different landslide susceptibility models

3.4 精度评价

3.4.1 ROC精度评价

ROC曲线是目前用于评估机器学习模型易发性预测性能最常用的方法，主要采用训练集和测试集样本中的预测概率和标签数据，以1–特异性为横坐标，敏感度为纵坐标绘制而成。ROC曲线下部面积（AUC）可以作为滑坡易发性预测精度[32]。

不同易发性评价模型的ROC曲线如图9所示。由图9可知，Slope–SVM、Variant slope–SVM、Slope–LR和Variant slope–LR模型的预测精度分别为0.812、0.876、0.818和0.839。图9结果表明无论是SVM模型还是LR模型，考虑斜坡单元内部非均质性的易发性结果的预测精度要高于基于斜坡单元的易发性结果。

图9 不同易发性预测模型的ROC曲线分布Fig. 9 ROC curves of different landslide susceptibility models

3.4.2 频率比精度

频率比精度是评估模型预测精度的另外一种有效的方法，该方法分别计算每个易发性等级下的斜坡单元占比和滑坡斜坡单元占比，二者的比值为该易发性等级的频率比[7]。不同易发性预测模型的频率比精度分布如图10所示。图10显示出各个易发性等级的频率比值从极高到极低等级逐渐降低。Slope–SVM、Variant slope–SVM、Slope–LR和Variant slope–LR模型的频率比精度分别为0.780、0.866、0.792和0.865。图10的结果表明考虑斜坡单元内部非均质性的易发性结果的预测精度要高于基于斜坡单元的易发性结果。

图10 不同易发性预测模型的频率比精度分布Fig. 10 FR accuracy values of landslide susceptibility classes for different landslide susceptibility models

4 讨 论

4.1 MSS单元划分方法的优点和不足

传统的水文分析法是根据地貌特征把斜坡单元定义为山脊线和山谷线之间的区域。虽然该定义的应用较广，实际意义较强，但是该方法仍存在很多缺陷。例如：水文方法划分的斜坡单元比较适用于地形地貌相对单一的地区，在地形地貌复杂的地区，水文分析法划分的斜坡单元往往包含多个斜坡或者是一个流域；该方法的参数设置主观性强，地域差别大；并且该方法效率低，不利于大区域尺度和高精度数据的斜坡单元的划分，划分斜坡单元的过程中出现大量不合理的长条状面，需要后期大量的人工调整。因此，水文分析法划分的斜坡单元应用性较弱。

相比于水文分析法，MSS方法将斜坡单元定义为一些内部坡向非均质性最小，外部坡向非均质性最大的对象单元。该方法可以实现大区域尺度和高精度数据的斜坡单元的自动划分，极大地提高了斜坡单元划分的效率。采用修正试错法可以更快更客观地确定该方法中的参数组合。该方法的实用推广性更强，适用于比较复杂的地形地貌区域，也适用于各类地质灾害的预测。因此，与传统的水文分析法相比，本文提出的MSS方法在斜坡单元的定义、参数设置、效率及应用推广方面都有一定的优势。但是，MSS方法仍然存在一些不足，例如，MSS方法划分的斜坡单元的边界锯齿状比较多，不够光滑；对于一些平坦地区，由于没有坡向导致划分的斜坡单元存在误差。

4.2 基于斜坡单元易发性预测结果分析

通过与采用栅格单元进行易发性预测的结果相比[10,20]，发现采用斜坡单元的易发性结果实际意义和应用性更强。选择斜坡单元作为易发性评价的基本单元，可以避免采用栅格单元结果中极高易发性区域过度聚集的情况，也避免因为数据精度差异和机器学习模型的不同导致的易发性图的差异。水文分析法提取斜坡单元的易发性结果对比发现，基于MSS方法提取斜坡单元的易发性结果更合理，避免了水文分析法斜坡单元面积过大导致评价结果过于零散的现象。此外，还可以准确地确定具有极高易发性的斜坡单元的位置，为防灾减灾工作者提供更加精确的结果。同时，采用斜坡单元的另外一个优势是可以充分地挖掘和分析斜坡单元内部环境因子之间的相关性和非均质性。Variant Slope–SVM/LR和Slope–SVM/LR模型的易发性结果的对比分析表明，考虑斜坡单元内部环境因子的非均质性可以提高易发性的预测精度。

5 结 论

本研究以江西省崇义县为例，采用MSS方法划分斜坡单元，考虑斜坡单元内部环境因子的非均质性，采用SVM和LR机器学习模型进行了易发性预测。研究结果表明：

1）与传统的水文分析法相比，MSS方法可以实现大区域内斜坡单元地快速自动划分，并且修正试错法可以更好地确定MSS方法的最优参数组合。当尺度、形状特征权重和紧致度权重参数取20、0.8和0.8时，崇义县斜坡单元的划分效果最好。

2）Variant slope–SVM/LR模型的ROC和频率比精度均显著高于Slope–SVM/LR模型，表明斜坡单元内部环境因子的非均质性可以用平均值、变化值和标准差3个变量来表征，考虑斜坡单元内部环境因子的非均质性可以充分地挖掘滑坡与环境因子之间的关系，使易发性预测结果更准确。

3）虽然MSS方法可以实现自动提取斜坡单元，但在未来的研究工作中，提取的斜坡单元形态仍需进一步的优化。另外，在滑坡易发性的评价过程中，应当充分挖掘研究区域历史滑坡的形态和空间分布特征。