新冠疫情前后人民币汇率的影响因素分析

黄思颖

(华南师范大学数学科学学院 广东广州 510631)

由于国内与国际经济形势的不断变化，人民币汇率也在不断波动。2010年6月，我国宣布继续汇率制度改革后，人民币出现明显升值，而2015年8月我国进行下一轮汇改时，人民币出现了贬值，汇率上升。直至2019年末新冠疫情爆发后，人民币又开始出现小幅度升值，汇率下降。

2010年1月—2021年11月的人民币汇率波动情况如图1所示。

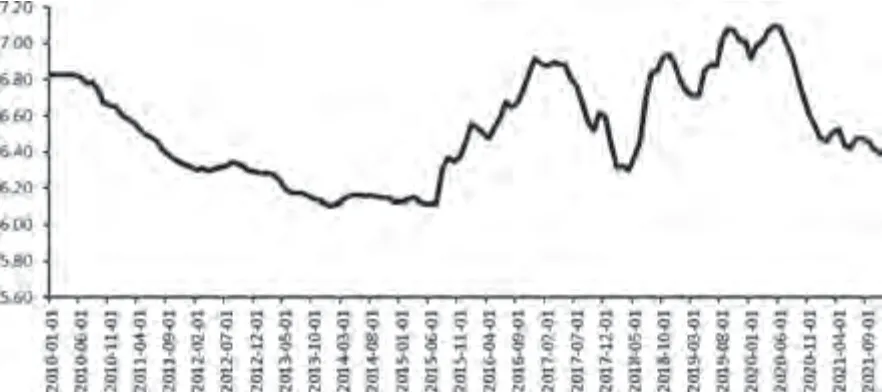
图1 人民币汇率波动情况

人民币汇率是衡量我国经济实力的重要指标，若人民币发生贬值，会使我国国内经济形势面临很大压力。关于人民币汇率的影响因素分析，国内很多学者使用不同的模型做过相应的研究，但其方法大部分为基础的计量经济学模型。例如，李浩宁(2021)使用VAR模型探究了人民币汇率的影响因素；李禧龙(2021)使用多元线性回归讨论了人民币汇率的影响因素。

目前，探究新冠疫情发生前后人民币汇率影响因素变化的文献不多，故本文为了探究各变量对人民币汇率的影响，采用RT方法对变量重要性进行分析，依此建立了加入新冠疫情影响前后的多元线性回归模型。

1 数据准备

本文选取货币供应量(x1)、中国制造业采购经理人指数(x2)、国家外汇储备(x3)、中美利差(x4)、中美CPI差值(x5)作为变量研究人民币汇率(k)变动的影响因素。选取的数据为2014年1月—2021年11月的月度数据，本文的所有相关数据均来自choice金融终端。由于货币供应量和国家外汇储备的数据较大，为了防止回归时产生较大误差，对原始数据进行了取自然对数的处理。

2 模型建立与分析

2.1 OLS回归

为了初步查看回归效果，本文建立多元线性回归模型研究人民币汇率的影响因素，建立的初始模型如下：

对数据进行OLS回归，得到的回归结果为：

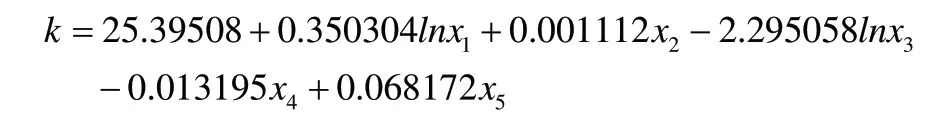
该模型的R2=0.807669，F=74.74886＞F0.05(5,89)=2.317，故认为人民币汇率与上述变量间总体线性关系显著。但其中，x2、x5前的参数估计值未能通过t检验，说明模型中存在问题，因此需要再对模型进行检验与改进。

2.2 多重共线性检验与逐步回归

2.2.1 相关系数热力图

由前文的初步分析可以猜测，模型存在多重共线性问题，因此需要对模型进行多重共线性检验，本文计算得出各解释变量间的皮尔逊相关性热力图如图2所示。

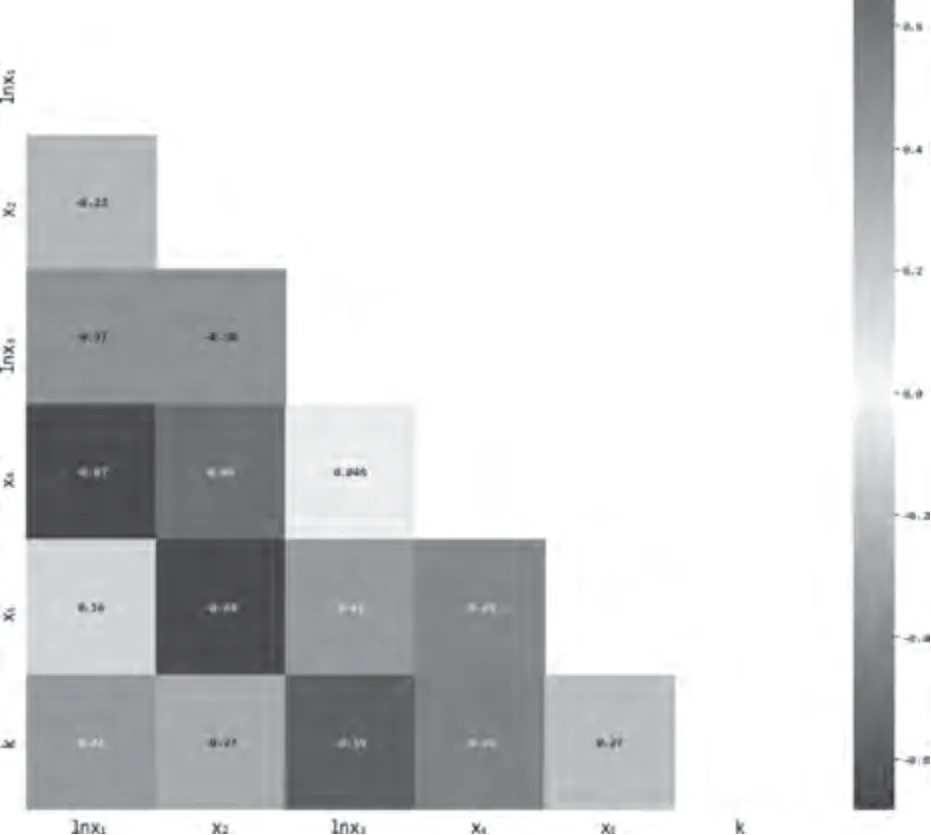
图2 相关性热力图

由此可以发现，货币供应量和中美利差、PMI与中美利差、PMI与CPI差值等变量之间的相关系数比较大，因此该模型存在多重共线性，具体还需进一步检验。

2.2.2 变量重要性分析

本文采用机器学习方法中的集成学习回归方法对各变量的特征重要性进行分析，从而更加客观判断各变量的重要性，利用RT进行回归学习，为变量重要性得分创建条形图以直观观测(见图3)。

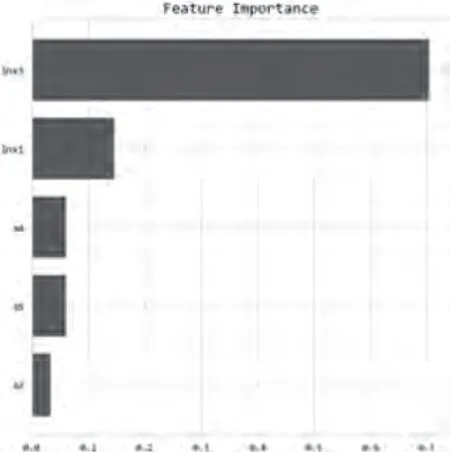
图3 RT方法计算变量重要性条形图

由图3可以发现，lnx3对y的影响最大，且显著大于其他变量，也就是说，国家外汇储备对人民币汇率的影响程度最大。其次是货币供应量、中美利差、CPI差值及PMI，且PMI对人民币汇率的影响显著小于其他变量。

2.2.3 逐步回归

由于本文所选的变量在很大程度上可能存在多重共线性，因此采用逐步回归的方式构建回归模型。

考虑到国家外汇储备对汇率的重要影响，本文考虑先保留lnx3，再逐个加入其他变量进行逐步回归。保留lnx3时，其回归函数为：

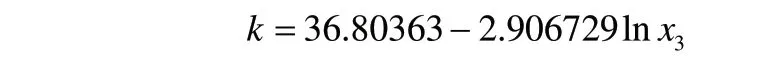
其R2=0.681289，F=198.8002，可见国家外汇储备对人民币汇率的解释力度很大，结合前文变量重要性的分析，显然可以确定该变量不能删除。

因此，依据逐步回归的思想，在固定保留lnx3的基础上，逐个加入其他变量，发现加入x5，即中美CPI差值时效果最佳，其R2上升为0.780291，回归函数为：

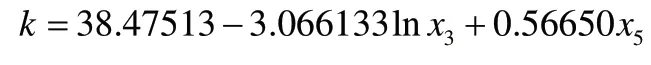
结合前文变量重要性的分析，可以说明中美CPI差值对人民币汇率的影响较大，且加入模型后不会出现多重共线性的现象。

因此，本文保留x5，在此基础上逐个加入其他变量，发现加入lnx1，即货币供应量时效果最佳，其R2上升为0.806719，回归函数为：

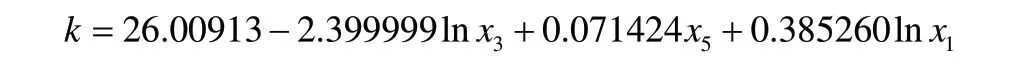
因此，在原有模型的基础上增加lnx1变量，可以增加模型的解释力，且不会出现多重共线性问题。

此时，若再引入其他变量，模型的解释效果会下降，且变量无法通过t检验。这说明在本文所选的五个变量中，lnx1、lnx3以及x5就可以对人民币汇率k有很强的解释力，且变量之间不会存在多重共线性。综上所述，此时该模型拟合结果最佳：

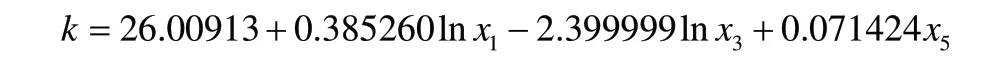
2.3 异方差性检验与修正

除了去除多重共线性的干扰之外，还需要对该模型进行异方差检验，避免模型出现异方差性，从而影响模型的评估效果。

因此，本文采用eviews7.2进行检验，其检验结果如图4所示。

图4 怀特检验结果

显然，在检验结果中，0.0385＜0.05，故可以认为模型存在异方差性，因此需要对异方差性进行修正。本文采用加权最小二乘法以提高参数估计的精度。

为了选取效果最好的权数进行加权最小二乘法，本文通过了很多尝试，最终选择了

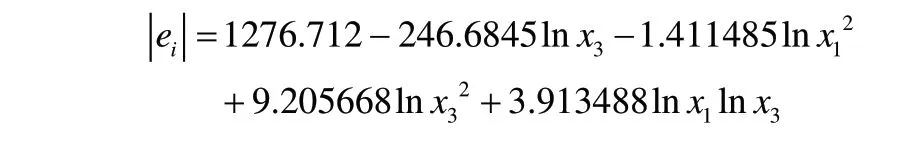
作为权数进行加权回归，其回归结果为：

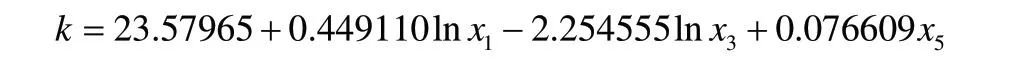
此时的R2上升为0.861269，F=188.3153，说明该模型的拟合效果很好。此时再对该模型进行怀特检验，其P值为0.3665＞0.05，已经不存在异方差性。因此，本文最终建立的多元线性回归模型为：

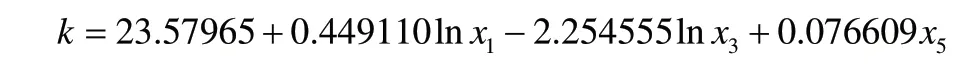
综上，在该模型中，最终仅保留了货币供应量、国家外汇储备及CPI差值三个变量。从模型效果可以发现，这三个变量可以对人民币汇率进行较好的解释说明，且该模型满足普通最小二乘回归的基本假设，对被解释变量有很好的解释度。

3 考虑新冠疫情影响的模型

3.1 变量重要性变化分析

为了考虑新冠疫情对国家汇率的影响，本文将2020年开始的数据进行分析，绘制变量重要性条形图(见图5)。

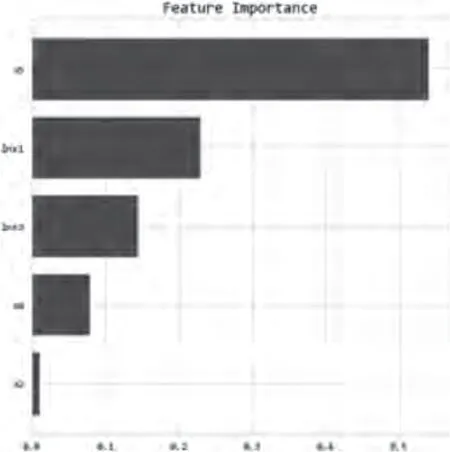
图5 RT方法计算变量重要性条形图

显然，在这种情况下，各变量对人民币汇率的影响程度有了很大改变，可以说明在新冠疫情爆发后，各变量的重要程度也相应发生改变。

3.2 加入虚拟变量的OLS回归

为了解新冠疫情对模型的影响，本文引入虚拟变量D。2020—2021年的数据中，令D=1；2014—2019的数据中，令D=0。

由于lnx3依旧是重要变量之一，本文同样选择优先保留lnx3，再逐个加入解释变量，按照与前文同样的方法进行逐步回归，再同样进行异方差检验，可得到其P值为0.0497＜0.05，可以说明该模型不存在异方差。因此，该模型的最终回归方程为：

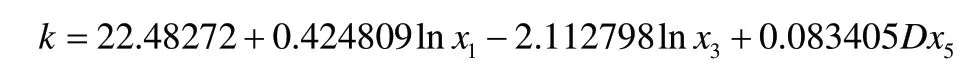
观察结果可以发现，斜率差异系数在统计意义下为显著，说明在2019年末新冠疫情爆发之后中美CPI差值对人民币汇率的影响机制发生了明显的变化。在2019年末，其他条件不变的情况下，中美CPI差值每增加1%，人民币汇率比2019年之前多增长0.006796。

4 结语

综上所述，货币供应量、国家外汇储备及中美CPI差值这三个变量都对人民币汇率具有显著的影响。其中，货币供应量与人民币汇率呈正相关关系，国家外汇储备与人民币汇率呈负相关关系，而中美CPI差值与人民币汇率呈正相关关系。

在新冠疫情爆发之后，以2019年为节点，中美CPI差值对人民币汇率的影响机制有所改变，各个指标的重要性也有所不同，且整体来看，人民币汇率有所下降，即人民币出现升值的趋势。

根据结论进一步完善外汇储备的管理制度，合理对外汇储备进行管理及建立健全的货币政策，使国家外汇储备、货币供应量及CPI处于较为合理的水平，对维持人民币汇率的稳定具有重要意义。