二维半导体莫尔超晶格中随位置与动量变化的层间耦合*

郭瑞平 俞弘毅2)†

1) (中山大学物理与天文学院,广东省量子精密测量与传感重点实验室,珠海 519082)

2) (中山大学,光电材料与技术国家重点实验室,广州 510275)

近些年来引起广泛关注的二维半导体莫尔超晶格系统中存在着莫尔激子、强关联电子态和面外铁电性等新奇物理现象,电子的层间耦合对于理解这些现象至关重要.本文研究了二维半导体双层莫尔超晶格中的层间耦合随位置和动量的变化.外势场导致的局域布洛赫波包的层间耦合与波包宽度以及中心位置处的层间平移有着密切关系.同时,层间耦合随动量的变化使得基态 S 型波包和激发态 P± 型波包有着截然不同的随中心位置变化的层间耦合形式: 在两个 S 型波包的层间耦合消失的位置,S 和 P+ 型(或 S 和 P− 型)波包之间的层间耦合达到最强.利用该性质,可以通过外加光电场来调控特定谷的基态波包的层间输运.此外,双层系统中发现的面外铁电性可以归结为不同层导带和价带间的耦合导致的电子在两层中的再分配现象.将本文得到的层间耦合形式与单层紧束缚模型相结合,可计算出垂直平面的电偶极密度,其随层间平移的变化形式和数量级与实验观测相符.

1 引言

近10 年来,过渡金属硫族化合物(transitionmetal dichalcogenides,TMDs)这种二维材料因其在下一代光电技术中的应用潜力而受到了物理、化学和材料等研究领域的高度关注[1−3].TMDs(包括MoS2,MoSe2,MoTe2,WS2和WSe2)、六方氮化硼(hexagonal boron nitride,hBN)和石墨烯均为具有层状结构的二维材料,每一个单层为共价键组成的六角晶格,而层与层之间则以较弱的范德瓦耳斯力结合.当前用于获得单层二维材料的技术,包括机械剥离、化学气相沉积和分子束外延生长法,已经发展得比较成熟.单层极限下,这些二维材料在费米面附近的能带边均位于六角布里渊区能量简并但不等价的两个角落±K,称为谷赝自旋[4].但与先前已经受到广泛关注的石墨烯不同,单层TMDs 是直接能隙位于红外到可见光波段的半导体,因此非常适合光电和半导体光学相关的应用器件[1−3].此外,过渡金属的强自旋轨道耦合效应使得TMDs 的±K谷价带(导带)携带符号相反、大小在0.15—0.40(0.03) eV 的自旋劈裂,导致了带边附近谷赝自旋和自旋的一一对应[5]: 如果能量最低的位于 +K谷的空穴具有向下的自旋,那么具有相同能量的位于−K谷的空穴具有向上的自旋.这也使TMDs 成为设计制造自旋/谷电子学器件的理想平台之一.

将两个单层系统上下堆叠得到的范德瓦耳斯双层结构可极大地扩展二维层状材料在研究和应用上的前景[6].与单层TMDs 相比,相邻层之间的层间耦合效应带来了双层TMDs 中更为丰富的可调控性和新奇物理现象,尤其是当双层系统中存在莫尔超晶格时[7,8].莫尔超晶格出现在两层材料的晶格常数非常接近而且晶格朝向几乎一致时,其周期通常在几纳米到十几纳米之间,远大于单层材料的晶格常数(3 Å左右).在一个超原胞内的不同位置,层间耦合随不同层原子的上下堆叠方式的改变而缓慢变化[9],导致层间距、超晶格势、光学属性和层赝自旋等众多物理性质随位置的变化[10−15].这进一步导致例如莫尔激子[16−21]、强关联多体电子态[22−33]和垂直平面的铁电性[34−42]等实验现象.为了理解这些新奇物理现象背后的物理机制,有必要在先前已有的结论上[9],对二维层状半导体材料中层间耦合的形式进行更深入的分析和讨论.

本文从单层TMDs 的电子布洛赫波本征态出发,推导了双层TMDs 莫尔超晶格中的层间耦合随位置和动量的变化.通过分析发现,非局域的布洛赫波和局域的布洛赫波包的层间耦合随位置和动量的变化可导致莫尔超晶格势的出现以及电子在不同层的再分配,这也是很多实验现象背后的物理机制.本文内容简述如下: 第2 节是关于晶格匹配或不匹配的双层系统中非局域化的布洛赫波之间的层间耦合;以此为基础,第3 节给出了莫尔超晶格中局域化的布洛赫波包之间的层间耦合形式,并将其与晶格匹配的双层结构中的布洛赫波层间耦合做了对比;第4 节讨论了近期实验上观测到的双层系统中的垂直平面电偶极矩,它可被层间耦合导致的电子在不同层的再分配现象很好地解释;第5 节对全文做了总结,并讨论了采用的研究方法的局限性.

2 非局域化的布洛赫波之间的层间耦合形式

2.1 单层材料中的电子布洛赫函数

对于TMDs、hBN 和石墨烯这些二维层状材料,同一层内部的原子之间是通过共价键结合,而不同层之间则是以较弱的范德瓦耳斯键结合.因此通常采用的处理方法是以单层材料的电子布洛赫函数为出发点,将层与层之间的耦合效应看作微扰.单层TMDs 中电子的哈密顿量为

等号右边第二项代表单层TMDs 的周期晶格势,R是过渡金属原子M 在二维平面上的位置.该哈密顿量的本征态为单层布洛赫函数ψn,k(r),其中n为能带指标,k为晶格动量.ψn,k(r) 可以展开成以下原子轨道线性组合的布洛赫和形式:

其中N是系统总的原胞数目,Dn,k(r −R) 是局域在R附近的原子轨道线性组合,其组合方式随n和k而变化.

上述结果利用了eiq·(r−R)dm(r −R)≈dm(r −R)的性质(m=0,±2),这是因为|q|≪|K|,而且dm(r −R)是一个高度局域化的原子轨道,其绝对值随|r −R|指数衰减.

2.2 双层材料中不同层布洛赫函数之间的层间耦合

从(2)式的单层TMDs 布洛赫函数出发,可推导出不同层布洛赫函数之间的层间耦合形式.双层TMDs 系统中的电子哈密顿量为

3 局域化的布洛赫波包之间的层间耦合形式

本节从局域的角度来看待莫尔超晶格中的电子.图2(a)所示为一个典型的莫尔超晶格以及对应的超原胞,其周期λ通常在几纳米到十几纳米,远大于单层TMDs 的晶格常数a ≈3 Å.在一个范围小于λ同时又大于a的局部区域内,双层TMDs的原子排布方式与一个晶格匹配的双层结构几乎相同(见图2(a)).如果有一个局域在该区域的电子波包,直觉上其性质应与某个特定层间平移下的晶格匹配双层结构中的电子接近,这正是文献[11−15]采用的处理方法.需指出的是,层间平移在晶格匹配的双层TMDs 中为一不随位置变化的常数,而在莫尔超晶格中则随位置缓慢变化.如图2(b)所示,坐标原点处的层间平移r0与位置Rc=处的层间平移r0(Rc) 之间满足[11]r0(Rc)=r0+R −Rc,这里r0+R=r0+l1a1+l2a2是R′附近下层TMDs 中某个金属原子位置.于是

图2 莫尔超晶格中局域化的布洛赫波包之间的层间耦合 (a) 层间转角接近0°下周期为 λ 的莫尔超晶格示意图,菱形为一个超原胞,A,B,C为三个范围小于λ同时又大于单层晶格常数a 的局部区域,其内部的原子排布与层间平移分别为r0(A)=0,r0(B)=(a1+a2)/3 和 r0(C)=2(a1+a2)/3 的晶格匹配的双层结构 接近.(b) 层间平移 r0(Rc) 随区域中心位置 Rc 的变化,其满足 r0(Rc)=r0+R −Rc .(c) 通过外场调控两个局域在 B 处的 S 型波包之间的层间耦合,其中黑色直线箭头代表与 S 型波包有关的非零层间耦合,红(蓝)色波浪箭头代表用 σ+ (σ−)圆偏振光场实现同一层内部的 S 型到 P+ (P−)型波包的激发.上下层波包的相对能量可通过施加层间电压来调节.(d) 在双层系统中,可通过施加 σ+ 圆偏振光将下层中 −K 谷的S型波包通过层间跃迁移动到上层,而 +K 谷则被留在下层.波包的局域化来源于上下层接触区域形成的莫尔超晶格势,我们设下层感受到的势阱较深因此基态波包无法自由运动,而上层感受到的势阱较浅因此基态波包可在层内运动,它们在一个面内电场的作用下可产生谷流Fig.2.The interlayer coupling between two localized Bloch wavepackets in the moiré superlattice.(a) Schematic illustration of a moiré superlattice with a period λ when the twist angle is close to 0°.The diamond shape corresponds to a supercell.A,B and Care three local regions with spatial extensions smaller than λ but larger than the monolayer lattice constant (a),whose atomic registrations are close to lattice-matched bilayer structures with interlayer translations r0(A)=0 ,r0(B)=(a1+a2)/3 and r0(C)=2(a1+a2)/3,respectively.(b) The variation of the interlayer translation r0(Rc) with the local region center Rc,which satisfies r0(Rc)=r0+R −Rc .(c) Tuning the interlayer coupling between two S -type wavepackets localized at B with external fields.Black straight arrows indicate the nonzero interlayer couplings related to the S -type wavepackets,while red (blue)wavy arrows stand for σ+ (σ−) circularly-polarized optical fields which can excite an S -type to a P+ -type (P− -type) wavepacket.The relative energy position between the upper-and lower-layer wavepackets can be tuned by an interlayer bias.(d) A schematic illustration of how to move th e −K valley S -type wavepackets from the lower-to upper-layer by applying a σ+ circularly-polarized optical field.Meanwhile the +K valley wavepackets remain in the lower-layer.The wavepacket is localized by the moiré potential at the region where two layers are in contact.We assume that the carriers in the lower-layer feel deep potential wells thus cannot move,while those in the upper-layer feel shallow potential wells thus can move under the effect of an in-plane electric field,which results in a valley current.

下文从波包的函数形式出发结合第2 节得到的布洛赫波之间的层间耦合((12)式),来推导不同层的布洛赫波包之间的层间耦合,并分析其与(13)式的异同.考虑一外势场导致的电子局域化,这样的势场可以来源于扫描隧穿显微镜的探针或是杂质电荷等.将势场近似为二维简谐势,于是电子基态为 S 型高斯波包,而第一激发态为 P±型高斯波包,它们在下层TMDs 中的波函数分别为

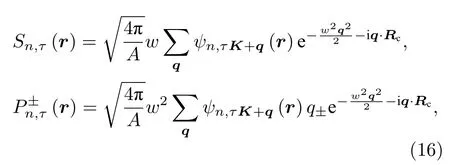
其中w是波包在实空间的展宽,A是双层TMDs系统的面积,Rc为外势场的最低位置或波包中心.波包在动量空间的分布中心则位于布洛赫函数的能量极值点τK.对于上层TMDs 中展宽为w′的波包,其波函数可类似写出.以一对谷赝自旋为τ=τ′=+(R 类堆叠)或τ=−τ′=+(H 类堆叠)的价带电子为例,利用(12)式和(15)式可得两个基态 S 型波包之间的层间耦合形式:

此外,两个布洛赫态的层间耦合中的q一阶项(见(12)式)使得 S 型和 P±型波包之间也存在有限大小的层间耦合:

由(18)式可以看出,S型到P±型波包之间的层间耦合强度随展宽w或w′的减小而迅速增大,而且它随r0(Rc) 的变化与两个 S 型波包的情况完全不同.由图1(c)可知,当选择波包中心Rc使得两个 S 型波包的层间耦合最强时,S 和P±型波包之间的层间耦合必然为0;反之如果将Rc选在两个 S 型波包的层间耦合为0 的位置,那么必然有 S 和P+型(或 S 和 P−型)波包之间的层间耦合达到最强.波包之间的层间耦合为0 或最强的情况往往出现在具有对称性的区域,即图2(a)中的A,B或C,在这些位置上下层的旋转中心在面内重合.局域在A,B或C的 S 和 P±型波包同样满足对称性,其C3量子数包括来自布洛赫函数ψn,τK和波包的包络两部分的贡献.需要注意的是,ψn,τK的C3量子数与旋转中心的选择M,X 或h 相关(见表1),当固定上层TMDs 的旋转中心为M'时,与之重合的下层旋转中心在A,B或C分别为M,h 和X.相应的波包C3量子数总结列于表2,显然,只有在上下层的波包具有相同C3量子数时,它们之间的层间耦合才不为0.

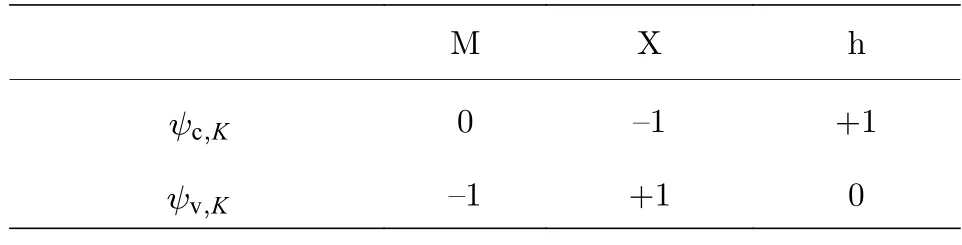
表1 导带和价带布洛赫函数在K 点的C3 量子数在不同旋转中心下的取值,其中M 为过渡金属,X 为硫族原子,h 为M 和X 组成的正六边形中心Table 1.The C3 quantum numbers of the conduction and valence band Bloch functions at K for different rotation centers.Here M is the transition-metal site,X is the chalcogen site,and h is the hollow center of the hexagon formed by M and X.

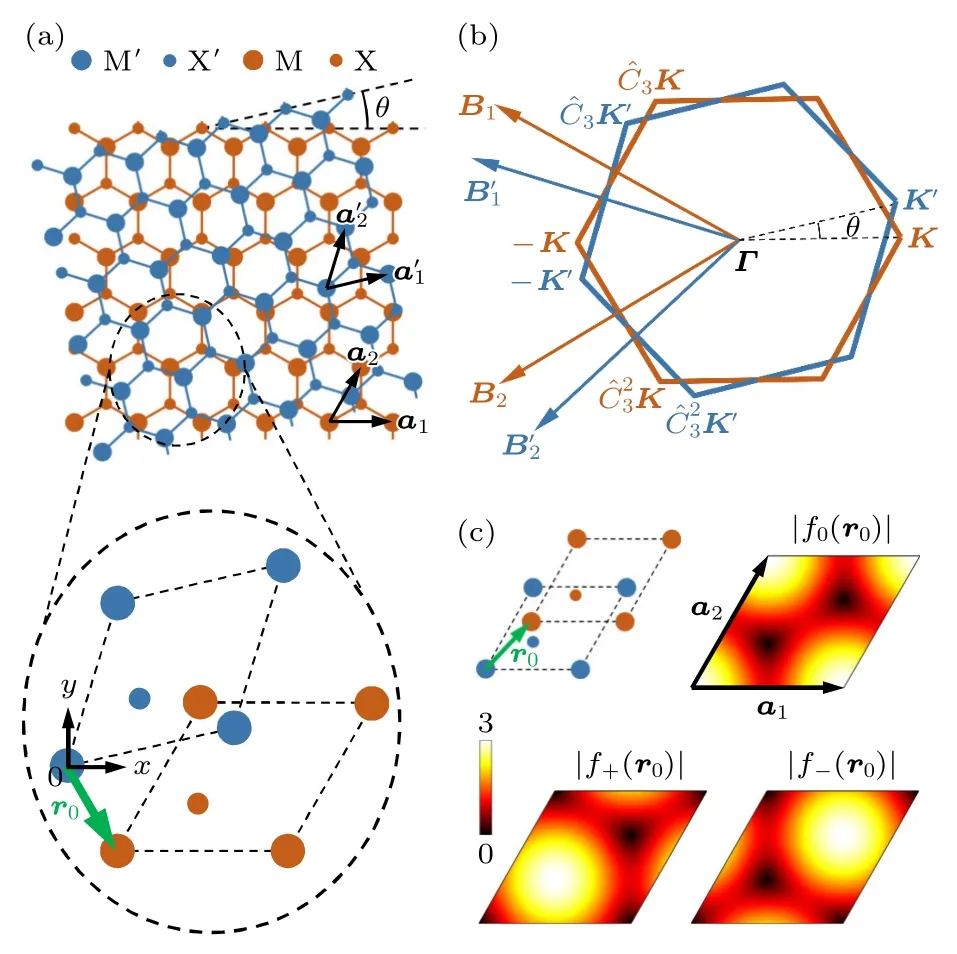
图1 双层TMDs 中布洛赫电子之间的层间耦合 (a)层间转角为 θ 的双层TMDs 示意图,其中蓝(橙)色大圆圈代表上(下)层的过渡金属原子M′ (M),蓝(橙)色小圆圈代表上(下)层的硫族原子X′ (X);下半部分为局部放大后得到的不同层的原胞,平面坐标原点选在上层的某个过渡金属原子上;(b)上下层的六角布里渊区示意图;(c)在两层TMDs 晶格完全匹配的情况下,(14)式中的 |f0(r0)|,|f+(r0)| 和 |f−(r0)| 随层间平移 r0的变化Fig.1.Interlayer coupling in bilayer TMDs: (a) Schematic illustration of a bilayer TMDs with a twist angle θ,where large blue (orange) circles stand for the transition-metal atoms M′ (M) in the upper (lower) layer,small blue (orange) circles are the chalcogen atoms X′ (X) in the upper(lower) layer.The lower part indicates an enlarged view of unit cells in two layers.The xy -coordinate origin is set on a transition-metal atom of the upper layer,and a nearby transition-metal atom in the lower layer has the spatial coordinate r0 .(b) The upper-and lower-layer Brillouin zon es.(c) The values of |f0(r0)| ,|f+(r0)| and |f−(r0)|in Eq.(14) as functions of r0 when the two TMDs lattices are fully commensurate.

上述性质使得两个 S 型波包之间的层间耦合可以通过外场来调控.在晶格匹配的R 类双层TMDs 中,最稳定的3R结构对应于层间平移r0=(a1+a2)/3或 2(a1+a2)/3 ;而在接近0°转角的双层TMDs 莫尔超晶格中,±K谷的空穴感受到一个莫尔超晶格势,其势能的最低点也是出现在层间平移r0(B)=(a1+a2)/3 或者r0(C)=2(a1+a2)/3的高对称位置[14,15,47](见图2(a)).在价带边位于±K的双层WSe2中[48],考虑被局域在B处的空穴波包,根据表2 的对称性知

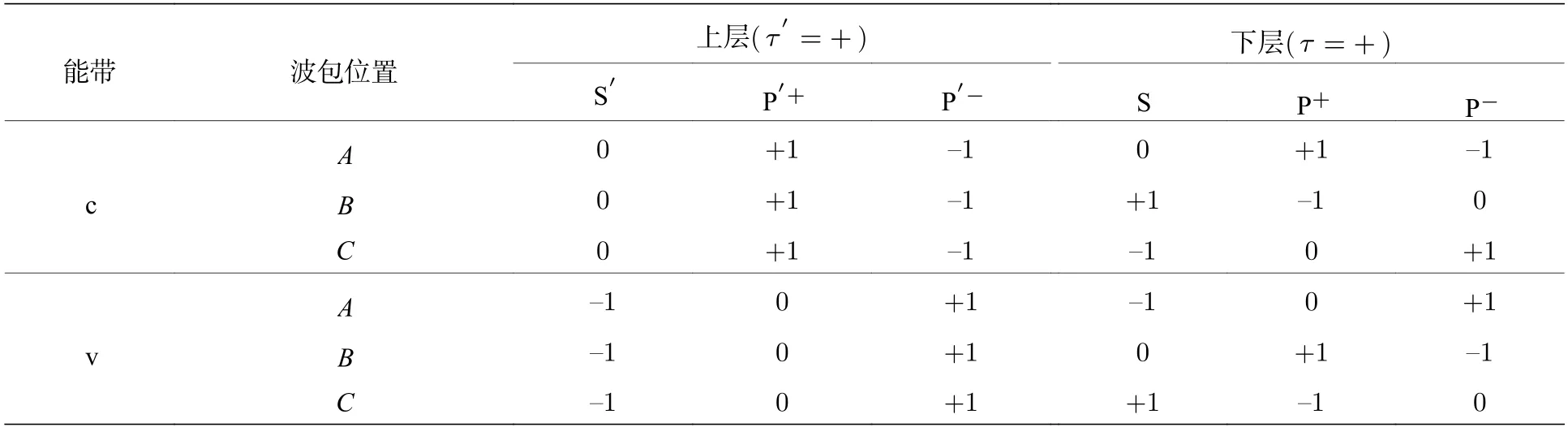
表2 局域在图2(a)中 A,B 和 C 区域的 S 和 P± 型波包的 C3 量子数,其中旋转中心始终取为上层TMDs 晶格的过渡金属M′.这里只显示了谷指标为τ=+和 τ′=+的情况,而 τ=− 和 τ′=− 可通过时间反演得到Table 2.The C3 quantum numbers of S -and P± -type wavepackets localized at A,B and C in Fig.2(a).Here we set the rotation center as a transition-metal site M′ in the upper TMDs layer.Only those with the valley indices τ=+and τ′=+are shown,while the cases for τ=− and τ′=− can be obtained by a time reversal.

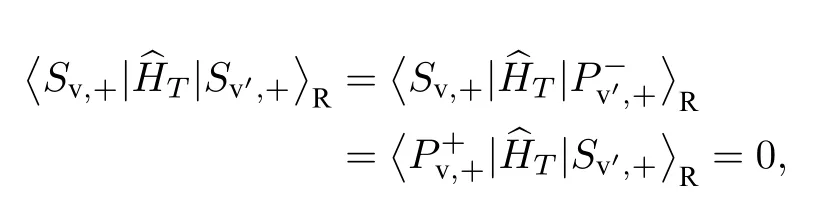
4 层间耦合导致的电子在不同层的再分配

层间耦合效应的另一个效果是导致基态电子在两层中的不平衡分布,从而在每一层中产生非零净电荷密度.如图3(a)所示,半导体TMDs 或绝缘体hBN 的费米面EF位于导带和价带之间的能隙中,因此两层的价带均被电子占据而导带均无占据.引入层极化算符其期望值对应从上层转移到下层的电子数.当不存在层间耦合时,所有被占据电子的基态|Ψ〉由低于费米面的ψn,k和ψn′,k组成,此时=0,即不存在电子的层间转移.当引入层间耦合效应时,为简单起见我们只考虑导带和价带: 下层的价带 v 和上层的导带 c′之间存在层间耦合而下层的导带 c 和上层的价带 v′之间存在层间耦合它们带来的层间杂化可产生有限大小的电子层间转移;另一方面上下层的价带都被电子占满(导带上无电子占据),因此价带之间(和导带之间)的层间耦合不会导致电子层间转移,可不考虑.通常层间耦合的强度远远小于能隙,二阶微扰下价带波函数变为

图3 电子在层间的再分配效应 (a)双层半导体TMDs 或绝缘体hBN 的费米面 EF 示意图;(b)单层hBN 的pz 轨道紧束缚能带,插图中 ∆R1,2,3 是hBN 晶格的3 个最近邻位移矢量,t 是最近邻跃迁强度;(c)计算得到的双层hBN 层极化密度随层间平移r0的变化;(d)三种不同r0 时的双层hBN 原子排布,上半部为上方视角,下半部为侧方视角,虚线箭头代表从N 向B 原子的电子转移,其中蓝(橙)色大圆圈代表上(下)层的N 原子,蓝(橙)色小圆圈代表上(下)层的B 原子Fig.3.The interlayer charge redistribution effect: (a) Diagram of the Fermi level EF of the bilayer semiconductor TMDs or insulator hBN;(b) the conduction and valence bands obtained from the pz-orbital tight-binding model for the monolayer hBN,in the inset,∆R1,2,3corresponds to the three nearest-neighbor displacement vectors,and t is the nearest-neighbor hopping;(c) the calculated layer-polarization density in bilayer hBN as a function of the interlayer translation r0 ;(d) the atomic registries of bilayer hBN under three different r0, the upper (lower) parts correspond to the top-view (side-view).The dashed arrows denote the electron redistribution from N to B atoms.Here the large blue (orange) circles stand for the N atoms in the upper (lower) layer,small blue (orange) circles are the B atoms in the upper (lower) layer.

双层hBN 的层间耦合形式与TMDs 类似.对于晶格匹配的R 类双层hBN,近似取不同层的两个原子的pz轨道之间的层间耦合形式为

于是可推导出导带和价带之间的层间耦合:

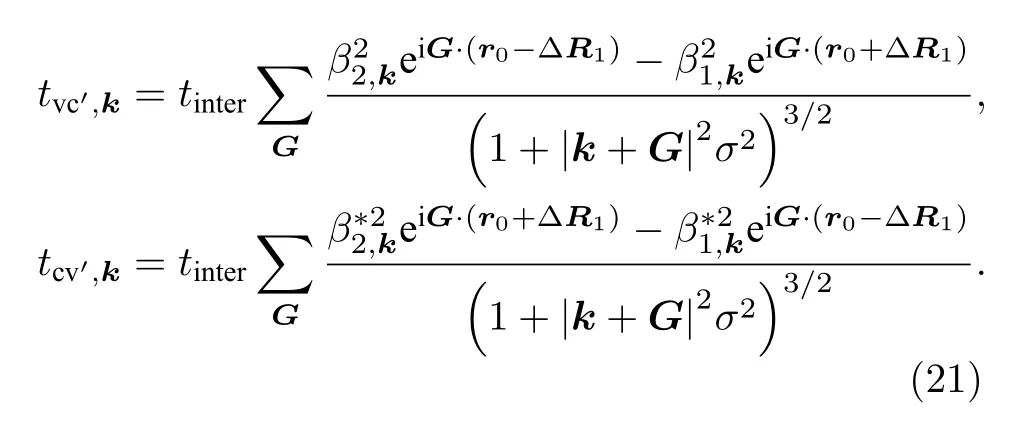
在层间跃迁参数tinter=0.6 eV,衰减特征长度σ=1 Å下,计算得到的层极化密度随r0的变化见图3(c).可以看到,r0=(a1+a2)/3 和2(a1+a2)/3时层极化最大且符号相反,它们恰好对应双层hBN最稳定的AB 和BA 两种构型;而r0=0 的AA 构型下,上下层互为镜像对称,层极化密度为0(见图3(d));其余r0下的层极化密度则取中间值.不同参数下,层极化密度的大小随之变化,但其随r0变化的函数形状基本固定.非零的层极化代表不同层中有非零且符号相反的净电荷密度,即存在一个垂直平面的电偶极矩.在莫尔超晶格中,r0(Rc)随位置Rc缓慢变化,因此不同区域有着不同的电偶极密度,这使得其中的电子和空穴感受到一个随位置变化的静电势,这正是莫尔超晶格势的主要来源[50].而莫尔超晶格势导致的局域化是莫尔激子[16−21]以及电子强关联多体态[22−33]出现的重要原因.电子的层间再分配导致的垂直平面电偶极矩已被多个实验在双层hBN 和TMDs 系统中观测到[34−42],且测得的电子数密度随r0的变化方式以及数量级(～0.01 nm–2)与这里采用的简单模型估算结果相符.

上述对电子层间再分配的讨论是基于单层布洛赫函数,但从直观的角度,它更易于理解的方式是电子在不同层的B 和N 原子轨道之间的转移[51].由于B 和N 原子具有不同的电子亲和势,当位于不同层的两者相互靠近时,N 原子上的电子会向B原子靠近以降低总能量,这会导致少量电子在两层中的再分配.层间距固定的情况下,不同层的N 向B原子转移的电子数随两者的面内距离指数衰减.如图3(d)所示,在r0=(a1+a2)/3 (r0=2(a1+a2)/3)时,上层的B(N)原子与下层的N(B)原子在面内的位置重叠,因此转移的电子数达到最大,这导致了一个垂直向下(上)的电偶极矩;而在r0=0时,上层的B(N)原子与下层的B(N)原子在面内重叠,上下层互为镜像对称,层间的净电荷转移为0.

5 总结与讨论

本文以单层二维半导体材料中的布洛赫态为出发点,给出了位于不同层中的布洛赫态层间耦合的具体形式,并着重分析其在带边±K附近与晶格动量的关系,以及局域布洛赫波包的层间耦合与其中心位置的关系.在双层莫尔超晶格中,布洛赫波包的性质随波包中心Rc处的层间平移r0(Rc) 剧烈变化,这使得不同位置处波包的层间耦合差异极大.同时,布洛赫态层间耦合随晶格动量的变化使得激发态P±型波包具有与基态 S 型完全不同的层间耦合形式,利用该性质可以用外场来选择性地打开或关闭特定谷的 S 型波包层间耦合,从而实现对谷的层间输运的调控.最后一节分析了层间耦合导致的电子在不同层的再分配,并用一个简单的紧束缚模型计算了产生的电偶极矩密度,给出的数量级与实验相符.这说明本文的结果可以用来分析层间耦合带来的实验现象,并用在基于双层材料新奇物理性质的器件上.

前面的分析将双层系统中的单层材料视为刚性,在该假设下r0(Rc) 为Rc的线性函数.但实际上在莫尔超晶格的周期很大时,每个单层中的原子排布都会发生细微的重构,导致r0(Rc) 不再是Rc的线性函数.但是本文关于波包的大部分结果仍成立,即波包的性质由其中心所在区域的r0(Rc) 决定,只是它随Rc的函数关系会发生改变;同时在A,B和C区域,由对称性分析得到的结论(表2 和图2(c))也成立,只是层间耦合的定量大小会受到原子排布重构的影响.期望将来有更精确的分析原子排布重构影响下的层间耦合的结果.