双泡耦合声空化动力学过程模拟*

许龙 汪尧

1) (中国计量大学理学院,杭州 310018)

2) (中国计量大学,浙江省智能制造质量大数据溯源与应用重点实验室,杭州 310018)

为了对双泡耦合的声空化过程进行模拟,本文从流体动力学控制方程和流体体积分数模型出发,在Fluent 软件中构建双泡耦合超声空化三维有限元仿真模型,对超声波驱动下流体中双泡耦合声空化动力学过程进行数值模拟,并通过对空化气泡周围声场的变化进行分析研究双泡耦合声空化的非线性动力学特性.结果显示: 在超声波驱动下,球形气泡先缓慢扩张,扩张到最大半径后迅速收缩直至溃灭;耦合双气泡间存在相互作用力,使得空化气泡的扩张受到抑制、气泡收缩时间增长;空化气泡在收缩阶段的能量转换能力增强,相比单气泡声空化,耦合双气泡溃灭时气泡内部的压强更大.本文分析结果将为超声空化泡群的动力学过程模拟提供参考.

1 引言

超声空化通常是指液体中存在的微气泡在超声波的作用下振荡、生长、收缩和崩溃等一系列非线性动力学过程[1].1917 年,Rayleigh 提出Rayleigh气泡动力学模型之后,Plesset 等在此基础上提出了Rayleigh-Plesset 方程.此后大部分单泡和泡群径向脉动的理论研究都是考虑各种复杂情况时对Rayleigh-Plesset 方程进行修改[2].文献[3]利用高速摄影系统对气泡运动和泡群的分布进行了观察.文献[4]对超声波驱动下的泡群系统共振特性进行了研究.文献[5]提出了在考虑气泡耦合振动影响时球状泡群内气泡振动的动力学方程.文献[6] 对空化气泡振动特性的影响因素进行了研究.文献[7]研究了泡群中气泡之间的边界振动.文献[8]研究了空化气泡溃灭时间的影响因素.

以上关于空化泡的理论研究,大多数都是从空化泡进行理想的球形振荡出发,但实际研究中发现空化泡运动并不总是保持球形[9].2005 年,An 等[10]考虑非球形对称声压扰动对空化气泡的影响,对气泡的不稳定性相图进行了计算.Liang 等[11−13]于2012 年研究了球形声场环境中双气泡的非球形变形,2017 年和2021 年对非球形声场中双气泡的运动特性以及基于势流和微扰理论对超声场中双气泡的不稳定性进行了研究.马艳等[14]对双空化气泡之间相互作用力对气泡形状的影响进行了研究.Wu 等[15]使用高速摄像机观测了油水交界面处空化气泡的演化过程.但是仅凭借现有实验设备,很难对超声空化过程声场中各种变化进行精确观测.近年来,由于计算流体动力学(computational fluid dynamics,CFD)技术的快速发展,使得可以对超声空化过程中的空化气泡运动过程以及声场中各位置基本物理量(如速度、压力、温度等)的变化进行监测分析[16,17].文献[18]基于Fluent 软件环境,模拟了近壁面空化气泡溃灭过程.文献[19]提出了一种运用流体体积(VOF)方法追踪多个空化泡的运动界面的计算方法.文献[20]采用VOF 方法模拟了管道内空化泡的动力学特性.文献[21]对空化效果与超声频率之间的关系进行了分析.文献[22]将有限体积法和流体体积模型结合起来对近壁面微气泡的溃灭特性进行研究.之后还有许多学者对近壁面以及静态流场中空化泡的形变开展了研究[22].但是,对于在声场作用下微小空化泡的形状变化的研究却非常少.

本文建立了双气泡耦合超声空化的三维有限元仿真模型,基于Fluent 软件对超声波驱动下液体环境中双气泡耦合振动的非线性动力学过程进行模拟,研究超声空化过程中空化气泡形态变化与周围物理场变化的关系.该仿真模型将为后续超声空化泡群动力学过程模拟提供参考.

2 基本理论与仿真模型的建立

2.1 控制方程

对于超声空化过程中的数值模拟,有如下假设: 1)流体是非可压缩牛顿流体,并且以湍流形式流动;2)忽略重力因素;3)忽略体积力作用.

根据质量守恒定律,质量的连续方程为[17]

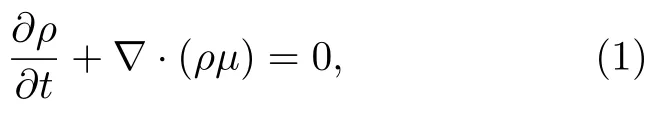
式中ρ代表流体密度,µ代表流体速度.

由动量守恒定律,Navier-Stokes(N-S)方程为[17]

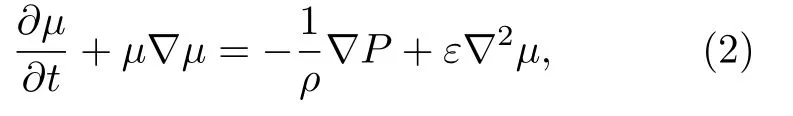
式中ε代表流体运动黏度,P代表流体压力.

由于超声空化过程中空化气泡状态变化涉及气-液两相流.所以采用气体体积分数函数αq来追踪流体中空化气泡的边界变化情况.用VOF 模型模拟气-液交界面[23],在VOF 模型中各部分流体不能相互穿插,体积分数的连续方程及约束条件分别由(3)式和(4)式表示:

其中,q代表流体的相,αq代表流体在网格中所占空间的比重.

2.2 有限元模型

理论分析大多是基于球形空化气泡的假设,但实际的空化气泡并不总是保持球形[24].为了让数值模拟的过程更接近实际情况,构建了图1 所示的三维仿真分析模型,图中的流体环境为底面半径为0.2 mm,高0.4 mm 的圆柱体区域,初始时刻存在两个半径R0=0.00309 mm 的球形空化气泡.

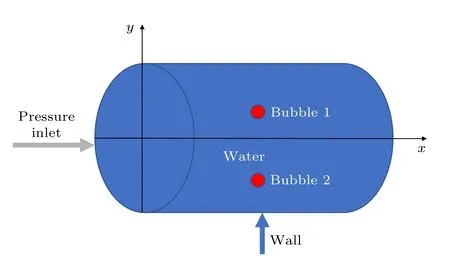
图1 计算模型Fig.1.Model for the calculation.

对Fluent 计算过程中的边界状态进行设置:1)左侧边界Pressure inlet 为声压入口边界.输入驱动声压函数P=Pasin(2πft) 用UDF 方式写入;2)边界壁面采用刚性壁面;3)空化气泡内部边界设为interior.Fluent 计算过程中的参数设置如表1 所示.

表1 Fluent 参数设置Table 1.Parameter setting of Fluent.

2.3 双泡耦合在一个声波周期内的超声空化演化过程

利用Fluent 求解计算了在超声波驱动下双泡耦合超声空化在一个声波周期内的演化过程.在整个求解过程中,将超声波频率设为f=25 kHz,驱动超声波声压幅值设定为Pa=1.29 atm (1 atm=1.013×105Pa),由于超声波驱动信号的周期T=40 µs,因此设置每一时间步长是0.01 µs,总步数为4000 步.图2 所示为双泡耦合超声空化在一个超声波周期内的演化过程.

从图2 可以看出,初始为理想球形的空化气泡在超声波开始输入后先缓慢扩张,其中图2(a)—(h)为空化气泡扩张阶段,约在t=18.80 µs 空化气泡扩张到最大半径;空化气泡在扩张到最大半径后开始收缩,约在t=22.55 µs 时溃灭.从数值模拟获得的空化气泡形态变化图可以看出,在超声波驱动下的空化气泡形状变化并不是规则的球形[25],而是沿声波激励方向逐渐往空化气泡的两端分裂,这也与文献[26]实验观测结论相符.由于能在声场中悬浮的空化泡都很小,一般很难直接观测到气泡的形状,许多研究人员对气泡周围液体环境中各物理量的变化进行研究来分析气泡的运动状况.2001 年,Wang 等[27]为了研究非球形声场下的气泡动力学行为,定义了描述气泡形变的参量,用来表征气泡偏离球形的程度,这一参量的取值与声场参数有关.其研究表明,声场的非球形对称性越明显,则气泡的非球形对称性越明显.

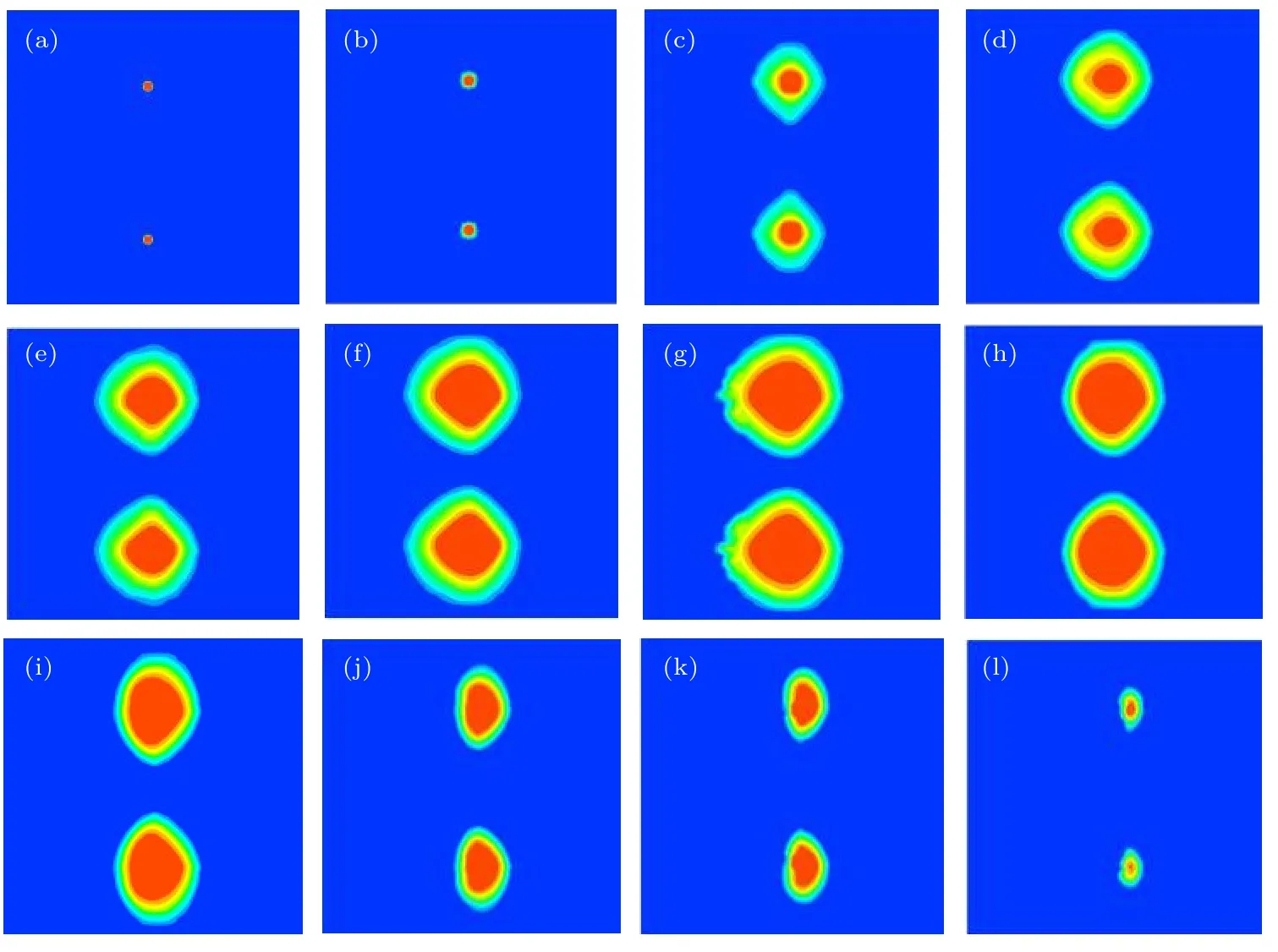
图2 不同时刻气泡的形态变化情况 (a) 0 µs;(b) 4 µs;(c) 8 µs;(d) 10 µs;(e) 12 µs;(f) 14 µs;(g) 16 µs;(h) 18.80 µs;(i) 20 µs;(j) 22 µs;(k) 22.2 µs;(l) 22.4 µsFig.2.The shape change of the bubble at different time: (a) 0 µs;(b) 4 µs;(c) 8 µs;(d) 10 µs;(e) 12 µs;(f) 14 µs;(g) 16 µs;(h) 18.80 µs;(i) 20 µs;(j) 22 µs;(k) 22.2 µs;(l) 22.4 µs.

在观察空化气泡的演化过程中发现,随着空化泡体积的增大,垂直声波激励方向上空化气泡两侧存在变形不对称的现象,在收缩阶段,这种现象更加明显,为了进一步研究这一现象,本文对超声空化过程中空化气泡周围声场变化进行了研究.

3 双空化泡之间的相互作用

3.1 监测点设置

在进行超声空化模拟过程中发现,空化气泡内和气泡周围物理场会发生变化,于是本文在气泡内和气泡外围设置了一系列监测点,如图3 所示,并对超声空化过程中这些位置压强变化进行了数值模拟.在图3 中,p10和p20分别表示两个空化气泡中心位置压强,分别表示声压激励方向上间距为10 µm 的8 个点的压强,分别表示垂直声压激励方向上间距为10 µm 的12 个点的压强.

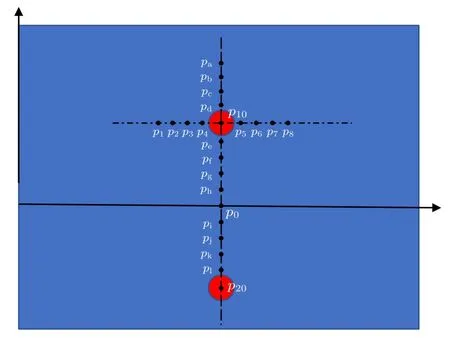
图3 监测点位置示意图Fig.3.Schematic diagram of the monitoring points.

3.2 双泡耦合超声空化过程中声场变化

本文对空化气泡内和气泡周围流场中不同位置压强变化进行了研究,数值模拟过程中各项参数设置与表1 相同,得到了各位置的压强变化如图4所示.

从图4 可以看出,在声波激励方向上,各监测点压强变化趋势都是从标准大气压开始减小,降至负压状态后经过一段时间开始增大至峰值,达到峰值之后在振荡中下降至标准大气压;垂直于声波激励方向上的监测点压强变化趋势与声波激励方向上相同;在垂直声波激励方向上,对比气泡1 两侧对称位置的压强变化发现,距离空化气泡中心距离相同的位置存在空化气泡一侧的压强数值低于无空化气泡一侧,即耦合气泡之间存在相互作用,使得双泡之间区域的压强减小[28].

图4 监测点压强变化 (a) 声波激励方向;(b) 垂直声波激励方向Fig.4.Pressure change of monitoring points: (a) Acoustic excitation direction;(b) vertical acoustic excitation direction.

为了研究耦合空化气泡之间的相互作用,对垂直声波激励方向各位置压强进一步研究,图5 所示是垂直声波激励方向上各位置压强随时间变化曲线.

通过观察图5 可以发现,当超声波开始激励时,各监测点的压强变化都是从标准大气压开始慢慢下降,这一阶段空化气泡处于缓慢扩张过程中,在这一过程中空化气泡两侧位置对称的监测点(pa与ph、pb与pg、pc与pf、pd与pe)的压强变化曲线基本重合,即在垂直声波激励方向上距离空化气泡中心相同距离处两侧压强变化基本一致;从t=20.04 µs 开始,空化气泡进入收缩阶段,各位置压强数值随着空化气泡半径减小而增大,与初始阶段曲线基本重合不同,ph先于pa开始变化,同样,pg先于pb、pf先于pc、pe先于pd,即在垂直声波激励方向上空化气泡两侧对称位置压强变化出现明显差异,存在耦合气泡的一侧压强先于无耦合气泡一侧开始变化.

图5 垂直声波激励方向监测点压强变化Fig.5.Pressure changes at monitoring points in the direction of vertical acoustic excitation.

为了对这一现象进行进一步研究,将同样驱动声场中只存在单气泡和耦合双气泡在收缩阶段压强变化曲线进行比对,如图6 所示.

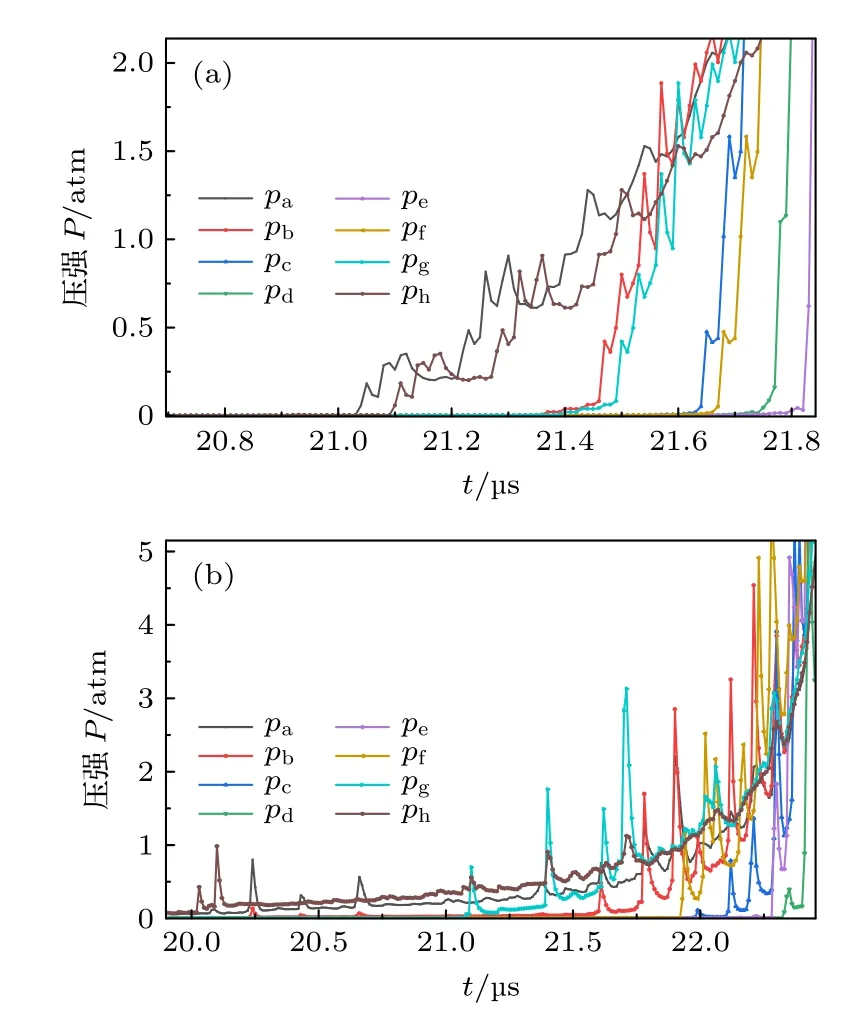
图6 塌缩阶段监测点压强变化 (a) 单气泡;(b) 耦合气泡Fig.6.Monitor pressure changes at the point during collapse: (a) Single bubble;(b) coupled bubble.

从图6 可以看出,在空化气泡收缩阶段,单气泡和耦合双气泡附近压强变化都是在振荡中增大,耦合双气泡附近的压强变化振荡幅度更大;单气泡和耦合双气泡两侧对称位置压强开始变化的时刻不同,将单气泡和耦合双气泡在垂直声波激励方向上两侧对称位置压强开始变化时间差进行比对,如表2 所示.

表2 空化泡两侧位置压强变化起始时刻差Table 2.Initial time difference between pressure changes on both sides of cavitation bubble.

从表2 可以看出,在垂直于声波激励方向上,空化气泡两侧对称位置压强变化时间差沿着气泡中心向外逐渐增大.以距离空化气泡中心40 µm处位置为例,单气泡在该位置压强开始增大的时刻约为21.17 µs,两侧对称位置开始增大的时间相差约为0.06 µs;双气泡耦合时,存在耦合气泡的一侧(两泡之间的位置)压强开始增大的时刻为20.02 µs,与另外一侧对称位置压强开始增大的时间相差约1.02 µs.对比单气泡可以发现,耦合双气泡彼此相互作用,相互作用力对空化泡的径向振动周期产生影响.相比于单气泡,耦合双气泡扩张阶段缩短,更早进入收缩阶段.采用Matlab 图像处理算法,对各个阶段空化泡的形态图像加以处理,对图像进行计算并转化为空化气泡截面面积,从而计算出各个时刻空化气泡的归一化半径Rmax/R0.表3 列出了相同超声波驱动下单气泡和双气泡耦合时空化气泡扩张阶段半径的最大值、溃灭时刻空化泡内部压强最大值及其出现的时刻.

表3 不同空化气泡最大半径和气泡内部最大压强(Pa=1.29 at m,f=25 kHz,R10=3.09 μm,R20=3.09 μm)Table 3.The maximum of radius and inside pressure of two kin ds of bubbles (Pa=1.29 atm,f=25 kHz,R10=3.09 μm,R20=3.09 μm).

从表3 可以看出: 在空化气泡扩张阶段,单气泡在t=19.20 µs 时扩张到最大,最大半径Rmax=30.75 µm,耦合双气泡在t=18.80 µs 时扩张到最大,最大半径Rmax=26.64 µm.相对于单气泡,耦合双气泡在扩张阶段的最大半径较小、扩张时间较短,由此表明耦合双气泡之间的相互作用抑制了气泡的扩张.空化气泡在收缩过程中,泡内压强随着气泡收缩不断增大,当空化气泡收缩至最小半径时气泡溃灭,发生剧烈的空化现象,此时气泡中心位置压强达到最大值.由表3 可知,单气泡在t=22.01 µs 时气泡中心位置压强达到最大值Pmax=77.21 MPa,耦合双气泡在t=22.55 µs时气泡中心位置压强达到最大值Pmax=81.81 MPa,相比于单气泡,双泡耦合时空化气泡收缩阶段时间延长,空化气泡溃灭时气泡内部压强增大.在一个驱动超声波周期内,单泡的径向振动周期T=22.01 µs,耦合双气泡的径向振动周期T=22.55 µs,耦合双气泡之间的相互作用改变了气泡的振动周期;耦合双气泡溃灭时气泡内部的压强较单气泡有所增大,即耦合双气泡的相互作用提高了声空化气泡的能量转换效率,该结论也与文献[28]中所叙述一致.

4 结论

本文使用Fluent 软件构建了双气泡耦合超声空化的三维有限元仿真模型,并对超声波驱动下水中双气泡耦合的空化动力学过程进行数值模拟.在此基础上,研究了双气泡耦合声空化动力学过程与空化气泡内和气泡周围压强变化的关系,并与相同超声波驱动下单气泡空化过程做了对比分析.

1)在双气泡耦合超声空化过程中,耦合双气泡内和泡外附近流场压强变化趋势是从标准大气压先减小至负压状态,一段时间后从负压状态开始增大达到峰值,最后在振荡中减小至标准大气压;空化气泡内外压强变化与气泡体积变化成反比.

2)耦合双气泡之间存在相互作用力,空化气泡之间的相互作用对空化气泡的扩张有抑制作用,在耦合双气泡扩张过程中,相比于单泡,耦合双气泡的最大半径减小、膨胀时间缩短;对空化气泡的收缩有加剧作用,在气泡收缩阶段,相比于单泡,耦合气泡收缩开始时间提前、持续时间延长;空化气泡的径向振动周期发生了变化.

3)耦合双气泡相互作用于彼此,增加了空化气泡的能量转换能力.在空化气泡溃灭时,耦合气泡内压强大于单气泡内部.空化气泡耦合使得空化现象更为剧烈.

本文研究结果对研究超声空化泡群动力学行为具有一定的参考价值,后续还将继续进行相关研究.