基于无人机集群的近场线性稀疏阵列波束形成研究

张逸楠 王广学 彭世蕤 冷 毅

(空军预警学院信息对抗系 武汉 430019)

1 引言

波束形成是通过调整阵列中各个阵元发射或接收信号的振幅和相位，使得阵列可以从特定的方向观测信号，同时衰减其他方向信号响应的技术[1,2]，在众多领域得到了广泛应用，如声呐、超声成像、电子对抗、通信系统等[3-8]。随着战场从有人化向无人化发展，无人机集群的应用成为研究的热点。据美军事与航空电子网2019年5月21日的报道，美国空军实验室(Air Force Research Laboratory)与智能自动化公司(Intelligent Automation Inc.)签订了用于无人机集群的分布式相控阵天线系统合同，通过集群间的协同将各无人机配备的天线阵元组合成分布式波束形成系统，以实现定向高增益信号传输，标志着美军正规划利用波束形成技术提升无人机集群在激烈对抗环境下的作战能力；此外，文献[9]公开了一种基于无人机群的3维组阵天线，通过机群的空间组合形成天线波束。可以预见，在通信、电子侦察、干扰等领域，无人机集群编队协同组成天线阵列，运用波束形成技术合成定向高增益波束是发挥集群作战效能的一个重要研究方向。

当前，关于阵列波束形成的研究成果有很多，如文献[2,10]针对宽带波束形成问题，比较分析了时域波束形成方法和频域波束形成方法的性能特点；文献[11]提出一种基于稀疏MIMO阵列和空间滤波器组(SFB)的高效波束形成方法；文献[12]提出了基于时频分析的盲波束形成算法，通过对信号的傅里叶变换，在频域估计信号参数，然后进行波束形成；文献[13]以最大输出信干比为准则，构造优化模型同时对天线子阵结构和每个子阵的波束形成矢量进行优化设计；文献[14]提出了一种基于机器学习的随机方差梯度下降自适应波束形成算法，提高了复杂环境背景下短快拍自适应波束形成的稳定度。上述研究均以电磁波的远场平面波辐射模型为基础，然而无人机集群构成的天线阵列规模可达数千米，导致近场范围大幅扩大，且由于受无人机尺寸和飞行安全的限制，无人机的编队间隔通常远大于波长，因此无人机集群构成的天线阵列常呈现近场、稀疏特性，远场波束形成无法适配。

与远场阵列波束相比，近场稀疏阵列在波束形成方法、波束增益变化特性、波束栅瓣分布特性等方面均存在差异，相关领域的研究成果还存在欠缺，给无人机集群的波束形成、波束扫描策略的设计与优化、波束栅瓣的抑制或利用带来了困难。为此，本文以经典的均匀线性阵列结构为基础，针对无人机集群阵列的近场稀疏分布特性，首先构建了与之对应的阵列信号模型，并通过运用泰勒展开式对信号模型中各阵元信号的相位差函数进行近似分析，得到了在空间域进行线性调频脉冲压缩处理的近场波束形成简化实现方法。而后，在空间-频率2维域内对近场波束形成特性进行了分析，从空间位置改变导致信号频率偏移和带宽失配的角度，分析得到了近场波束主瓣的方位向增益变化特性和距离向增益变化特性；从空间欠采样导致信号频谱折叠的角度，分析提出了近场波束栅瓣分布的解析表达式。最后，通过仿真证明了分析结论的有效性，为利用近场波束形成技术提高无人机集群的通信、电子侦察、干扰能力提供了理论支撑。

2 近场阵列信号模型与波束形成简化实现方法

2.1 近场阵列信号模型

在近场条件下，电磁波为平面波的假设不成立，需要采用球面波进行描述。如图1所示，设由N架无人机编队构成的N元近场稀疏天线阵列沿x轴等间隔线性分布，阵元间距大于半波长，阵列总

图1 近场线性稀疏阵列模型

由式(4)、式(5)可以看出，近场条件下不同阵元之间的信号相位差不仅与角度θ相关，而且与距离R相关。以此为基础，为使不同阵元的信号能够同相相加，经典的近场波束形成方法可表示为[15]

2.2 近场波束形成近似简化实现方法

对比式(11)、式(12)可知，h(x)可 视为st(x)的脉冲压缩滤波函数。以此为基础，式(10)所述近场波束形成简化实现方法相当于在空间-频率2维域内采用滤波器h(x)对 信号s(x)进行脉冲压缩处理，当感兴趣目标位于主瓣峰值点时，h(x)与s(x)恰好相匹配，从而可获得最大的脉冲压缩处理增益。

3 基于空间-频率2维域的近场波束形成特性分析

由式(10)可以看出，近场波束F(R,θ)是关于距离R和角度θ的二元函数，即近场波束形成是将主瓣聚焦在一个点，而远场波束形成与距离R无关，是关于角度θ的函数，两者的波束增益变化特性存在明显差异，因此有必要对近场波束形成的增益变化特性进行分析，从而为后续的系统设计提供理论支撑。

3.1 距离向波束增益变化特性分析

3.2 方位向波束增益变化特性

当方位向上的角度变化，距离向上的斜距不变，信号同时存在中心频率偏移和带宽失配。此时从中心频率偏移和带宽失配的角度，可以分析近场波束在方位向上的特性。

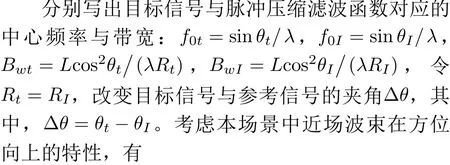
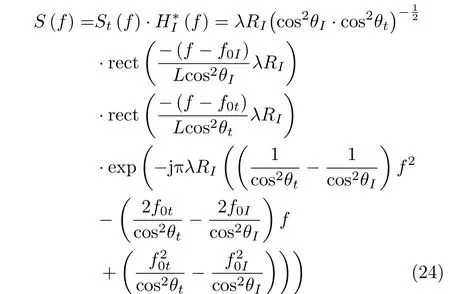
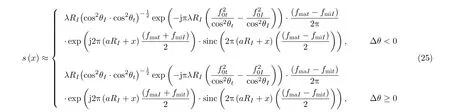
3.3 近场波束栅瓣分布特性

文献[16-19]对栅瓣的抑制方法作出了讨论，而文献[20]利用了发射栅瓣进行成像。无论是抑制栅瓣抑或利用栅瓣，已知栅瓣的分布是前提条件。文献[21]就二元稀疏阵的交叉波束合成进行初步分析，提出利用某方向的波失投影求解另一方向的栅瓣分布，但忽略了电磁波在各个方向都存在波失的特性，该方法仅适用于两方向夹角较小时的近似，具有局限性。实际上，对于二元稀疏阵的交叉波束合成，如图2所示，可将两阵元看作双曲线的焦点，通过双曲线簇的性质得出栅瓣分布。

图2所示双曲线簇方程

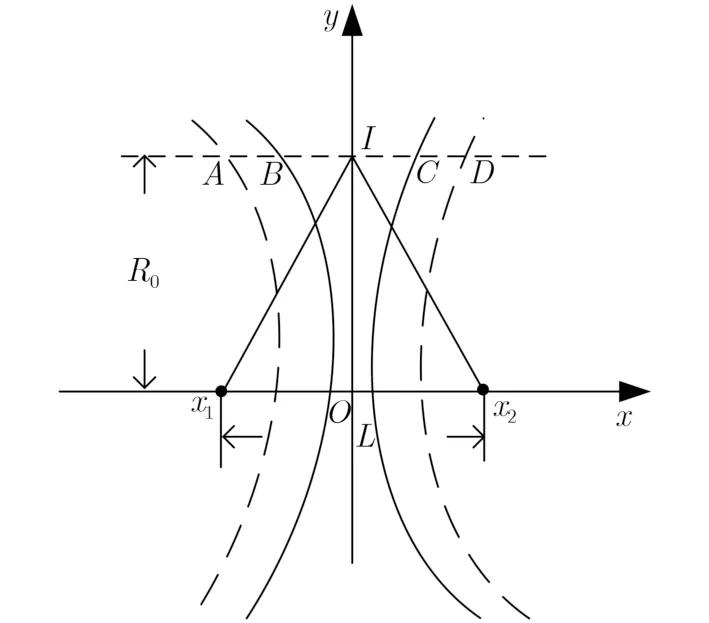
图2 两阵元的双曲线簇模型

该法适用于二元稀疏阵在任意目标距离处的栅瓣分布推导。

目前较少文献讨论多元稀疏阵的栅瓣分布情况，根据以上分析，各阵元信号在空间-频率2维域内可近似为线性调频信号，阵列稀疏相当于对信号进行欠采样，信号变换到频域时会以采样频率为周期进行频谱延拓，即信号频谱产生折叠，当折叠后的信号频谱与滤波函数频谱相匹配时，会出现栅瓣。则利用奈奎斯特采样定理求解多元稀疏阵的栅瓣分布问题，有

若按照远场均匀线阵栅瓣分布推导公式[22]，均匀直线阵阵因子的最大值出现在ψmy=kdsinθmy=m·2π,m=0,±1,±2,...处 ，其中，ψmy表示两相邻单元辐射场的相位差，d=L/(N-1)为阵元均匀分布的间距，θmy为阵列第m个最大值方向与阵列法向的夹角。可解得

此时，θmy=θm，说明当θI=0时，近远场同序号栅瓣在同一个方位向上，但远场不考虑距离向的影响，而近场需考虑栅瓣在波束距离向上的特性。

4 仿真分析

4.1 近场波束形成简化实现方法

设信号频率f=300 MHz ，波束中心指向I点θI=0°或θI=2°。阵 元 数N=26，阵 列 孔 径L=500λ， 考察距离阵列Rt=[30 km,50 km]处主瓣波束形成，即θI=0°时，θt=[-2°,2°]对应目标场强 值，θI=2°时，θt=[0°,4°]对 应 目 标 场 强 值。利用经典波束形成方法与近似波束形成方法形成波束如图3、图4所示，其中，图3(a)、图3(b)与图4(a)、图4(b)分别为θI=0°与θI=2°时的波束3维图，由于仿真选取的阵元间距大于λ/2，波束均存在栅瓣，图3(c)、图3(d)与图4(c)、图4(d)分别为θI=0°与θI=2°时的波束主瓣功率变化情况。

由图3、图4，不论波束扫描与否，经典方法形成的波束与近似形成的波束一致，验证了脉冲压缩处理适用于本文所提近场波束形成方法以及本文所提近场波束近似形成方法的有效性；经补偿后波束主瓣峰值功率皆可达28 dB，接近26个阵元可达功率峰值28.30 dB。

图3 θ I =0°时经典与近似波束形成比较

图4 θ I =2°时经典与近似波束形成比较

4.2 近场波束主瓣分布特性算法验证

设θI=0°，无人机群侦察时波束中心指向RI=80 km ，ΔR=[-20 km,20 km]；无人机群干扰时波束中心指向RI=30 km， ΔR=[-10 km,10 km]，阵列孔径L=2000λ，其余仿真条件不变。分别得到距离向上的实际波束图与式(22)、式(23)得到的波束图做比较，如图5所示。

由图5(a)，在RI较 大时，ΔR变化较小时以式(22)估计实际波束更贴近，随着ΔR变化增大，实际波束变化趋势与式(23)一致；由图5(b)，在RI较小时，ΔR变化较小时实际波束变化趋势也符合式(23)，与对距离向波束特性理论分析一致。

图5 距离向波束图

设Rt=RI，θI=0，θt=[-1°,1°]， Δθ=[-1°,1°]， 阵列孔径L=500λ，其余仿真条件不变。分别得到方位向上的实际波束图与对主瓣宽度范围内的近似波束图做比较，如图6所示。

图6 方位向波束图

由图6可见，近似波束主瓣与实际波束主瓣一致，近似波束副瓣整体变化趋势与实际波束副瓣一致但近似副瓣变化更加剧烈，原因在于，当 Δθ增大到离开主瓣区域，近似式将与实际式有较大误差，因此不能贴合实际波束副瓣变化，仿真结果验证了方位向波束特性理论分析的有效性。

4.3 近场波束栅瓣分布特性算法验证

设波束中心指向I(40 km,0°)，考察斜距范围Rt=[30 km,50 km]，θt=[-8°,8°]的目标，根据式(6)，其功率值随角度与距离变化如图7所示。

将阵列实际形成的波束，即图7所示波束，分别投影到θ-R,θ-P,R-P平面，并用栅瓣分布推导公式计算该波束指向对应的栅瓣，如图8所示。

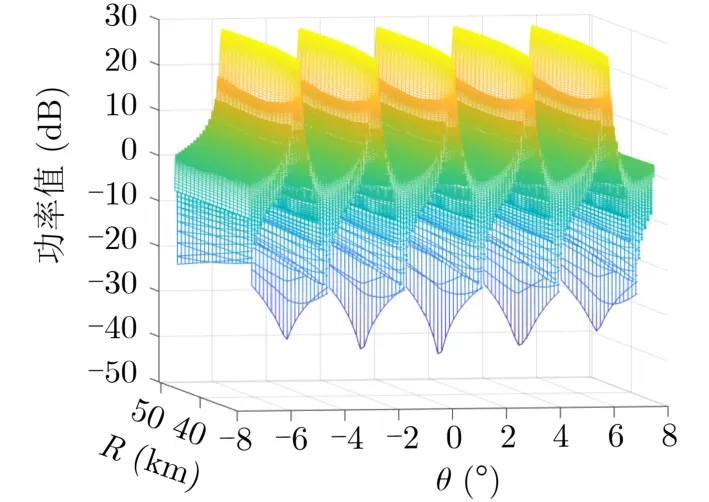
图7 曲面范围内目标波束图

图8(a)-图8(c)中，红点与红线为由栅瓣分布式(31)计算所得。由图8(a)可见，随着θm变化，Rm也有一定的变化；在栅瓣出现的方位上画出随距离变化的功率图如图8(d)所示，不同序号的栅瓣峰值在距离向上是变化的，|m|相等的一对栅瓣的功率在距离向上的变化规律一致。图8显示了栅瓣分布公式(31)所求栅瓣与波束栅瓣分布一致，验证了式(31)栅瓣分布求解方法的有效性。

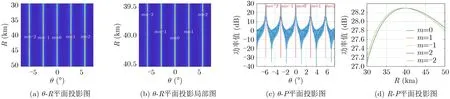
图8 波束投影及栅瓣分布计算

波束扫描时，设波束中心指向I(40 km,2°)，其余仿真条件不变，得图9。

用栅瓣分布推导公式计算该波束指向对应的栅瓣，如图10所示。

由图9、图10，应用式(30)求得的栅瓣分布与波束实际栅瓣分布一致，不同序号的栅瓣峰值在距离向上是变化的，扫描情况下|m|相等的一对栅瓣在距离向上的特性也不同。图10显示了栅瓣分布式 (30)所求栅瓣与波束栅瓣分布一致，验证了式(30)栅瓣分布求解方法的有效性。

图9 波束扫描曲面范围波束图

图10 波束扫描投影及栅瓣分布计算

5 结束语

为解决无人机集群的近场波束形成、波束扫描策略的设计与优化、波束栅瓣的抑制或利用等问题，本文首先构建了与无人机集群阵列的近场稀疏对应的阵列信号模型，并通过泰勒展开式对信号模型中各阵元信号的相位差函数进行近似分析，得到了近场波束形成简化实现方法。而后，在空间-频率2维域内对近场波束形成特性进行了分析，基于奈奎斯特采样定理推导出近场波束栅瓣分布的解析表达式；从空间位置改变导致近场信号频率偏移和带宽失配的角度，分析得到了近场波束分别在方位向和距离向的增益变化特性。最后通过仿真证明了分析结论的有效性，为利用近场波束形成技术提高无人机集群的通信、侦察、干扰能力提供了理论支撑。无人机群作为阵列时，作为阵元的单架无人机的抖动与定位会带来位置误差，影响波束形成，随着信号波长变小，波束形成对位置误差将变得更敏感，如何进行误差的补偿，是后续需继续研究的问题。