基于宽频振荡稳定约束的风电接入容量分析

吴琛，刘威，张丹，谢小荣，黄伟，郑超

(1.云南电网有限责任公司规划建设研究中心，昆明市 650011； 2.清华大学电机工程与应用电子技术系，北京市 100084；3.云南电力调度控制中心，昆明市 650011)

0 引 言

风电、光伏等清洁能源的开发和利用对于“双碳”目标的达成具有重大意义[1-2]。近十年来，由于风电技术的逐渐成熟，其发电成本下降，风电总装机容量大幅度提高[3-4]。其中，直驱或半直驱风电机组(wind turbines generator，WTG)由于发电效率高、可靠性高的特点，在新规划建设的风电场中被广泛采用。随着对风电消纳能力要求的提高，直驱和半直驱风电机组存在大型化的发展趋势，近年新兴机型的单机容量大多为4 MW及以上，经过背靠背运行的大容量全变流器接入电网[5-6]。不过，此类经全变流器的风电机组可能因控制器与交直流电网间的相互作用引发宽频振荡[7-8]。这些宽频振荡问题严重影响了电力系统的安全稳定运行，限制了风能的消纳能力。

为了应对风电并网引发的宽频振荡问题，目前主要从两个方面开展研究。其一是在风电场规划设计阶段进行充分的论证，提前预测到风电场是否存在宽频振荡风险以及发生宽频振荡的条件，从而在建设和运行时规避可能引发宽频振荡的运行方式[9-10]。其二是采用具有阻尼控制能力的风电机组和装置，消除宽频振荡风险或对发生的宽频振荡进行抑制[11-13]。两个方面相结合，才能较好满足电力系统安全稳定运行的要求。在论证风电场的宽频振荡风险时，风电场的接入容量和风电场接入电网的电气距离(通常使用阻抗表示)是需要考虑的重要因素，通常可以采用时域仿真法进行分析[14-16]。不过，时域仿真法每次只能分析单一运行方式，在运行条件变化范围较广时，效率较低。且时域仿真法仅能提供定性结果，无法分析某种运行方式下宽频振荡的稳定裕度。目前，阻抗模型法已被广泛用于风电宽频振荡的分析[17-18]。该方法要求分别建立风电场和电网的阻抗模型，通过阻抗模型频率特性评估宽频振荡的风险，目前常用于分析某些给定运行方式下风电并网后的振荡特性。然而，在实际工程中，通常更关注风电场接入电网后是否存在以及何种条件下才会引发振荡、电网所能承载的最大风电容量等，这对风电场近期的建设和运行、乃至远期的扩建等具有较高参考价值[19-20]。

为此，文中围绕风电并网系统的宽频振荡问题对风电场接入容量与电网阻抗的关系进行分析。首先，给出风电场并网系统的典型结构，建立风电机组的全工况阻抗模型。然后，分析风电机组运行条件变化对宽频振荡稳定性的影响，得到宽频振荡约束下的风电场接入容量与电网阻抗的关系。最后，通过时域仿真对全工况阻抗模型分析得到的结果进行验证，说明其准确性。根据分析结果，可以确定在相应的电网条件下，风电场在不引发宽频振荡前提下的最大接入容量，为风电场的规划设计提供指导，对从源头消除宽频振荡风险、保障电力系统稳定具有重要的积极意义。

1 风电并网系统及其阻抗模型

1.1 风电并网系统

图1为典型风电并网系统的简化结构图。假设风电场内风电机组的数量为N，风电场内各风电机组汇集后通过交流输电线路直接接入交流电网，接入线路的等效电阻和电感分别为RL和LL，交流电网电压为UG。

图1 风电并网系统Fig.1 Wind power system

在实际风电场中，由于地理位置不同，不同的风电机组运行条件、及所接馈线长度等均存在差异，给整个风电场并网的稳定性分析带来了困难[21-22]。由于关注的是宽频振荡稳定约束下的风电接入容量分析，一般需要考虑运行条件最为恶劣的情况[23-24]。通常，场站内可能存在多种型号且特性不同的风电机组，若在同一条件下，某台风电机组并网后负阻尼作用最显著，即最易引发宽频振荡，则可假设场站内各风电机组型号一致，均为该负阻尼作用最显著的风电机组，以使整个系统的负阻尼最大化、运行条件最恶劣，同时这一假设也可提高分析效率[25-26]。此前，在次/超同步等振荡相关研究中，也常将整个风电场视为多台完全相同的风电机组并联，其精度一般满足要求[27-29]。

场站内各风电机组型号一致，采用图2的等值模型表示，其中各参数(含PI控制器参数)的符号及含义详见表1。在风电机组容量较大时，直流侧选用的容值通常也较大，此时直流对机侧动态的隔离作用显著，风电机组的机械至机侧变流器(machine-side converter，MSC)部分对并网动态影响较弱，风电机组的宽频振荡特性主要与网侧变流器(grid-side converter，GSC)相关[25, 30-31]。考虑到这一因素，可将机械至MSC部分等效为直流电源，其注入直流侧的功率Pin大小取决于风速和机侧功率控制参考值[32-33]。GSC采用典型的dq解耦控制方法，其中d轴采用直流电压外环控制，用以维持直流电压的恒定；q轴采用无功功率外环控制，用以控制风电机组输出的无功功率，调节功率因数。

表1 风电机组(含控制)及变压器参数Table 1 Parameters of WTG and transformer

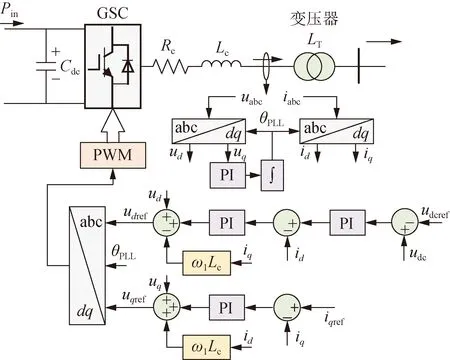
图2 风电机组及其变流器控制Fig.2 Wind turbine generator and its converter control

1.2 全工况阻抗建模

通过阻抗建模方法可以建立风电机组的阻抗模型。由于直驱风电机组在中低频段具有明显的频率耦合效应，为了准确，文中将采用频率耦合阻抗模型[34]，即：

(1)

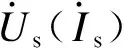
风电机组的阻抗模型是建立在工作点附近的小信号模型，因此，当风电机组的运行点发生变化时，阻抗模型的大小也将发生变化。例如，当有功和无功功率变化时，风电机组的阻抗模型也随之改变。文献[35]中提出了一种全工况阻抗建模方法，按照文中所提方法，可以将阻抗模型表示为：

(2)

式中：矩阵Y={Yij(s)}2×2为频率耦合导纳模型；U1、Id和Iq分别为工频电压幅值、电流有功和无功分量；x为三者构成的工况向量；T表示取转置；Gij和G0为四维模型参数方阵，可表示为[35]：

(3)

式中：ak、bk、ck和α均为模型参数(向量)，仅由控制结构和参数决定，与运行工况无关。

按照式(2)—(3)，推导图2所示风电机组的全工况阻抗模型的模型参数(向量)ak、bk、ck和α，结果如表2所示。

表2 模型参数Table 2 Model parameters

表2中，Ki(s),i= 1, 2, …, 8分别为：

(4)

式中：Gd(s)、Gq(s)和Gdc(s)为风电机组控制参数构成的传递函数，即：

(5)

上述全工况阻抗模型将运行工况相关的参数，如风电机组并网点电压(U1)、输出电流(Id和Iq)等，与风电机组运行过程中基本不变的结构和控制参数等进行了分离，便于直接分析风电机组并网点电压和输出功率变化等对宽频振荡稳定性的影响。为了采用上述模型进行分析，首先应通过网络计算得到风电机组并网点的工频电压和电流。若认为风电机组并网点的电压相位为基准点，则需要根据单台风电机组的输出功率计算并网点电压的幅值U1、电流有功分量Id和无功分量Iq。根据电路关系，可以列入如下方程：

(6)

式中：ω1=2πf1表示工频；UG为交流电网电压；I1、P和Q为风电机组输出电流、有功功率和无功功率。

对于特性基本不随运行工况变化的变压器和输电线路，二者的频率耦合阻抗模型ZT(s)和ZL(s)可以直接写为：

(7)

(8)

2 宽频振荡稳定性分析

2.1 风电机组并网宽频振荡稳定性分析

2.1.1 基于全工况阻抗模型的宽频振荡分析

不妨假设电网参数不变，将线路阻抗和变流器阻抗均换算至低压侧并求和得到电网侧的等效阻抗Rg和Lg，进而分析单台风电机组宽频振荡特性。

若保持Rg=0.01 Ω，Lg=0.52 mH，其他参数取值如表3所示。

表3 各变量取值Table 3 Values of all parameters

通过计算，此时风电机组接入点的短路比固定为1.38。通常，风电机组的输出功率因数应不低于0.95(超前或滞后)，且其端口正常工作电压应为0.90～1.10 pu。在该运行范围下，分析风电机组输出有功和无功功率变化时，并网系统的宽频振荡稳定性，主要步骤为：

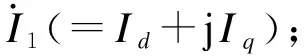
2)将所求并网点电压U1和输出电流I1代入全工况阻抗模型，即式(2)，得到对应运行工作点下风电机组的阻抗模型ZWTG(s)；

3)结合电网侧变压器和输电线路阻抗模型，即式(7)和(8)，计算得到聚合阻抗模型ZΣ(s)，即：

(9)

4)计算聚合阻抗行列式零点|ZΣ(s)|=0，若所有零点实部小于0，则系统不发生振荡，实部为0说明在对应工作点下系统临界稳定。

分析结果总结如图3所示，其中阴影部分指系统可以在这些工作点下保持稳定运行，而稳定性边界则是由聚合阻抗行列式零点实部恰好为0的运行工作点构成的。图3表明风电机组接入点电网短路比为1.38时，在满足功率因数约束和端口电压约束的情况下，随着有功功率的增大，该单机并网系统可能出现不稳定的振荡现象，即对应稳定性边界右侧的工作点。从图3可以发现风电机组存在三个关键的有功功率点，分别记作P1、P2、P3。当风电机组输出的有功功率PP2时，在任意满足功率因数和端口电压约束时，系统始终不稳定。当PP3时，风电机组在额定运行电压下不稳定。图3中，P1、P2和P3分别为0.645 pu、0.845 pu和0.782 pu。

图3 风电机组宽频振荡稳定性分析Fig.3 Wide-band oscillatory stability analysis of wind turbine generator

考虑端口电压保持为额定电压的运行工况，可以绘制系统聚合阻抗行列式零点随功率变化的曲线，如图4所示。图4表明，在短路比为1.38时，若输出的有功功率从0逐渐增大至1.00 pu，则聚合阻抗行列式零点将逐渐右移，在增大至0.78 pu以上时，零点位于复平面的右半平面，即系统不稳定，此时振荡频率为28.5～30.6 Hz(对应超同步71.5～69.4 Hz)变化。

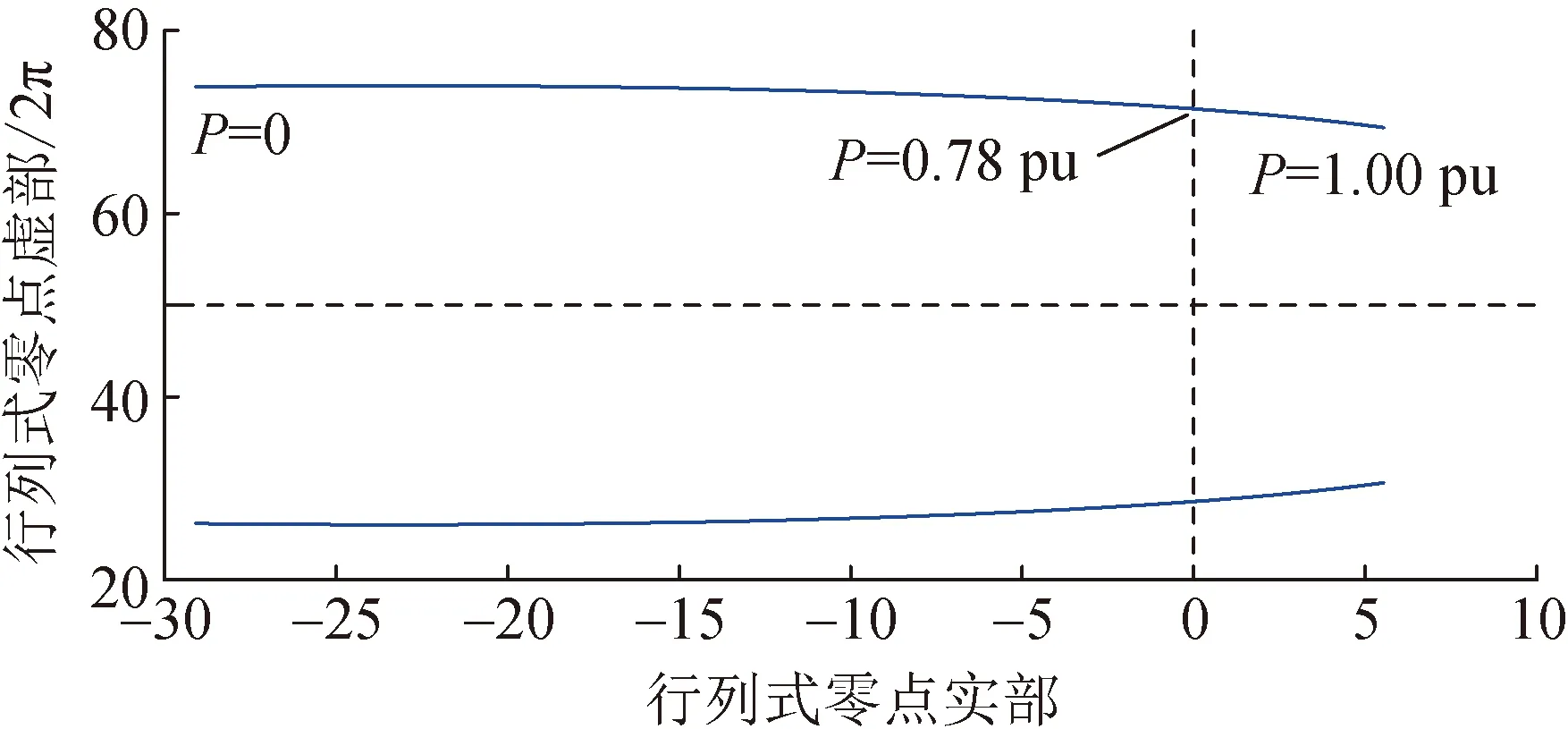
图4 聚合阻抗行列式零点随有功功率变化Fig.4 Variation of zero point of aggregated impedance determinant with active power

2.1.2 电网短路比对振荡稳定性的影响

接入点的短路比增大，可以有效增大风电机组的稳定运行范围。为说明这一结论，此处分析短路比变化时的关键有功功率参数P1、P2和P3，结果如图5所示。可以看出，若使风电机组输出功率为1.0 pu时系统能够不发生振荡，则风电机组接入点电网的短路比至少应为1.61，而且此时只有在输出无功功率较大时系统才能保持稳定；若使系统能够在风电机组输出任意有功和无功功率下始终保持稳定，则接入点短路比应高于2.13；若要求风电机组在额定电压和额定功率下保持稳定运行，则接入点短路比应大于1.75。

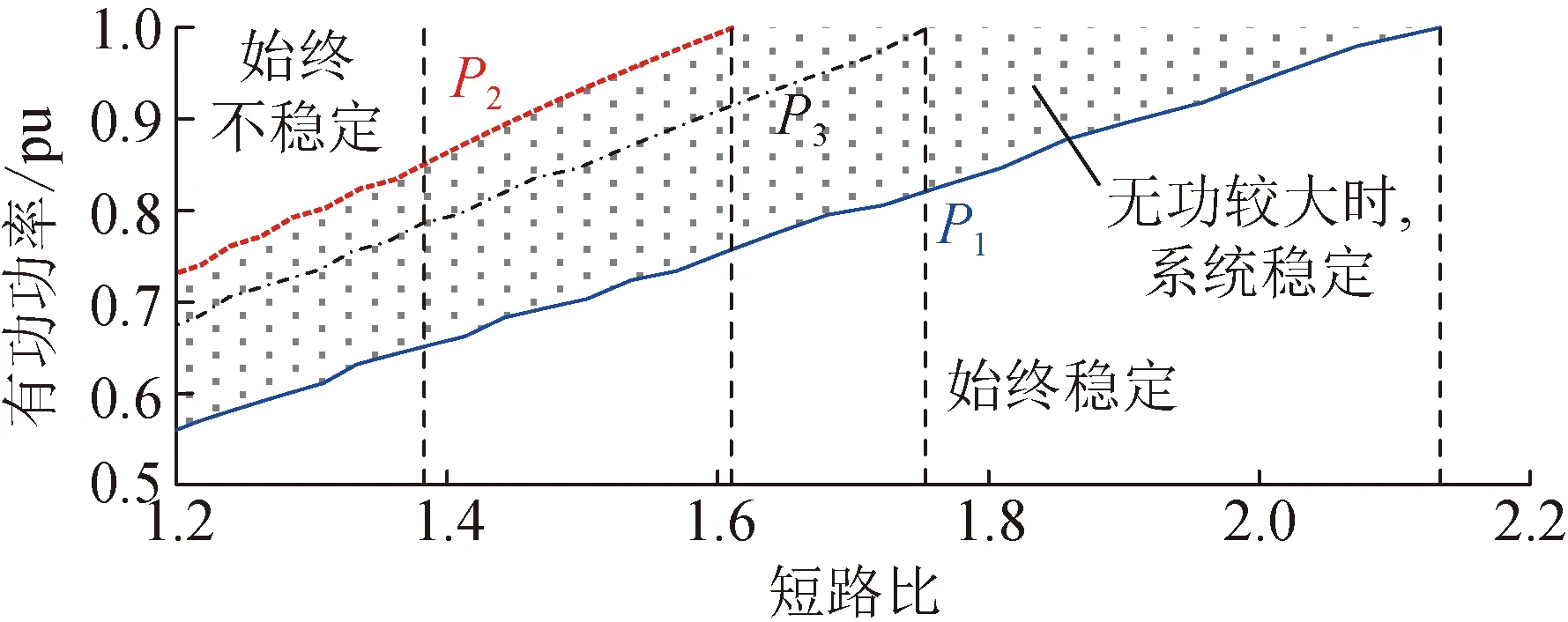
图5 临界振荡稳定时有功功率随短路比变化Fig.5 Variation of active power with short-circuit-ratio at critical oscillatory stability

2.2 考虑宽频振荡约束的接入容量分析

考虑风电场中众多风电机组同时并网，风电场接入点等效的电网短路比可以估算为：

(10)

式中：SWTG为单台风电机组的容量；ZL为线路阻抗。

显然，随着风电机组并网数量N的增多(即风电场容量增大)或线路阻抗ZL的增大，接入点等效的短路比减小，稳定性变差，振荡风险增大。

假设某一条件下，风电场中所有风电机组的参数和运行条件完全一致，且引发振荡的临界短路比为Kc，则在线路阻抗ZL不变的情况下，可以根据式(10)得到不发生振荡时风电机组的最大并网数量，即

(11)

根据图5所示结果，对于所分析的风电机组，若要求每台风电机组在任意输出功率下系统均保持稳定，此时应满足KSCR-WF≥ 2.13，此时对应的并网风电机组数量最少，容量最小。结合式(11)可计算此时的风电机组数量Nmin和风电场总容量Smin，即：

(12)

若仅要求每台风电机组在功率因数为0.95(输出无功功率最大，最不易发生振荡)、最大输出功率下能够保持稳定运行，短路比只需满足KSCR-WF≥ 1.61，此时对应的并网风电机组数量最多，容量最大；此时并网风电机组数量Nmax和风电场总容量Smax为：

(13)

若要求每台风电机组在额定电压和额定功率下，能够保持稳定运行、不发生振荡，则机组接入数量N和风电接入容量S约为：

(14)

通过全工况阻抗模型方法分析额定运行工况下风电机组数量N和线路电感LL变化时系统的宽频振荡稳定性，结果如图6所示。当线路电感增大时，在不发生宽频振荡的前提下风电场可容纳风电机组的最大数量逐渐减小，式(14)表明二者呈反比关系。根据这一结论可以在规划设计阶段对风电场并网后的宽频振荡稳定性进行校验。

图6 不同风电机组数量与线路电感下宽频振荡稳定性Fig.6 Wide-band oscillatory stability under different number of wind turbine generators and line inductance

3 仿真验证

3.1 单台风电机组仿真验证

在PSCAD/EMTDC中建立图1和图2所示的风电并网系统，通过单台风电机组电流倍乘模拟多台风电机组同时并网。

假设风电机组的数量N=1，线路参数RL=13.6 Ω，LL=0.625 H，换算至低压侧，与变压器漏感求和后得到的电网参数约为Rg=0.01 Ω，Lg=0.52 mH。在t=0 s时，风电机组输出有功功率为0.75 pu，输出无功功率为0.20 pu，此时系统稳定；而t=1 s时，无功功率不变，有功功率增大至0.80 pu，这时系统开始出现振荡，并且逐渐发散，如图7所示，这与图3所示的振荡稳定性分析结果一致。振荡发散阶段的频域分析如图8所示。图8表明，此时风电机组电流振荡频率约为29 Hz和71 Hz，功率中振荡频率约为21 Hz，这与图4所示的分析结果一致。

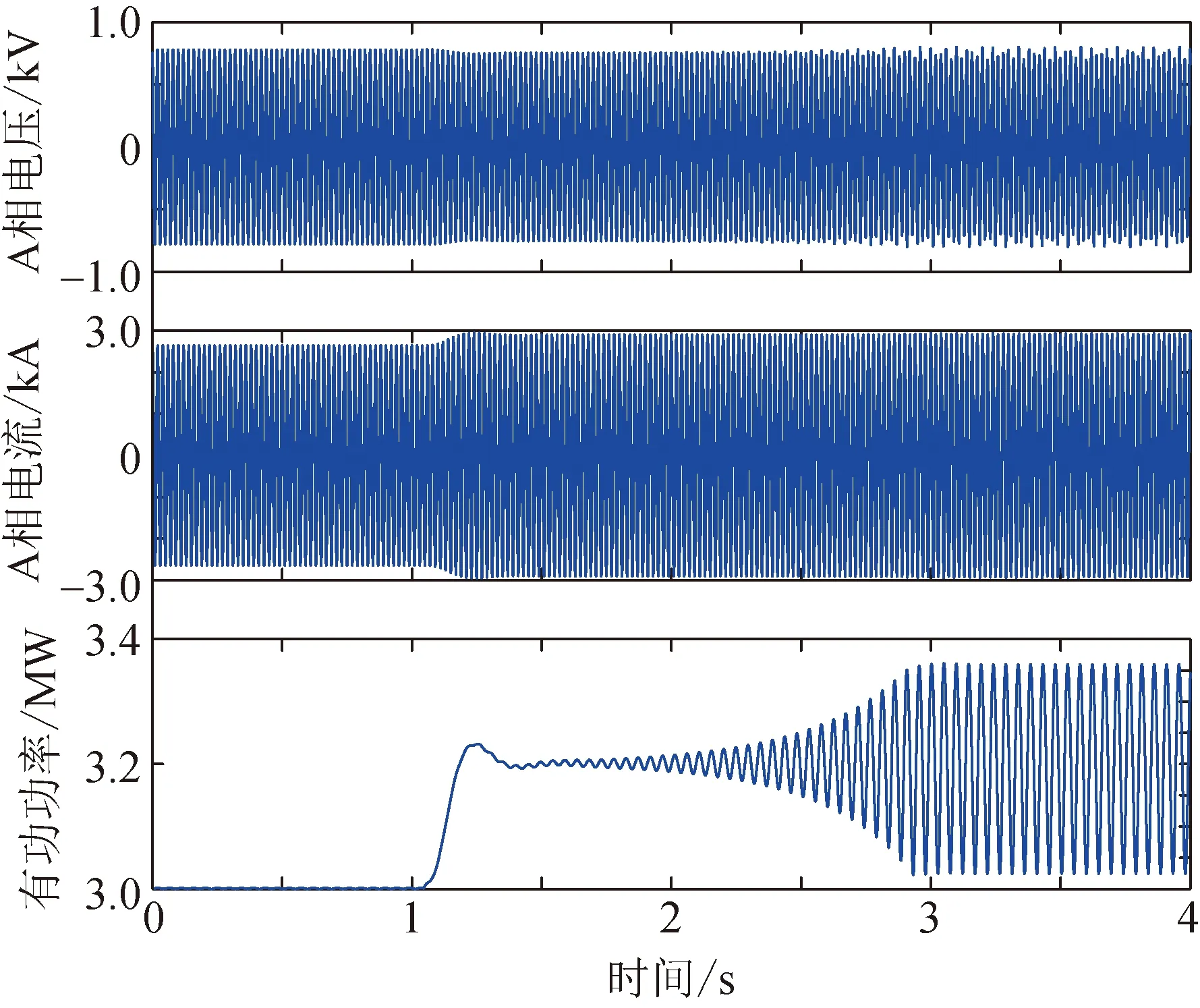
图7 功率变化时风电机组电压、电流和有功功率波形Fig.7 Voltage, current and active power of the wind turbine generator with different active power

图8 P=0.80 pu时风电机组电流和有功功率波形频域分析Fig.8 Spectrum of current and active power of the wind turbine generator when P=0.80 pu

3.2 多台风电机组仿真验证

假设线路参数LL=5 mH，RL=0.157 Ω，结合图6可知，在该线路参数下，若使风电机组在额定输出功率和额定电压条件时可保持稳定运行，则最大并网风电机组的数量约为110台(容量为440 MW)。为验证此结果，设置仿真条件为：t=0 s时，并网风电机组数量N=105，t=1 s后，N从105增至115。仿真中，单台风电机组电压、电流和输出有功功率变化如图9所示。

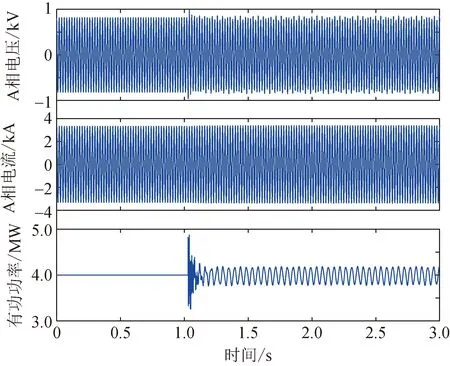
图9 并网机组数量变化时风电机组电压、电流和有功功率波形Fig.9 Voltage, current and active power of the wind turbine generator with different N

可以看出，并网的风电机组数量为105台(容量为420 MW)时，系统未发生振荡，而数量增至115台(容量增至460 MW)时，系统出现振荡，电流振荡频率约为28.2 Hz和71.8 Hz，功率中振荡频率约为21.8 Hz(见图10)，说明了图6所示结果的准确性。

图10 N=115时风电机组电流和有功功率波形频域分析Fig.10 Spectrum of current and active power of the wind turbine generator when N=115

4 结 论

当前阻抗模型主要用于给定运行工况下的振荡稳定性分析，难以确定风电接入系统在宽频振荡约束下的关键工况条件，无法直接建立风电接入容量与电网参数的数学关系。针对这一问题，文中建立了风电机组的全工况阻抗模型，分析了输出功率和短路比对风电系统的宽频振荡稳定性的影响，得到了临界振荡稳定时对应的电网短路比，进而分析了宽频振荡稳定约束下的风电接入容量，最后通过时域仿真对分析结果进行了验证。

结果表明：基于全工况阻抗分析方法可有效确定风电机组在不同输出功率和端口电压的条件下，发生振荡的临界短路比，且根据该短路比和电网阻抗，可进一步确定在不同的电网条件下风电的最大接入容量，从而在风电场规划设计阶段消除其并网后的振荡风险，保障系统的安全稳定运行。

目前文中仅考虑风电直接接入交流电网这一场景，而且进行了大量简化，未来可进一步探索其在风电经柔直孤岛并网或其他复杂场景中的应用。