面向骨干网流量的非线性组合预测方法
杜秀丽,陶 帆,范志宇,吕亚娜
(大连大学 通信与网络重点实验室,辽宁 大连 116000)
1 引 言
网络流量是记录和反映网络以及用户活动的重要载体,对它的预测能够指示未来网络的运行状况,对增强网络性能、解决网络拥堵、防止网络入侵有着重要的作用.网络流量预测问题定义为:利用某一段历史时刻的流量数据的统计特征以及强时序性的特点进行建模学习,则可以预测未来某一时刻的网络流量.网络流量预测以时间尺度角度划分为大时间尺度和小时间尺度(采样时间间隔小于1秒[1]);以线性特征角度划分为线性模型和非线性模型;以模型数量角度划分为单一预测模型和组合预测模型.
传统线性预测模型如自回归模型(Auto Regressive,AR)、自回归滑动平均模型(Auto Regressive Moving Average,ARMA)、差分自回归滑动平均(Auto Regressive Integrated Moving Average,ARIMA)模型等不能全面反映网络流量序列的复杂变化特征,预测准确率比较低.后有学者研究将支持向量机(Support Vector Machines,SVM)[2]、神经网络[3]等机器学习领域理论引入分析流量的非线性特征,虽然比起线性模型,非线性预测模型更能够捕捉动态的、复杂的网络流量特征,预测精度有所提高,但预测方法仍然有各自的局限性如SVM的关键参数难以寻找,神经网络易陷入局部最小值等.
在单一预测模型不断研究的基础上,为了利用不同模型的优势提取更丰富的特征信息,大量的学者开始研究组合模型.Lu S等人[4]利用ARIMA模型预测较为平稳的线性流量信息,同时利用长短期记忆循环神经网络(Long Short Term Memory,LSTM)模型预测非线性变化的流量信息;而Liu B等人[5]则进一步将LSTM神经网络改进并与ARIMA模型进行组合;Guo J等人[6]利用支持向量机回归(Support Vector Regression,SVR)和LSTM各自的优势,将二者进行合理组合,最后利用基于滑动窗口的动态加权方法将预测结果进行融合从而提升了模型的预测能力;Abien Fred M.Agarap等人[7]利用门控循环单元和SVM模型进行组合后实现网络流量预测.赵建龙等人[8]针对网络流量的非线性和多维度动力学特性,先利用小波对流量进行多尺度分析,其次将SVR与ARIMA组合预测网络流量.
以上组合模型均是以大时间尺度的网络流量预测模型,虽然预测精度较为理想,但所使用的时序预测方法LSTM及其变体只能对流量数据单向学习,未能充分学习非线性特征信息.而在骨干网中,短期预测比长期预测更有实际意义[9],对骨干网的流量预测的建模分析需要从大时间尺度转移到小时间尺度上来[10],同时网络结构的复杂化使得流量组成及构造产生巨大的改变,需要对非线性预测方法进一步深入研究.
综上所述,为了充分挖掘骨干网流量数据的非线性特征,进一步提高小时间尺度下网络流量预测的准确性,本文提出一种基于灰狼优化支持向量机和双向长短期记忆循环神经网络组合模型的网络流量预测方法.双向长短期记忆循环神经网络(Bi-directional Long Short Term Memory,BiLSTM)对网络流量数据进行双向学习同时利用灰狼优化算法(Grey Wolf Optimizer,GWO)对SVM的关键参数进行寻优避免人为影响.利用优化后的SVM得到全局最优解且泛化能力强的优势来改善BiLSTM出现过拟合,易得到局部最优解的问题,最终以组合方法预测结果的残差平方和最小为目标,根据两种方法当前预测结果的误差调整下次的方法权重,动态加权后得到组合方法的预测结果,从而提高网络流量预测的稳定性和准确性.
2 BiLSTM和SVM网络流量预测方法
2.1 基于BiLSTM网络流量预测方法
BiLSTM神经网络[11]是以LSTM神经网络[12]为基础进行改良而来,由正向LSTM和反向LSTM神经网络融合而成.BiLSTM引入了双向学习的思想,使用一个正向LSTM网络和一个反向LSTM网络,分别提取流量序列过去和未来蕴含的信息,按照一定的权重相结合得到预测结果.基于BiLSTM网络流量预测方法训练步骤如下:
Step 1.数据预处理.使用滑动窗口技术处理采集得到的原始网络流量数据,完成归一化和数据划分后,得到网络流量训练集;
Step 2.设定训练目标值与最大训练次数;
Step 3.初始化BiLSTM网络的各个参数;
Step 4.判断训练计数值是否大于设定的最大训练次数,如果大于,执行Step 9,否则执行Step 5;
Step 5.将训练数据输入到BiLSTM中,进行前向计算;
Step 6.正向和反向LSTM网络的输出加权融合得到预测结果;
Step 7.将预测结果与真实值比较,计算预测误差值;
Step 8.若预测误差值小于设定的目标误差值,执行Step 9.否则执行基于时间的反向传播算法更新网络参数值,同时训练计数值加1,返回Step 4;
Step 9.完成对BiLSTM网络的训练.
图1为基于BiLSTM的训练流程图.
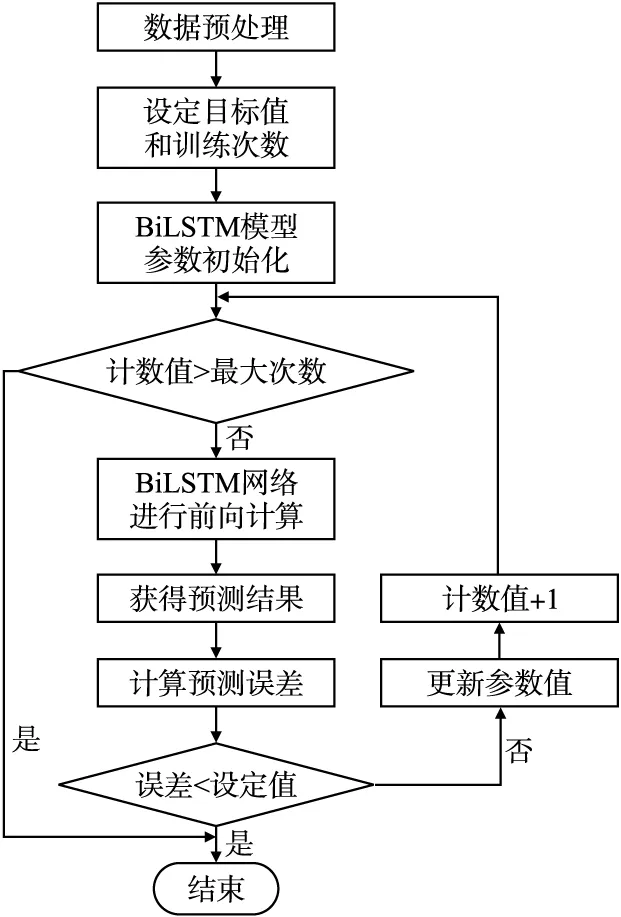
图1 基于BiLSTM的训练流程图Fig.1 BiLSTM training flowchart
2.2 基于GWO-SVM的网络流量预测方法
SVM是一种统计学习理论,依据结构化风险最小的思想进行求解,从而获得全局最优解且泛化能力较强.对于非线性回归预测,SVM通过引入核函数将输入的原始数据从维度较低的空间中映射到维度较高的空间里.本文选用高斯径向基核函数(Radial Basis Function,RBF),如公式(1)所示.
K(xi,xj)=exp(-g(xi-xj)2),(g>0)
(1)
高斯径向基函数下最优超平面回归方程为:
(2)
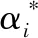
SVM中的惩罚参数C与RBF内部参数g的取值大小影响模型的泛化能力与预测精度,一般情况下参数根据经验设定,这就使得SVM的预测效果容易受到人为因素的影响.为了能够提升模型的泛化能力和预测的准确性,使用作为群体智能算法之一的GWO优化SVM模型[13,14]中RBF的参数g和惩罚参数C.
GWO是由Mirjalili等人在2014年[15]提出的,该算法参数少、结构简单但具有较强的全局搜索能力和收敛性能,广泛应用于无人机路径规划,直流电机最优控制、神经网络参数寻优等最优化问题.GWO算法可以分为3个过程:狼群等级划分、包围猎物和攻击猎物.
1)狼群等级划分
GWO模拟了灰狼狩猎活动,按照社会等级将狼群划分为4层:α等级最高,之后依次为β、δ和ω狼.当狼群对猎物实施包围和发起进攻时,α狼负责带领狼群,β和δ负责协助,ω狼紧随其后.
2)包围猎物
(3)
(4)
(5)
(6)
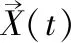
3)攻击猎物
狼群在α狼的指引下搜寻猎物的位置并进行猎杀.通过每次迭代获得α、β和δ狼,并更新其他狼的位置.公式如下:
(7)
(8)
(9)
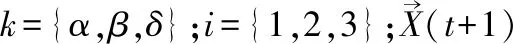
利用GWO优化SVM的算法流程图如图2所示,其步骤如下:
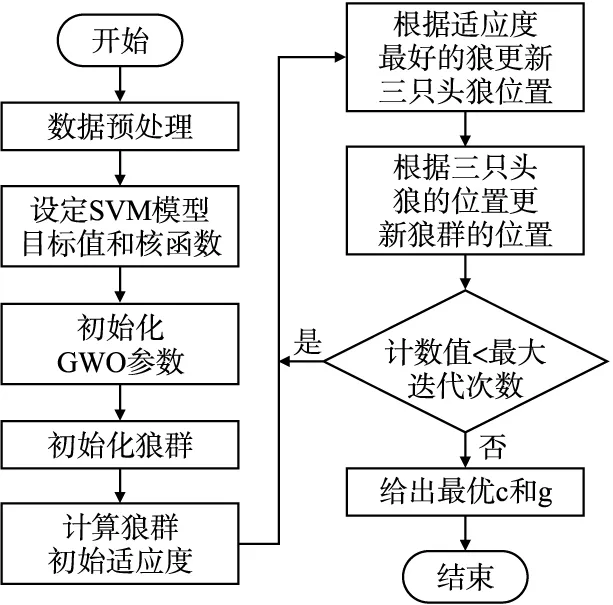
图2 GWO优化SVM的算法流程图Fig.2 Algorithm flow chart of SVM optimized by GWO
Step 1.数据预处理.使用滑动窗口技术处理采集得到原始网络流量数据,完成数据划分和归一化后,得到网络流量训练集;
Step 2.设定训练目标值同时选定SVM所用核函数;
Step 3.初始化参数.灰狼算法的各个参数,包括狼群总体的个数,循环迭代的最大次数,参数边界范围等;
Step 4.初始化狼群.将SVM的C和g转化为狼群个体位置的参数坐标,从而初始化α、β和δ狼的位置和目标函数值;
Step 5.遍历每个狼,如果搜索位置超出了搜索空间,则重新回到搜索空间,同时计算狼群个体初始适应度,适应度函数为SVM预测值与真实值的平均均方误差;
Step 6.根据适应度最好的狼所在位置进一步调整更新3只头狼,同时根据3只头狼最新的位置对狼群所在的位置进行优化;
Step 7.如果迭代次数小于设定的值,返回Step 5.否则输出最优的C和g.
将最优的C和g带入得到最优SVM并用训练集进行训练.
3 基于GWO-SVM和BILSTM组合模型的网络流量预测
3.1 模型组合方式
为了能够发挥基于GWO-SVM和BiLSTM组合模型的优势,需要合理的设置组合模型中GWO-SVM和BiLSTM各自的权重,从而达到最佳组合的效果.当组合模型中的某种预测模型的均方误差越小时,则该模型在组合模型中所占的权重比例就越大,反之则越小,这种思路可以充分利用不同预测模型得到的预测结果,同时去掉无用的信息[16].组合模型的公式如下:
(10)
(11)
(12)
(13)
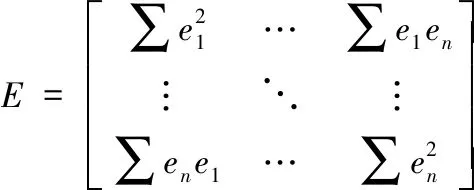
(14)
公式(14)中V=[1,1,…,1]T,将拉格朗日乘子η引入,求解可得:
Q=WTEW+η(VTW-1)
(15)
为了能够得到最优解,对变量W求取一阶偏导可得:
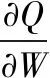
(16)
将VTW=1代入公式(16)可得:
(17)
将结果代入公式(16)可得最优解为:
(18)
在此基础上,本文将GWO-SVM和BiLSTM两种方法组合后进行预测,因此有:
(19)
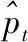
(20)
3.2 基于GWO-SVM和BiLSTM组合预测方法
本文提出的基于GWO-SVM和BiLSTM组合预测方法,在利用BiLSTM神经网络进行预测的同时,利用优化的GWO-SVM方法同步进行预测,以组合方法预测结果残差平方和最小为目标,依据两种方法当前预测误差调整下次的方法权重,动态加权后得到组合方法的预测结果.基于GWO-SVM和BiLSTM组合预测方法框图如图3所示.
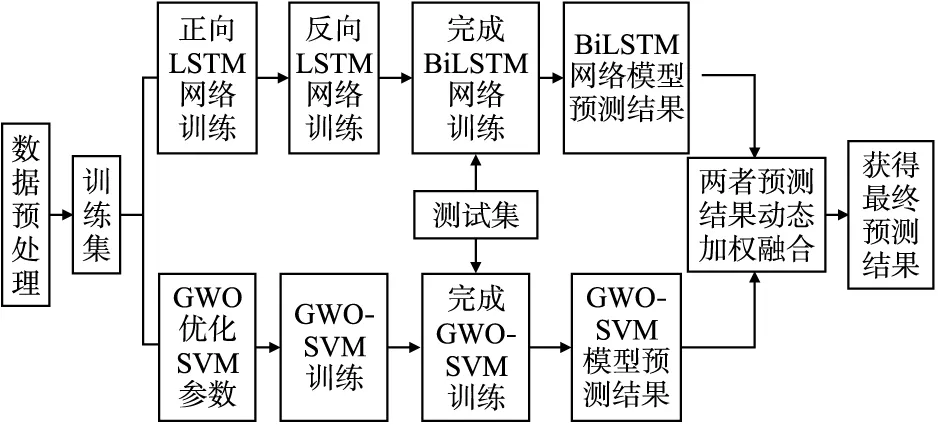
图3 GWO-SVM和BiLSTM组合预测方法框图Fig.3 GWO-SVM and BiLSTM combination method block diagram
基于GWO-SVM和BiLSTM组合预测方法分为训练和预测两个阶段.
训练阶段:分别对BiLSTM和GWO-SVM进行训练,详细训练过程如1.1和1.2所表述.
预测阶段具体步骤如下:
Step 1.数据预处理.使用滑动窗口技术处理采集得到的原始网络流量数据,完成数据划分和归一化后,得到网络流量测试集;
Step 2.将测试集数据输入到BiLSTM中进行前向计算并同时输入到GWO-SVM中;
Step 3.分别得到BILSTM和GWO-SVM预测结果;
Step 4.根据BILSTM和GWO-SVM各自当前的预测结果误差计算下次的各自权重值,进行动态加权;
Step 5.得到最终的预测结果.
4 实验对比与仿真分析
4.1 实验数据与环境
MAWI[17]流量数据数据库主要在WIDE骨干网上对网络流量进行测量分析,记录了日本和美国之间跨太平洋国际光缆上持续15分钟的日常流量,本实验从该数据库的子数据库采样点F下载了2019年1月1日到1月8日的.pcap格式流量数据,使用Wireshark软件,依照时间间隔1s和0.1s分别提取和统计每天的网络流量数据.选用长为60,宽为1的窗口,设置步长为10,对采集得到的原始网络流量数据进行滑动截取.为了消除网络流量指标之间的量纲影响,对网络流量真实数据进行归一化处理,计算如公式(21)所示.
(21)
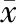
4.2 实验结果与分析
经过大量实验,选定基于GWO-SVM和BiLSTM组合模型预测方法的参数为:狼群数量50,GWO迭代次数200,参数C和g上边界为50,下边界为0.01,SVM选用径向基核函数.BiLSTM网络参数为:输入层神经元60个,隐含层神经元100个,输出层神经元10个,学习速率0.001.初始模型权重值均为0.5,之后根据BiLSTM和GWO-SVM预测结果的误差值动态调整下次的权重值.
在1s和0.1s两个时间尺度的数据集下,分别选用3500组样本数据训练本研究所提方法GWO-SVM-BiLSTM与GWO-SVM、LSTM、BiLSTM,在测试集上分别连续预测500组数据对比其预测结果.为了能够更加清楚的看到4种方法的预测效果,选取预测结果的局部片段进行放大分别如图4和图5所示.
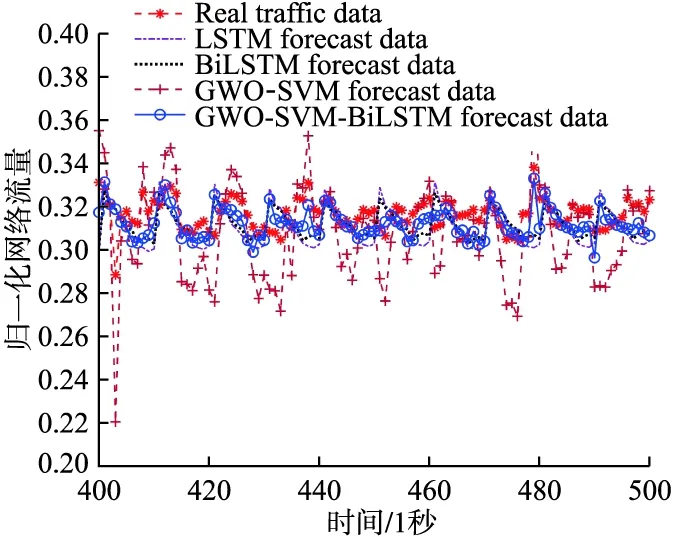
图4 1s时间尺度下测试集上局部预测结果Fig.4 Local prediction results on the test set under the 1s time scale
从图4与图5中可以看出GWO-SVM方法的预测值相比真实值起伏较大,预测效果最差;LSTM方法的预测值相对比较平稳,预测效果强于GWO-SVM方法;BiLSTM方法果对网络流量进行双向学习,其预测值更加收敛于真实值,预测效果强于LSTM方法;本文所提出的GWO-SVM-BiLSTM组合预测方法,克服了单一模型的固有缺陷,相比于其他几种预测方法,可以更加准确的进行网络流量预测.
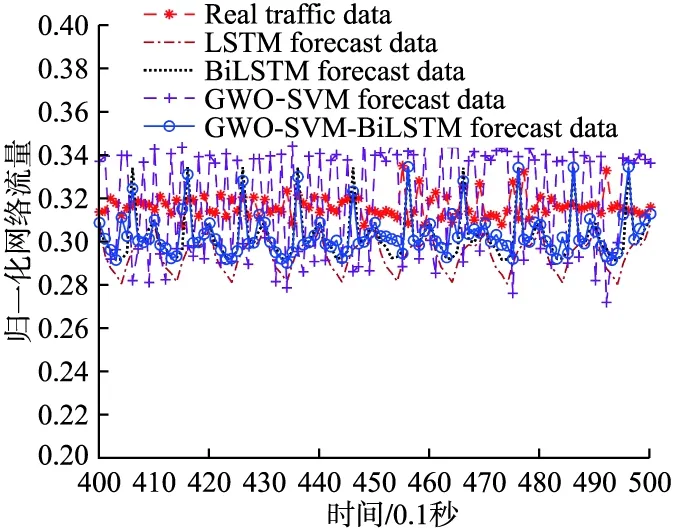
图5 0.1s时间尺度下测试集上局部预测结果Fig.5 Local prediction results on the test set under the 0.1s time scale
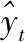
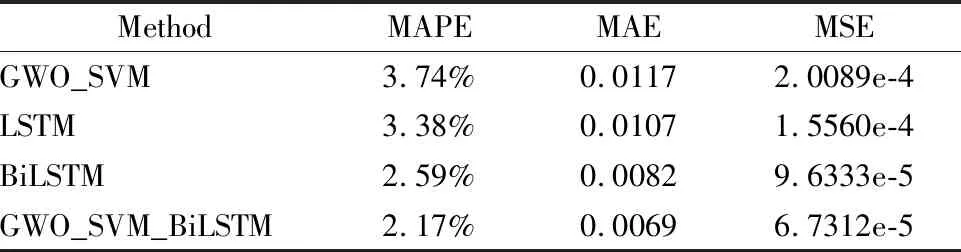
表1 1秒时间尺度下网络流量预测结果Table 1 Test set prediction results on the 1 second time scale

表2 0.1秒时间尺度下网络流量预测结果Table 2 Test set prediction results on the 0.1 second time scale
(22)
(23)
(24)
通过对比多个时间尺度下,不同预测方法的评价指标后可以看出,GWO-SVM方法预测效果最差;LSTM方法预测效果强于GWO-SVM方法;BiLSTM方法充分利用了网络流量的双向特征,在单一模型预测方法中预测效果最好;而本文所提出的GWO-SVM-BiLSRM组合预测方法,在所有预测方法中效果最好.与单一模型预测方法相比较,最终预测结果MAPE值提升了0.5%,MAE和MSE相比原算法提升了15%和30%.
5 结束语
本文针对骨干网流量多变复杂的情况,为了提高网络流量预测的准确度,提出基于GWO-SVM和BiLSTM的网络流量非线性组合模型预测方法,该组合方法结合二者优势:GWO-SVM易取得全局最优解且具有较强的泛化能力;BiLSTM善于处理非线性问题且容错能力强.以组合模型预测结果残差平方和最小为目标,根据预测误差调节模型权重,动态加权后得到组合模型的预测结果.从实验结果可以看出,基于GWO-SVM和BiLSTM的组合模型预测方法优于现有的SVM预测方法,LSTM预测方法以及BiLSTM预测方法,但是组合模型预测方法较为复杂且参数较多,对设备的要求相对更高,同时对资源的占用也更大.

