Assessing Criteria Weights by the Symmetry Point of Criterion(Novel SPC Method)-Application in the Efficiency Evaluation of the Mineral Deposit Multi-Criteria Partitioning Algorithm

Zoran Gligor,Milo Gligori,Igor Miljanovi,Suzana Lutovac and Aleksandar Milutinovi

Faculty of Mining and Geology,University of Belgrade,Belgrade,11 000,Serbia

ABSTRACT Information about the relative importance of each criterion or the weights of criteria can have a significant influence on the ultimate rank of alternatives.Accordingly,assessing the weights of criteria is a very important task in solving multi-criteria decision-making problems.Three methods are commonly used for assessing the weights of criteria:objective,subjective,and integrated methods.In this study,an objective approach is proposed to assess the weights of criteria,called SPC method(Symmetry Point of Criterion).This point enriches the criterion so that it is balanced and easy to implement in the process of the evaluation of its influence on decision-making.The SPC methodology is systematically presented and supported by detailed calculations related to an artificial example.To validate the developed method, we used our numerical example and calculated the weights of criteria by CRITIC, Entropy,Standard Deviation and MEREC methods. Comparative analysis between these methods and the SPC method reveals that the developed method is a very reliable objective way to determine the weights of criteria.Additionally,in this study,we proposed the application of SPC method to evaluate the efficiency of the multi-criteria partitioning algorithm.The main idea of the evaluation is based on the following fact:the greater the uniformity of the weights of criteria,the higher the efficiency of the partitioning algorithm.The research demonstrates that the SPC method can be applied to solving different multi-criteria problems.

KEYWORDS Multi-criteria decision-making; weights of criteria; symmetry point of criterion; mineral deposit; partitioning algorithm;performance evaluation

Nomenclature

1 Introduction

Multi-criteria decision-making (MCDM) refers to ranking the given set of alternatives with respect to the given set of criteria.Assessing the weights of criteria is a very important phase in most MCDM models. The assessment of the weights of criteria significantly influences the final rank of alternatives.Various methods have been developed to determine the weights of the criteria.The process of the criteria weight determination plays a key role in every multi-criteria decision-making(MCDM)problem.The high impact of the criteria weights is directly reflected on the final ranking i.e.,optimal final decision.Generally,methods for criteria weight determination are divided into three groups,such as subjective weighting methods,objective weighting methods and combined weighting methods.

Many authors have used objective weighting methods to obtain the final ranking of alternatives.Krishnan et al.[1]developed a modified procedure of the CRiteria Importance Through Intercriteria Correlation(CRITIC)method,called the Distance Correlation-based CRITIC(D-CRITIC)method.They applied five smartphone models to evaluate the criteria weights by D-CRITIC. The obtained results were compared with four other objective weighting methods and analyzed by three different tests to validate the performance of the D-CRITIC method.et al. [2] presented a new way for modification of the CRiteria Importance Through Intercriteria Correlation (CRITIC) method,called CRITIC-M. The modification was composed of two approaches. The first referred to the normalization technique of the initial data and the second to the expression for determining the final values of the criteria weights.Cavallaro et al.[3]proposed a fuzzy multi-criteria model for combined heat and power (CHP) systems selection. The developed model was based on a fuzzy Shannon’s entropy method to compute the objective weights of the criteria while a fuzzy Technique for Order of Preference by Similarity to Ideal Solution(TOPSIS)method was applied for the final ranking of the alternatives(CHP technologies).Wang et al.[4]presented a sustainable battery supplier selection for battery swapping stations based on MULTIMOORA method with uncertainty. The uncertainty was expressed as triangular fuzzy numbers describing the behavior of the input data.The weights of criteria were evaluated by the entropy method.They also performed the verification of the proposed methodology through the sensitivity analysis and comparative analysis with other MCDM methods in a case study in Beijing, China. Chodha et al. [5] utilized the TOPSIS technique to select the best industrial robot for arc welding. The eight possible alternatives (robots) with respect to the five criteria were taken for the final decision. The entropy weighting method was used to denote the objective criteria weights.Vavrek et al.[6]applied three objective weighting methods(Coefficient of variation-CV,Standard deviation-SD and Mean weight-MW)integrated with the TOPSIS method for assessing the efficiency of cultural services in the Czech Republic. They represented 26 theatres(alternatives) related to 11 indicators (technical and financial) to evaluate the efficiency of the theatres. Mukhametzyanov [7] presented three objective weighting methods (Entropy, CRITIC and SD)for criteria weight determination and performed a comparative analysis of them.Vujiiet al.[8]suggested a multi-criteria decision-making method for air conditioner selection. They applied two MCDM methods, MOORA and SAW, to select the best alternative, while the criteria weights were determined by two objective weighting methods, Entropy and CRITIC. The numerical example was expressed through the case study to illustrate a comparison analysis of the combined MCDM methods and objective weighting approaches.Yalcin et al.[9]examined several different measures,such as accounting-based performance (ABP), value-based performance (VBP) and overall performance(OP), to evaluate the performance of initial public offering (IPO) firms in the pre-IPO and post-IPO periods.The VIKOR method was utilized for ranking the IPO firms,while objective weighting methods (CRITIC and MW) were applied to determine the weights of criteria. They displayed the results by case study to validate the performance of 16 Turkish IPO firms. ¸Sahin [10] investigated the material selection problem for a flywheel. The grey relational analysis (GRA), TOPSIS and Organization Rangement Et Synthese De Donnes Relationnelles(ORESTE)method were employed for the final ranking of the materials.The objective weighting methods,SD and CRITIC method,were implemented to establish the significance of criteria.The six approaches based on MCDM methods combined with objective weighting methods were compared and integrated with the Copeland method to choose the best alternative. Wei et al. [11] proposed the extended GRA method for solving the probabilistic uncertain linguistic multiple attribute group decision-making(MAGDM)with unknown attributes (criteria) information. The CRITIC method was used to calculate the objective criteria weights.They were shown a numerical example for site selection of electric vehicle charging stations(EVCS) to verify the developed algorithm. Meiet al. [12] created a new hybrid model based on a combination of the CRITIC and MARCOS methods for the estimation of the logistics performance index in Western Balkan countries. The weights of six criteria were analysed and determined by the CRITIC method and then the five alternatives (Western Balkan countries) were ranked by the MARCOS method. Keshavarz-Ghorabaee et al. [13] developed a novel method for criteria weight determination, namely MEREC (MEthod based on the Removal Effects of Criteria). They showed and described a detailed computational analysis of the MEREC method step by step. They also presented a comparative analysis with other objective weighting methods for the validation of the introduced method’s results through the example. Hadi et al. [14] proposed a combination of the MEREC method and modified TOPSIS method to select the best hospital location for COVID-19 infected patients demonstrated in a real-world case study in Baghdad, Iraq. They showed two main phases of the developed model in which the first phase contains the Internet of Things(IoT)platform represented by geolocation alternatives sites. In contrast, the second phase implements the MCDM techniques represented by a web application system.There are also objective weighting methods that are based on the entropy method,such as Criteria Impact Loss(CILOS)and Integrated Determination of Criteria Weight(IDOCRIW)[15-17].

The subjective weighting methods are widely used to evaluate the importance of criteria in MCDM processes.There are many subjective methods,but only a few will be mentioned in the following literature.Gorcun et al.[18]developed a novel integrated fuzzy model based on fuzzy SWARA and fuzzy CODAS methods for assessing an acceptable road tanker vehicle. They established a set of thirteen criteria and four possible alternatives. Fuzzy SWARA was used to quantify the weights of criteria,while fuzzy CODAS was applied to rank the set of alternatives.Cakar et al.[19]proposed a model for supplier selection in a dairy company based on the fuzzy TOPSIS method.They adopted ten criteria and six supplier cities as a set of alternatives and created an MCDM problem.The weights of criteria were determined by the subjective assessment of the decision-maker using a linguistic approach.The supplier cities(alternatives)were selected by a fuzzy TOPSIS method.Pamuar et al.[20]developed a new subjective weighting method for determining the criteria weights named the Full Consistency Method (FUCOM). Stanujkic et al. [21] proposed a new approach for criteria weights evaluation called PIvot Pairwise RElative Criteria Importance Assessment (PIPRECIA). Kerulien˙e et al. [22]presented a new subjective approach for criteria weight determination, which is known as step-wise weight assessment ratio analysis method(SWARA).Krylovas et al.[23]introduced a novel KEmeny Median Indicator Ranks Accordance (KEMIRA) method for establishing the attribute preferences and to calculate the criteria weights. Besides, the previous mentioned subjective weighting methods,there are some that should be noted,such as AHP[24],Ranking method[25],SMART[26],WEBIRA[27],OPA[28]and many others.

Besides,the objective and subjective weighting methods,combined(integrated)weighting methods take an important place in the process of assessing criteria weights.Many authors deal with these approaches for determining the criteria weights.Odu[29]presented an overview of the basic weighting methods for estimating criteria weights, including a detailed description of the subjective, objective and combined(integrated)weighting methods.Jahan et al.[30]proposed a framework,including all types of weighting methods for material selection problems. They applied objective and subjective weighting methods to develop a novel combined weighting method for criteria weight evaluation.Chen[31]combined AHP and Entropy into one combined weighting method integrated with the TOPSIS method to create an MCDM model for the building material supplier selection.Ali et al.[32]used an integrated weighting method based on a best-worst method (BWM) as subjective and IDOCRIW as objective weighting methods in the decision-making process for power generation technologies selection.Zavadskas et al.[33]combined objective(entropy,CILOS and IDOCRIW)and subjective(experts’attitudes)weighting methods to obtain an overall(integrated)criteria weight.

Bearing in mind these traditional and well-known MCDM methods that are widely applied in different areas, there are many approaches that provide support to decision-makers by integrating all types of weighting methods with other methods under uncertain environments,such as MARCOS[34],MAIRCA[35],RAFSI[36],MABAC[37],MICMAC[38],TODIM[39],picture fuzzy set[40,41],rough set theory[40],neutrosophic set[42,43],intuitionistic set[44],soft set theory[45]and many other extensions of these methods.

As can be seen from the comprehensive literature review,no authors deal with weighting methods for the purpose of evaluating the efficiency of some partitioning algorithm. Specifically, there is no paper to estimate the efficiency of the mineral deposit partitioning algorithm with the help of weight coefficients.These methods are mostly used for the classical determination of the weights of criteria in different real-life problems within the MCDM framework.Guided by that fact,we tried to develop a completely new approach.The paper presents a novel method for objectively defining the weights of criteria.The objective method of determining the weights of criteria helps decision-makers to reduce the subjectivity in that complex task and to increase the accuracy of the final results.It should be noted that this novel method represents a new approach to estimating and analyzing the efficiency of the multi-dimensional partitioning algorithm.For that purpose,the tendency is to balance all dimensions(criteria)to obtain more efficient results from the partitioning algorithm.

The main aim of this study is to present the methodology of assessing criteria weights based on the characteristic of the criterion that is expressed by its symmetry. The developed method belongs to the class of objective methods.Symmetry Point of Criterion(SPC)is used to calculate the weights of criteria. The symmetry point is located in the middle of the interval[a,b],where a and b present the lower and upper value of the criterion, respectively. Measuring the absolute distance from every criterion value to the symmetry point of the criterion,we create the absolute distance vector.The set of these vectors is presented in the form of a matrix of absolute distances.The modulus for a primal matrix element is defined as the ratio of the averaged absolute distance of the criterion to a value of the criterion element.In this way we form the matrix of moduli of symmetry.Averaging every column of this matrix,we obtain row vector,where every element represents the modulus of symmetry of the given criterion.Finally,the weight of the criterion is calculated by dividing every element of the row vector by the sum of the elements.

The application of the developed method is demonstrated to evaluate the efficiency of the mineral deposit partitioning algorithm.This algorithm presents the base for mine production planning.The main objective of the mineral deposit partitioning algorithm is to divide a deposit into a predefined number of parts, and each part should meet the requirements made up by production planners.Usually,these requirements are presented by the elements of the technological vector.The efficiency of the algorithm can be viewed as a multi-criteria decision-making problem.In that context,part of the mineral deposit can be treated as an alternative,while technological requirements are treated as criteria.If we take into consideration that each part should have equal values to the technological requirements(technological criteria),it implies the uniformity of the weights of criteria.Optimal partitioning means the equal values of the weights of criteria.In that case,the entropy of the criteria weights vector has the maximum value.Making the comparison between the entropy of the optimal partitioning and real-life partitioning,we can calculate the efficiency of the algorithm.

In this study,after presenting the theory of the proposed method,we illustrate the method through an artificial multi-criteria decision-making problem. A comparative analysis with three objective weights methods(CRITIC,Entropy,Standard Deviation and MEREC)has also been undertaken in Section 3,and the results show that the SPC method is very efficient in assessing the weights of criteria objectively.The applicability of the SPC method in the solving real-life problems is demonstrated in Section 4,where the efficiency of the mineral deposit multi-criteria partitioning algorithm is calculated by using the entropy of the weights of criteria.Section 5 presents the conclusion.

2 The SPC Method

In this section, a new method based on the Symmetry Point of Criterion (SPC) is proposed for assessing the weights of criteria in any multi-criteria decision-making problem.The SPC method uses the symmetry point of criterion,i.e.,the modulus of symmetry of the criterion to measure its influence on the weights of criteria.A higher value of the modulus indicates a greater weight of the criterion.The following steps are used to estimate the weights of criteria by objective SPC method.

Step 1:Create the decision matrix

Suppose that there are two finite sets,AandC.SetAconsiders available alternatives,while setCconsiders criteria that will be used to assign adequate values to the alternatives.Letmandndenote a total number of alternatives and criteria, respectively. Accordingly, the decision has the following form:

where:

xij-an assessment of alternativeAiwith respect to a set of criteria

m-total number of alternatives

n-total number of criteria

Step 2:Calculate the Symmetry Point of Criterion(SPCj)

In computing the symmetry point of the criterion only extreme values should be considered.LetXi1= {x11,x21,...,xi1}T;∀i∈[1,m]be a column vector ofC1criterion values,with respect to a set of alternatives.If the lower and upper values of the interval[a,b]are defined asa=min{x11,x21,...,xi1}Tandb=max{x11,x21,...,xi1}T, respectively, then the pointc, which is located in the middle of the interval, represents the symmetry point of criterionC1. The common equation for calculation the symmetry point is as follows:

Step 3:Create the matrix of absolute distances

Recall vectorXi1and create new extended vector by inserting anSPC1point at the specified location. For example,Xi1= {x11,x21,...,SPC1,...,xi-11,xi1}T; ∀i∈[1,m] represents an extended vector. Obviously, some values of the criterion are located on the left side of SPC1, and some on the right side. Further, the absolute distance from every criterion value to SPC1should be calculated:{|x11-SPC1|,|x21-SPC1|,...,|xi-11-SPC1|,|xi1-SPC1|}T; ∀i∈[1,m].If we take into consideration a primal decision matrix,then the matrix of absolute distances can be represented in the following way:

Step 4:Create the matrix of the moduli of symmetry

LetDi1={d11,d21,...,di1}T;∀i∈[1,m]be the column vector of the absolute distances concerning criterionC1. The modulus for a primal matrix elementx11is defined as the ratio of the averaged absolute distance of criterionC1to a value of elementTherefore, the matrix of the moduli of symmetry is of the following form:

Step 5:Calculate the modulus of symmetry of criterion

Averaging every column of the previous matrixR,we obtain row vectorQ,where every elementqrepresents the modulus of symmetry of thejthcriterion.VectorQis defined as:

Step 6:The weights of criteria

Finally, in this step, each objective criterion weight is computed using the vector of moduli of symmetry.The following equations are used for assessing the weights of criteria:

Fig.1 shows the flowchart of the SPC method.

Figure 1:The flowchart of the SPC method

3 The Efficiency of the Mineral Deposit Multi-Criteria Partitioning Algorithm by SPC Method

Underground mining experts are faced with an extremely hard task concerning production planning with respect to the technological requirements. Geostatistical methods use data obtained by exploration drilling to create a block model of a mineral deposit. A mineable block is a threedimensional object which can be mined in an economically viable way. Each block is characterized by the following attributes: specified dimensions (for example: 10 m × 10 m × 10 m), ore tonnage(for example: 2200 t), ore grades (for example: 1.75% Lead; 3.79% Zinc), and specifiedx,y,andzcoordinates.

The authors borrowed a mineral deposit partitioning algorithm from Gligoriet al. [46] to evaluate its efficiency through the developed SPC method. A hypothetical example borrowed from Gligoriet al.[46]is analysed in the case study.It represents the multi-criteria partitioning algorithm for a mineral deposit.Our idea and motivation of the new proposed method are directed towards the validation of the developed partitioning algorithm. Since the algorithm divided the mineral deposit into several areas that must meet certain technological requirements,we tried to verify these areas by a new approach based on the objective weighting method.The efficiency of our partitioning algorithm is manifested as a uniform distribution of weight coefficients. The new proposed SPC method has proved that the mineral deposit partitioning algorithm succeeded in dividing the mineral deposit to a very high-level,considering the target values of the multi-dimensionalTMCs.

A mineral deposit can be presented by a finite set of mineable blocksB= {bh}h∈[1,H], whereHis the total number of mineable blocks.Characteristics of the blocks are expressed by an attribute vectorwhereAis the total number of attributes.

On the other hand, a technological mining cut (TMC) is defined as a subset ofB;TMCi=whereldenotes a total number of blocks associated to theithTMC,andNdenotes a total number ofTMCs.Obviously,TMCis a union of mineable blocks(the homogeneous part of a mineral deposit) characterized with respect to a given set of technological requirements. The total number of technological mining cuts equals the number of mining periods (years of mining). Technological requirements are defined by mine planners and can be presented by the vectorwhereKdenotes the total number of requirements. EachTMCcan be described by a mining cut attributeMCAVi= {aic}c=1,2,..,K;∀i∈[1,N], whereKis the total number of attributes, and equals the number of requirements.

The creation ofTMCscan be formulated as a multi-objective optimization problem.To solve this problem,Gligoriet al.[46]developed a multi-criteria clustering algorithm based on the maximization of the similarity between vectorwhereCtehrepresents the required technological vector.A solution of the formulated problem is given in the following form:

Accordingly, we can draw an analogy between the MCDM problem and mineral deposit partitioning.Technological mining cuts can be treated as alternatives and require a technological vector as a vector of criteria.This analogy can be presented by the following decision matrix:

where

zij-a value of theith TMCwith respect to thejthtechnological criteria.

The main idea of the efficiency evaluation of the mineral deposit partitioning algorithm is based on the following theorem:

Theorem:for a discrete uniform probability density functionpon a finite set of the weights of criteriaentropy has the maximum value:

In terms of algorithm efficiency, the theorem can be formulated as: the greater the uniformity of the weights ofcriteria,the higher the efficiency of the partitioning algorithm.It means that the weights of criteria should be equal as far as possible.

Proof:The divergence between two discrete distributionspandqis defined as[47]:

where

p(Wteh)-discrete distribution of the weights of the technological criteria realized by the SPC method.

q(Wopt)-discrete distribution of the optimal weights of the technological criteria.the Shannon equation[48]:

The non-negativity of relative entropy implies that:

Hence,

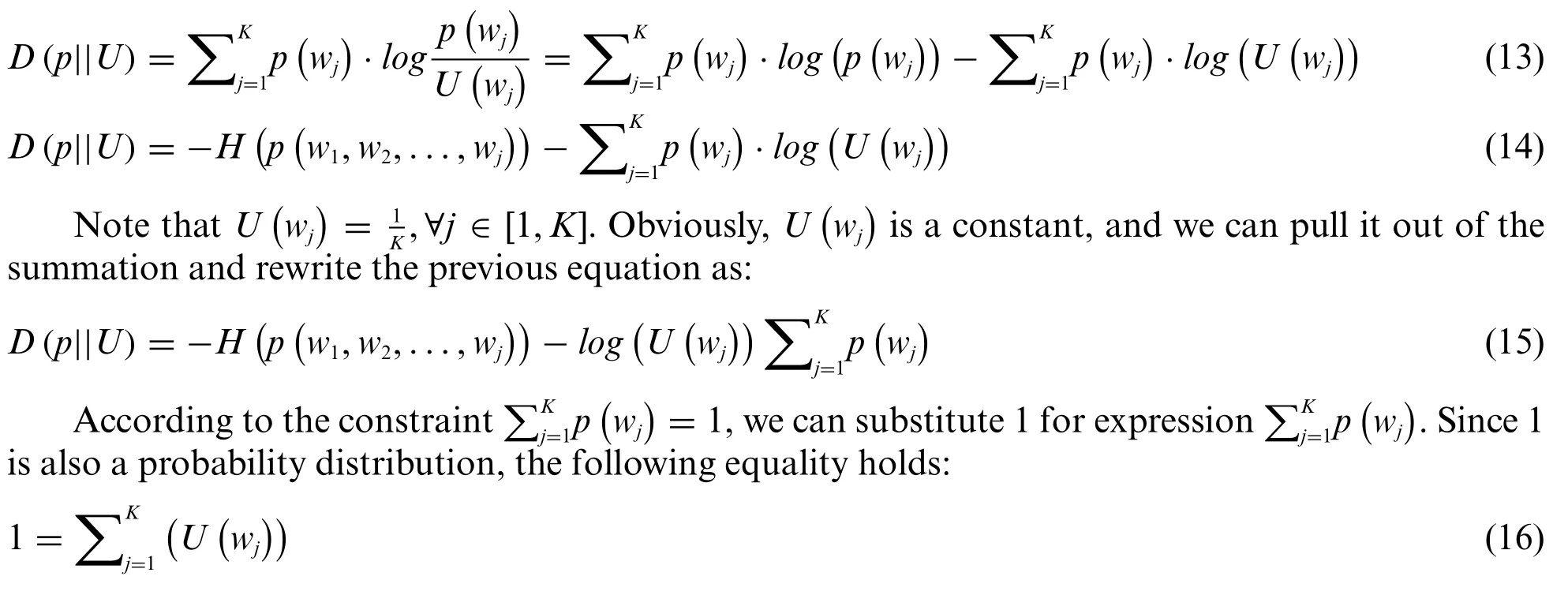
This substitution gives us:

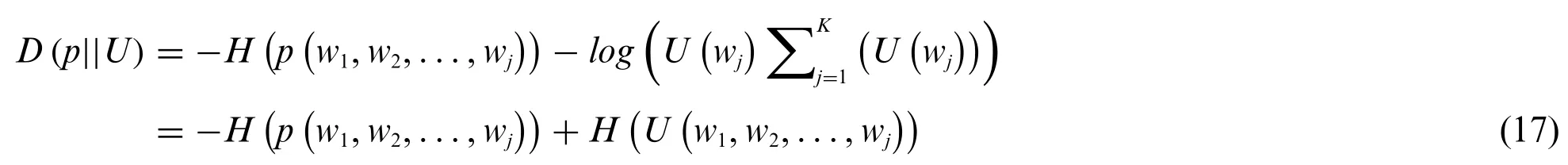
wheredefines the entropy of the uniformly distributed optimal weights of the technological criteria.

According to the above discussion,we have shown that:

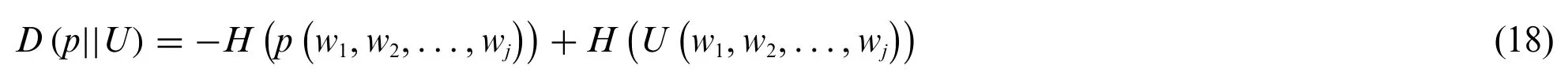
Applying the fact thatD(p||U)≥0 we can conclude that:

If we take into consideration that the probability distribution on[1,K]was arbitrary,the proof is completed.Thus,it means the theorem:“the greater the uniformity of the weights of criteria,the higher the efficiency of the partitioning algorithm”,is valid and can be used to compute the efficiency of the algorithm.

The efficiency evaluation of the algorithm is performed through the following steps:

Step 1:Calculate the weights of criteria by the application of the SPC method over theADMmatrix data,and present them through the following vector:

Step 2:Calculate the optimal values of the weights of criteria as follows:

Step 3:Compute the entropy of the calculated weights.Shannon[48]developed an entropy theory based on thermodynamic that can be interpreted as the quantity of information needed to define the physical state of a system.Entropy can be considered as a measure of the degree of information regularity in weights.The amount of information related to the weights of criteria are calculated using the equations below:

Step 4:Calculate the efficiency of the algorithm(EOA).Discussion about the formulated theorem indicates that entropy of the optimal values of the weights of criteria can be set up as a target value.Based on this,the efficiency of the partitioning algorithm can be calculated as follows:

where

Hteh-entropy of the technological weights of criteria obtained by the SPC method.

Hopt-entropy of the optimal weights of criteria(target value).

Transformation of the numerical values of theEOAto the linguistic variables is presented in Table 1.

Table 1: Linguistic variables for EOA

The required technological vectorCtehis composed of the following components:

-tonnage of aTMC.

-compactness(homogeneous)of aTMC,expressed by Schwartzberg’s index[49];it is defined as the ratio of the square perimeter of the shape to the area.

-standard deviation of the ore grade in aTMCwith respect to the type of a metal hosted in a deposit(%).Ifγ≥2 then deposit is polymetallic.

A brief description of the data needed to execute the partitioning algorithm is presented in Tables 2,3,and Fig.2(for more details see[46]).

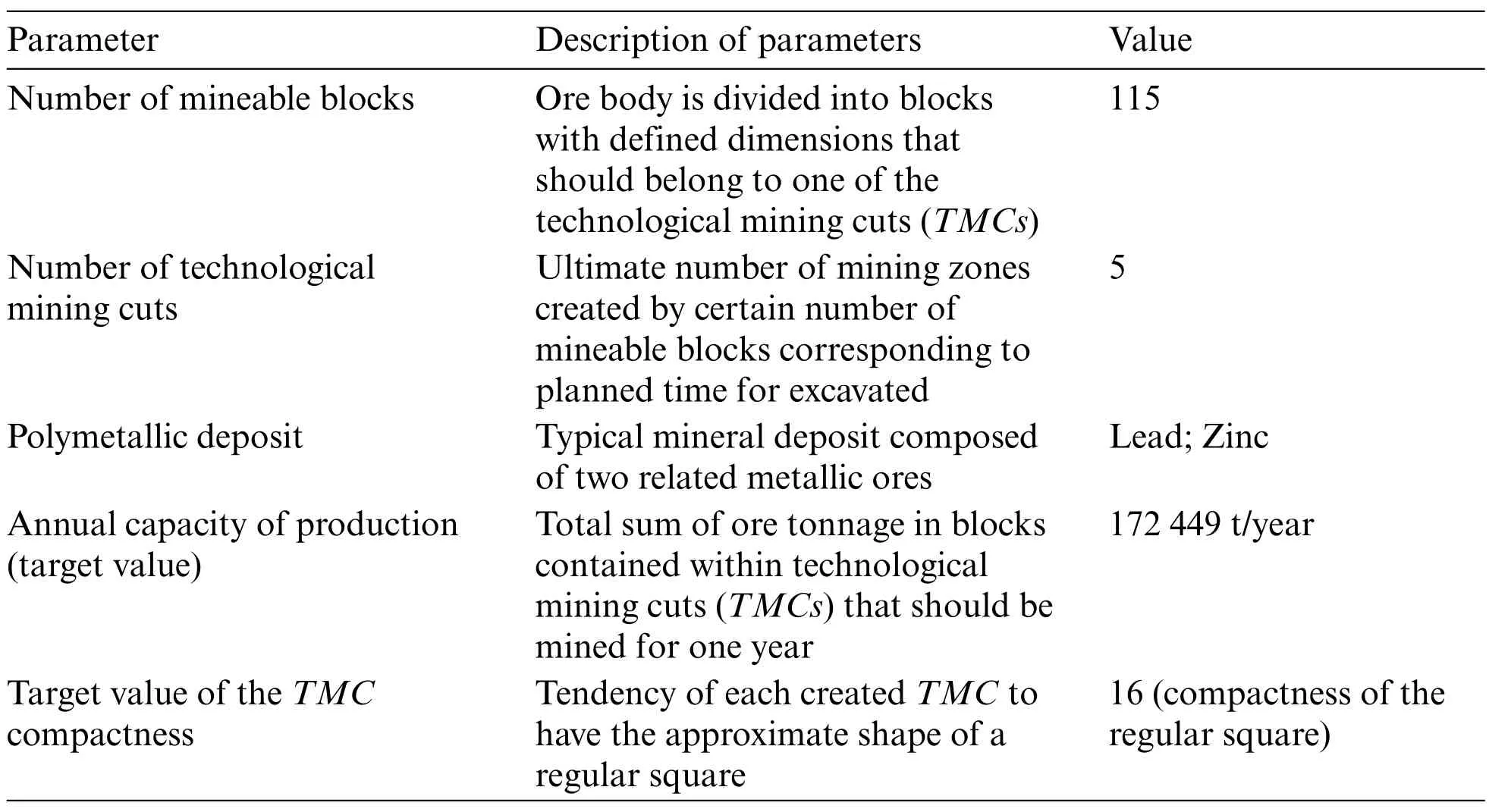
Table 2: Data needed to execute algorithm

Table 3: Tonnage of mineable blocks

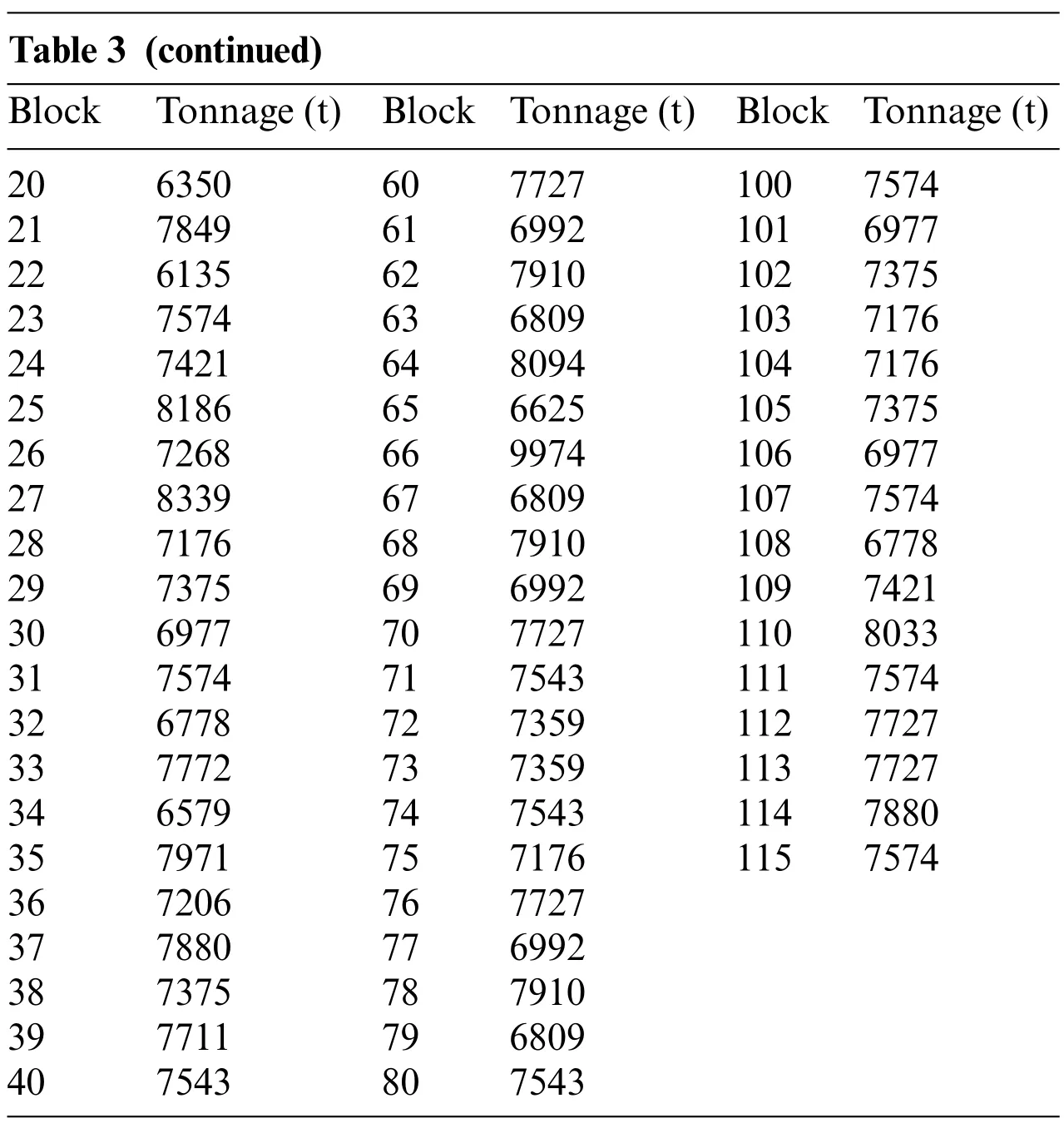
Table 3 (continued)Block Tonnage(t) Block Tonnage(t) Block Tonnage(t)20 6350 60 7727 100 7574 21 7849 61 6992 101 6977 22 6135 62 7910 102 7375 23 7574 63 6809 103 7176 24 7421 64 8094 104 7176 25 8186 65 6625 105 7375 26 7268 66 9974 106 6977 27 8339 67 6809 107 7574 28 7176 68 7910 108 6778 29 7375 69 6992 109 7421 30 6977 70 7727 110 8033 31 7574 71 7543 111 7574 32 6778 72 7359 112 7727 33 7772 73 7359 113 7727 34 6579 74 7543 114 7880 35 7971 75 7176 115 7574 36 7206 76 7727 37 7880 77 6992 38 7375 78 7910 39 7711 79 6809 40 7543 80 7543

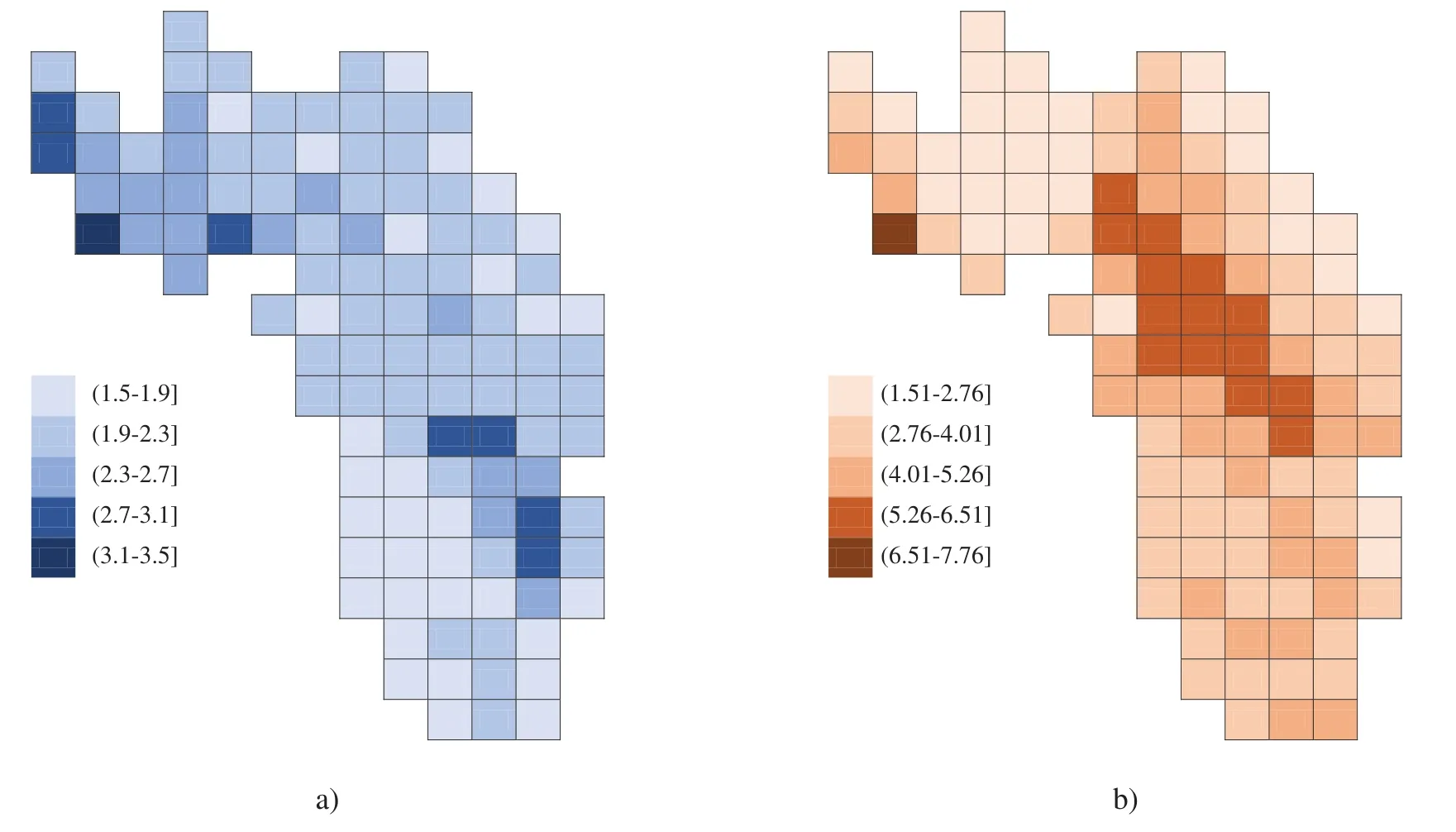
Figure 2:Grade distribution(%):(a)Lead;(b)Zinc[46]

The partitioning algorithm produced fiveTMCswhose characteristics are presented in Table 4,and Fig.3.

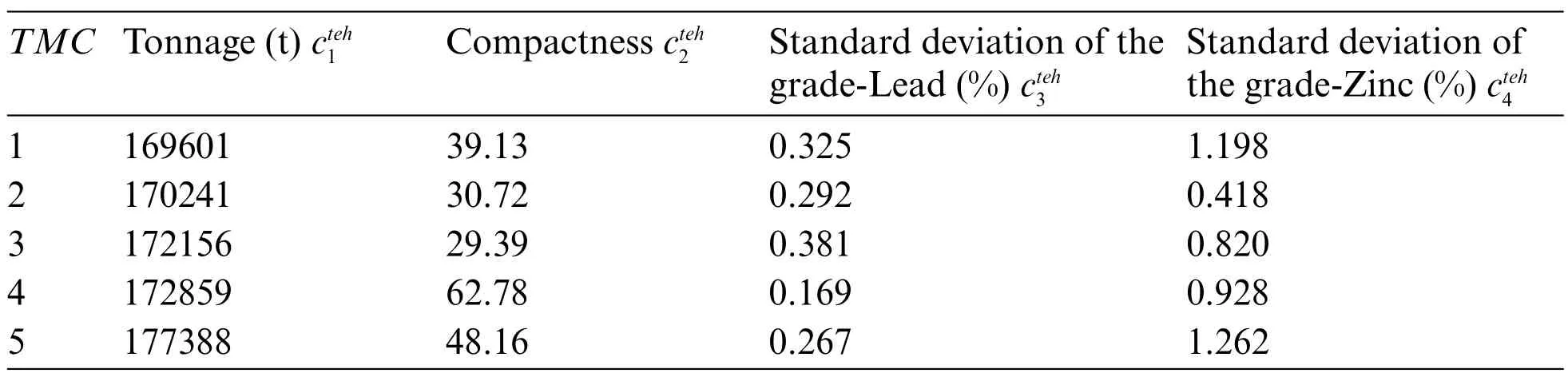
Table 4: Results of the partitioning algorithm

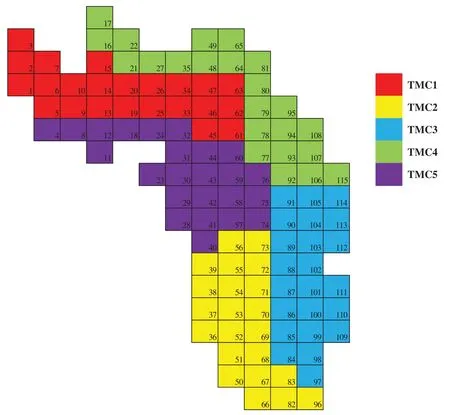
Figure 3:TMCs obtained by the partitioning algorithm[46]

Since the results of the partitioning algorithm obtained in Table 4 meet the technological requirements, they actually represent the values of required technological vectors. Accordingly, theADMmatrix is created in the following form:

The efficiency evaluation of the algorithm is performed through the following steps:

Step 1:The detailed calculation process of the weights of criteria by the SPC method over theADMmatrix is demonstrated Step by Step.

Step 1.1:The elements of an artificial decision matrix are represented as follows:

Step 1.2:The calculation of the symmetry point of each criterion is represented in Table 5.

Table 5: Symmetry point of criterion

Step 1.3:The resulting matrix of absolute distances is as follows:

Step 1.4:Elementsx11andx12of the matrix of the moduli of symmetry are calculated in the following way:

Analogically, we obtain values for the remaining elements, and the matrix of the moduli of symmetry is as follows:

Step 1.5:The modulus of the symmetry of the first criterionC1is calculated as follows:

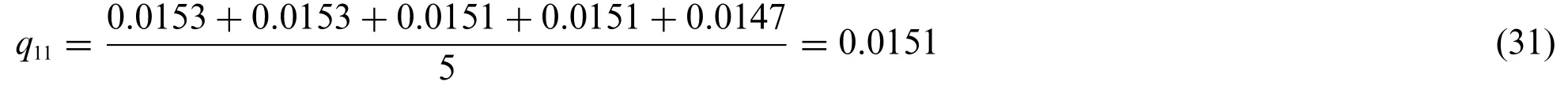
The remaining moduli of symmetry are calculated in a similar way,and values are represented by the following vectorQ:

Step 1.6:Weight of the first criterionC1is:

The weights of criteria for the artificial MCDM problem are shown in Table 6,and Fig.4.

Table 6: The weights of criteria

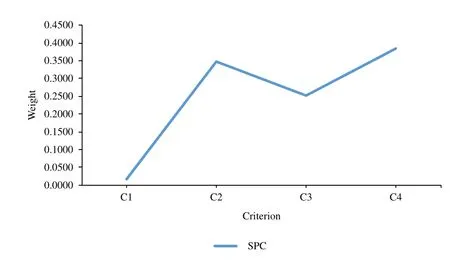
Figure 4:Weights of criteria calculated by the SPC method

Step 2:The values of criteria weights calculated by the SPC method are presented in Table 13.The weights of the optimal criteria are shown in Table 7,and Fig.5.

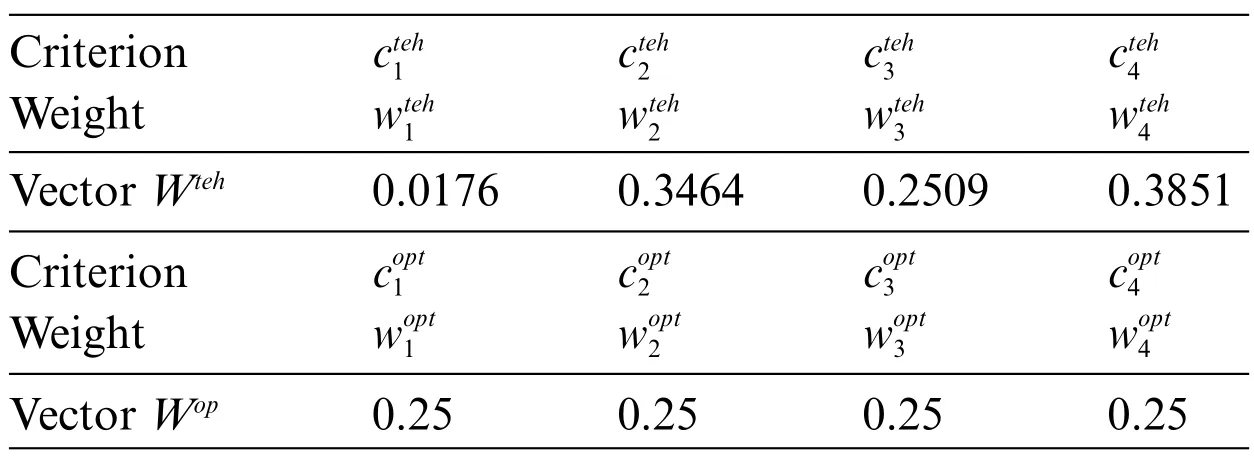
Table 7: The weights of the technological and optimal criteria

Figure 5:Optimal and technological weights of criteria

Step 3:The entropy of the calculated weights and optimal weights is computed as follows:

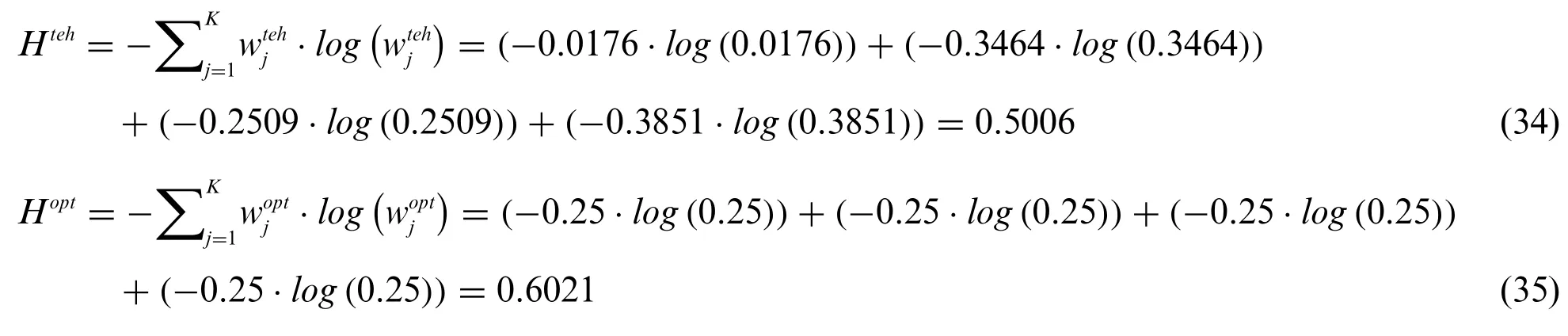
Step 4:The efficiency of the algorithm(EOA)is calculated as:

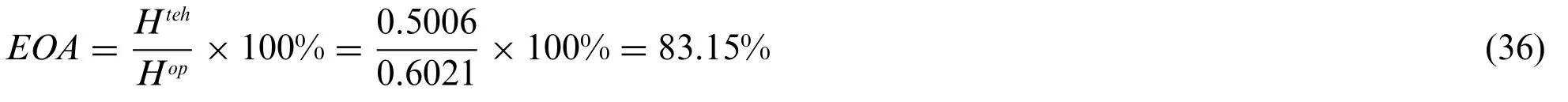
The mineral deposit used in the example can be treated as a very difficult environment for the process of partitioning, with respect to the deposit’s characteristics. The space distribution of ore grades, ore tonnage, and the shape of the deposit are extremely irregular. Bearing in mind the very rigorous technological requirements, it can be said that the mineral deposit partitioning problem is a complex task. Despite this, the algorithm succeeded in dividing the mineral deposit withEOAof 83.15%,i.e.,the efficiency of the algorithm is at a very high level.

4 A Comparison of the Objective Weighting Methods for Determining the Weights of Criteria

This section is related to the comparative analysis to show the capability of the SPC method to define veritable weights of criteria.The proposed SPC method is compared with the most frequently applied approaches for determining criteria weights, such as the CRITIC [7,8,10], Entropy [7,8,50],Standard Deviation [7,10,50] and MEREC [13,14,51] methods. The CRITIC, Entropy, Standard Deviation and MEREC methods used linear normalized decision matrix data to compute the weights of the criteria.

Beside the SD method, the CRITIC and Entropy methods are conventional and widely implemented objective weighting methods that are commonly used for determining criteria weights.These well-known methods are quite simple and easy to understand for decision-makers. Although they require a relatively high level of mathematical calculation, their application is growing constantly.Consequently,weight coefficients obtained by these methods are very reliable and stable.An enormous number of authors have also applied these two methods as a benchmark to compare their new developed methods.Due to these significant specifics,we selected the CRITIC and Entropy methods for comparison with our novel SPC method. In contrast to these usual methods, we have utilized a relatively new objective weighting method for comparison known as the MEREC method.In that way,we obtained an effective verification and validation of our new proposed method.

Our improvement of the CRITIC method involves changing the normalization procedure of the input data. The CRITIC method is quite sensitive to the application of different normalization techniques. The high impact of the normalization of input data is reflected in the final rank of the weight coefficients. Instead of the standard linear max-min normalization technique used in the CRITIC method, we applied linear sum procedure and obtained much better results for criteria weights. Because of these limitations, several authors have developed new modified and extended versions of the classical CRITIC method to improve the final values of weight coefficients[1,2,52].As can be seen from Fig.6 and Tables 9 and 10,the CRITIC method has the lowest degree of correlation with all the applied objective weighting methods.

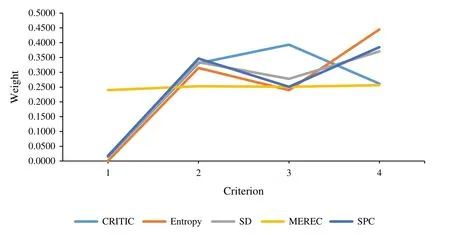
Figure 6:Weights of criteria calculated by methods of comparison

Weights of criteria calculated by these methods are shown in Table 8 and in Fig.6.

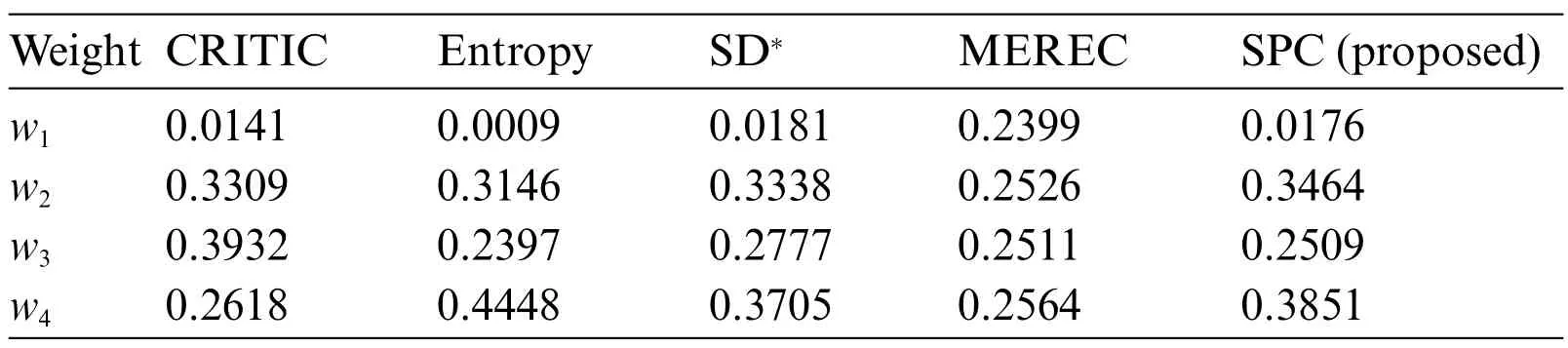
Table 8: Weights of criteria calculated by comparative methods

The Pearson coefficient was used to define the degree of correlation between the weights of criteria computed by the CRITIC,Entropy,Standard Deviation,MEREC and SPC methods.The results of the comparative analysis are presented in Table 9.

Table 9: Comparative analysis results-correlation coefficients

Average correlation coefficients for each method of criteria weighting are shown in Table 10.

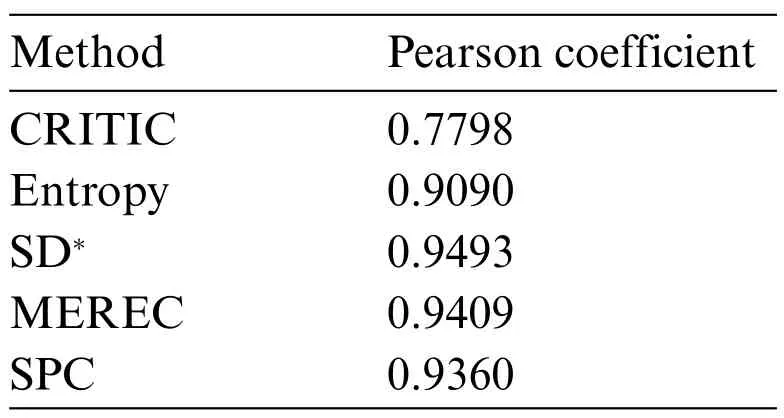
Table 10: Average values of comparative analysis parameters for criteria weights

Rank ordering of the weights of criteria for different criteria weighting methods is presented in Table 11 and Fig.7.

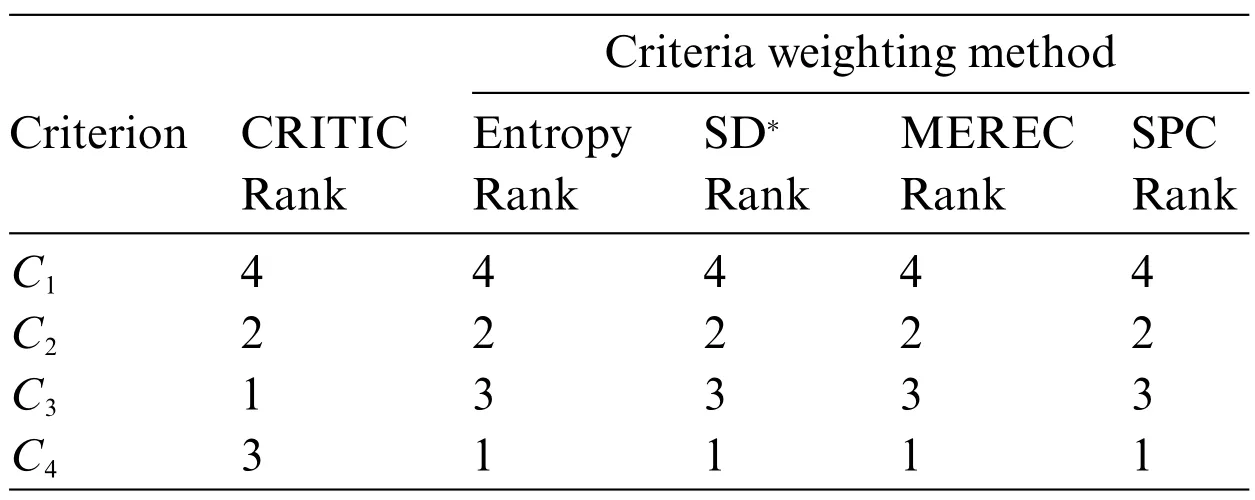
Table 11: Scores for rank ordering of the weights of criteria

Figure 7:Rank order of the weights of criteria

The same approach is used to make a comparative analysis for the rank ordering of the weights of criteria.The comparative analysis results are presented in Table 12.

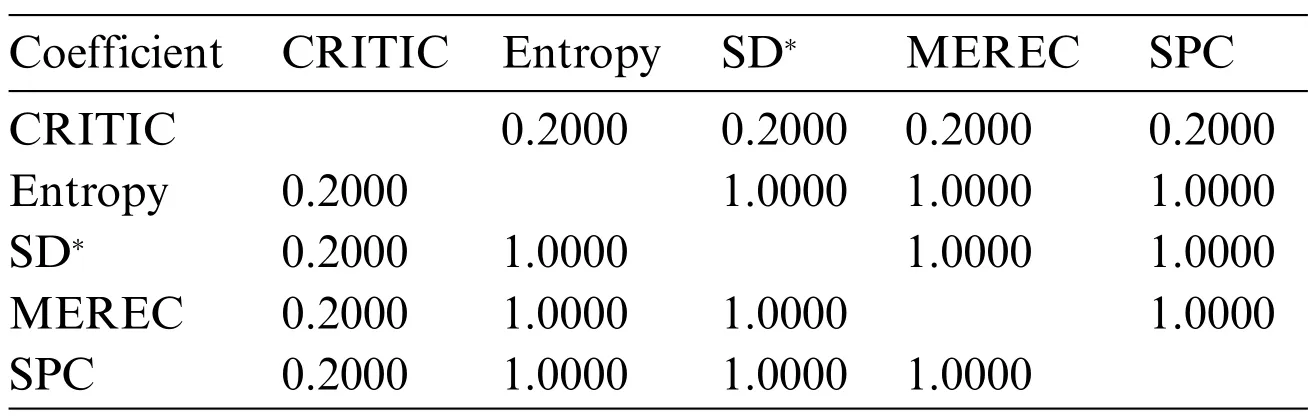
Table 12: Comparative analysis results for criteria weights rank ordering

The average correlation coefficients for each method of criteria rank ordering are shown in Table 13.

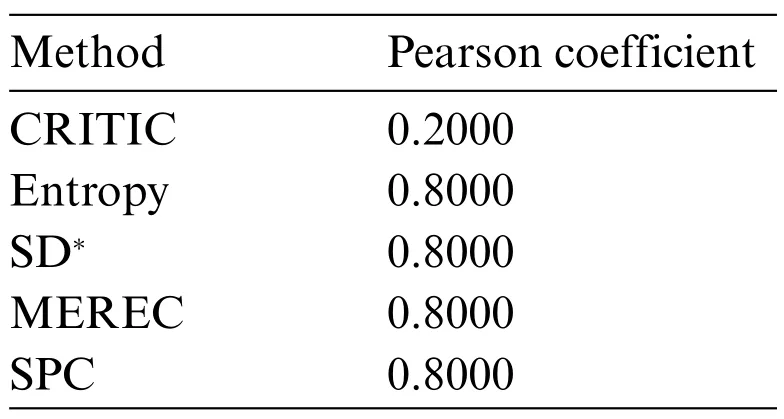
Table 13: Average values of comparative analysis parameters for criteria rank ordering

The values shown in Table 9 indicate the existence of a strong correlation between the weights of criteria assessed by the SPC method and the weights assessed by the Entropy,Standard Deviation and MEREC methods.There is a slightly lower correlation between the SPC,Entropy,SD and MEREC methods on one side compared with the CRITIC method on the other.The average Pearson coefficient of correlation(0.9360;see Table 10)shows that the SPC method stands shoulder to shoulder with the other considered methods.

A comparative analysis using the criteria rank ordering is a more rigorous approach than the previous analysis.In such comparison circumstances,the SPC method showed very acceptable results.The correlation coefficient with the Entropy,Standard Deviation and MEREC methods is extremely high(1.000;see Table 12),while with the CRITIC method it is low(0.2000;see Table 12).The average coefficient of correlation of 0.8000 indicates the high level of applicability of the SPC method.

According to the above discussions,we can say that the SPC method is very capable of assessing the weights of criteria in MCDM problems.Furthermore,all the parameters of comparison showed that the developed method is very reliable.

The efficiency of the algorithm (EOA) by other objective weighting methods that are used for comparison analysis is calculated using the Eq.(24) and the results obtained are shown in Table 14 and Fig.8.

Table 14: Efficiency of the algorithm(EOA)by all objective weighting methods

The efficiency of the algorithm determined by all the applied objective weighting methods is shown in Table 14 and Fig.8. From the obtained results, it is clearly visible that all methods have either a high and or highEOAvalue,according to Table 1.The MEREC method with 99.98%EOAindicates superiority over the other methods, although the weights of criteria are not graphically matched to other methods as can be seen from Fig.6. However, the rank ordering of the weights of criteria obtained by the MEREC method has an extremely high correlation with other methods. The SPC method demonstrated the very high value of 83.15%EOArelative to the other methods (CRITIC 82.52%, Entropy 77.41% and SD 83.85% ofEOA). Obviously, SPC is completely competitive with all methods and absolutely applicable in solving such a complex problem providing verification and validation of the partitioning algorithm.

Figure 8:Graphical review of the efficiency of the algorithm

From the extensive comparison analysis, we can highlight two main advantages of the new proposed SPC method. The first advantage is reflected in the fact that this method illustrates a new objective weighting method for defining the weights of criteria. Each MCDM technique should increase objectivity during the decision-making process.Since the attribute importance plays a very dominant role in the decision-making process, this proposed method helps decision-makers to obtain a more objective and reliable final rank of alternatives. The second advantage of the SPC method is expressed through the efficiency evaluation of the mineral deposit partitioning algorithm.This approach presents the novel mechanism for estimating the performance of every partitioning algorithm.It means that a uniform distribution of weighted coefficients indicates the high efficiency of the algorithm.As a very flexible and understandable approach,the SPC method can be extensively incorporated with conventional MCDM techniques for solving different problems.Certainly,the new proposed SPC method can be successfully implemented in numerous spheres of science.In a domain of technical sciences,this method can be applied in electrotechnical,mechanical,civil,traffic,energy and many other sectors of engineering.Beside this wide application in engineering fields,the SPC method can be efficiently used in various areas,such as economic fields,medical disciplines,social problems and even in political sciences.

5 Conclusions,Limitations and Future Research

Every real-life problem contains an important element faced through a decision-making challenge.Sometimes decision-makers must react very quickly in a short period of time and under uncertain conditions.Mining engineers are constantly faced with a huge number of challenges.Every investor and mining company management tends to create an optimal production plan as quickly as possible to begin mining activities. This optimal production plan is recognized as a crucial activity if mining companies are to make a profit in a very risky and volatile environment. The new proposed SPC method can be very useful for mining engineers in forming an optimal production plan. Although this method represents the verification of a previously developed partitioning algorithm, it can be applied as a tool for partitioning the mineral deposits in future studies.

The weights of criteria have a significant influence on the solving of multi-criteria problems.Besides the alternatives ranking method,the objective evaluation of criteria weights is also recognized as a very important activity.Excluding the subjectivity related to the preference of criteria should help in selecting the best alternative,i.e.,in making the best decision.For that purpose,we have developed an objective method called Symmetry Point of Criteria(the SPC method).Basically,this method measures the absolute distance between the criterion value of a range of alternatives and the symmetry point of the criterion.The symmetry point represents the midpoint between two extreme criterion values(minandmaxvalue of the criterion). Every objective method can result in different values of criteria for individual decision-making problems but obtained values should be consistent as much as possible.Comparative analysis between the novel SPC method and the CRITIC,Entropy,Standard Deviation and MEREC methods shows that our method is capable of determining the criteria weights in a very efficient way.The average Pearson correlation coefficient of criteria rank ordering is 0.8000.The reallife applicability of the SPC method is demonstrated in the case of the mineral deposit multi-criteria partitioning algorithm.The efficiency of the algorithm depends directly on the values of the weights of criteria.If the calculated weights are mainly uniformly distributed,then the efficiency of the algorithm is higher.

The limitations of the proposed method are as follows.First of all,a hypothetical example is used to test the efficiency of the mineral deposit partitioning algorithm by the SPC method.Future research should be focused on implementing a real-life case study for testing the performance of the abovementioned partitioning algorithm.Beside this obvious shortcoming,the non-inclusion of uncertainty theories into the initial decision-making matrix with input data is recognized as another limitation of the proposed method.Future research must include many different types of fuzzy,neutrosophic and intuitionistic numbers, creating an uncertain environment, and the final ranking of alternatives will be obtained under more reliable conditions.It is possible to interpret the limitations of the case study as follows. Firstly, only the basic attributes (four technological criteria) that characterize a mineral deposit are considered for the partitioning algorithm of the mineral deposit in this case study. In future works, there is a possibility to increase the number of criteria and test the efficiency of the partitioning algorithm by this proposed SPC method. Secondly, one of the key attributes that must meet the technological requirements is ore grade.Since the standard deviation is used to calculate ore grade,involving fuzzy numbers in the process of calculating the standard deviation of the ore grade is a very difficult and complex task.Future work can be directed towards overcoming this problem in the calculation process of standard deviation under a fuzzy environment by developing software for that purpose.

If we take into consideration that many real-life multi-criteria decision-making problems are burdened by uncertainties,then future research will be directed to including them in the SPC method.We will also explore how the developed method behaves in such environments.An extended version of our paper can be performed by introducing the stochastic diffusion process for the purpose of describing the features of some criteria.In that way,we can develop a dynamic model that is capable of solving more complex problems in the real world.Another variant of upgrading the paper should be related to integrating the SPC method with other MCDM processes.Certainly,there is potential to combine our developed SPC method with other subjective and objective weighting methods producing a new hybrid approach for calculating the weights of criteria.

Funding Statement:The authors received no specific funding for this study.

Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.