Metric Identification of Vertices in Polygonal Cacti

Xiujun Zhang,Muhammad Salman,Anam Rani,Rashna Tanveer,Usman Ali,＊and Zehui Shao

1School of Computer Science,Chengdu University,Chengdu,China

2Department of Mathematics,The Islamia University of Bahawalpur,Bahawalpur,Pakistan

3Centre for Advanced Studies in Pure and Applied Mathematics,Bahauddin Zakariya University,Multan,Pakistan

4Institute for Intelligent Information Processing,South China Business College of Guangdong University of Foreign Studies,Guangzhou,China

ABSTRACT The distance between two vertices u and v in a connected graph G is the number of edges lying in a shortest path(geodesic)between them.A vertex x of G performs the metric identification for a pair(u, v)of vertices in G if and only if the equality between the distances of u and v with x implies that u = v(That is,the distance between u and x is different from the distance between v and x).The minimum number of vertices performing the metric identification for every pair of vertices in G defines the metric dimension of G.In this paper,we perform the metric identification of vertices in two types of polygonal cacti:chain polygonal cactus and star polygonal cactus.

KEYWORDS Metric;metric identification;metric generator;metric dimension;cactus graph

1 Introduction

The metric dimension is used in a variety of scientific disciplines,including chemical graph theory and computer networking.A technique for finding a vertex’s precise location or position in a network is called localization.In a work environment,localization is used when a computer sends a printing command to help locate nearby printers,broken equipment,network intruders,illegal or unauthorised connections, and wandering robots. The localization of a network is a difficult, expensive, timeconsuming, and arduous procedure. The minimum number of vertices (the metric dimension of a graph representing the network) is picked in such a way that, with the aid of selected vertices, the location of the required vertex may be identified by its distinctive representation.

In robotic engineering,there is no concept of direction and no visibility on a polygonal type planar surface/mesh.So handling the navigation of a robot(a navigation agent)from point to point is a crucial task,which can be done quickly with the help of distinctively labelled landmarks.These landmarks help the robot locate itself on the surface(or graph).The visual detection of a landmark sends information to the robot about its direction,allowing it to determine its position.In this way,the robot’s position on the graph can be determined by its distances to the elements of the set of distinctively labelled landmarks.The problem of locating the fewest number of landmarks to determine the robot’s position is equivalent to finding a minimum metric generator of the graph on which the robot’s navigation is required[1].

Consider a connected graphG=(V(G),E(G)),whereV(G)andE(G)represent vertex set and edge set ofG,respectively.The distance,d(ν,w)between verticesν,w∈V(G)is the length of a shortest path betweenνandw. We use the notationu～νto indicate that the verticesuandνare adjacent inG.

A vertexxidentifies two distinct verticesν,w∈V(G)ifd(x,w)d(x,w).The metric vector of a vertexν∈V(G)with respect to an ordered setW={w1,w2,...,wκ}⊆V(G),is theκ-ordered tuple

The setWperforms the metric identification of verticesxandyinGif and only ifmW(x)=mW(y)impliesx=y.A set of vertices,performing the metric identification ofG,is called a metric generator forG. The minimum cardinality of a metric generator forGis called the metric dimension ofG,symbolized bydim(G)[2,3].

Slater introduced the concept of metric identification by using the concept of metric generator with name reference (locating) set [3]. Since that, this concept was studied independently, by Melter and Harary where they used the terminology of resolving set for metric generator[2].While working on the idea of navigating long range aids,Slater examined the usage of the concept of metric identification in 1975[3].Moreover,it has been described in[1,4]that how the navigation of robots and likely objects can be performed with this concept.The following short survey will develop the interest of relevant researchers working with the problem of metric identification for various graph families:

• Some fundamental problems related to the metric identification in tree graphs and graphs having minimum and maximum metric dimension have been addressed in[4].

• Using an algorithmic technique with mathematical induction,the problem of metric identification has been solved for a family of 3-regular circulant graphs by Salman et al.[5],and for two 4-regular families of circulant graphs by Khalid et al.[6].

• For three families,P(2n,n-1),P(n,4)andP(n,3),of well-known generalized Petersen graphs,the metric identification problem has been solved in[7-9],respectively.

• The study of metric identification has also been taken into account for various chemical networks such as for chordal ring networks in[10](the authors used the algorithmic technique),for silicate networks in [11], for torus networks in [12] and for two hexa chemical networks in[13].

• Various graph products have also been considered in the context of metric identification problem such as the lexicographic product in [14], the cartesian product in [15,16], and the corona product in[17].

The following theorem provides the minimum metric dimension for a connected graph:

Theorem 1.1.[1,4]LetGbe a connected graph,thendim(G)=1 if and only ifGis a path graph.

A connected graph in which no edge is a part of more than one cycle is called a cactus graph,see Fig.1. A cycleCκof lengthκis called aκ-polygon. If each edge in a cactus graph is a part of aκpolygon,then the cactus is called aκ-polygonal(or simply polygonal)cactus.IfCκcontains precisely one cut-vertex, thenCκis called a pendent polygon. Otherwise,Cκis called a non-pendent polygon[18].An induced subgraph of ajthκ-cycleCκin a polygonal cactus obtained by deleting its cut(vertex)vertices will be called ajth blockBjin the cactus.Two distinct verticesxandyin a polygonal cactus are said to be block-wise distance similar(in short BDS)if the distance ofxandyis same with all the vertices of at least one block of the cactus.We label the vertices of a polygonal cactus as follows.

Figure 1:Cactus graphs:(a)is polygonal and(b)is non-polygonal

LetVj= {: 1 ≤i≤κ}be the set of vertices injthκ-cycle of a polygonal cactus for 1 ≤j≤n.Then the vertex set of the cactus isThe aim of this paper is to explore the metric identification of vertices in polygonal cacti.We investigate the minimum number of vertices which perform the metric identification in chain and star polygonal cacti. It is worth noticing that the metric identification of certain graphs have been studied[19,20].However,this notion has not been explored for the chain and star polygonal cacti which makes the paper different from the available literature.

2 Chain Polygonal Cactus

A chain polygonal cactus, denoted byTn,κ, is a class of polygonal cactus in which each polygon has at most two cut vertices,wherenis the number ofκ-polygons,known as the length ofTn,κ.

Lemma 2.1.Forκ≥3 withn≥2,ifSis a metric generator forTn,κ,thenSmust contain at least one vertex from both the end blocks ofTn,κ.

Proof.Without loss of generality,suppose thatSdoes not contain any vertex from the first block ofTn,κ.Then for two verticesx,ysuch thatx～ν1andy～ν1(ν1is the cut vertex between first and second polygons ofTn,κ),we havemS(x)=mS(y),a contradiction.

According to the definition, cactus chainTn,κhas exactlyn-2 non-pendent polygons and two pendent polygons.Forn≥3,Tn,3is unique.However,Tn,κis not unique forκ≥4 andn≥3.Hereafter,we define two special classes of cactus chains forκ≥4 andn≥3.

2.1 Tn,κ with Adjacent Cut Vertices

InTn,κ,if we let=νj(a joint/cut vertex betweenjth and(j+1)th polygons/cycles)for 1 ≤j≤n-1,then cut vertices inTn,κare adjacent,and this type of chain polygonal cactus is denoted byHn,κ.In fact,cut-vertices inHn,κ,lying in the same non-pendent polygon,are adjacent.See Fig.2.

Figure 2:A 4-polygonal chain cactus with adjacent cut vertices

Lemma 2.2.Forκ,n ＞3,it is not possible that two consecutive blocks do not contribute to form a metric generator forHn,κ.

Proof.Contrarily, suppose that two consecutive blocksBiandBi+1do not contribute to form a metric generatorSforHn,κ.Then,there are BDSxinBiandyinBi+1and bothxandyare neighbors of the jointνi,such that no vertexs∈Sidentifiedxandy.So,Sis not a metric generator forHn,κ,a contradiction.

Theorem 2.1.Forn≥3,dim(Hn,3)=2.

We can see that all the metric vectors are distinct.So,Wis a metric generator forHn,3,and thereforedim(Hn,3)=2.

Theorem 2.2.For oddκ≥5,dim(H3,κ)=2.

Proof.By Theorem 1.1,only path graph has the metric dimension equals to 1.So,dim(H3,κ)≥2.Further,considerand accordingly metric vectors of the vertices are:

Obviously for every two verticesx,yofH3,κwithxy,mW(x)mW(y). Thus,Wis a metric generator forH3,κanddim(H3,κ)≥2.

Lemma 2.3.For evenκ≥4,ifSis a minimum metric generator forH4,κ,then|S|≥4.

Proof.We contrarily assume that|S| = 3.By Lemma 2.1,Smust contain one vertex from each end block.Let a vertexube taken from the blockB1and a vertexwbe taken from the blockB4.ThenSdoes not contain any vertex from one of the remaining two blocks.Without loss of generality, we suppose thatSdoes not contain any vertex from blockB3,then we have two possibilities:

Hence,our supposition is wrong and|S|≥4.

Theorem 2.3.For evenκ≥4,dim(H4,κ)=4.

Proof.Lemma 2.3 provides the lower bound fordim(H4,κ).

Now, we prove thatdim(H4,κ)≤4. For this, letand we have to show that for any pair(x,y)of vertices inH4,κ,there is always a vertex inSwhich identifies the pair(x,y).For this,we consider three cases:

Case-IWheneverx,ybelong to the same blockBiofH4,κ,then there are two possibilities:

1. Ifxandyare BDS,then a vertex inS,chosen from the blockBi,will identifies the pair(x,y).

2. Ifxandyare not BDS,thend(x,ν)d(y,ν),whereνis the cut vertex of a cycleCi.Thus,d(x,s)d(y,s)for at least one vertexsofSlying in the blockBi+1(or in the blockBi-1).

Case-IIIfx,ydo not belong to the same blockBi,then there are two possibilities:

1. Whenxbelongs to the blockBiandybelongs to the blockBi+1(orBi-1).Ifxandyare BDS,then there is a vertex ofSlying either in the blockBiorBi-1orBi+1,which identifies the pair(x,y).Otherwise,there is always a vertexsinSlying in the block containingxorysuch thatd(x,s)d(y,s).

2. Ifxandydo not belong to the two adjacent blocks,i.e.,x∈Biandy∈Bjforji+1 andi-1,then we always find a vertexwofSlying inBi(orBj)such thatd(x,w)d(w,y).

Case-IIIWheneverxoryor bothxandyis(are)a joint(s),then there are two possibilities:

1. Ifxandyare adjacent,then there is a vertexu∈S,such thatd(x,u)=1+d(y,u)whereuandylie on a same cycle,ord(y,u)=d(x,u)+1 whereuandxlie on a same cycle.Accordingly,uidentifies the pair(x,y).

2. Ifxandyare not adjacent,then there ares1,s2inSsuch thats1,xlie on the same cycleCi(say)ands2,ylie on the a same cycleCj,whereji,i+1,i-1.In this case,boths1ands2identify the pair(x,y),because

d(x,s2)=d(y,x)+d(y,s2)andd(y,s1)=d(x,y)+d(x,s1).

According to all these cases,it can be concluded thatSis a metric generator ofH4,κ.

We suppose thatSdoes not contain a vertex from the blockB2(say).Then there are two vertices,u1in the blockB1andw1in the blockB2,such thatmS(u1)=mS(w1),whereu1～ν1～w1.So,Sis not a metric generator.Thus our claim is true.Now,Smust have at least one vertex from both the blockB2andBn-1,andSmust containm-3 vertices from(n-2)blocks.So,there always exist two consecutive blocks from each and among them no vertex will contribute to form the setS,which is contradiction of Lemma 2.2.

Both the claims provide that our assumption is wrong.HenceSmust contain at leastm-2 more vertices other thanxandy,which implies that|S|≥m.

Possibility 1:Whenr=m,then we always have a vertexs∈Ssuch thats∈Br+1ors∈Br-1andsidentifies the pairp.

Possibility 2:Whenr∈{m,m+1,m-1},then there is a vertexsinSfrom the blockBr(orBm)such thatsidentifies the pairp.

Possibility 3:Whenr /∈ {m-1,m,m+1},then at least one of the following two observations must true:

•Scontains an elementsfrom the blockBr(orBm)such thatsidentifies the pairp.

•Scontains an elementsfrom the blockBr+1(orBm+1)such thatsidentifies the pairp.

Hence,Sis a metric generator forHn,κ.

2.2 Tn,κ with Non Adjacent Cut Vertices

Rn,κdenotes a chain cactusTn,κsuch that the cut-vertices,lying in the same non-pendent polygon ofTn,κ,are not adjacent,see Fig.3.We further classifyRn,κinto three types:

Figure 3:A 5-polygonal chain cactus with non-adjacent cut vertices

With the similar justification proposed for the proof of Lemma 2.2,we have the following result:

Lemma 2.6.Forκ ＞5 andn≥3,it is not possible that two consecutive blocks do not contribute to form any metric generator forRn,κ.

Theorem 2.6.For oddκ≥3,dim(R2,κ)=2.

It can be easily verified that for every pairx,yof distinct vertices,we havemW(x)mW(y).So,Wis a metric generator forR2,κ,anddim(R2,κ)≤2.

Theorem 2.7.For evenκ≥4,dim(R2,κ)=3.

Proof.The proof follows from the following two claims:

Claim I:(dim(R2,κ)≥3)

Suppose contrarily thatdim(R2,κ) ＜3.Since any metric generator forR2,κmust contain a vertex from both end blocks,by Lemma 2.1,dim(R2,κ)≥2.LetS= {x,y}be a minimum metric generator forR2,κ,wherex∈B1andy∈B2.Then,there are two possibilities:

Thus, according to these possibilities,Sis not a metric generator. So, our supposition is wrong anddim(R2,κ)≥3.

Claim II:(dim(R2,κ)≤3)

Let us consider a setof vertices.Then,metric vectors of the vertices ofR2,κwith respect toSare:

It can be seen that all the metric vectors are different,which implies thatSis a metric generator forR2,κ.Hencedim(R2,κ)≥3.

Letu,ν∈V(G)be any two vertices.Then,u,νare called twins if eitherN[u] =N[ν]orN(u)=N(ν).The relation of twins between vertices ofGis an equivalence relation,which partitionedV(G)into classes each of which is called a twin class.A twin class may be singleton[6].The following results are useful tools to identify twins in a graphG.

Lemma 2.7.[6]Ifuandνare twins in a connected graphG,then no vertex,exceptuandν,ofGidentifies the verticesuandν.

Accordingly,we have the following remark:

Remark 2.1.IfUis twin class in a connected graphGwith|U|=l≥2,then every metric generator forGcontains at leastl-1 vertices fromU.

Theorem 2.8.Forn≥3,dim(Rn,4)=n.

Proof.We prove the result with two cases providing lower and upper bounds for the metric dimension ofRn,4.

Case-I(Lower bound)

InRn,4, we obtainntwin classes each of them has cardinality 2. Now, ifSis a minimum metric generator forRn,4,thenSmust contain at least one vertex from each twin class,by Remark 2.1.This implies thatdim(Rn,4)=|S|≥n.

Case-II(Upper bound)

LetS= {: 2 ≤t≤n} ⊂V(Rn,4). Then,Sis a metric generator forRn,4, because all the vertices have distinct metric vectors with respect toSas listed below:

This implies thatdim(Rn,4)≤n.

Lemma 2.8.For evenκ≥6,ifSis a minimum metric generator forR3,κ,then|S|≥3.

Proof.By Lemma 2.1,Smust contain a vertex from both the end blocks ofR3,κ.Suppose that a 2-element setS= {x,y} is a metric generator forR3,κ, wherexlies in the blockB1andylies in the blockB3.We will discuss two possibilities:

d(u2,x)=1+d(ν1,x),d(w2,x)=1+d(ν1,x).

It follows that our supposition is wrong, and no 2-element set is a metric generator forR3,κ. Thus|S|≥3.

Theorem 2.9.For evenκ≥6,dim(R3,κ)=3.

Proof.By Lemma 2.8,dim(R3,κ)≥3.Moreover,dim(R3,κ)≤3,because the setS={}is a metric generator forR3,κdue to the following distinct metric vectors of the vertices with respect toS:

Theorem 2.10.For evenκ≥6,dim(R4,κ)=4.

Proof.LetS= {} ⊂V(R4,κ). Then the metric vector ofwith respect toSis given below:

It can easily verify that all metric vectors are distinct.Thus,Sis a metric generator forR4,κanddim(R4,κ)≤4.

Now,we claim that ifSis a minimum metric generator forR4,κ,then|S|≥4.Suppose contrarily that |S| = 3. By Lemma 2.1,Smust contain one vertex from both the end blocks ofR4,κ. LetS={x,y,z},wherexlies in the first blockB1andylies in the last blockB4.There are two cases to discuss:

1. Ifzlies in the blockB1(orB4),then there exist BDS,u1lies in the blockB2andw1lies in the blockB3withu1～ν2～w1,such thatmS(u1)=mS(w1),a contradiction.

2. Ifzlies in the blockB2(orB3) and, without loss of generality, we suppose thatzlies in the blockB2,then there are two possibilities:

All these possibilities conclude that our supposition is wrong and|S|≥4.Hence,dim(R4,κ)≥4.

Theorem 2.11.Forn≥3,dim(Rn,5)=2.

Proof.By Theorem 1.1, only a path graph has the metric dimension equals to 1. Therefore,dim(Rn,5)≥2.Now,consider a setW={of vertices ofRn,5.Then,metric vectors of the vertices with respect toWare:

For 2 ≤j≤n,

It can easily verify that for each pair of distinct vertices (x,y)inR3,κ,we havemW(x)mW(y).Thus,Wis a metric generator forRn,5anddim(Rn,5)≤2.It completes the proof.

According to the similar reasoning of the proofs of Theorems 2.4 and 2.5 we have the following two results forRn,κ.

For 2 ≤j≤n,

It can easily verify that for every two distinct verticesx,yofRn,κ, we havemW(x)mW(y). It follows thatWis a metric generator forRn,κanddim(Rn,κ)≥2.It concludes the proof.

2.3 Star Polygonal Cactus

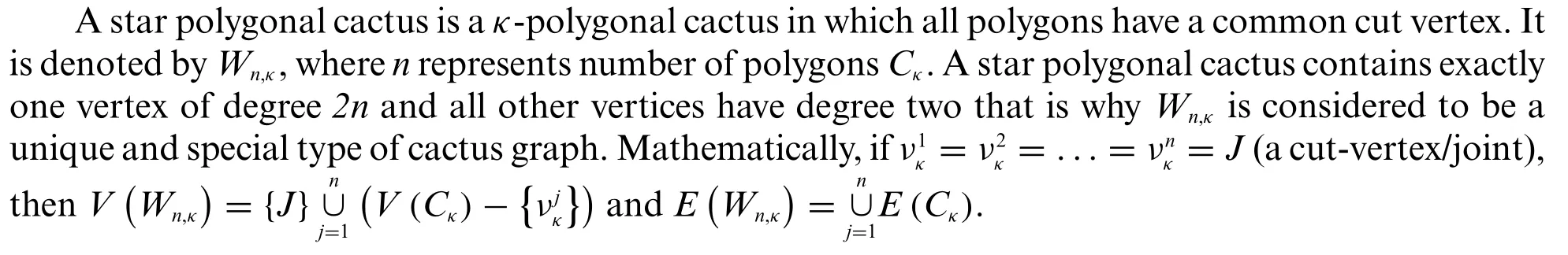
We have the following results on metric dimension problem regarding star cactus.

Lemma 2.9.Forκ≥3 andn≥3,ifSis a minimum metric generator forWn,κ,thenSmust contain at least one vertex from each block.

Proof.Suppose contrarily thatSdoes not contain a vertex fromjthblockBj(say), then we have verticesyandxinBj,wherexandyare neighbors of the jointJ,andd(x,u)=d(u,J)+1,d(y,u)=d(u,J)+1 for allu∈S. ThusmS(x)=mS(y), a contradiction. HenceSmust contain at least one vertex from each block ofWn,κ.

It can be seen that all the metric vectors are distinct, which yields thatSis a metric generator ofWn,κ.

Theorem 2.16.For oddκ≥3 andn≥3,dim(Wn,κ)=n.

Proof.LetSbe a minimum metric generator.Wn,κhasnblocks andSmust contain a vertex from each block,by Lemma 2.9.So,dim(Wn,κ)= |S| ≥n.Moreover,Lemma 2.10 provides a metric generator forWn,κof cardinalityn,which yields thatdim(Wn,κ)≤n.

Lemma 2.11.For evenκ≥4 andn≥3, ifSis a minimum metric generator forWn,κ, thenScontains single vertex from only one block.

Proof.Suppose contrarily thatScontain only one vertex from two blocks,vertexxfromjthblockBjand vertexyfromtth blockBt.There are two possibilities to discuss:

andd(w,s)=d(z,s)for eachs∈S-{x,y}. HencemS(w)=mS(z), a contradiction. Therefore,Scontains single vertex from only one block.

From the above Lemma,we have the following consequence:

Corollary 2.1.For evenκ≥4 andn≥3,a minimum metric generatorSforWn,κmust contain at least two vertices from each of(n-1)blocks.

Lemma 2.12.For evenκ≥4 andn≥3,ifSis a minimum metric generator forWn,κ,then|S|≥2n-1.

Proof.There arenblocks inWn,κandSmust contain a vertex from each block, by Lemma 2.9.So,Smust contain one vertex from only one block and at least 2(n-1)vertices from the remaining(n-1)blocks,by Lemma 2.11 and Corollary 2.1.Thus|S|≥1+2(n-1)=2n-1.

Lemma 2.13.For evenκ≥4 andn≥3,the setis a metric generator forWn,κ.

Proof.To prove thatSis a metric generator,we need to show that for each pair(x,y)of vertices inWn,κ,there is generally a vertex inSwhich identifies the pair(x,y).We consider the following cases:

Case-IWhenever both the verticesxandyare in the same blockBtofWn,κ.Then there are two possibility:

1. Ifxandyare not BDS,then there is a vertexs∈Ssuch thatd(x,s)/d(y,s)andmS(x)mS(y).So,sidentifies(x,y).

2. Ifxandyare not BDS, thend(x,νj)d(y,νj). So, there is a vertexs∈S-{such thatd(x,s)=d(x,νj)+d(νj,s),d(x,s)=d(x,νj)+d(νj,s)andd(x,s)/d(y,s).Hence,mS(x)=mS(y).

Case-IIWhenever bothxandydo not belong to the same block.Suppose thatx∈Bjandy∈Bt,wheretj.Then,we have two possibilities:

1. Ifx, yare BDS, then there are two verticesu,νinSeitheru,ν∈Btoru,ν∈Bjsuch thatd(x,u)d(y,u) or d(x,ν)/d(y,ν).So,the pair(x,y)must be identified.

2. Ifx,yare not BDS,then there is a vertexs∈Slying in the block containingxory,such thatd(x,s)d(y,s).So,sidentifies the pair(x,y).

Case-IIIWhenever eitherxoryis a joint vertex, without any ambiguity, we assume thatxis a joint vertex andylies in any blockBj. Ifxandyare adjacent, then there is always a vertexu∈S,whereubelongs to the blockBt,tjsuch thatd(u,x)=d(u,y)- 1 andd(u,y)=d(u,y)+ 1.HencemS(x)mS(y). Otherwise, there is a vertexs∈Ssuch thatd(s,x)=d(s,y)-d(y,x). So,d(s,x)d(s,y).Hencesidentifies the pair(x,y).

All these cases proved thatSperforms metric identification forWn,κ.It completes the proof.

Theorem 2.17.For evenκ≥4 andn≥3,dim(Wn,κ)=2n-1.

Proof.LetSbe a minimum metric generator forWn,κ.By Lemma 2.12,|S|≥2n-1,sodim(Wn,κ)≥2n-1. Moreover,Wn,κhas a metric generator of cardinality 2n-1, by Lemma 2.13, which implies thatdim(Wn,κ)≤2n-1.It completes the proof.

3 Concluding Remarks

A family of graphs has a constant metric dimension ifdim(G)is finite and independent of the order of the graph in the family.Ifdim(G)varies and depends on the order of the graph,then the metric dimension is known as unbounded[9,21].Two types of polygonal cacti are considered in the context of resolvability(metric identification)and computed the exact value of metric dimension.We analyzed that these families of cactus graphs possessed constant metric dimension,only in few cases.Precisely,we investigated that the family of star polygonal cactusWn,κpossessed the unbounded metric dimension,whereas the family of chain polygonal cactus possessed both the constant and unbounded metric dimensions in various cases,described as follows:

• The familyHn,κof chain polygonal cactus possessed the constant metric dimension whenever:

-Hn,κconsisted of more than two polygons of length 3.

- there were only three polygons inHn,κof odd length more than 3.

- there were only four polygons inHn,κof even length more than 2.

- otherwise,Hn,κpossessed the unbounded metric dimension.

• The familyRn,κof chain polygonal cactus possessed the constant metric dimension whenever:

-Rn,κconsisted of two,three and four polygons of length more than 2.

-Rn,κconsisted of more than two polygons of length 5.

-d(vi,vi+1)=inRn,κfor oddκ≥7 and anyn≥3.

- otherwise,Rn,κpossessed the unbounded constant metric dimension.

Funding Statement:The authors received no specific funding for this study.

Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.