On Riemann-Type Weighted Fractional Operators and Solutions to Cauchy Problems

Muhammad Samraiz,Muhammad Umer,Thabet Abdeljawad,Saima Naheed,Gauhar Rahman and Kamal Shah

1Department of Mathematics,University of Sargodha,P.O.Box 40100,Sargodha,40100,Pakistan

2Department of Mathematics and Sciences,Prince Sultan University,P.O.Box 66833,Riyadh,11586,Saudi Arabia

3Department of Medical Research,China Medical University,Taichung,40402,Taiwan

4Department of Mathematics and Statistics,Hazara University Mansehra,Mansehra,21300,Pakistan

5Department of Mathematics,University of Malakand,Chakdara Dir(L),KPK,18000,Pakistan

ABSTRACT In this paper,we establish the new forms of Riemann-type fractional integral and derivative operators.The novel fractional integral operator is proved to be bounded in Lebesgue space and some classical fractional integral and differential operators are obtained as special cases.The properties of new operators like semi-group,inverse and certain others are discussed and its weighted Laplace transform is evaluated.Fractional integro-differential freeelectron laser (FEL) and kinetic equations are established. The solutions to these new equations are obtained by using the modified weighted Laplace transform. The Cauchy problem and a growth model are designed as applications along with graphical representation.Finally,the conclusion section indicates future directions to the readers.

KEYWORDS Weighted fractional operators;weighted laplace transform;integro-differential free-electron laser equation;kinetic differ-integral equation

1 Introduction

The analysis and applications of non-integer order derivatives and integrals are known as fractional calculus. Fractional calculus theory has developed rapidly in recent years and has played a number of pivotal roles in science and engineering, helping as a strong and efficient resource for numerous physical phenomena.Over the last two decades,it has been extensively studied by several mathematicians[1-6].

The literature suggests that the Riemann-Liouville fractional(RLF)derivative plays a crucial part in fractional calculus.Researchers are encouraged to broaden the meanings of fractional derivatives due to the variety of applications. Some of the applications are available in [7-12]. Akgül [13] and Atangana et al.[14]investigated the fractional derivative with non-local and non-singular kernel.In[15]Caputo et al.examined the non-local fractional derivative which can work more efficiently with Fourier transformation.Some applications of fractional order operators are available in[16,17].The existence of solution of Riemann-Liouville fractional integro-differential equations with fractional non-local multi-point boundary conditions and system of Riemann-Liouville fractional boundary value problems withρ-Laplacian operators are briefly discussed in[18,19].Currently,Jarad et al.[20]defined the weighted fractional derivatives and fractional integrals.To study fractional calculus and its applications,we refer to the readers[21-27].

Motivated by the recent studies presented in[20]and by combining this idea to extend the RLF operators,we will introduce the generalized weighted(k,s)-RLF operators and study their properties.The weighted Laplace transform to such fractional operators and some applications in mathematical physics will be discussed.Finally,we will finish with some closing remarks.

In the beginning,we recall some related definitions and notions.The integral form of thek-gamma andk-beta functions given in[28]are defined as follows:

Definition 1.1.Thek-gamma function is defined by

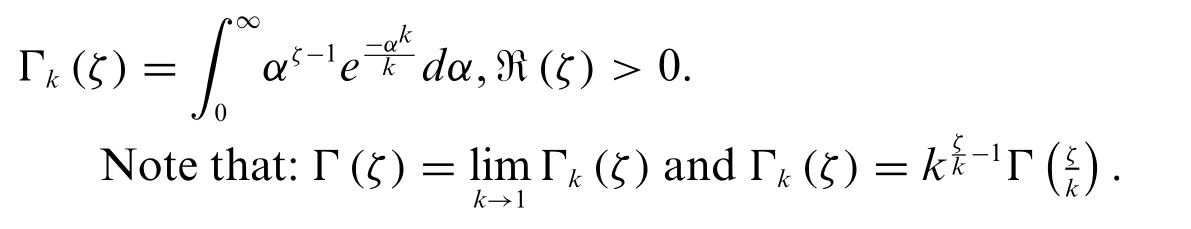
Definition 1.2.For ℜ(ζ),ℜ(η)＞0 andk ＞0,thek-beta function is defined as

Definition 1.3.[29]Suppose that the Ω be a continuous function on interval[a,b].Then weighted(k,s)-RLF integral of orderζis given by

whereζ,k ＞0,ρ(α)0 ands∈R{-1}.

Definition 1.4.[29]Let Ω be a continuous function on[0,∞)ands∈R{-1},withn=[ζ]+1,ζ,ρ(α)0,andk ＞0.Then for all 0＜t ＜α ＜∞

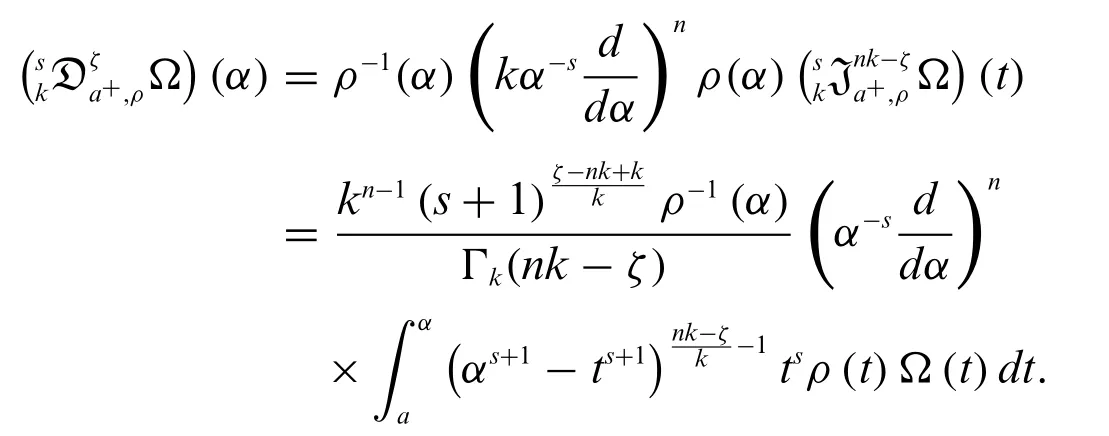
whereis a weighted(k,s)-RLF integral.

Jarad et al.[20]defined the generalized weighted Laplace transform as follows:

Definition 1.5.Letρ, Υ be functions with values in R. Furthermore, Υ(α)is continuous and Υ＇(α)＞0 on[a,∞).The weighted generalized Laplace transform of Ω is given by

and is true for all values ofufor which(1)exists.

Theorem 1.1.[20]If Ω ∈ACρ[a,α)and of weightedΥ-exponential order.Suppose that the DρΩ be a piecewise continuous function on every interval [a, T], then the weighted generalized Laplace transform of DρΩ exists and

The generalized form of Theorem 1.1 is stated in the next result.

Definition 1.6.[20]The generalization of the weighted convolution of Ω and Υ is defined by

2 Generalized Weighted(k,s)-Riemann-Liouville Fractional Operators

In this section,we introduce the generalized weighted(k,s)-RLF operators and describe some of their features.

Definition 2.1.Suppose that the Ω be a continuous function on the finite real interval[a,b]and Υ is strictly increasing function.Then the generalized weighted(k,s)-RLF integral of orderζis defined by

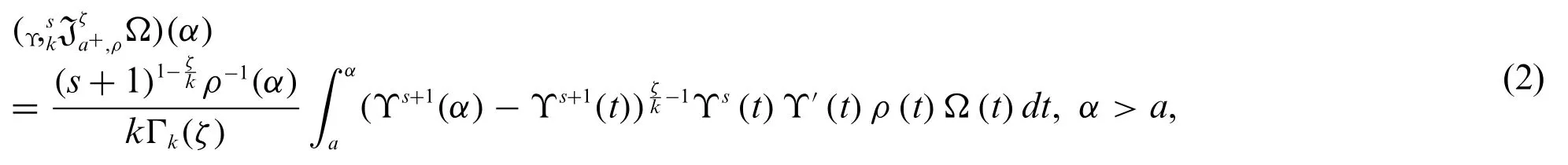
whereζ,k ＞0,ρ(α)0,s∈R{-1}andΥs+1(x)=(Υ(x))s+1.

The integral operator defined in 2 cover many fractional integral operators.For instance,

I. if we sets=0 andk=1 in(2),we get the generalized weighted-RLF integral given in[20].

II. If we setΥ(α)=αin(2),we get the weighted(k,s)-RLF integral presented in[29].

III. If we setρ(α)=1 andΥ(α)=αin(2),we get the weighted(k,s)-RLF integral[29].

IV. If we sets=0,Υ(α)=αandρ(α)=1 in(2),k-RLF integral is obtained[30].

V. If we setk=1,s=0,Υ(α)=αandρ(α)=1 in(2),it gives RLF integral[3].

VI. Fors→-1+,Υ(α)=αandρ(α)=1 in(2),we obtaink-Hadamard fractional integral[31].

The corresponding weighted generalized fractional derivative is defined by the following definition.

Definition 2.2.Let Ω be continuous function on[0,∞)ands∈R{-1},n=[ζ]+1,ζ,k ＞0,andρ(α)0.Then for all 0＜t ＜α ＜∞,the inverse derivative operator of integral operator 2 is defined by

whereis a generalized weighted(k,s)-RLF integral.

There are many other fractional derivative operators as special cases of the operator(3).

I. If we chooses= 0 andk= 1 in(3),we get the weighted(k,s)-RLF derivative presented in[20]

II. If we chooseΥ(α)=αin(3),we get weighted(k,s)-RLF derivative presented in[29].

III. If we chooseρ(α)=1 andΥ(α)=αin(3),we get(k,s)-RLF derivative[32].

IV. If we sets=0,Υ(α)=αandρ(α)=1 in(3)it gives tok-RLF derivatives[33].

V. If we setk=1,s=0,Υ(α)=αandρ(α)=1 in(3),it reduces to RLF derivative[34].

VI. (3)reduces to k-Hadamard fractional derivative fors→-1+,Υ(α)=αandρ(α)=1[31].

In the following definition,we define the space where the generalized weighted(k,s)-RLF integral is bounded.

Definition 2.3.Letfbe defined on [a,b] and,b), 1 ≤p≤∞be the space of all Lebesgue measurable functions for which∞,where

Proof.For 1 ≤p ＜∞,we have

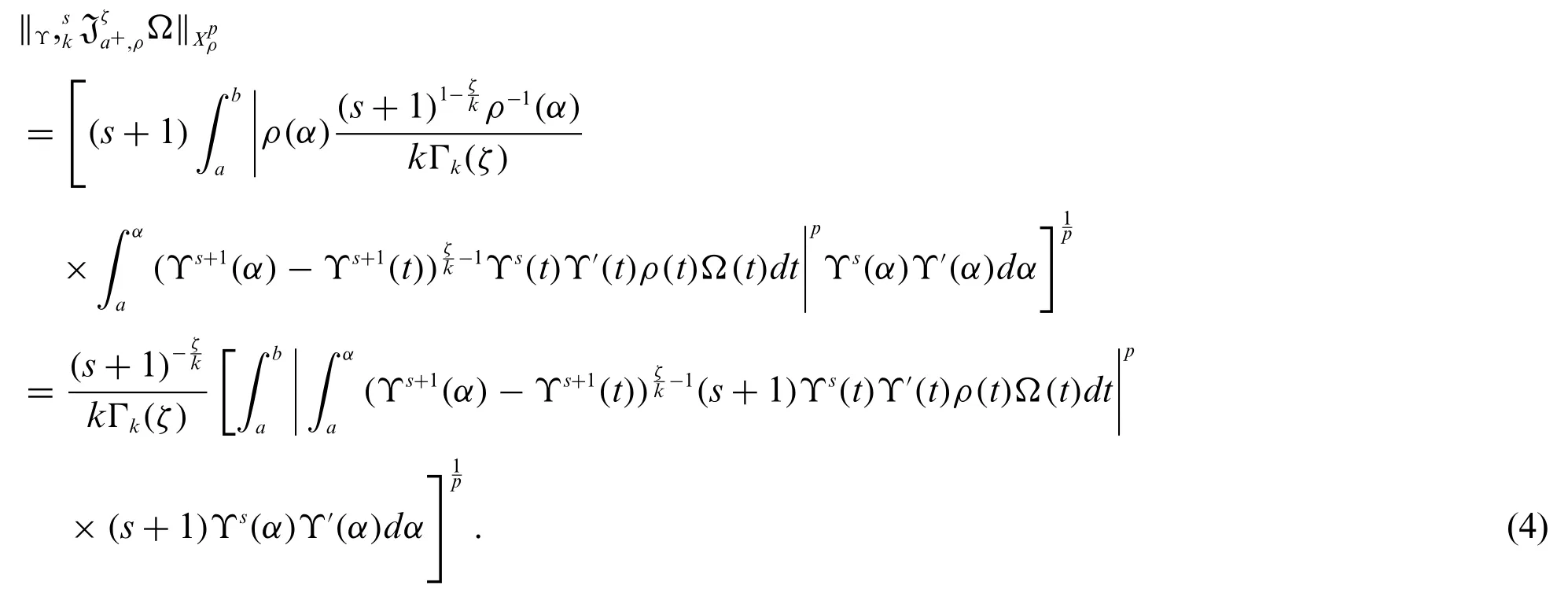
SubstitutingΥs+1(α)=vandΥs+1(t)=uon the right side of(4),we obtain

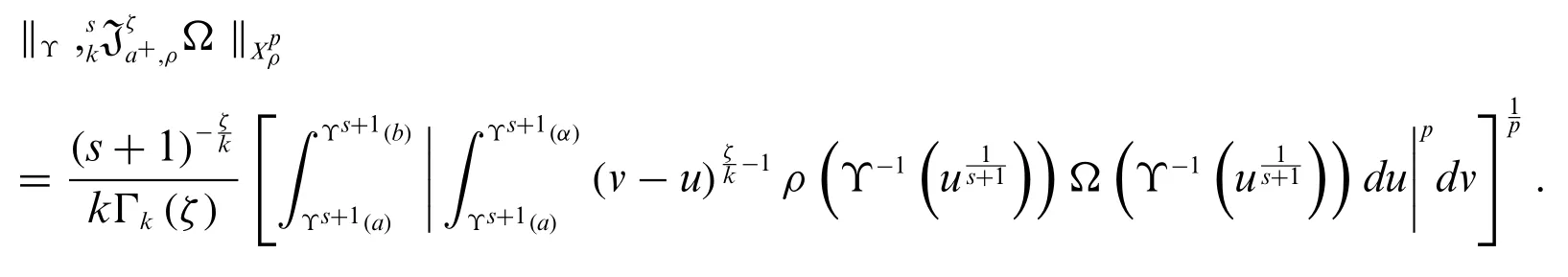
By using Minkowski’s inequality,we have

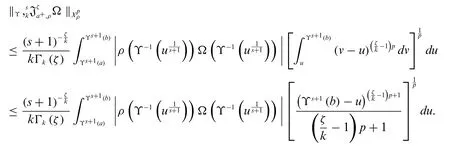
Applying Hölder’s inequality,we get

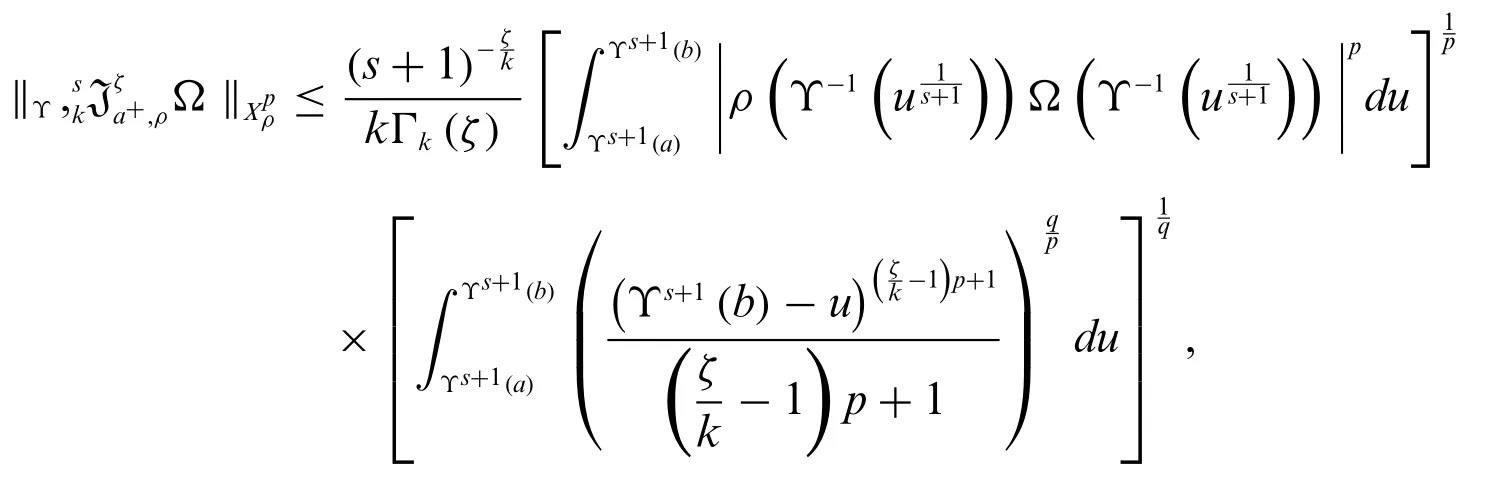
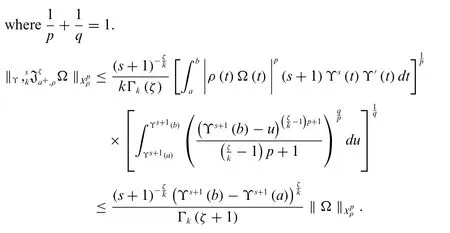
Forp=∞,we obtain

Hence the proof is done.

Theorem 2.2.Let Ω be continuous on[0,∞)ands∈R{-1}andρ(α)0,n=[ζ]+1.Then for all 0＜a ＜α.

whereζ,k ＞0 andnk-ζ ＞0.

Proof.Consider

which gives

This proved the inverse property.

Corollary 2.1.Let the function Ω be continuous on[0,∞)ands∈R{-1}andρ(α)0,m=[η]+1,n=[ζ]+1.Then for all 0＜a ＜α

whereζ,η,k ＞0.

Corollary 2.2.Let the function Ω be continuous on[0,∞)ands∈R{-1},ρ(α)0,n=[ζ]+1,m=[η]+1 andζ+η ＜nk.Then for all 0＜a ＜α

whereζ,η,k ＞0.

Proof.By using Definition 2.2,we have

By using Theorem 2.2,we have

which implies

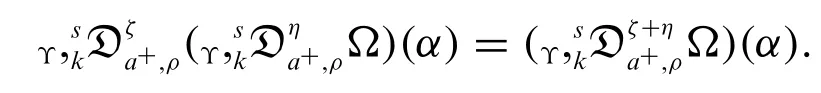
Hence the semi-group property of new derivative operator is proved.

Corollary 2.3.Suppose that the Ω be a continuous function on [0,∞)andζ,η∈R+,ρ(α)0 ands∈R{-1}.Then for all 0＜a ＜α

wheren=[ζ]+1,m=[η]+1 andζ+η ＜nk.

Theorem 2.3.Let the function Ω be continuous on[a,b]andk ＞0,ρ(α)0 ands∈R{-1}

for allζ,η ＞0 andα∈[a,b].

Proof.By utilizing the Definition 2.1 and Dirichlet’s formula,we get

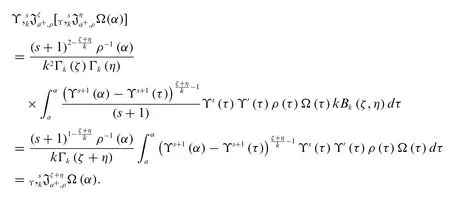
This completes the proof.

Theorem 2.4.Letζ,η,k ＞0,ρ(α)0 ands∈R{-1}.Then we have

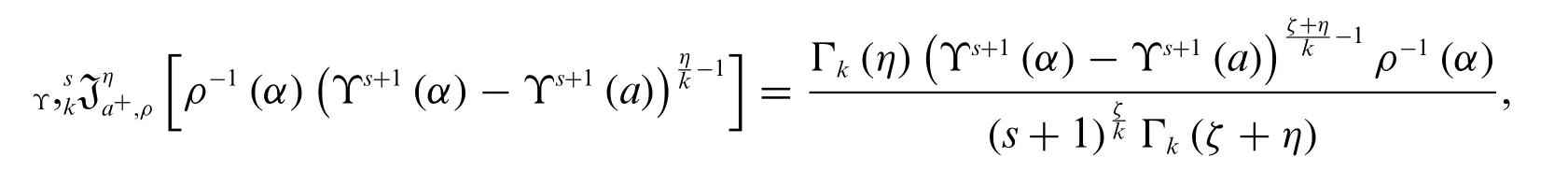
where Γk(.)represents thek-Gamma function.

Proof.By Definition 2.1,we get

The proof is done.

Example 2.1.Corresponding to the choice of the parameterss= 0,k= 1,η= 3,a= 0 andρ(t)=1,we get the following graphs with different choices of the function Υ(t).

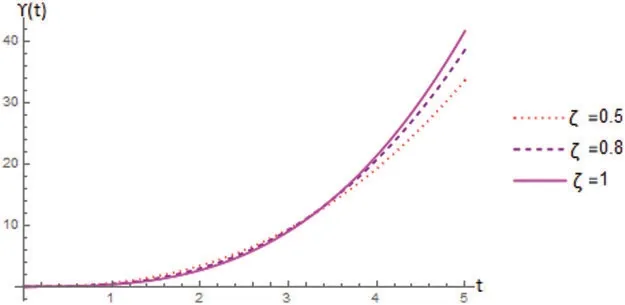
Figure 1:For Υ(t)=t the graph in Fig.1 shows the increasing behaviour with 0 +≤t ≤5

3 The Generalized Weighted Laplace Transform

In the following section, we use the weighted Laplace transformation to the new fractional operators.Firstly,we present the following definition which is a modified form of the Definition 1.5.

Definition 3.1.Suppose that the Ω be a real valued function defined on Ω ∈[a,∞)ands∈R{-1}.The weighted generalized Laplace transform of Ω is given by

holds for all values ofu.

Proposition 3.1.

Proof.By the Definition 3.1,we have

Substitutet=(Υs+1(α)-Υs+1(a))on the right side of(8),we get

the proof is done.

Theorem 3.1.Let the function Ω be continuous on each intervala,αand of weighted Υs+1-exponential order.Then

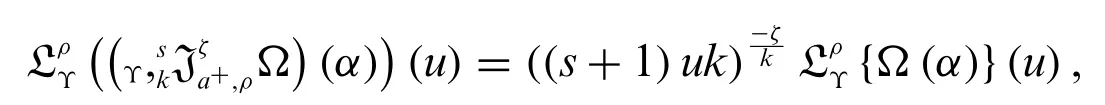
wherek ＞0,ρ(α)0,s∈R{-1}.

Proof.By the Definitions 2.1,1.6 and Proposition 3.1,we have

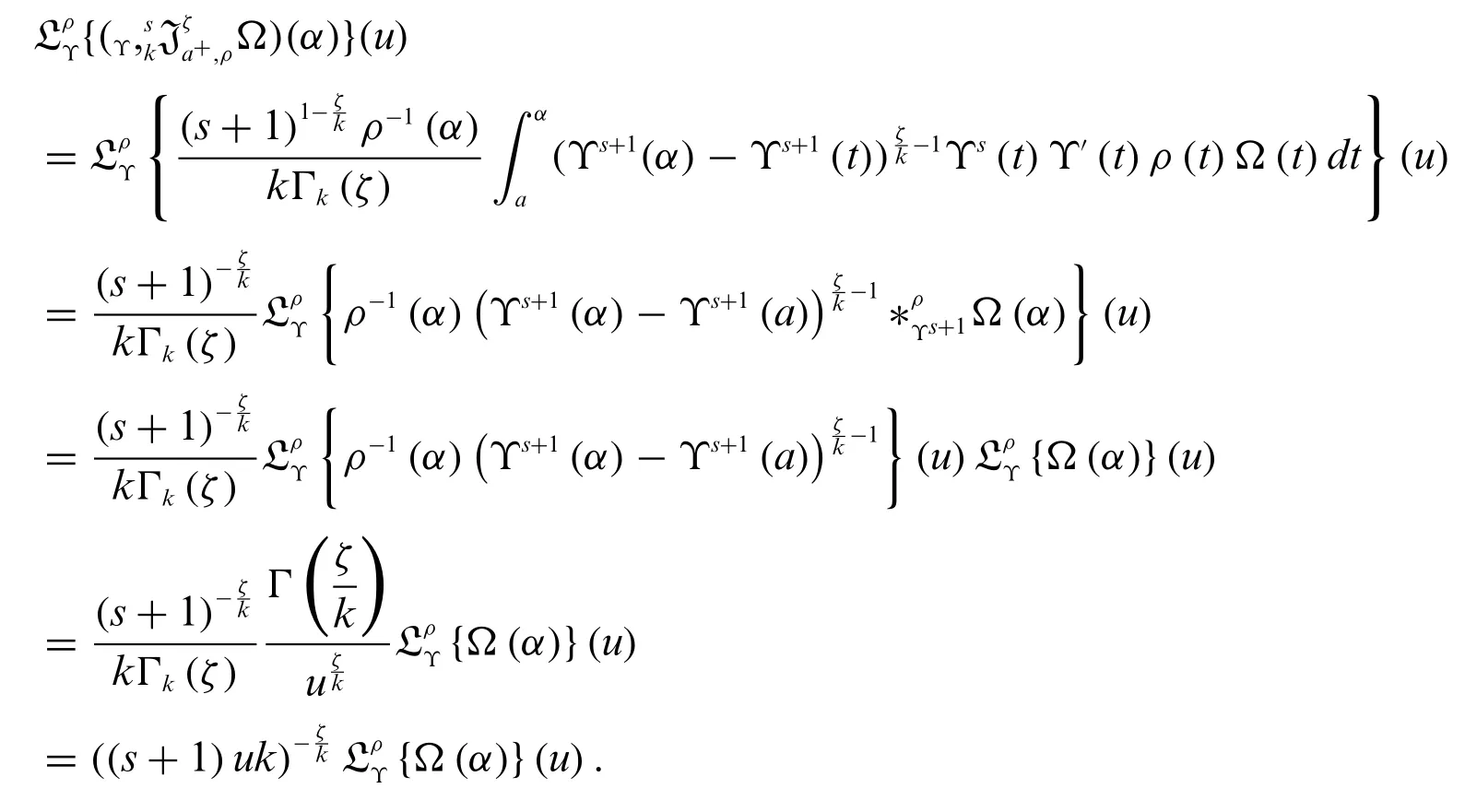
This completes the proof.

Theorem 3.2.The generalized weighted Laplace transform of the novel derivative is

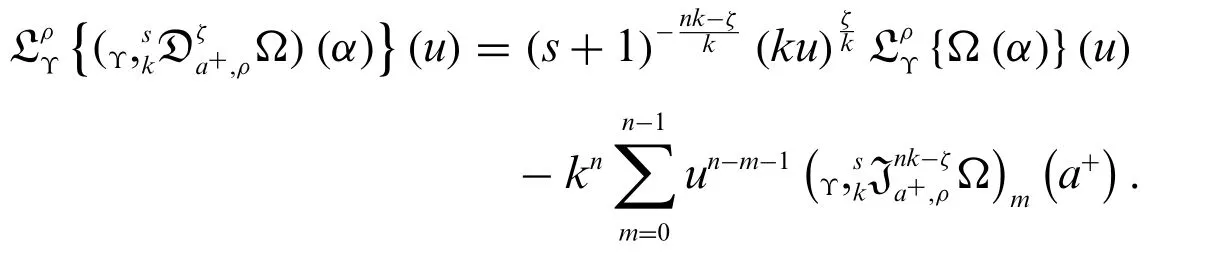
Proof.By the Definition 2.2,Theorem 1.2 and Theorem 3.1,we get

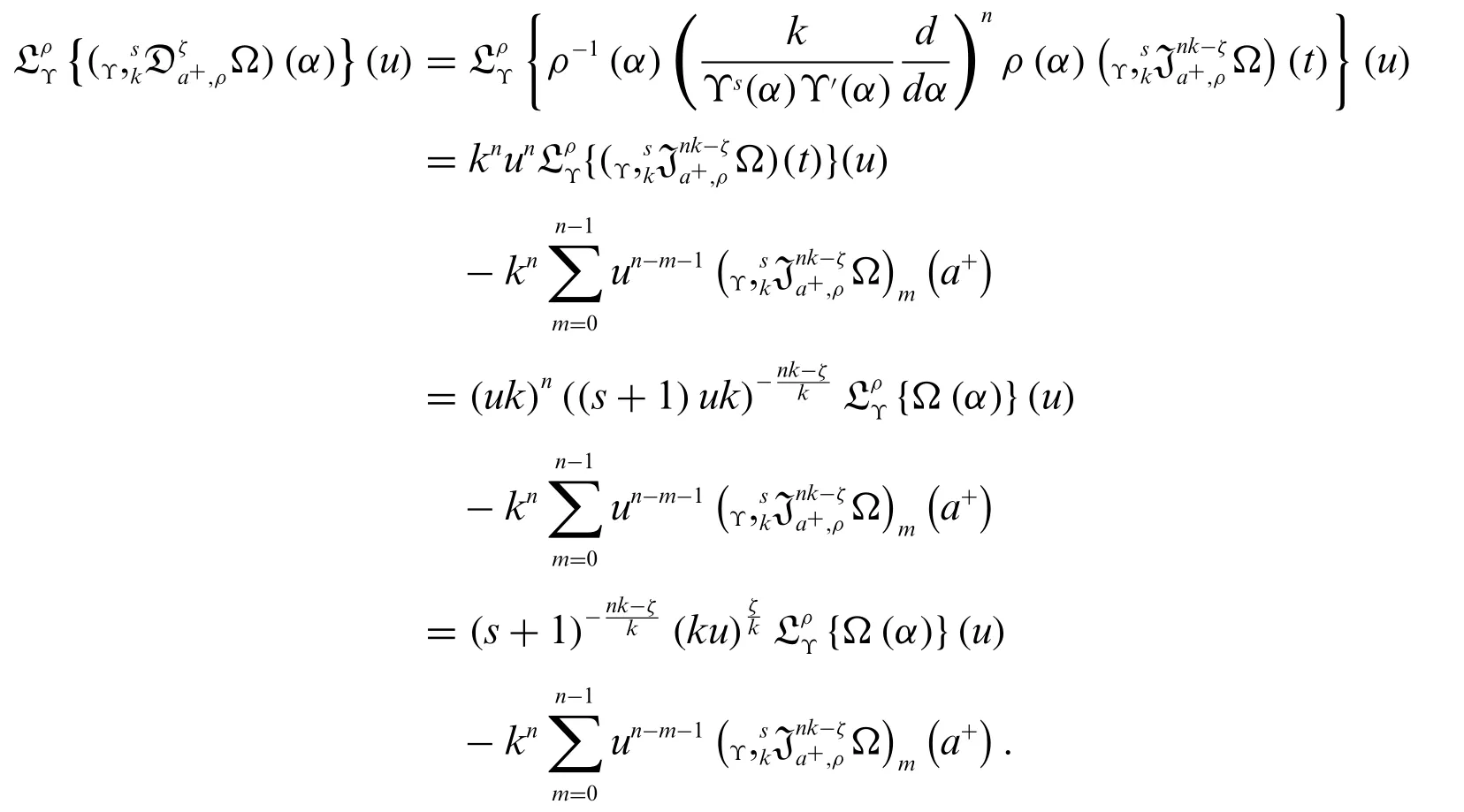
The proof is completed.

4 Fractional Free Electron Laser Equation with Solution

In this section,we investigate the fractional generalization FEL by using the introduced fractional integral given in(2)and the fractional derivative presented in(3).The series form solution is obtained by employing the weighted generalized Laplace transform introduced by Jarad et al. [20].

Theorem 4.1.The solution of the cauchy problem

whereα∈(0,∞),f∈L1[a,∞),a≥0,ρ0andλ∈R is given by

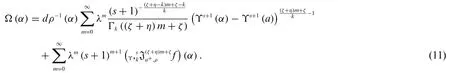
Proof.Applying generalized weighted Laplace transform on(9)and using Theorems 3.1 and 3.2,we get

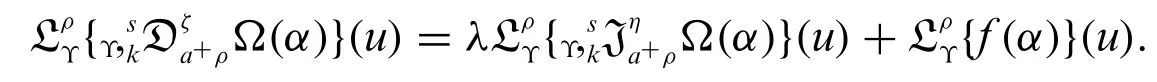
The above equation implies that

By using the inverse Laplace transform,we obtain

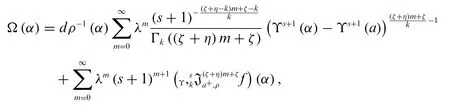
the result is completed.

Remark 4.1.If we sets= 0,k= 1,ζ=η= 1,f(α)= 0,ρ=ir,λ= -iΠp,(r,p∈R)and Υs+1(α)=α,in 9 and 10,then the original free electron laser equation given in[35]is obtained.

The following is the cauchy problem based on Theorem 4.1.

Example 4.1.The solution of the cauchy problem

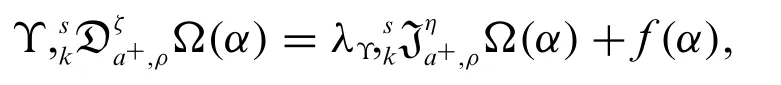
where

subject to the condition

withα∈(0,∞),a≥0,ρ0 andλ∈R is given by

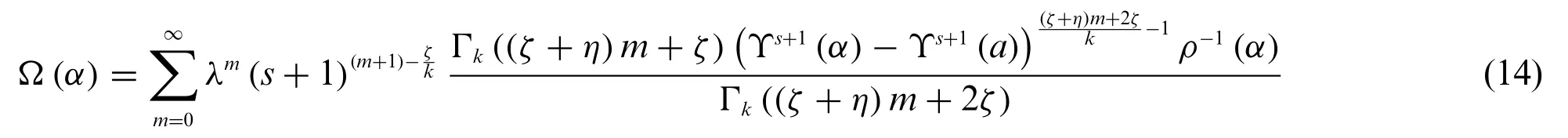
Solution 4.1.For the function given by(12)subjected to the condition presented in(13)the Eq.(11)becomes

Consider

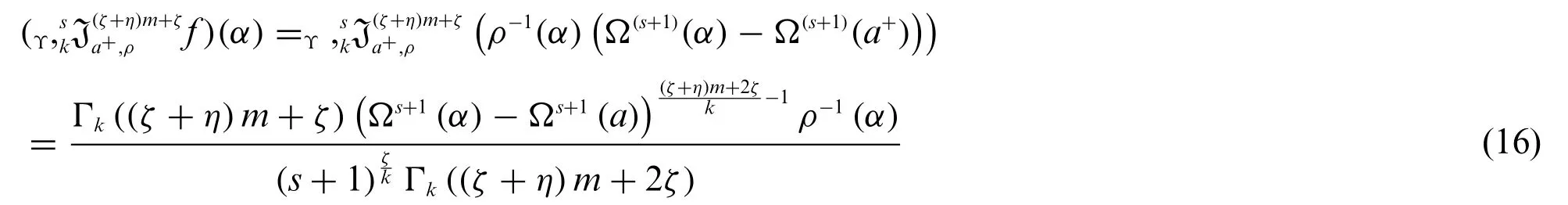
Using(16)in(15),we obtain(14).

5 Fractional Kinetic Differ-Integral Equation with Solution

In the last decade, fractional calculus has opened up new vistas of research and brought a revolution in the study of fractional PDE’s and ODE’s[36-38].Fractional kinetic equation has been successfully used to predict physical phenomena such as diffusion in permeable media, reactions and unwinding forms in complicated framework. The fractional form of the kinetic equation has gained attention due to the its relationship with the CTRW-theory [39]. This section is dedicated to investigating a new weighted fractional kinetic equations to explain the continuity of the motion of the material and the fundamental equations of natural sciences.The series solution of this new fractional kinetic equation by applying weighted generalized fractional laplace is also part of this section.The fractional kinetic equation is

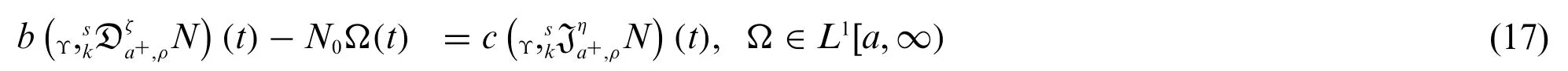
subject to

wherea,ζ≥0,b,c∈R(b0),k ＞0,n=

Theorem 5.1.The solution of(17)with initial condition(18)is

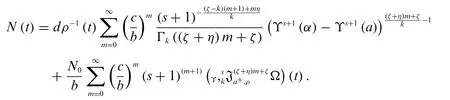
Proof.By applying the modified weighted Laplace transform on both side of(17),we get

Using Theorems 3.1 and 3.2,we get

By applying the inverse Laplace transform,we get

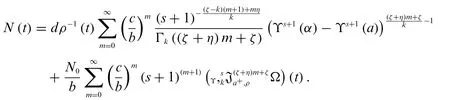
Next,we include an example in the field of engineering using our defined operators.

Example 5.1.Consider a famous growth model given by

subject to the condition

whereThe solution to the growth model(19)is

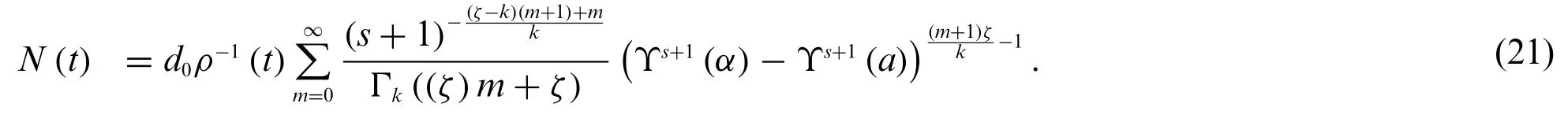
Solution 5.1.By choosingb=c= 1N0= 0,η= 0 in(17)anda= 0,d=d0in(18),we obtain the growth model with solution (21). Further with the choice of parametersk= 1,s= 0,ζ= 1.5,d0=1,ρ(t)=1 and Υ(α)=α,we get

The graph of the functionN(α)is presented as follows:

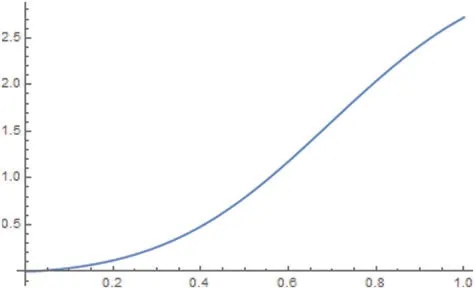
Figure 2:For 0 ＜α ＜1,the graph in Fig.2 indicates the increasing and convergent behaviour of the infinite series

6 Conclusion

In this paper,the weighted generalized fractional integral and derivative operators of Riemanntype are investigated. We discuss some properties of the fractional operators in certain spaces.Specifically, the semi-group and inverse properties are proved for the introduced operators. The modified weighted Laplace transform of novel operators is also examined which is compatible with the introduced operators.It is worth mentioning that many established operators unify some operators that exist in literature. Finally, the solutions of the weighted generalized fractional free electron laser and kinetic equations are obtained by utilizing the skillful technique of the weighted Laplace transform, which has been applied in many mathematical and physical problems. Furthermore, a Cauchy problem and a growth model for a specific choice of parameters involved are designed and sketched in their graphs to check the validity.

Acknowledgement:The authors T. Abdeljawad and K. Shah would like to thank Prince Sultan University for supporting through TAS research lab.

Funding Statement:The authors are thankful to Prince Sultan University for paying the article processing charges.

Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.