考虑温度影响的机器人关节摩擦模型

张一楠 丁建完

华中科技大学国家CAD支撑软件工程技术研究中心，武汉，430074

0 引言

串联机器人的建模仿真与基于模型的控制需要精确的机器人动力学模型，而关节摩擦模型是机器人动力学模型的重要组成部分。常用的机器人关节摩擦模型为库仑黏滞摩擦模型，除此之外，还有Stribeck模型[1]、Dahl模型[2]、Maxwell-slip模型[3]、LuGre模型[4]等。机器人实际运行中，关节摩擦会受温度变化的影响[5]，因此有必要对其进行探究。

ANDRE等[6]通过实验探究了温度对机器人关节摩擦力矩的影响。GAO等[7]建立并验证了考虑温度的协作机器人非线性摩擦模型。YAN等[8]通过带温度影响的静态关节摩擦模型研究了机械臂的控制方法。吴晓敏等[9]在Stribeck模型的基础上提出了考虑温度影响的摩擦力矩模型。LORINC等[10]通过对环境温度和外壳温度的测量来估计关节内部温度。上述研究考虑了温度对机器人关节摩擦力矩的影响，提出了相应模型，但依赖对温度的直接测量或间接估计，而在大部分实际应用场景中，安装传感器、测量机器人关节温度是不现实的。

为了避免对温度的测量或估计，PAGANI等[11]提出了基于热平衡的关节发热微分模型，在无需温度传感器的前提下预测机器人工作周期中的摩擦力矩变化。CARLSON等[12]将摩擦力矩视作以摩擦损耗为输入的系统，避免了温度测量，并对所提出的方法进行了实验评估。对于连续运行状态下的机器人，SIMONI等[13]通过探究不同运行时间下关节摩擦的变化，研究温度对关节摩擦的影响，并提出了连续运转下的关节摩擦模型。PAGANI等[14]考虑了关节结构特点，对关节传热模型进行改进，更准确地描述传热现象。

上述研究中的研究对象大多为以润滑油为润滑介质的工业机器人，且均假设关节热源为单一的机械摩擦。但在实际情况下，伺服电机、伺服驱动等组件产生的热量同样对关节的升温有贡献，并且不同关节结构和润滑介质的机器人的摩擦力矩也不尽相同。

1 机器人关节摩擦

1.1 关节摩擦主要来源

机械摩擦是一种复杂的物理现象，目前很难通过数值计算对实际摩擦做出精确估计[15]。机器人关节摩擦来源众多、成因复杂。对协作型串联机器人关节而言，除伺服电机、传感器、伺服驱动外，还包含减速器与滚动轴承等组件。

本文研究的协作机器人关节安装了谐波减速器，并采用润滑脂作为润滑介质。关节内部机械摩擦的主要来源为滚动轴承摩擦与减速器轮齿啮合摩擦[7]。

1.1.1滚动轴承摩擦

滚动轴承的摩擦成因较为复杂，除轴承的结构、尺寸和外界载荷外，润滑介质的性能对摩擦也有较大的影响[16]。滚动轴承的摩擦主要包括载荷摩擦、润滑介质带来的黏性摩擦、轴承滚子的自旋摩擦[17]等。从实际应用出发，可通过经验公式近似计算摩擦力矩[18]：

(1)

式中，M为滚动轴承的摩擦力矩，N/mm；f1为载荷系数；F1为轴承径向载荷，N；dm为轴承平均直径，mm；f0为考虑结构与润滑的系数；ν为润滑介质运动学黏度，m2/s；n为轴承转速，r/min。

1.1.2轮齿啮合摩擦

齿轮的啮合摩擦包含滑动摩擦与滚动摩擦。对于滑动摩擦而言，轮齿只有在完全理想情况下才处于完全弹流润滑状态，该状态下的啮合摩擦可通过Dowson线接触润滑理论[19]来描述。实际的啮合摩擦常处于部分弹性流体润滑的状态，其啮合平均摩擦因数为[20]

(2)

式中，Fn为齿面法向载荷，N；b为有效齿宽，mm；ρ为润滑介质动力学黏度，Pa·s；vHm、vTm分别为平均滑动速度和平均滚动速度，m/s。

对于轮齿啮合的滚动摩擦，可采用经验公式对摩擦损耗进行近似估计[21]：

(3)

式中，PR为齿面滚动摩擦损失功率，kW；h为弹性动力油膜厚度，mm；ζ为压黏系数，MPa-1；R为综合曲率半径，mm；E为综合弹性模量，MPa；ψ为载荷系数，N/mm。

由式(2)、式(3)可直观得出，润滑介质的黏度对啮合摩擦的影响较为复杂。

实际的机器人关节除了上述的轴承摩擦和齿轮啮合摩擦，还存在搅动摩擦、减速器弹性形变等效摩擦等摩擦，并且不同摩擦的具体占比很难通过计算得到。因此，对于机器人关节整体而言，很难通过数值计算的方式得到完全准确的摩擦力矩。从机器人的应用层面考虑，可以将关节简化为整体，通过数学模型来研究关节整体的摩擦力矩。

1.2 整体关节摩擦模型

在机器人应用层面上，目前广泛采用的关节摩擦模型主要有库仑黏滞摩擦模型、Stribeck摩擦模型、LuGre摩擦模型[22]。

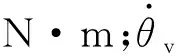
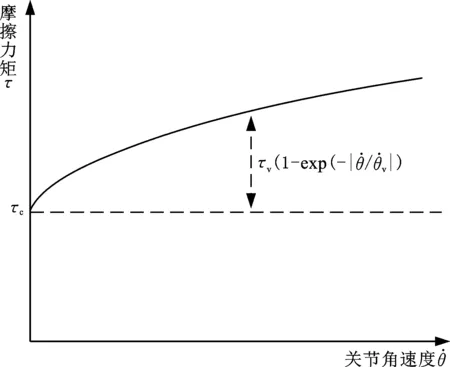
图1 关节非线性摩擦模型Fig.1 Nonlinear friction model of joint

图1所示摩擦模型的摩擦力矩为

(4)

由式(4)可知，该模型没有考虑关节摩擦的Stribeck现象。润滑脂一般为非牛顿流体，其剪切应力与剪切速率为非线性关系[23]，因此机器人关节摩擦力矩大小随关节转速的提高非线性增长。

在机器人的实际应用中，尽管关节转速并非恒定，但关节转速一般高于出现Stribeck现象的临界转速，并且采用脂润滑的协作机器人的Stribeck现象相对不明显，因此本文采用图1所示的数学模型描述关节整体摩擦。

值得注意的是，实际工作的机器人关节存在加减速，此时的摩擦力矩可能存在迟滞现象，但实际的关节速度变化往往不大，摩擦力迟滞现象不明显，因此为便于研究，本文忽略摩擦力矩的迟滞现象。

1.3 温度对摩擦的影响

相关研究表明，温度主要通过影响润滑介质的动力学黏度来间接影响摩擦力矩。润滑介质的动力学黏度可表示为温度的指数函数[24]，随温度的升高而非线性降低。由1.1节分析可知，无论是滚动轴承摩擦还是轮齿啮合摩擦，其摩擦力矩都会受润滑脂黏度的影响，并且与黏度呈非线性相关。

文献[8-9，13]采用扩展Stribeck模型描述温度对工业机器人关节摩擦的影响。工业机器人关节采用润滑油为润滑介质，随着关节温度的升高，黏滞摩擦减小，但库仑摩擦和混合润滑阶段的摩擦反而会增大。

研究发现，脂润滑机器人的库仑摩擦力矩τc基本不受温度变化影响，而黏滞摩擦随温度的升高非线性减小[7]。基于式(4)所述模型，提出了考虑温度影响的扩展模型：

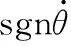
(5)

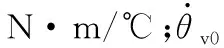
由式(4)、式(5)可知，温度升高时，同一关节转速下的摩擦力矩会非线性减小，但15～40 ℃内的摩擦-温度曲线斜率变化较小[7]。因此，对于温升不大的情况，为简化模型，可将该温度范围内的摩擦力矩与关节温度近似为线性关系：

(6)

式中，T0为初始关节温度，℃；α为摩擦力矩随温度变化的斜率，N·m/℃。

2 连续运转下的关节摩擦模型

机器人在部分应用场景中会有一段时间的持续运行，如打磨、喷涂、焊接等任务中的机器人会按预定的程序重复动作。持续转动的过程中，机器人关节的电机自身产热和关节摩擦产热等因素会使关节不断升温。当关节温度大于外界环境温度时，热量会由关节向外界环境传导。基于上述分析，文献[11-12]提出了连续工作条件下的机器人关节温度变化模型：

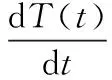
(7)

式中，t为运行时间；T(t)为关节温度；Ts为环境温度，即关节初始温度；ks为描述关节与外界环境传热能力系数；τf(t)ω(t)为当前时刻关节摩擦力矩的产热功率。

由式(6)可知，关节的摩擦力矩会随温度的升高而减小。当温升为ΔT(t)时，式(7)可表示为

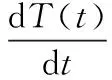
(8)

式中，τfs(t)为不考虑温度影响即环境温度Ts下的关节摩擦力矩。

当关节以固定轨迹连续运行时，由于轨迹周期tc往往远小于机器人连续运行的时间th，因此可将各段的轨迹周期视作th中的一个短暂时刻，tc内各时刻的摩擦功率可近似为其平均功率[20，25]：

(9)

轨迹周期tc内的温度变化很小，因此可忽略tc中的关节温度变化。

综合式(8)、式(9)，可得

(10)

(11)

对式(11)进行拉氏变换可得

(12)

关节温度升高时，各段轨迹周期内的平均黏滞摩擦力矩

(13)

(14)

对式(12)、式(13)进行拉式逆变换，得到关节温度变化量和平均摩擦力矩变化量的时域表示形式：

(15)

式(15)描述了环境温度相对稳定的条件下，机器人在一段连续时间内按照固定轨迹重复运动时关节摩擦力矩的变化，即连续重复工作条件下的机器人关节摩擦力矩模型。对式(15)中的参数进行整理，可得

(16)

理论模型(式(16))仅考虑了关节机械摩擦产生的热量。实际应用中，机械摩擦不是关节产热的唯一因素，因此需要对关节的其他热源进行分析，探究不同热源对关节升温的影响。

机器人电机等组件的产热成因复杂，具体数值的计算难度较大，也超出了本文的研究范围，且受限于实验条件，对发热量进行直接测量也不现实，因此，本文基于前人的研究，对连续运转下的关节热源进行近似估计。

关节运行时，伺服电机存在损耗，且大部分最终转化为热量。电机损耗主要包括铁耗、铜耗、涡流损耗、杂散损耗、机械损耗等。除铜耗外，铁耗、涡流损耗和杂散损耗等受电机电流变化影响较小，机器人按照给定轨迹连续运行时，其电机平均速度基本不变，上述损耗基本恒定。

电机铜耗与导体电阻和电机电流有关。永磁直流电机的铜耗为

(17)

式中，Im为电机绕组电流；Rm为导体电阻。

机器人带载工作时，其铜耗约占总损耗的50%[26]，摩擦力矩约占总力矩的20%[27]。假设摩擦力矩减小30%，总力矩减小6%，此时的电机绕组电流则降为先前的94%。由式(17)可知，此时电机铜耗减小约12%，总损耗减小约6%。

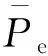
(18)

此时，关节温度与摩擦力矩的时域变化形式为

(19)

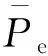
对于连续工作的机器人关节而言，可通过式(19)估计关节摩擦力矩随运行时间的变化，从而避免对关节温度的直接测量。

3 模型验证实验

3.1 实验方案设计

为验证摩擦力矩模型的正确性，需测量连续工作的机器人关节摩擦力矩。机器人关节的输出力矩包括摩擦力矩和驱动关节运动力矩[13]。单个机器人关节的输出力矩为

Jβ=τm-τf+τg

(20)

式中，J为关节折算转动惯量；β为关节角加速度；τm为关节实际输出力矩；τf为关节摩擦力矩；τg为关节需要克服的连杆重力矩。

关节的角加速度β与重力矩τg为0时，关节实际输出力矩τm即为摩擦力矩τf。为准确地测量关节运动时的摩擦力矩，可使机器人关节的轴向与重力方向相同，使式(20)中的τg=0，以消除重力矩的影响。与此同时，驱动关节1做匀速运动，使式(20)中的β=0，以消除关节加速度的影响。

实验所用的机器人是中科深谷六轴串联机器人，如图2所示，其关节1的轴向与重力方向相同，因此本文选取关节1为研究对象做匀速运动，消除重力矩和关节加速度的影响。

图2 六轴串联机器人Fig.2 Six-axis serial robot

为探究不同轨迹下的升温对摩擦力矩的影响，采用多组不同的轨迹即驱动关节1按照不同的速度连续匀速运行，研究不同轨迹对应摩擦模型效果的异同。高速状态下的关节启停会有较大的冲击，因此选取角速度分别为0.4，0.6，0.8，1.0，1.2，1.4，1.6，1.8，2.0，4.0，6.0，8.0，10.0，20.0，30.0°/s(共15组)进行实验。

3.2 数据采集与处理

驱动关节1按照上述角速度连续运行，采集对应的关节输出力矩，通过温度传感器测量关节1外壳处的温度，采集间隔为5 min。关节力矩通过电机电流间接得到，关节输出力矩与电机电流的关系为

τm=ηkmIm

(21)

式中，η为关节减速器减速比；km为伺服电机的转矩常数，N·m/A。

图3所示为关节角速度2.0°/s时的关节力矩和关节角度。通过MATLAB中的巴特沃斯滤波器对采集得到的摩擦力矩进行低通滤波，减小高频噪声的影响。低通滤波关节往复运动时的两段力矩信号后，将其平均值作为该角速度对应的关节摩擦力矩。

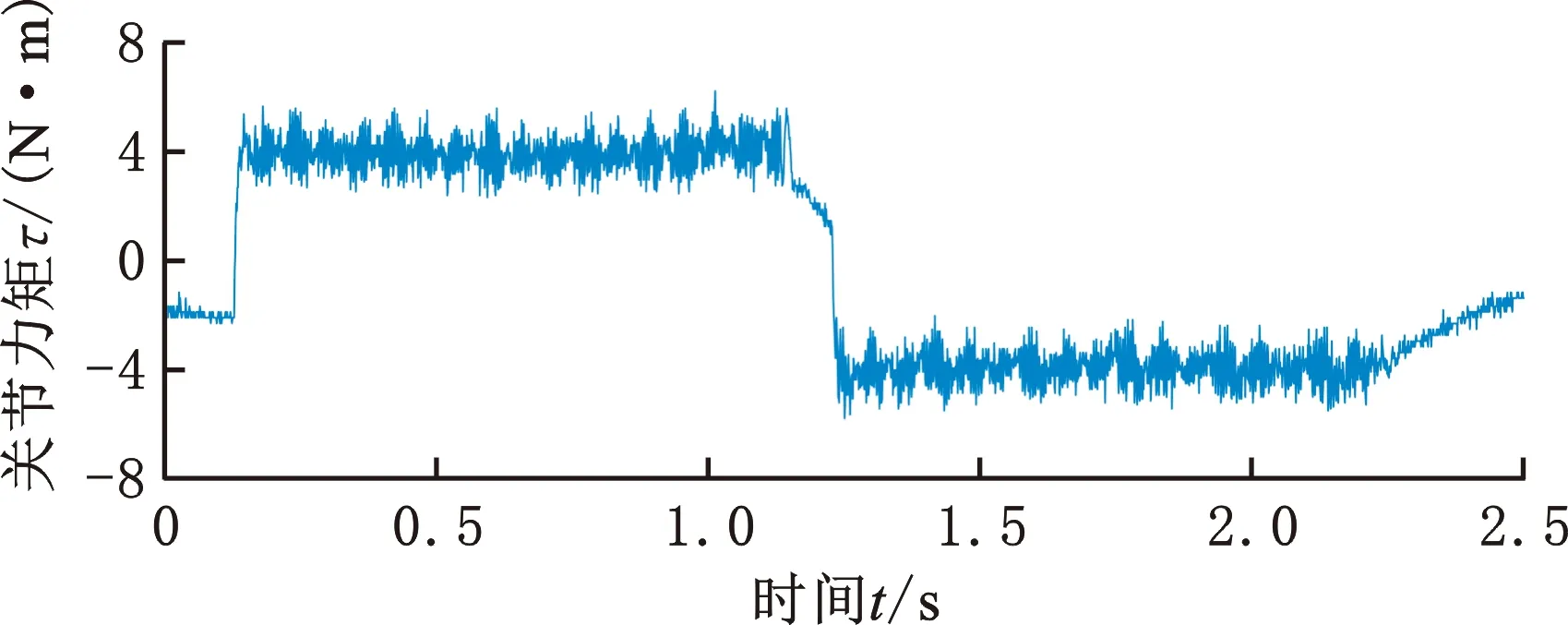
(a)输出力矩

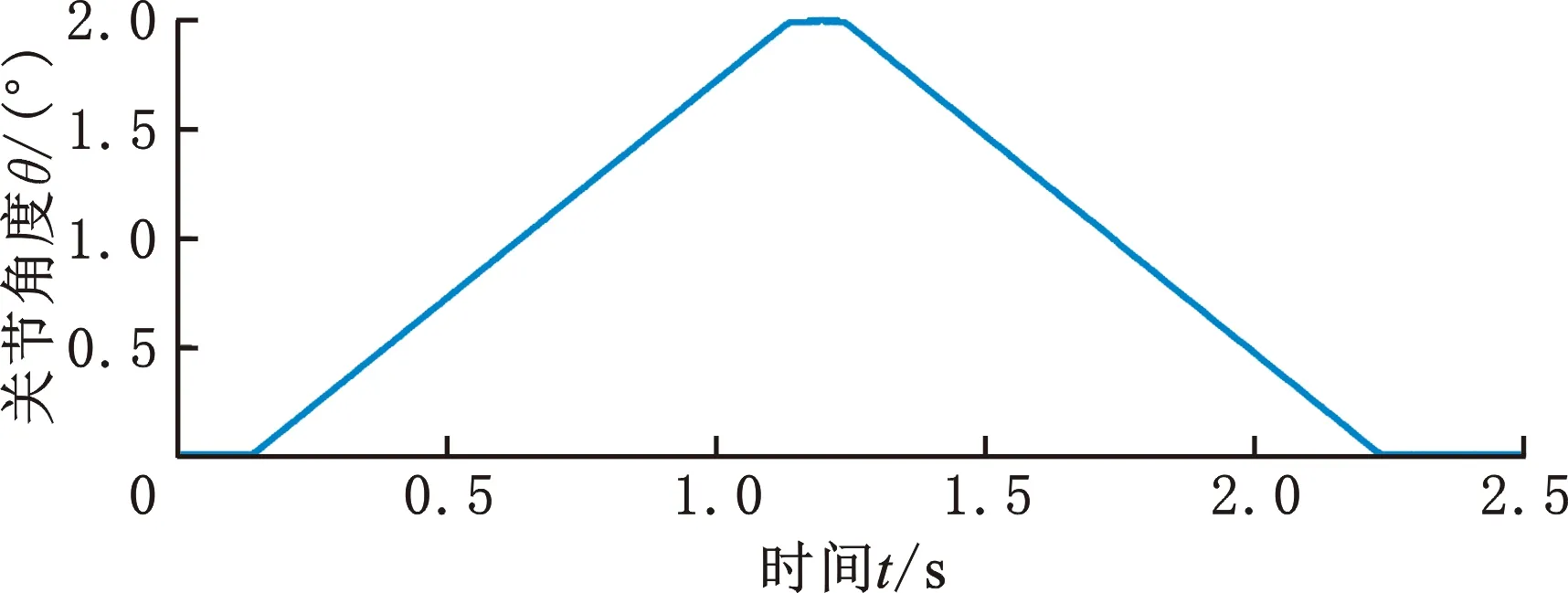
(b)关节角度图3 2°/s时关节输出力矩与关节角度Fig.3 Joint output torque and joint angle at 2°/s

4 实验结果分析

4.1 关节升温效果

为探究不同工作条件下的关节产热量，分别使机器人关节以0.4°/s、2.0°/s、20.0°/s的角速度连续运行，以5 min为间隔测量关节1外壳处温度。为验证理论模型的正确性，对采集得到的温度进行拟合。图4所示为关节外壳实际升温，以及基于式(16)所得的升温拟合曲线。

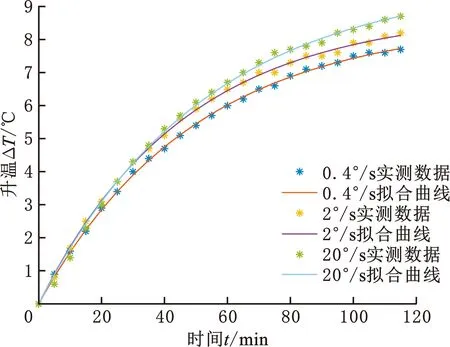
图4 关节升温情况Fig.4 Temperature rise of joints

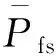
关节角速度分别为0.4°/s、2.0°/s、20.0°/s时，实测温度与拟合曲线对应温度的均方差(RMS)分别为0.0508 ℃、0.0627 ℃、0.1088 ℃。实测温度基本符合式(16)中的理论模型，验证了该模型的正确性。

4.2 关节摩擦力矩变化效果

为探究连续运转状态下摩擦力矩的变化，让机器人按15个不同的关节角速度连续运行115 min，以5 min为间隔采集关节力矩(每组速度的关节力矩有24个测量值)。

图5所示为不同转速的实测摩擦力矩。基于摩擦模型(式(4))，对实测数据进行最小二乘拟合，发现关节转速小于1°/s时摩擦力矩出现Stribeck现象；关节转速大于1°/s时摩擦力矩基本符合关节摩擦模型。机器人实际平稳运行时的关节转速一般远大于1°/s，因此可以忽略其Stribeck现象。

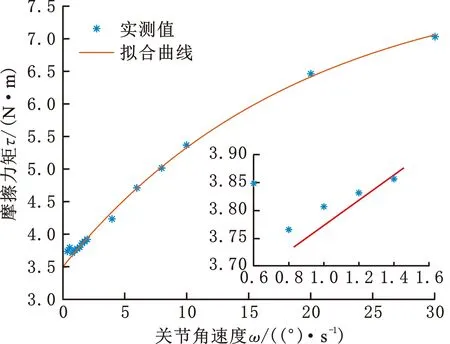
图5 摩擦力矩与关节转速Fig.5 Friction torque and joint speed

为对假设(式(6))进行验证，分别对2.0°/s、20.0°/s转速下的摩擦力矩随温度的变化进行最小二乘拟合。由图6可知，当关节温度在17～26 ℃范围内变化时，尽管摩擦力矩与温度变化成非线性关系，但摩擦力矩-温度曲线的斜率变化不大。因此简化模型时可将摩擦力矩和温度变化近似为线性关系。

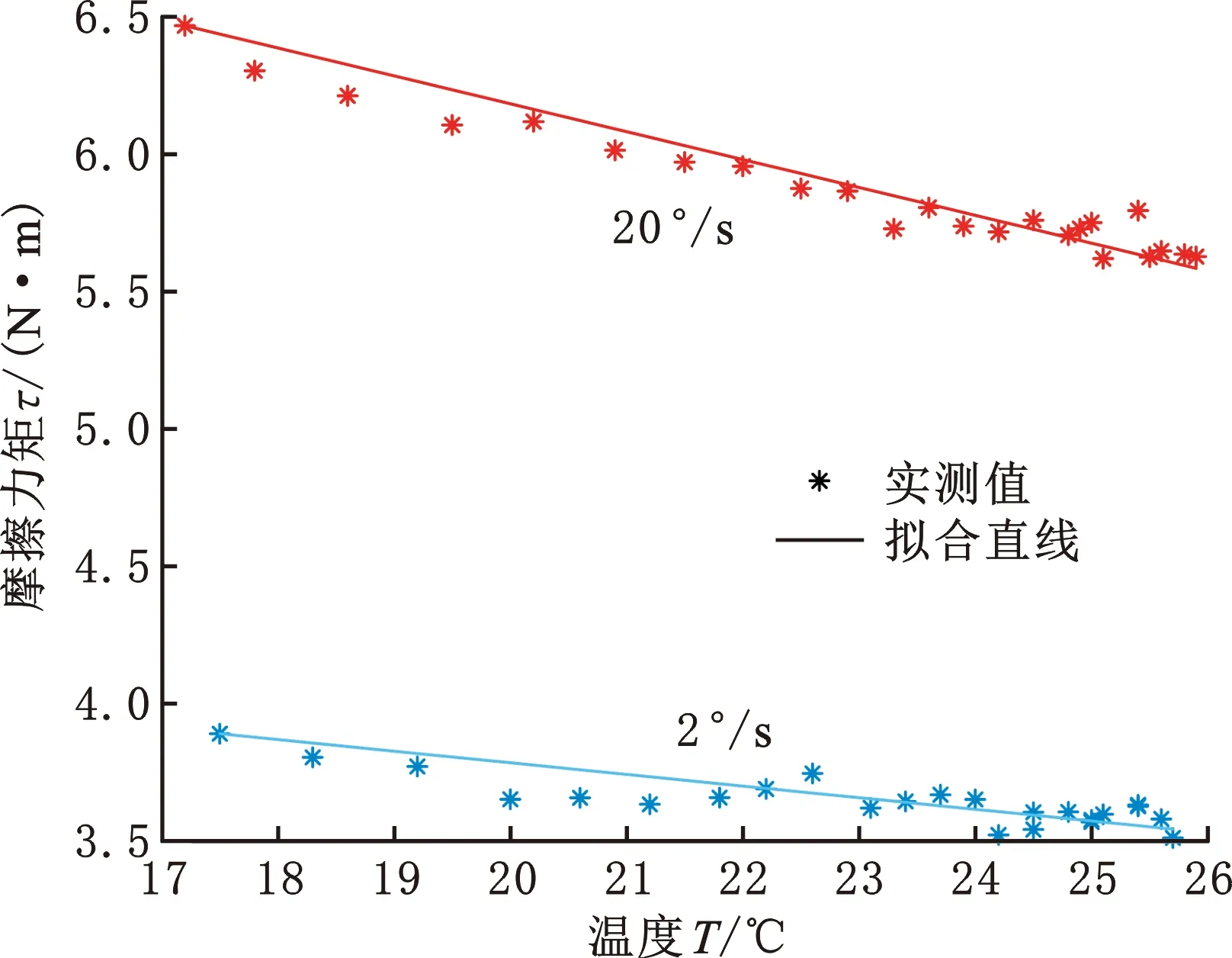
图6 摩擦力矩与温度变化情况Fig.6 Friction torque and temperature change

根据式(16)对关节角速度对应的摩擦力矩进行最小二乘拟合。由图7可知，当关节以10°/s的角速度连续运行时，关节摩擦力矩随时间的增长而减小，实测摩擦力矩与拟合曲线对应摩擦力矩的均方差为0.0283 N·m。实测摩擦力矩基本符合理论模型(式(16))，验证了该模型的正确性。

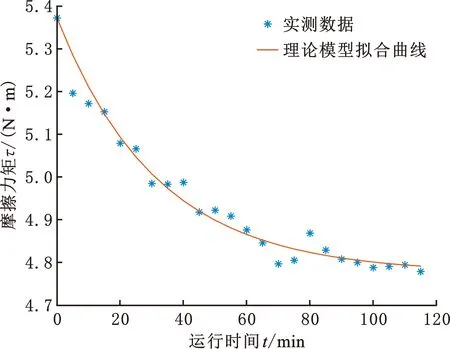
图7 10°/s时摩擦力矩随时间的变化Fig.7 Friction torque changes with time at 10°/s

驱动机器人按照不同速度连续运行，记录各时间点对应的摩擦力矩，可得不同角速度和运行时间对应的关节摩擦力矩，按照式(16)对每个角速度对应的摩擦力矩进行最小二乘拟合。

图8所示为关节角速度1～30°/s内，摩擦力矩随时间的变化，图中的浅色部分为实测摩擦力矩，深色部分为拟合摩擦力矩。速度范围(1～30°/s)内，实测摩擦力矩曲面与理论模型(式(16))的拟合曲面基本一致。

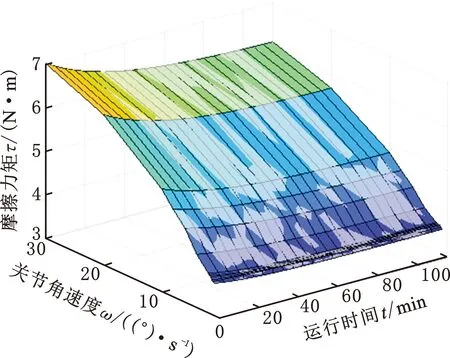
图8 摩擦力矩拟合值和实测值Fig.8 Fitted and measured values of friction torque

4.3 模型验证

为进一步验证摩擦模型，探究机器人完成复杂动作时的关节输出力矩，设计了非匀速轨迹对上述摩擦模型进行验证。

基于机器人动力学模型的前馈控制中，关节前馈力矩的预测精度对控制精度有较大影响，因此，为验证式(16)中的模型效果，驱动全部关节按随机生成的五阶傅里叶级数运动，关节1的轨迹如图9所示。

图9 关节1验证轨迹Fig.9 Verification trajectory of joint 1

关节1的输出力矩包含摩擦力矩、连杆本身运动所需力矩和其他连杆的间接作用力矩。图10所示为机器人由0 min连续运转至115 min时，验证轨迹下关节1的预测力矩和实测力矩。值得注意的是，该随机验证轨迹部分时刻的关节转速不平稳，导致力矩测量值不够精确，因此其验证效果要稍逊于平稳运行时的效果。

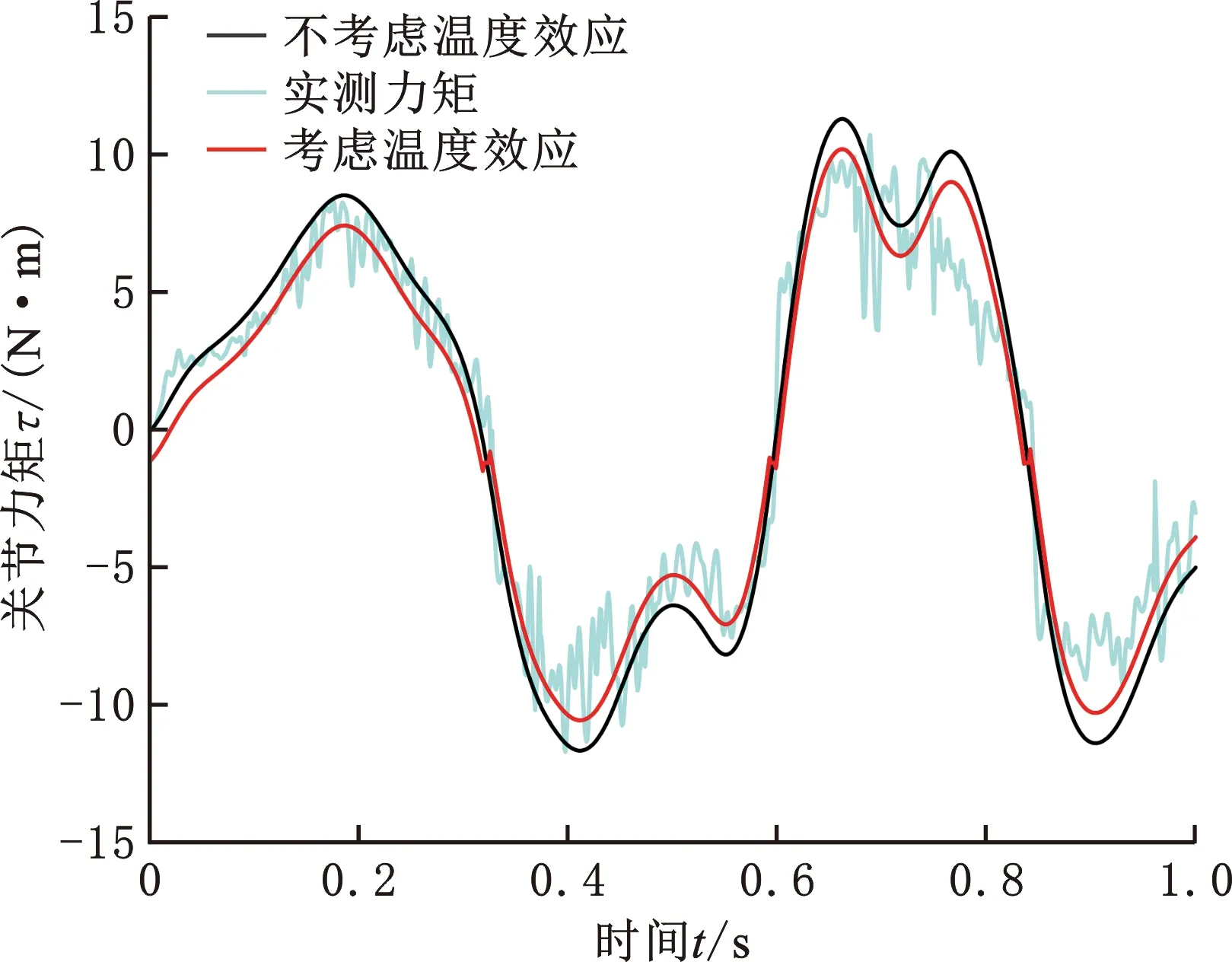
图10 验证轨迹下的关节力矩Fig.10 Joint torque under the verify trajectory

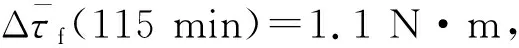
5 结论与展望

本文提出了固定轨迹连续运转状态下的机器人关节摩擦力矩模型。该模型可在无需对关节温度进行测量或预测的前提下，探究温度变化对关节摩擦力矩的影响，并通过实验验证了摩擦模型的可行性，因此该模型可较为准确地描述关节连续运行时摩擦力矩逐渐减小的现象。在实际生产应用中，对于连续重复运动的串联机器人，可基于该模型对摩擦力矩的变化进行预测。

关节发热的原因较为复杂，难以通过数学模型进行准确描述，为简化模型，将运行时的电机损耗等产热功率看作为常量。本文模型忽略了低速状态下的Stribeck现象和加减速度较大时的摩擦迟滞、冲击负荷，因此本文模型仅适用于关节速度变化较为平稳的非低速状态。