基于弧形电容器的浆纱回潮率在线测量

陆浩杰，李曼丽，金恩琪，张宏伟，周 赳

(1.浙江理工大学 纺织科学与工程学院(国际丝绸学院)，浙江 杭州 310018；2.绍兴文理学院 浙江省清洁染整技术研究重点实验室，浙江 绍兴 312000)

浆纱回潮率反映了浆纱的烘干程度，一般棉纱的浆纱回潮率控制在5%～7%，粘胶的浆纱回潮率控制在9%～11%。烘干程度影响浆膜性质(弹性、柔软性、强度、再黏性等)，也影响上浆的能量消耗[1]。浆纱的回潮率主要由上浆机上的组合烘筒控制，烘筒的热量来自烧锅炉产生的水蒸气。传统的上浆工艺要求回潮率越小越好，导致上浆机的能耗巨大且浪费严重[2]，因此亟需实现浆纱回潮率的在线准确测量，以提高浆纱质量，节能减排，减轻纺织企业“碳达峰”压力。

目前浆纱回潮率常用电阻法检测[3]，但其传感器与浆纱直接接触，会引起浆膜损坏。其它方法还有测重法[4]、微波法[5]、红外线法[6]、电容法[7]等。电容法使用电容传感器测量材料介电常数，在纺织领域应用较多的是利用平行板电容器检测纱线条干均匀性[8]和利用同面平板电容器检测织物含水率[9]。如采用平行板电容器测量浆纱介电性能，由于平行板间距较小，浆纱容易与极板接触造成落浆，影响传感器精度和浆纱质量；用同面平板电容器检测时，由于极板间形成的是开放式非均匀散射电场，受到的干扰很多，测量精度不高，因此需要重新设计电容传感器结构，以适用于浆纱的介电性能测量。

本文通过电容法测量浆纱回潮率，设计开发了一种基于弧形极板电容传感器(以下简称弧形电容器)的浆纱回潮率在线检测系统，研究了影响浆纱回潮率测量值的各种因素，并对系统可靠性进行了验证。

1 电容法测量原理

介电常数与材料的含水量之间存在一定的对应关系，使用电容传感器测量浆纱的介电常数，根据被测物的介电常数变化引起电容值变化来实现[10]。

本文设计开发了一种弧形电容器，将2片圆弧瓦片形的金属极板轴向对称放置，极板固定在绝缘材料聚氯乙烯(PVC)圆筒的内表面，PVC圆筒起到屏蔽干扰、保护电极的作用。这种弧形电容器结构小巧简单、易安装，适合用于纱线的介电性能检测。

弧形电容器不同于平行板电容器，这种结构的传感器极板所产生的是非均匀电场，给传感器的理论分析及性能优化带来困难[11]。本文利用保角变换，将弧形极板间的电场分布变换为同面平极板间的电场分布，再利用高斯定理和单元积分法[12]求得弧形极板间散射场的主电容：

(1)

式中：Cx为散射场主电容，F；εx为极板间介质等效介电常数；L为极板长度，mm；t为极板包角，rad。

由于极板边缘效应和接触电极间寄生电容C′的存在，测量电容C通常大于主电容Cx[13]。当电容器的结构和电容检测条件一定，寄生电容C′固定不变，因此通过检测前后2次的测量电容C1、C2可消除寄生电容C′的影响，同时根据式(1)使极板间介质的等效介电常数成为前后2次电容差的函数：

(2)

式中：C1、C2分别为前后2次测量的电容值，F；Cx1、Cx2分别为前后2次测量的主电容值，F；C′为寄生电容，F；εx1、εx2分别为前后2次测量极板间介质的等效介电常数。将式(2)转换为

(3)

假设在弧形电容器内纱线与空气等效为并联关系[8]，则极板间的等效介电常数与纤维介电常数、空气介电常数的关系如下：

εx2=φf2εf2+(1-φf2)εa

(4)

εx1=φf1εf1+(1-φf1)εa

(5)

式中：εf1、εf2分别为前后2次测量的纱线等效介电常数；εa为空气相对介电常数，在常温中通常等于1；φf1、φf2分别为前后2次测量的纱线占电容器的体积分数，%。

纱线体积分数φf由式(6)得到：

(6)

式中：r为纱线半径，mm；r′为极板曲率半径，mm。

最后得到纱线等效介电常数εf2与前后2次测量电容差的关系：

(7)

式中，r1、r2分别为前后2次测量的纱线半径，mm。

当前一次测量的是无纱线空白电容，后一次测量的是有纱线存在的电容时，r1=0，则式(7)变为

(8)

由式(8)可以看出，在电容器结构一定时，纱线的等效介电常数εf2与电容差ΔC=C2-C1成正比，也就是纱线回潮率与电容差ΔC有相关性，这就是电容器测量浆纱回潮率的原理。但是在实际测量中，影响电容值的不仅有浆纱回潮率，还有浆料组成、原纱组成、浆纱线密度、浆液含固率(以下简称含固率)等内因，也有电容器的结构参数、测量电容的LCR(电感、电容、电阻)电桥测试仪参数、环境温湿度等外因。

2 实验系统设计

2.1 硬件设计

本文所设计开发的弧形电容器如图1(a)所示，主要组成部分有绝缘管道、弧形金属激励极板、弧形金属检测极板，激励极板和检测极板尺寸相同，且呈轴向对称放置。图1(b)为横截面结构示意图。图1(c)为硬件系统示意图。电容式浆纱回潮率在线检测系统主要由弧形电容器、LCR电桥测试仪、上位机等单元组成。上浆机上，浆纱经烘房烘干后出来，在靠近经轴处穿过弧形电容器，LCR电桥测试仪测量其电容值，并把数据传到上位机，上位机根据本文构建的模型计算出浆纱回潮率，即能实时测量出浆纱被卷绕到经轴时的回潮率。

图1 硬件设计示意图

2.2 软件设计

系统软件基于LabVIEW开发，由主函数程序、可编程仪器标准命令(SCPI)指令集程序、数据处理程序、数据读取保存等程序组成。在进行测试时，上位机与LCR电桥测试仪通过串口连接，以Modbus RTU协议建立端口通信。开机后系统初始化，设置LCR电桥测试仪参数。然后开始采集，由VISA读取程序读取LCR电桥测试仪传输过来的电容和损耗因数数据，再根据本文所建的模型进行数据处理即可返回实时回潮率值；将实时回潮率值以及平均值、变异系数等显示在波形图表窗口上。停止采集后，可以将所有数据保存为.csv格式文件。完成1组实验后，清零数据和图表，再次开始采集，重复采集和数据处理程序，直到实验完毕停止程序。主程序流程如图2所示。

图2 主程序流程图

3 实验方法

3.1 LCR电桥测试仪参数设置

LCR电桥测试仪测量时可设置的参数有电压、内阻、采样频率和频率。电压选择300、600 mV，内阻选择10、1 000和100 000 Ω，采样频率选择500、1 000和2 000 ms。改变电压、内阻、采样频率3个参数其中之一，在不同频率下测量弧形电容器空白电容值，然后进行对比。

3.2 电容器结构设计

本文所设计开发的弧形电容器结构如图1(b)所示。电容器的结构参数主要有：极板曲率半径r′、极板长度L、极板包角t。选取弧形电容器3个结构参数中的2个作为定值，另一个作为变量，定制若干电容器测量空白电容值。

使用有限元虚拟仿真技术模拟分析不同结构参数条件下的电容值[14]，与实际电容器对照，进一步分析结构参数对传感器性能指标的影响，对传感器结构进行优化设计。

3.3 温湿度设置

固定LCR电桥测试仪测试参数和弧形电容器结构，在不同的温湿度条件下测量空白电容。湿度范围为35%～70%，温度范围为28～50 ℃。

3.4 回潮率及电容值测试

将20、77 tex棉纱，分别用含固率为5%、10%的淀粉浆料在GA392型单纱上浆机上进行上浆，获得4种不同规格的浆纱试样，然后对试样进行调湿。将制备的浆纱试样先烘干处理和称量，然后在不同的湿度条件下预调湿24 h，取出后称量，根据式(9)计算得到回潮率：

(9)

式中：x1为浆纱回潮率，%；m1为浆纱调湿后质量，g；m2为浆纱干态质量，g。

在恒温恒湿环境中，先用弧形电容器测量空白电容值，然后取出不同回潮率的浆纱试样分别穿过弧形电容器测量电容值，检测时长为4 min。

4 实验数据与结果分析

4.1 LCR电桥测试仪与电容关系

图3示出电容对LCR电桥测试仪的频率响应。结果表明，电压、采样频率、内阻3个参数对电容测量结果没有太大影响。电容值受测量频率的影响较大，随着频率的增加而减小，但测试频率过高时，纤维间的水分极化反应反而降低，产生冰冻效应[15]。根据文献[16]的测试方法，在10～10 000 Hz频率范围内测试不同回潮率纱线的电容，对各频率下的电容值和含水率进行线性拟合，拟合得到相应的相关系数R2与频率分布如图4所示。可以看出，在频率4 000 Hz处，相关系数R2最高(0.97)，说明该频率下电容对含水率的响应最显著，因此选择4 000Hz作为测试频率。

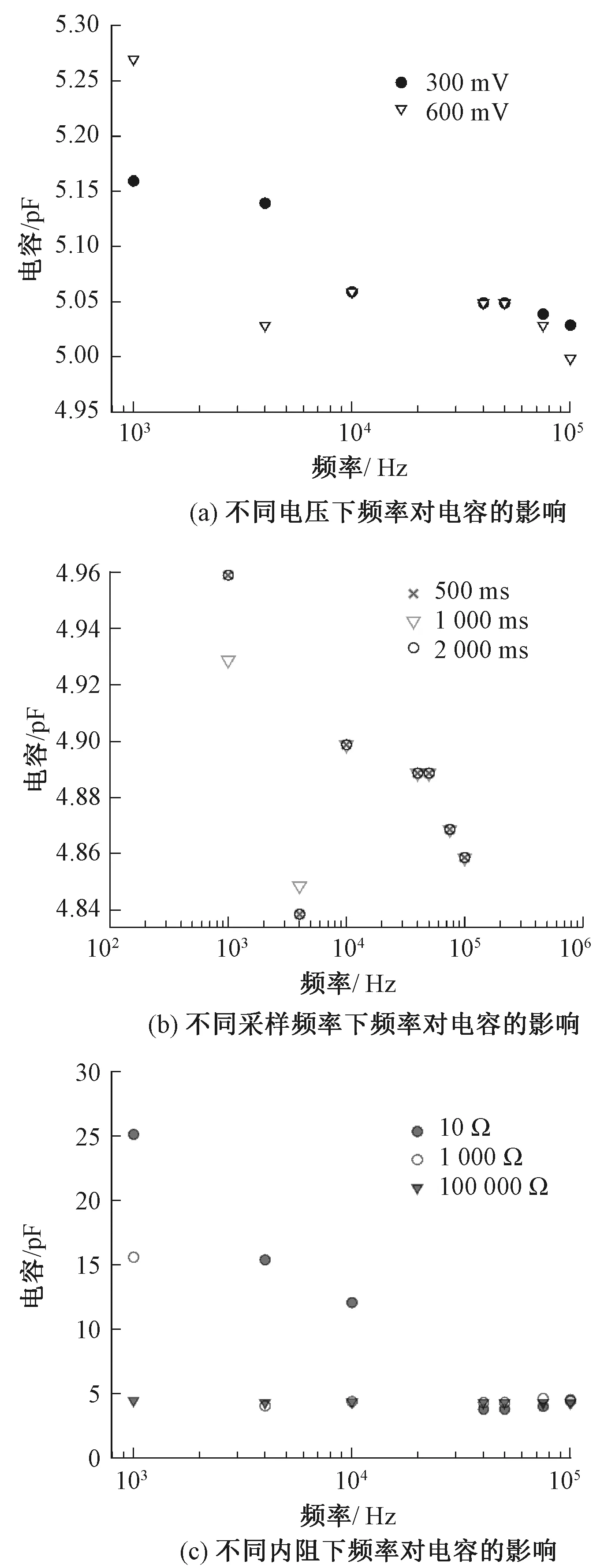
图3 电容对LCR电桥测试仪的频率响应

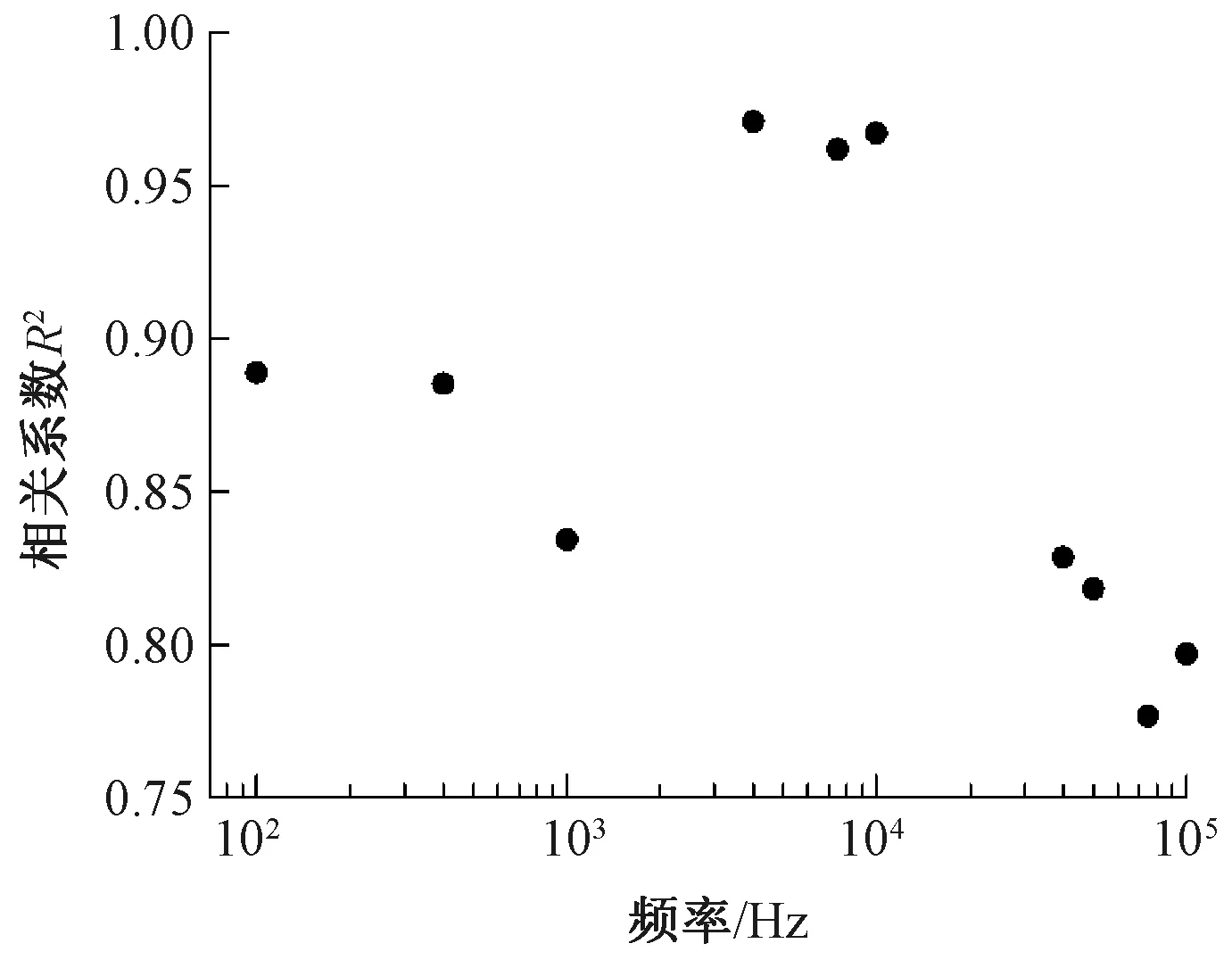
图4 电容对回潮率的频率响应显著性分布

4.2 电容器结构与电容关系

图5示出弧形电容器结构参数与电容的关系。图5(a)显示，随着极板曲率半径的增大，电容减少。由式(1)可知，主电容不随极板曲率半径变化而变化，这是因为极板间的寄生电容随距离增大而减小，从而使测量电容减小。图5(b)显示，极板长度增大，电容增大。由式(1)可知，极板长度与电容正相关。图5(c)显示，极板包角增加，电容也增大。由式(1)可知，极板包角与电容也是正相关。

图5 弧形电容器结构参数与电容的关系

从图5可以看出，利用有限元技术模拟的电容仿真结果与实测结果趋势一致，实测值与仿真值的差别是寄生电容和环境干扰引起的。

以极板曲率半径r′、极板长度L、极板包角t为自变量，以检测场灵敏度变异系数、相对灵敏度、电容量、主电容占比为目标因变量，对弧形电容器进行多目标优化设计。运用有限元虚拟仿真技术和二次回归正交组合实验法，分别对每个因变量目标建立关于极板曲率半径r′、极板长度L、极板包角t为自变量的回归方程。然后构建优化目标函数：

(10)

式中：minF为目标函数；y1为相对灵敏度；y2为检测场灵敏度变异系数；y3为主电容占比，%；y4为电容量，F。

根据实际制作工艺限制，设定约束条件，对式(10)求最小值，获得相应的自变量，最终确定电容器结构参数为：极板曲率半径r′=7 mm、极板长度L=100 mm、极板包角t=8/9π rad，以保证电容器性能的最优化。

4.3 环境温湿度与电容关系

固定LCR电桥测试仪测试参数和弧形电容器结构参数，在不同温湿度环境中测量的空白电容经过插值后生成的温湿度-电容关系如图6所示。LCR电桥测试仪参数设置为：频率4 000 Hz，电压600 mV，采样频率500 ms，内阻100 000 Ω。弧形电容器结构参数为：极板长度1 000 mm，极板曲率半径7 mm，极板包角8/9π rad。

图6 不同环境温湿度下测得的电容

从图6可以看到，环境温湿度对电容值影响复杂。温度的变化会改变某个固定频率的介电性能，变化趋势和频率有关[17]；在湿度较高的情况下，在一定范围内电介质所含水分越多其极化能力越强，进而表现为材料的介电常数增大，电容升高[18]。纱线的回潮率本身与环境温湿度有关，因此电容器需保持在恒温恒湿条件下测量。

4.4 浆纱回潮率、线密度及含固率与电容关系

浆纱试样在调湿后通过弧形电容器测得电容值，结合空白电容值，得到电容差ΔC，结果如图7所示。可以看出，回潮率与电容差呈非线性相关。回潮率增加，凝结在纱线表面和孔隙内的游离水变多，产生强烈的极化反应，电容值增大。

图7 不同回潮率、线密度和含固率的浆纱测得的电容差

本文采用多元回归算法拟合浆纱回潮率、线密度、含固率与电容差的关系，根据由MatLab编写的多元指数回归算法，得到浆纱回潮率、线密度、含固率与电容差的多元回归模型：

(11)

式中：x1为回潮率，%；x2为线密度，tex；x3为含固率，%。

式(11)多元回归模型相关系数R2为0.91，调整后R2为0.91，表明模型拟合度较好。ex1的t统计量为20>2，说明回潮率对电容差ΔC有显著影响；ex2、ex3的t统计量分别为0.49、0.09，表明含固率、线密度对电容差影响不显著，可以剔除。

经优化后得到浆纱回潮率与电容差的指数回归模型：

ΔC=0.279+2.791×10-6ex1

(12)

式(12)回归模型相关系数R2为0.92，调整后R2为0.92，模型拟合度好，拟合曲线趋势与文献[19]的实验结果一致。

5 应用与验证

5.1 模型应用

将式(12)作如下变换：

(13)

可见，只需知道电容差，就可得到回潮率。将式(13)作为函数模型导入浆纱回潮率测量系统中。

在测试前，将弧形电容器放置在上浆机靠近经轴处，使浆纱穿过传感器，如图1(c)所示。开机开始检测，先测量空白电容值并记录，随着浆纱在上浆机上的运动，传感器检测出浆纱吸湿回潮后的电容值。将电容值数据传递至系统，系统根据式(13)计算得到实时的浆纱回潮率并显示在上位机屏幕上。

5.2 验证测试

为验证所建立模型的准确性，对15组试样进行检测，将烘箱法测得的回潮率数据与用本文系统检测到数据进行对比，结果如表1所示。

表1 电容法与烘干法测量回潮率结果比较

从表1可看出，采用本文系统检测的回潮率相对误差最大值为9.66%，平均误差为3.4%，表明基于电容测试指标所构建的回归模型对浆纱回潮率具有较好的预测。

从表1也可看出，采用电容法测量回潮率产生的误差不稳定。一个原因是环境干扰。另一个原因是模型假设电容器内纱线与空气是并联关系，实际情况是纱线类似颗粒集聚状分布于电容器的一定区域内，在弧形电容器非均匀电场内，纱线与空气既有串联又有并联，复合关系复杂。

6 结 论

1)本文设计开发了一种电容式浆纱回潮率在线检测系统，其核心部件为弧形极板电容传感器、LCR电桥测试仪及上位机。弧形极板电容传感器结构小巧简单，成本低廉，可非接触式地测量纱线的介电性能。

2)电容值受LCR电桥测试仪测试频率的影响较大。随着电容器极板曲率半径的增大，电容值减小；极板长度增大，电容值增大；极板包角增大，电容值也增大。环境温湿度也会对电容值产生复杂影响。浆纱回潮率对电容值的影响显著，浆纱线密度、浆液含固率的影响不显著。

3)建立了电容差与浆纱回潮率指数回归模型。在上浆机上使用电容式浆纱回潮率在线检测系统对浆纱回潮率进行测量，其结果与烘箱法测量结果相比平均误差小于5%，有一定工程实用价值。