双轴精密运动平台的IMMPDA滑模同步控制研究
付炳臻
(辽宁机电职业技术学院,辽宁 丹东 118009)
双轴精密运动平台是一种特殊的笛卡尔结构,其机械结构简单、稳定性高,广泛应用于精密测量、数控加工等领域[1]。该平台在平行方向上分别安装了一台永磁直线电机,并推动横轴进行运动,其具有行程大、驱动力大、负载高等优点,缺点是在平台运动过程中存在高精度的位置同步误差,导致加工精度低[2]。基于此,本文以直线电机双轴精密运动平台为研究对象,对高精度工况下双轴精密运动平台直线电机数学模型与同步控制等方面展开研究。提高双直线电机加工精度的方法有卡尔曼滤波、迭代学习控制等,但卡尔曼滤波只针对单轴控制,并不能实现双轴同时控制[3];迭代学习控制则收敛速度慢,很难在有限的时间内将误差收敛为0[4]。因此,本文提出了一种双轴精密运动平台的IMMPDA滑模控制器,该控制器不仅具有同时性,而且具有一定的收敛特性,最后通过实验结果验证了本文所提出的控制方法是有效可行的。
1 双轴精密运动平台数学建模
通过分析永磁直线电机工作原理[5-10],得出双轴精密运动平台的平行轴的电磁推力和机械运动方程分别为:

式中,Kfi是电磁推力系数;iqi是q轴电流;npi是磁极对数;λPMi是永磁体磁链;τi是极距;下标i=1或2,表示双轴精密运动平台的两个平行轴。
根据式(1)的电磁推力,PMLSM机械运动方程可表示为:

式中,Mi为动子总质量;vi为动子速度;Bi为粘滞摩擦系数;Fi为扰动,包括电极端部效应、参数变化、系统外界扰动及非线性摩擦力等。
由式(1)和式(3)可得,理想状态下的双轴精密运动平台的单轴动态方程为:
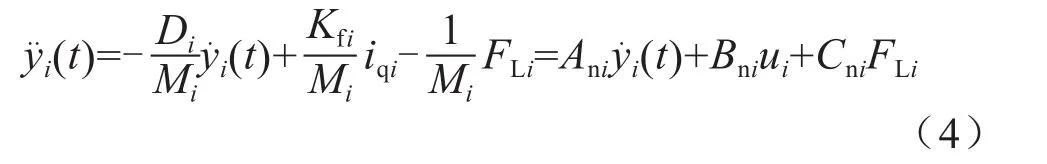
式中,yi(t)为动子位置;Ani=-Di/Mi,Bni=Kfi/Mi,Cni=-1/Mi;ui为控制器输出,ui=iqi,即q轴电流。在考虑各种因素干扰存在时,式(4)的动态方程变为:
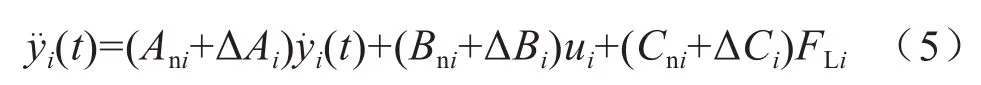
式中,ΔAi、ΔBi和ΔCi为系统参数Mi和Di所引起的不确定量。
Hi为系统不确定性的总和,表示为:
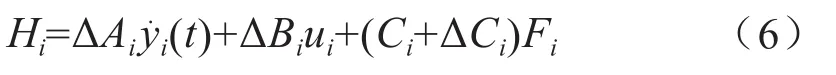
这里假设Hi有界,即|Hi|≤ρ,ρ为正常数。
2 IMMPDA算法流程
为增强双轴永磁直线电机的同步性,采用如下模型实现交互过程。交互混合概率为:

式中,i,j=1,2。归一化因子为:

k-1时刻交互后的初始第j个模型的最优估计和协方差分别为:
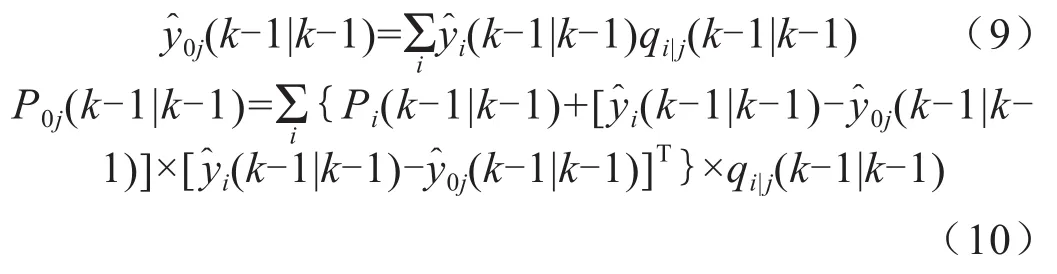
式中,k代表当前时刻,k-1代表上一时刻。
滤波过程为:

状态一步预测误差自相关矩阵为:
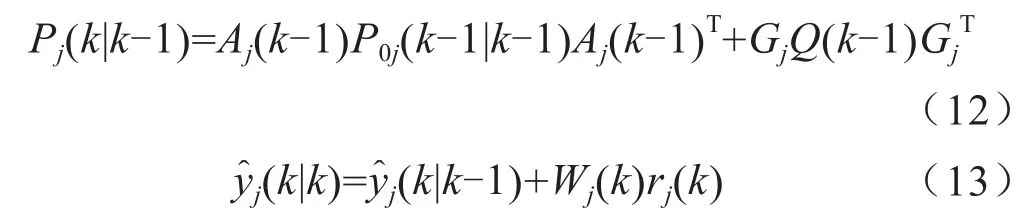
式中,W为滤波增益;r为预测位置误差;Q为新息矩阵。
误差自相关矩阵为:
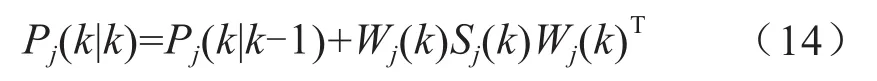
式中,S为新息协方差矩阵。
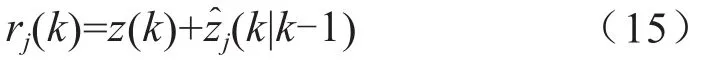
预测位置误差为:根据预测的状态量计算对应的观测量为:式中,H为观测矩阵。

计算新息协方差矩阵为:
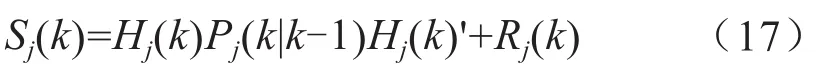
式中,R为观测协方差矩阵。
计算增益为:
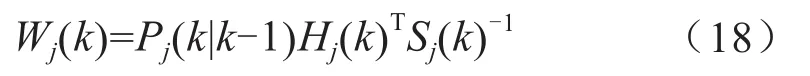
正态分布函数为:
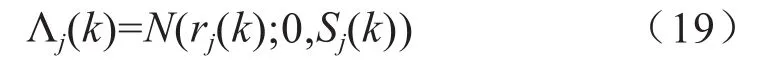
第j个模型发生的概率为:

根据上述公式,得出k时刻的位置输出和斜方差表达式分别为:

3 滑模控制器设计
在双轴精密运动平台的系统中[11-15],考虑到两平行轴间的位置同步误差,首先定义位置同步误差及其导数为:

式中,ym(k)为理想的位置信号;i=1,2,代表平台的两个轴。
设计滑模函数为:

式中,c>0。定义Lyapunov函数为:
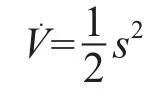
则:

且:
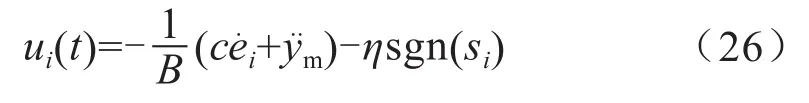
则:

从控制率的表达式可知,当干扰Hi较大时,为了保证鲁棒性,必须保证足够大的干扰上界。
4 仿真实验和分析
PMLSM的推力系数K=15.8 N/A,定子电阻参数R=2.5 Ω,动子质量M=8.2 kg,粘滞摩擦系数D=4 N·s/m。采用MATLAB/Simulink搭建控制算法模型以及平台模型,并进行仿真实验。为了验证所提出的控制策略的有效性,对比只加滑模控制器的位置同步误差效果和系统在加入干扰后所影响的程度。在仿真中输入的位置响应为ym=0.06sin(πt)m的正弦信号,由此验证所提出的IMMPDA滑模控制器可以有效地提高位置同步的误差精度。
为了描述更加具体,将双轴分别用Y1轴和Y2轴表示。在未加任何控制器的时候,Y1轴与Y2轴位置同步误差如图1所示。由图1可以看出,误差非常高,还没有达到加工出精密器件的标准。

图1 未加控制的双轴同步误差
在只加滑模控制器的情况下,在2 s时突加额定负载FL=65 N,Y1轴与Y2轴位置同步误差如图2所示。由图2可以看出,误差基本接近于0,并且在受到干扰后,同步误差恢复时间只需要0.02 s左右。
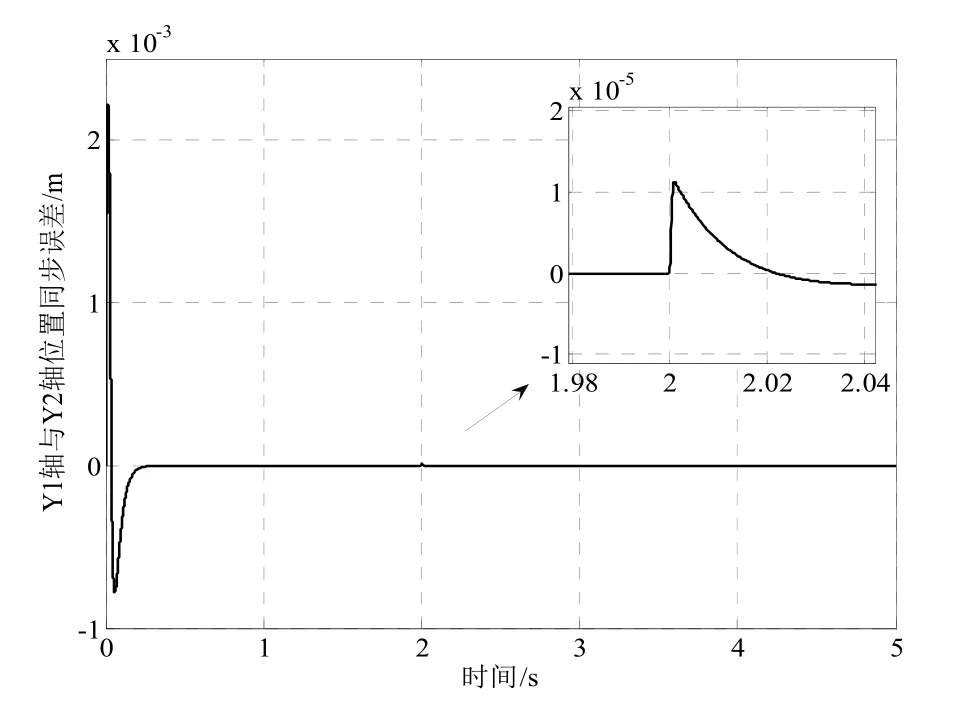
图2 滑模控制器下的双轴同步误差
加入IMMPDA滑模控制器后,在2 s时突加额定负载FL=65 N,Y1轴与Y2轴位置同步误差如图3所示。由图3可以看出,在施加相同负载时,位置同步
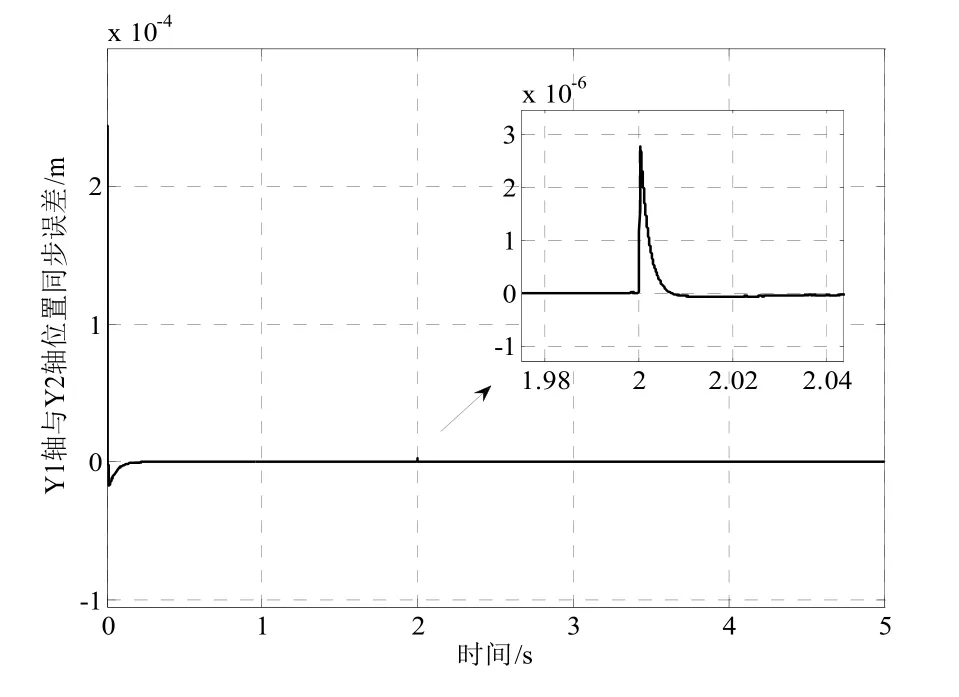
图3 IMMPDA滑模控制器下的双轴同步误差
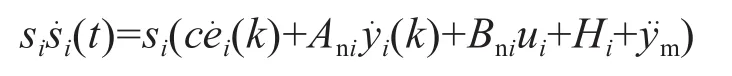
为了保证(t)<0,设计滑模控制率为:误差由1.1×10-5m减小到了2.8×10-6m。
根据图1、图2和图3可知,IMMPDA滑模控制可以有效提高双轴同步误差精度,并且在受到干扰后缩短了恢复时间。
5 总结
本文首先对双轴精密运动平台进行建模,其次对位置控制器采用IMMPDA进行滤波,并用滑模控制器对其进行控制,经过仿真分析得出,该控制方法提高了同步误差精度,并且在误差收敛速度上得到了显著提升,提高了系统的鲁棒性,削弱了外界扰动等不确定因素对系统的影响。

