换个角度看问题

甄玺

在做练习时，我发现有两道值得探究的题目：

问题1：如图1，将一条长为60cm的卷尺铺平后折叠，使得卷尺自身的一部分重合，然后在重合部分（阴影处）沿与尺边垂直的方向剪一刀，此时卷尺分为了三段，若这三段由短到长的比为1∶2∶3，则折痕对应的刻度有_________种可能。

三段线段之比为1∶2∶3，则三段长度分别为10cm、20cm、30cm。若分类讨论，如图1，把三段线段记为第一段、第二段、第三段。则通过分类讨论可得：

（1）若第一段长为10cm：①第二段长为20cm时，折痕处是20cm；②第二段长为30cm时，折痕处是25cm。

（2）若第一段长为20cm：①第二段长为10cm时，折痕处是25cm；②第二段长为30cm时，折痕处是35cm。

（3）若第一段长为30cm：①第二段长为10cm时，折痕处是35cm；②第二段长为20cm时，折痕处是40cm。

综上所述，折痕的位置有4种，即在20cm、25cm、35cm、40cm处。而此题的难点与重点是：这里指的第二段的长度是我们肉眼能看到的第二段长度的2倍，而第三段也有一小部分被第一段覆蓋，解答时，得先理清这三段的长度。此外，这里还有“剪断处”与“折痕处”两个概念要理清，不然无法得出正确的解答。

我觉得这道题我们还可以换种眼光来思考。

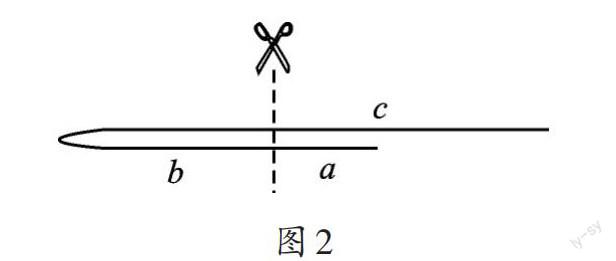
题中只对卷尺的长度进行了描述，而没有提到卷尺的宽度，如果把卷尺抽象成一条线（如图2），这三段长度分别记为a、b、c，而折痕处是（a+[b/2]）。

（1）当a=10cm：①b=20cm时，折痕处为20cm；②b=30cm时，折痕处为25cm。

（2）当a=20cm：①b=10cm时，折痕处为25cm；②b=30cm时，折痕处为35cm。

（3）当a=30cm：①b=10cm时，折痕处为35cm；②b=20cm时，折痕处为40cm。

同样也得到了相同的答案。显然，把图抽象成线之后，几个无法理清的难点就变得相对简约了。换个角度思考，说不定就可以另辟蹊径，打开新的解题方向与思路。

还有另外一道折叠类问题。

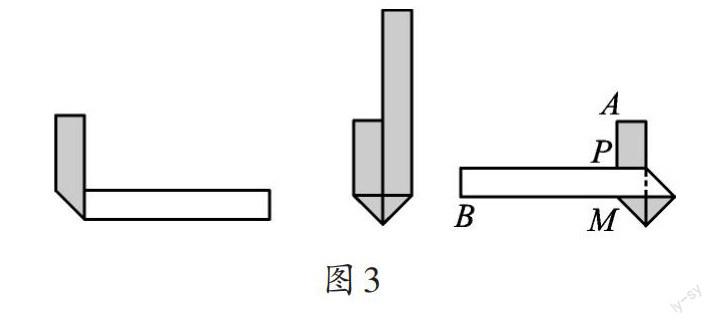
问题2：有一根长30cm、宽3cm的长方形纸条，我们将其按照图示的过程折叠（如图3），为了美观，希望折叠完成后，纸条的两端超出点P的长度相等，则最初折叠时，MA的长应为_____________cm。

我找一张长方形纸条，在纸条上标出A、M、B，照着题目的要求折叠，再展开（如图4）。设PA=xcm，则AM=（x+3）cm。中间有折痕的地方长度为9cm。题目要求两段超出长度一样，得到方程2（x+3）+9=30，解得x=7.5。所以MA=x+3=10.5（cm）。

我不禁思考，不折纸，能解决这个问题吗？

看图3的最后一张图，折叠完毕后的纸条有3个三角形与2条线段。每条线段的长就是AM的长；每个三角形展开都是一个腰为3cm的等腰直角三角形，加起来总共是9cm。那么多出来的21cm分成了2个（x+3）cm，所以x=7.5，则MA=10.5cm。

看吧，知其然，更要知其所以然，不折纸，也能求出答案。

小伙伴们，我们在数学王国中畅游时，尝试从不同角度发现问题，用不同方法解决问题，定能发现数学之妙哦！

教师点评

数学源于生活，又高于生活。我们在平时生活中应多积累数学经验，并从实践中提炼出数学问题，找到解决之道。小作者能从不同的角度对问题进行剖析与思考，能把“图形”抽象成“线段”，化繁为简，让问题解决更明晰；把“折叠”问题展开成“线段”问题，并将不同类型的问题整合在一起，进行对比分析，将所学的数学知识活学活用。相信小作者继续用别样的角度观察世界，能更好地体会到数学之美。

（指导教师：章薇薇）