初中数学课堂导入方式的探究
江苏省南京师大附中树人学校 王 磊
如果说教育是一门艺术,那么课堂导入就是一种创造[1].课堂伊始,利用新颖方法导入能有效唤醒学生的智力情绪,让学生产生浓厚的学习兴趣,使得课堂渐入佳境.因此,导课方式不仅体现了教师的教学基本功,还能活跃课堂气氛,推进课程进展.
一本引人入胜的好书往往有着精彩的序言,一篇好的文章往往有个好的开头.同样,数学课堂的导入,也需要有新颖、引人入胜的方法,以激起学生的学习热情,让学生以最好的状态投入到新知的学习中.因此,精彩的课堂导入既能体现教育的艺术,又能体现数学独有的创造力.
1 开门见山,直击目标
随着新课改的推进,课堂中出现了很多新颖的教学手段.教师要有一双火眼金睛进行甄别,以确定什么时候该采取哪种教学方式更为妥当.实践告诉我们,对于有些知识,与其绕一个大圈子去吸引学生的注意力,还不如开门见山地直接呈现来得效果好.
开门见山地直接导入需建立在学生对教学目标有所认识的基础上,教师将本节课的教学内容直接呈现给学生,让学生将注意力都集中到知识的学习与探索中,从而提高学生的专注力与自主力[2].
案例1“有理数减法”的教学
“有理数的减法”是七年级的教学内容,学生之前对有理数已经有了比较完整的认识,并掌握了其加法运算的法则.减法的学习对于初中生来说,难度并不大,本节课教学重点是将减法转化为学生所熟悉的加法即可.因此,也可以简单地理解为有理数的减法是加法的延伸.
为此,笔者首先带领学生回顾了有理数加法的运算,要求学生完成以下几个计算:(-9)+(-4);(+4)+(-2);(-8)+2;(-5)+65;(+5)+(+5).
学生顺利解题后,教师直接揭示有理数减法的法则:减某一个数,等于加这个数的相反数,即a-b=a+(-b).
大部分学生对这个定义充满了探究兴趣,几个活跃的学生表示这个运算法则有点意思,迫不及待地想要尝试.笔者精选了几道计算题,供学生试试身手.

此时,教师高度赞扬学生一点就会的聪慧,同时鼓励学生思考:有理数减法与加法之间具有怎样的关系?
学生在自主思考中逐渐完成本节课的教学目标,并在不知不觉中就突破了教学重点与难点.开门见山的课堂导入方式不仅没有让学生产生厌烦感或枯燥感,反而有效地激起了学生自主探究的欲望,为培养学生的学力奠定了坚实的基础.由此可见,课堂导入并非花样越多越好,而应根据实际教学内容,进行合理选择,有时最简单的反而是最合适的.
2 数学故事,引人入胜
我们接触到的数学知识均是经过历史的洗礼,逐渐抽象而来.每个知识都经历了一段又一段的历史演变与发展的过程,尤其是一些令人钦佩、值得颂扬的数学小故事能刷新学生的认知,为培养学生形成良好的思维品质与人生观奠定基础[3].因此,在教学中,可精选一些催人奋进的故事与学生分享,以调动学生学习的积极性,并在数学教育中渗透德育教育,以提升学生的数学核心素养.
案例2“平面直角坐标系”的教学
“平面直角坐标系”是一个对数学学习具有重要影响的知识点,但这又是一个相对枯燥与抽象的知识点.因此,正式授课之前,笔者以笛卡儿的故事吸引学生的注意力,让学生先对此知识产生良好的情感倾向,以削弱学习的枯燥与乏味.
故事情境:年轻的笛卡儿是一位军人,一天他在睡梦中看到许多数学家,有阿基米德、毕达哥拉斯、欧几里得、希伯索斯等.他们正在一起讨论“如何将一个平面内的点和数联系到一起”,因为讨论得太投入,竟然没有人注意到笛卡儿这个不速之客.此时,笛卡儿捡起地上的一把钥匙,轻轻打开了屋内的一扇门,正当他走进去时,梦竟然醒了.(学生都被笛卡儿的梦境所吸引,一个个兴致盎然地期待教师继续说接下来发生了什么.)醒来的笛卡儿迷迷糊糊地睁开眼,看到月光投射到墙角的一张蜘蛛网上,突然灵光一闪,一个念头划过脑际:若蜘蛛是一个点,它可沿着蜘蛛网上下左右来回移动,那么蜘蛛网岂不是纵横交错的线?蜘蛛爬到哪个位置,就可以用两个数字来表示了.由此,驰骋于数学界的平面直角坐标系就产生了.
每个学生都被笛卡儿神奇的梦境与伟大的发明所震撼,趣味性的历史故事快速吸引了学生的注意力.在接下来的学习中,因学生对平面直角坐标系有着一定的情感倾向,导致学习进程尤为顺利,每个学生对该知识的学习都倍感亲切,从而积极主动地参与探索与思考.因此,利用历史小故事的课堂导入,不仅给课堂增添了趣味性,还有效地拉近了学生与知识的距离.
3 活动开展,引发探究
心理学与教育学共同研究表明,人类对新知的认识与建构,主要是在实践过程中思维呈螺旋式上升而达成.因此,这就要求教师在教学中,设置一些落在学生最近发展区的操作活动,让学生在充足的时间与空间内通过实践操作,完成对知识的认识与理解.如此,则能让学生更加具体、深刻地理解教学内容,掌握所学知识.
案例3“立体图形与平面图形”的教学
立体图形与平面图形的内容比较抽象,若教师以传统的授课模式讲解,学生很难从根本上理解立体图形展开后,如何获得相应的平面图形.因此,笔者以活动导入的方式,让学生在直观操作中充分认识二者之间的联系.
活动准备:立方体纸盒、剪刀、水彩笔、磁吸、立体图模型、多媒体等.
活动设计:运用小组合作学习方式让学生在自主操作、观察中探究、感知数学活动的乐趣,体验成就感.
活动过程:
(1)要求学生将正方体的相对面分别涂上相同的颜色,每个对立面之间的颜色不一样.
(2)独立将自己手中的正方体剪开,按照自己的想法去剪,剪开后的图为一整张图形即可.
(3)以小组为单位,观察组内成员的展开图,同时思考两个问题:①有多少种不同的展开方式?有没有一定的规律性?②观察展开图中相对的面是否存在某种规律?
师:哪个小组愿意展示一下本组的正方体展开图?
组1:如图1,我们组展开后得到六种图形.

图1
师:大家看看这六组图形与你们组的一样吗?
组2:有一样的,也有不一样的,我们组还出现了以下三种图形,如图2.

图2
组3:除了以上九种之外,还有两种图形他们两组都没有展示.
师:哦?哪两种?
(组3展示图3)
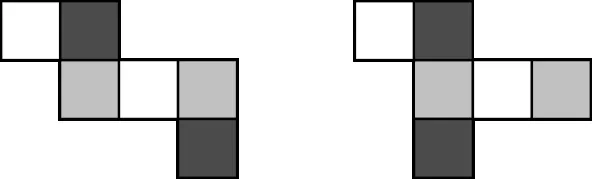
图3
师:还有补充的吗?
(众生摇头)
师:我们来观察这些图,看看是否存在什么规律?
生1:我们可以把图形重新排列.四格在一条线上的排在一起,如图4;其他的排一起,如图5 .

图4

图5
观察可得以下规律:①四方一线两相望;②一马单腿两阶梯.
师:很好!相对的面之间存在什么规律?
生2:同一行或列中间隔一个其他的颜色,若不在同一行或列的,就没有公共的顶点.
…………
此活动的导入既尊重了学生之间的认知差异性,又有效地发展了学生多元化的数学思维.每个学生按照自己的习惯剪开正方体纸盒,并通过小组合作学习的机会观察同伴的展开成果,发现一个普通的正方体展开后竟然有多种不同的图形;再观察图形相对面的规律,以对展开后的图形产生深刻认识;同时,学生在合作中也积累了良好的活动经验,有效地提升了自身的数学理解能力与实际操作能力.
总之,为了适应时代需求,教师需结合授课内容与学生实际情况,灵活选择合适、合理的课堂导入方式,以激发学生的探究兴趣,为课堂的有效性奠定基础.
——笛卡儿自由意志理论探析

