基于Copula理论的多部件系统剩余寿命核密度预测方法
石 慧,康 辉,赵李志,董增寿
(太原科技大学 电子信息工程学院,山西 太原 030024)
0 引言
剩余寿命(Remaining Useful Life, RUL)预测是制定最优维修决策的前提和保证。根据剩余寿命预测结果提前进行维修准备,可以有效减少故障的发生,进而提高系统的可用性和可靠性,降低或避免故障造成的重大损失,同时减少维修保障费用,具有重要的研究意义和实用价值[1-3]。
剩余寿命预测是系统故障预测和健康管理领域的核心[4]。AHMADZADEH等[5-7]对剩余寿命预测建模方面的研究进展进行了综述,其方法主要包括物理模型的方法、基于专家知识的方法和数据驱动的方法等。对大多数系统而言,难以建立准确的物理模型表征复杂系统的退化及故障的机理,同时获取有关系统完整的专家知识成本较高,而数据驱动方法仅依赖于观测数据,因此它们更常用于RUL预测中[8-9]。
现有的许多数据驱动实时剩余寿命预测方法需要进行模型结构假设及参数估计,需要假设其作为判断依据的随机取值的样本符合某种特定模型结构,这些模型结构的假设与实际的物理模型之间常常存在较大的差距,同时参数估计的最优化过程有可能收敛到局部最小而不能保证全局最优[10],因而预测模型将不能保证最终渐近收敛于真实的样本模型。基于深度学习的数据驱动预测方法有强大的特征自学习能力,不需要事先对未知的退化模型进行假设,但其内部网络结构不能清楚地表征系统退化特征的变化[11]。核密度估计(Kernel Density Estimation, KDE)不需要对数据分布进行假设,完全从数据出发研究分布特征,是一种非参数估计方法[12]。BORTOLOTI等[13]提出一种基于k均值的监督学习聚类方法,称为监督核密度估计k均值,将核密度估计用于数据分类。HU等[14]利用核密度估计方法来建立风速的概率密度函数模型,通过与参数估计模型的比较验证了该方法的准确性。GUAN等[15]提出一种基于改进的核密度估计模型的检测算法估计风电机组的可靠性。张卫贞等[10]针对单部件系统建立相应的核密度估计模型,并进行寿命预测。但其仅针对单部件的退化过程及其剩余寿命预测展开研究。
大型复杂系统往往是由相互作用的多个部件组成,部件之间的相互依赖关系是不可忽略的。多部件之间的相互依赖关系包括经济相关性、结构相关性和随机相关性[16]。随机相关性影响着部件的退化状态和剩余寿命分布,是维修相关性产生的原因[17],因此考虑随机相关性影响的部件剩余寿命预测可以更为准确地反映系统的退化规律和未来状态[18]。在以往的研究中,许多描述多部件系统相关性的可靠性模型是通过研究部件失效对其他部件性能的影响来建立的[19]。但在实际系统运行过程中难以获得故障率,部件发生故障之前的各部件的连续退化状态与实时剩余寿命的相关性在研究多部件系统预测与健康管理问题中更值得关注。针对多部件系统部件间相关性的建模,常用的方法有多维退化模型[20-21]、退化率相关模型[22-23]和基于Copula函数的退化相关模型[24-28]。多维退化模型一般采用多维正态分布来描述系统中各部件的退化过程,退化率相关模型仅考虑部件间随机相关性对退化率产生的影响,忽视了其对部件退化状态造成的影响,Copula函数相较于前两种方法,在具体的多变量模型未知的情况下,可以灵活地构造多变量分布,是一种有效而灵活的随机变量间相关性建模方法,近年来被广泛应用于可靠性和剩余寿命建模中。LI等[24]利用Lévy Copula函数建立了多部件系统在相同环境下考虑部件间随机相关性的可靠性模型。盖炳良等[25]和YANG等[26]利用Copula函数建立了的随机相关的两部件系统退化模型。杨志远等[27]基于伽马过程建立系统退化模型,使用Copula函数描述退化过程的相关性,进行系统可靠度分析和剩余寿命预测。WANG等[28]提出一种基于维纳过程的产品RUL预测方法,其相关性用Frank Copula函数来表征。但对于不同的应用问题,尤其存在连续退化随机相关多部件系统,很难建立一个剩余寿命预测模型完全包含所有复杂系统的情况。
综上所述,本文依靠传感器获得的实时监测数据,考虑多部件系统连续退化过程中部件间随机相关性影响,提出一种基于Copula理论的多部件系统非参数核密度剩余寿命预测方法。首先基于核密度估计求得部件的退化分布函数;然后采用Copula函数进行部件随机相关性建模,利用赤池信息准则选择最优的Copula函数,避免了不同类型的Copula函数可能导致的预测结果不准确的问题;最后建立连续退化过程中随机相关性影响的多部件系统非参数核密度剩余寿命预测模型并通过齿轮箱试验台进行试验,验证了所提模型的有效性和准确性。
1 基于非参数核密度估计的退化分布
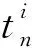
(1)
式中:hn为部件i选用的核函数窗宽,n为部件i的单位退化增量的样本数,K(·)为部件i选用的核函数。
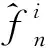
(2)
窗宽hn影响拟合效果,对概率密度函数估计的准确性具有较大影响。取值过大时,平均的影响突出,使密度函数的细节变得模糊,不能清楚地反映密度函数的特点;若取值过小,随机性的影响会增强,使密度函数变的不光滑,不能很好地反映密度函数的趋势。因此,随着样本数据的变化可采用均方误差最小准则来选取最优的窗宽,进而准确估计其概率密度函数。常用的准则包括积分均方误差准则(MeanIntegratedSquaredError,MISE)和渐进积分均方误差准则(AsymptoticMeanIntegratedSquaredError,AMISE)。AMISE可以更精确地平衡偏差项和方差项的阶数,更适合应用于核密度估计中最优窗宽的计算[30],因此采用极小化AMISE来求解窗宽的最优解。其表达式为:
(3)

hopt=argminhAMISE(h)=
(4)
(5)
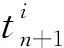
(6)
相应的累积退化概率密度函数为:
(7)
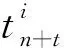
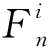
(8)
(9)
(10)
2 考虑随机相关性的剩余寿命建模
2.1 退化之间的相关性分析
建立部件间退化相关性模型,首先需要分析系统各部件之间是否存在相关性。常用的相关性分析方法有Pearson系数、Kendall系数和Spearman系数。Pearson系数具有很好的捕获线性相关性的能力,但在非线性相关噪声方面表现较差;Kendall秩相关系数用于测量两个有序数列之间对应程度的非参数统计量,对于非高斯噪声,Kendall秩相关系数比Pearson相关系数更适合,并且表现出比Spearman秩相关系数更强的鲁棒性和有效性[31-33],因此选择Kendall系数进行部件退化的相关性分析。Kendall秩相关系数τ是衡量系统中各部件之间相关性的重要指标,τ的取值范围为-1~1,当τ为0时,表示两个随机变量相互独立。
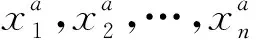
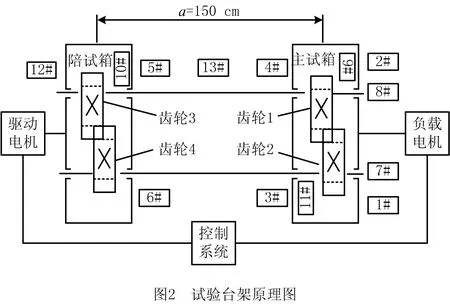
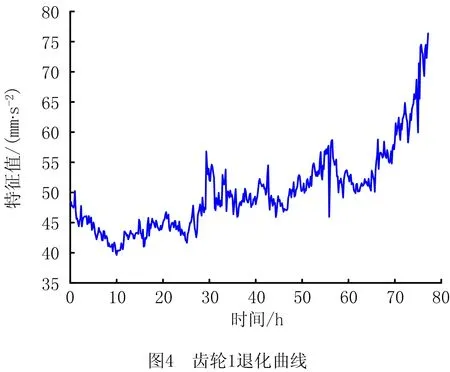
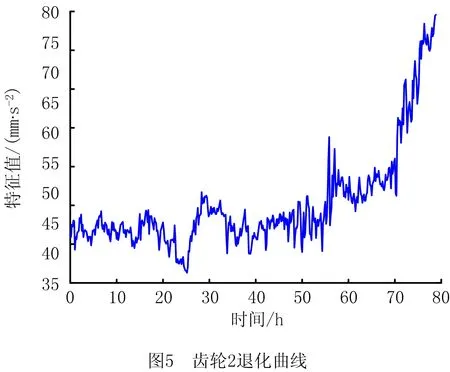
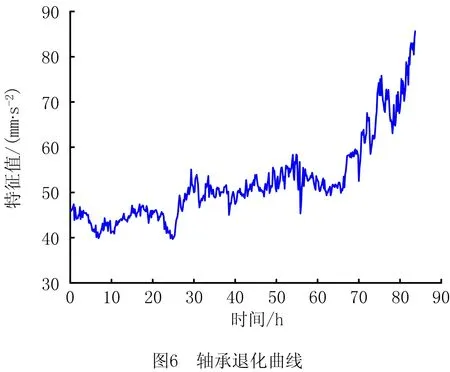
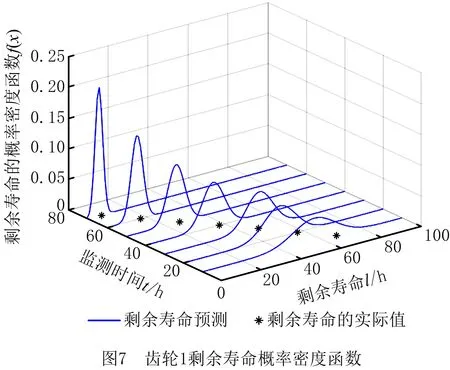
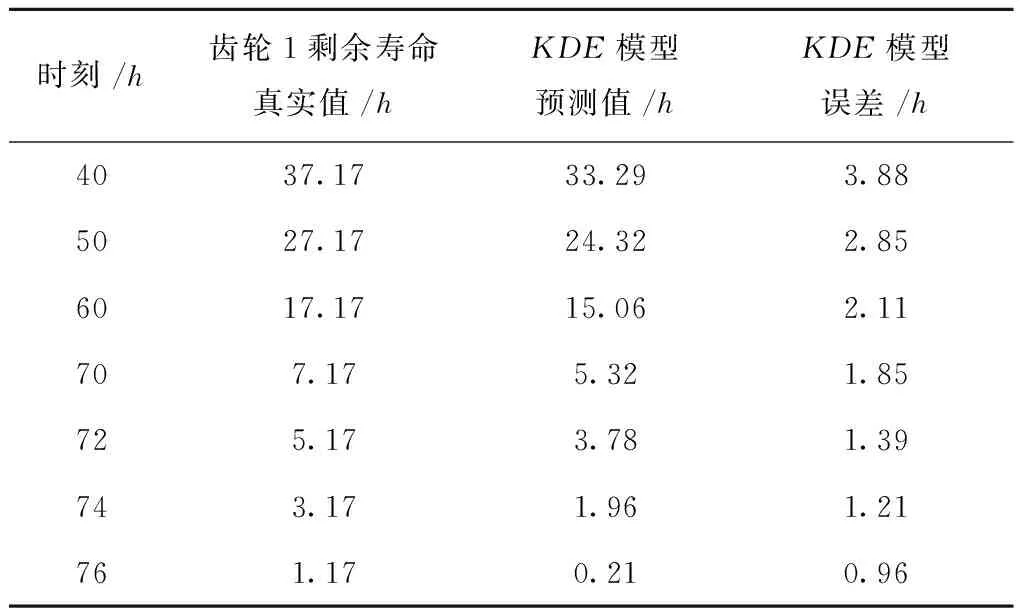
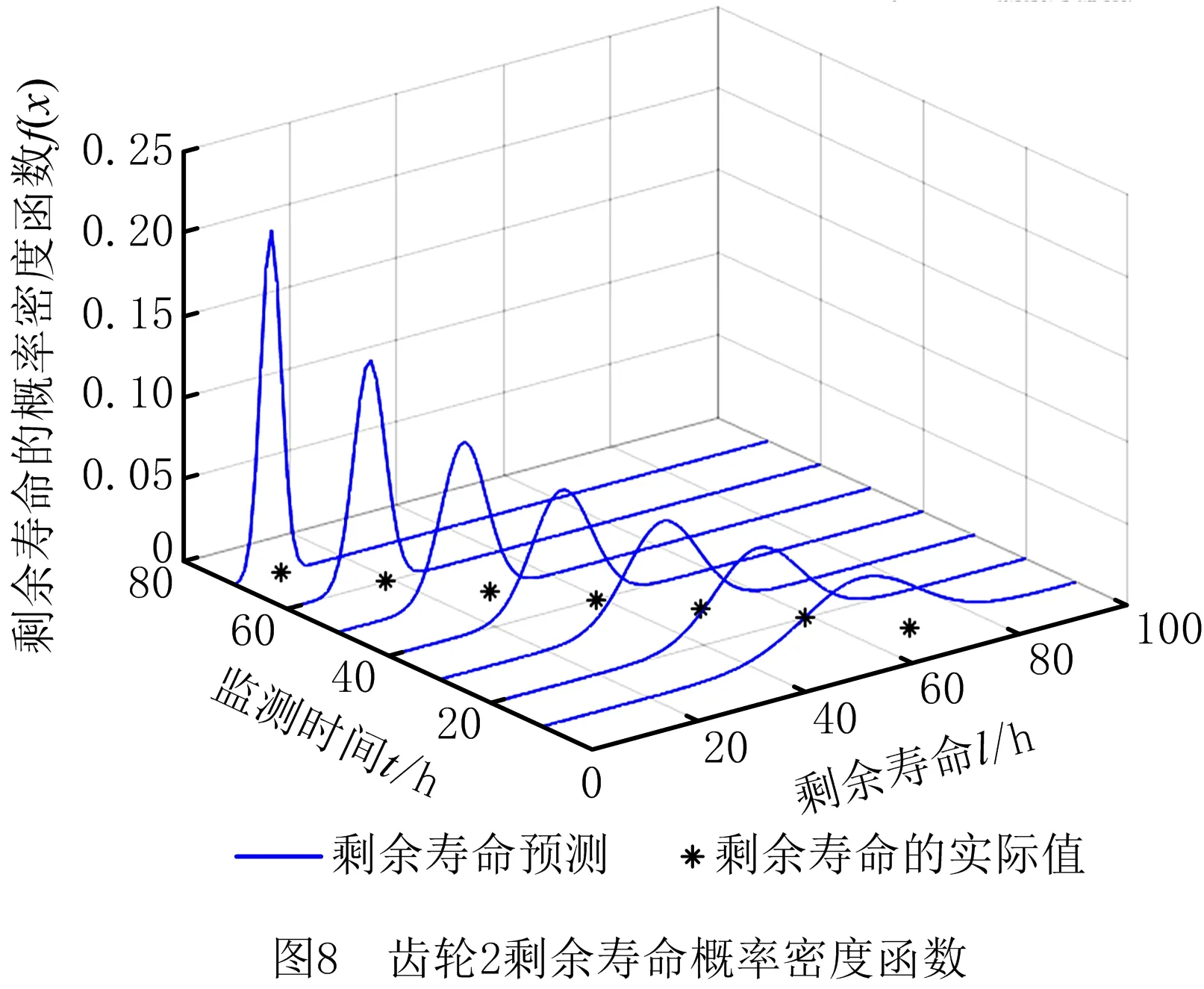
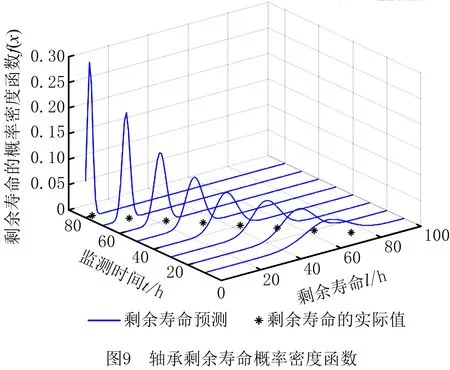
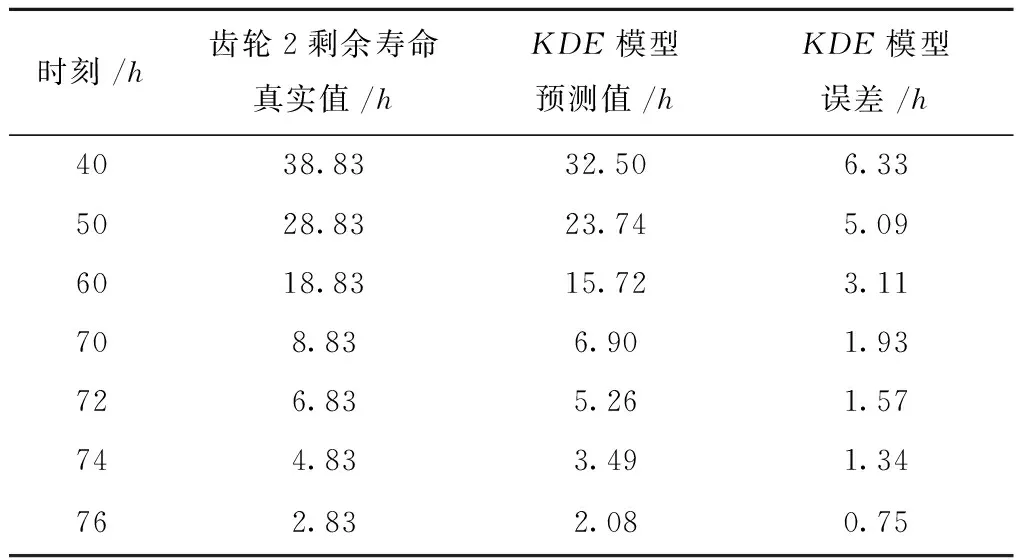
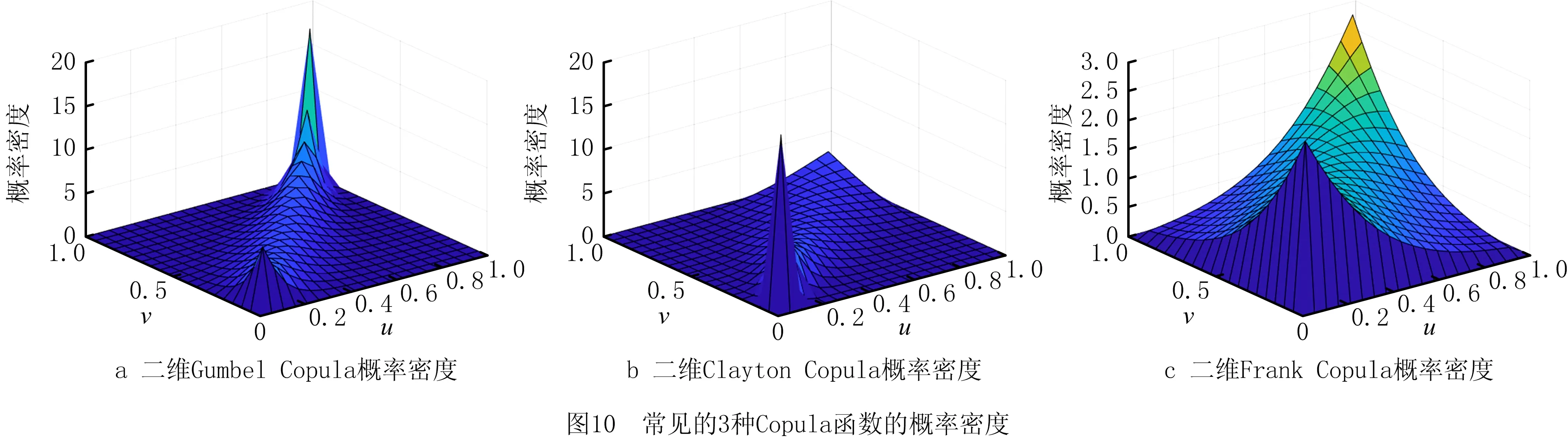
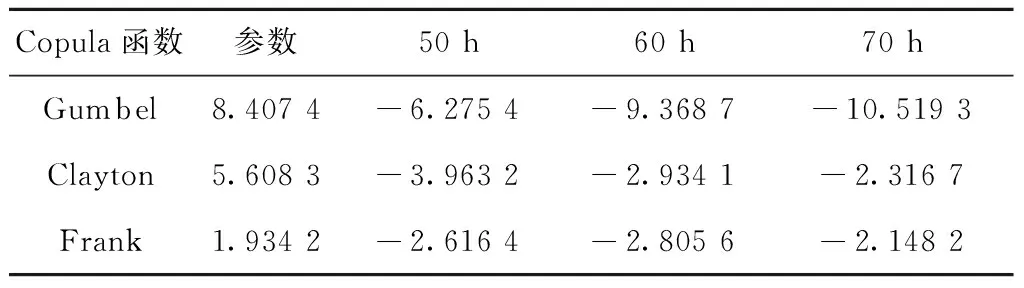
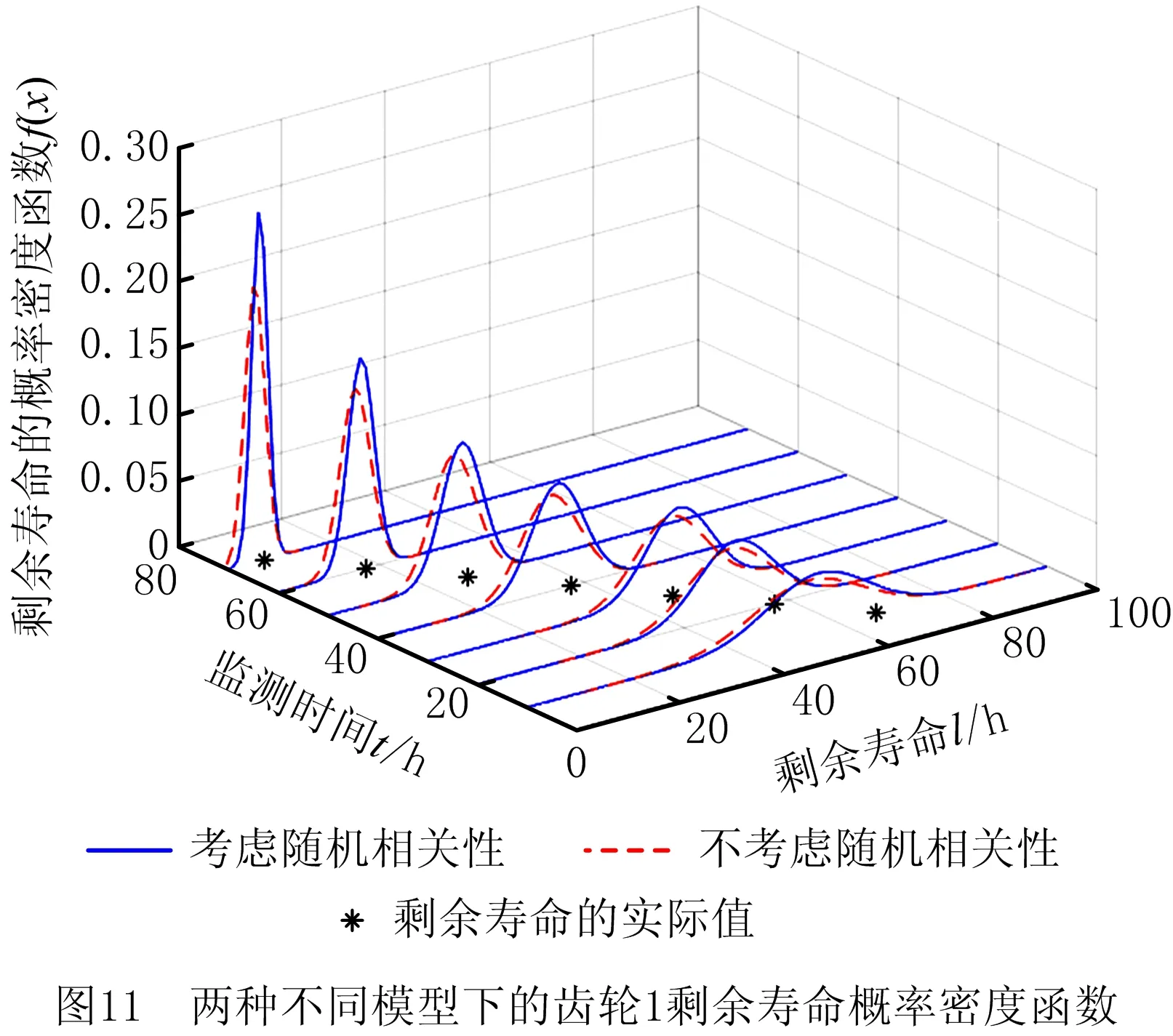
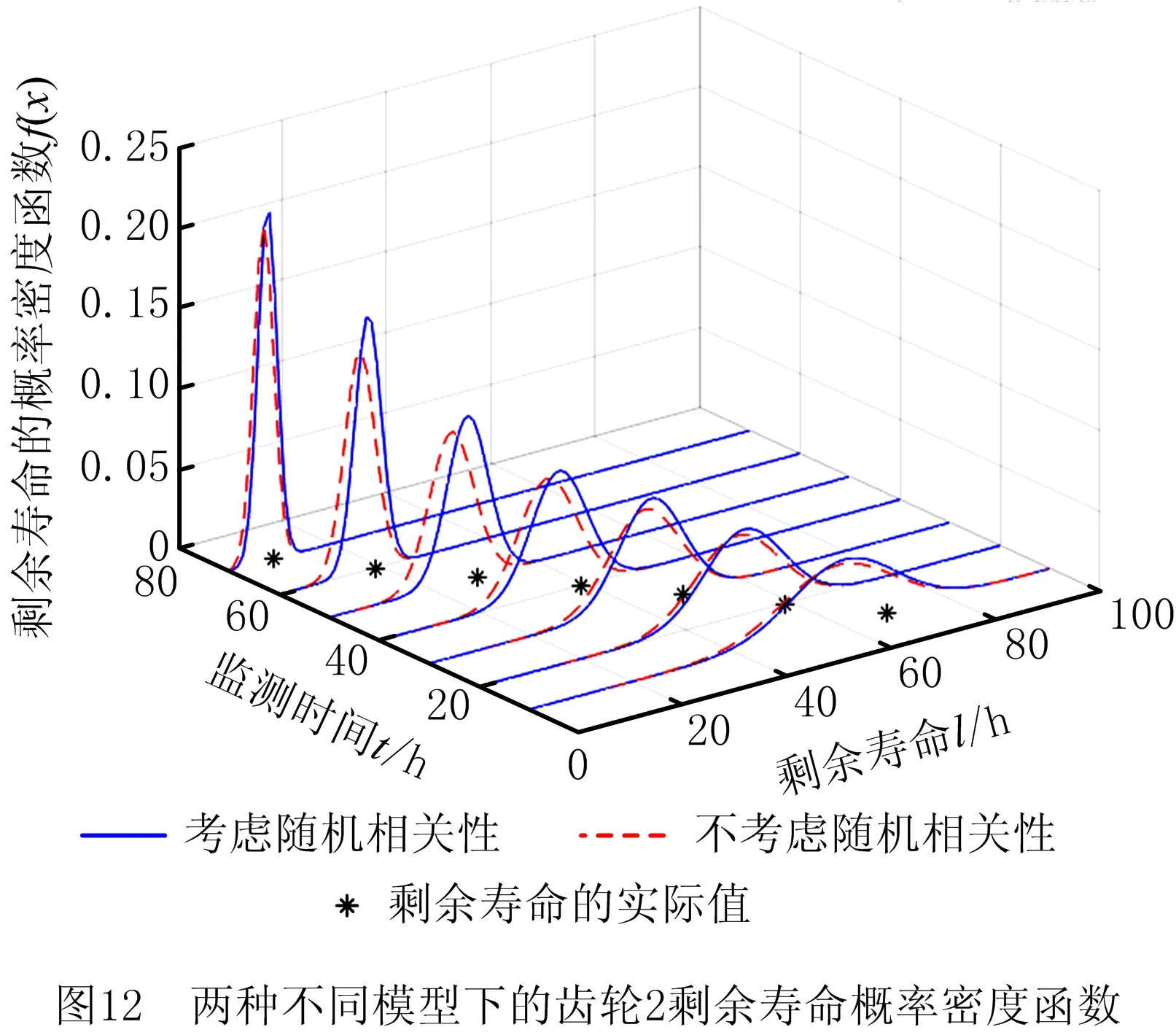
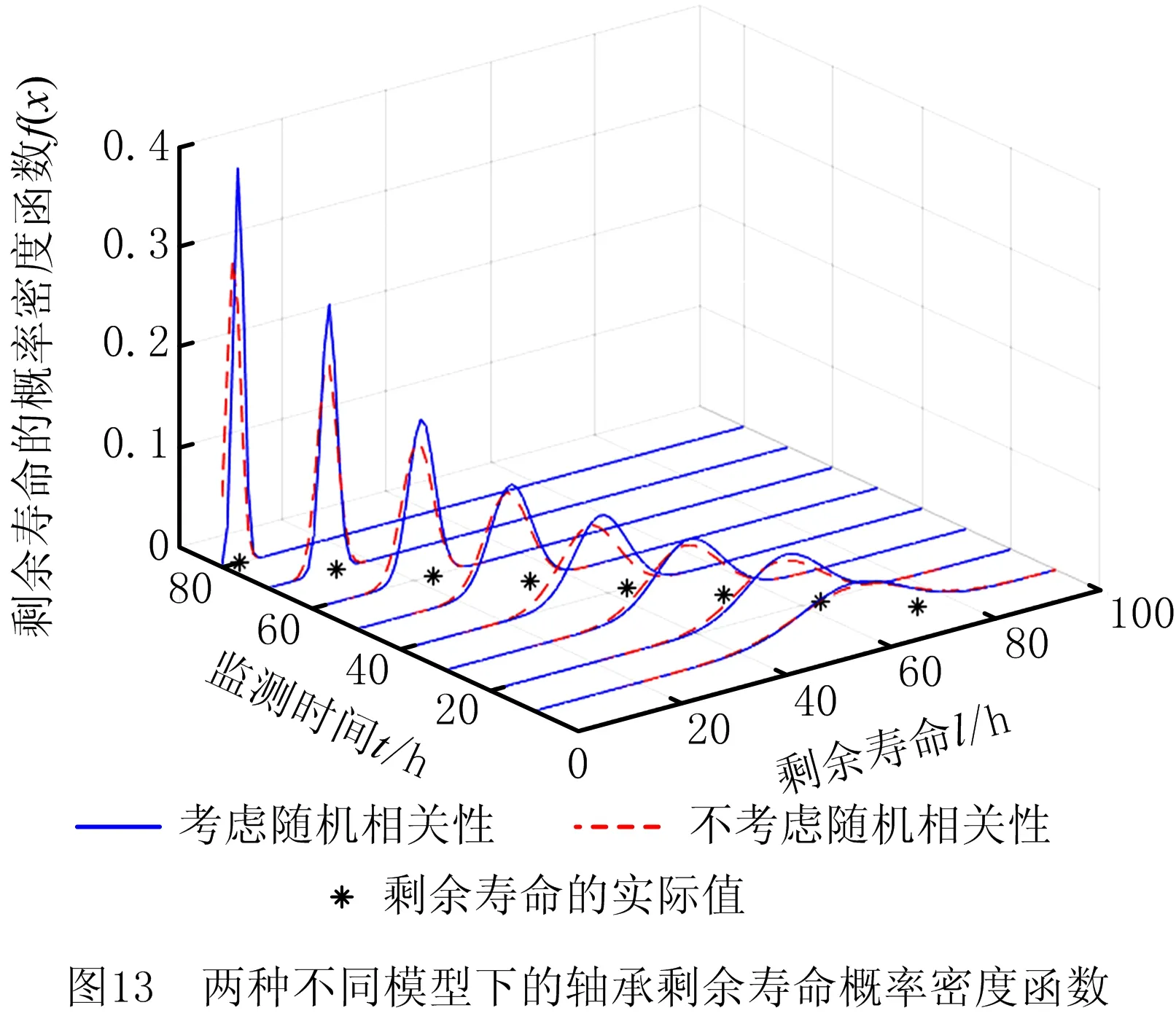
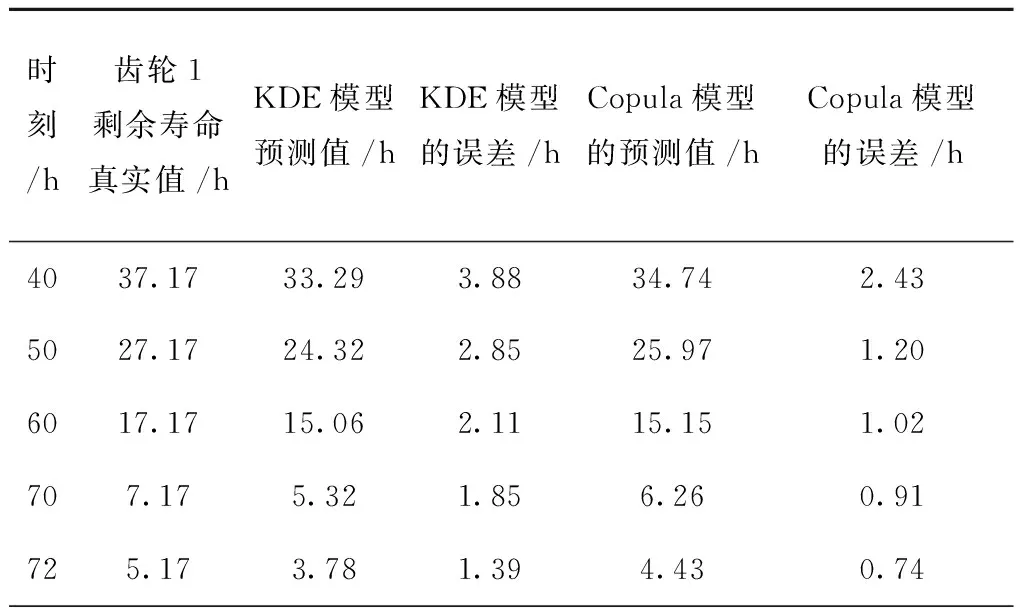
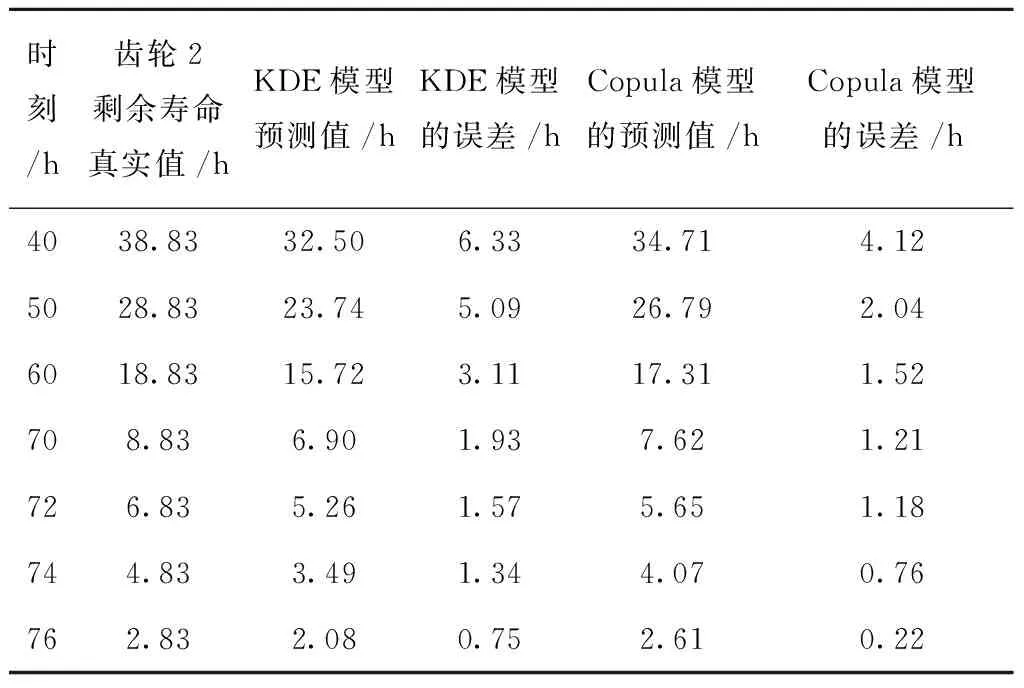
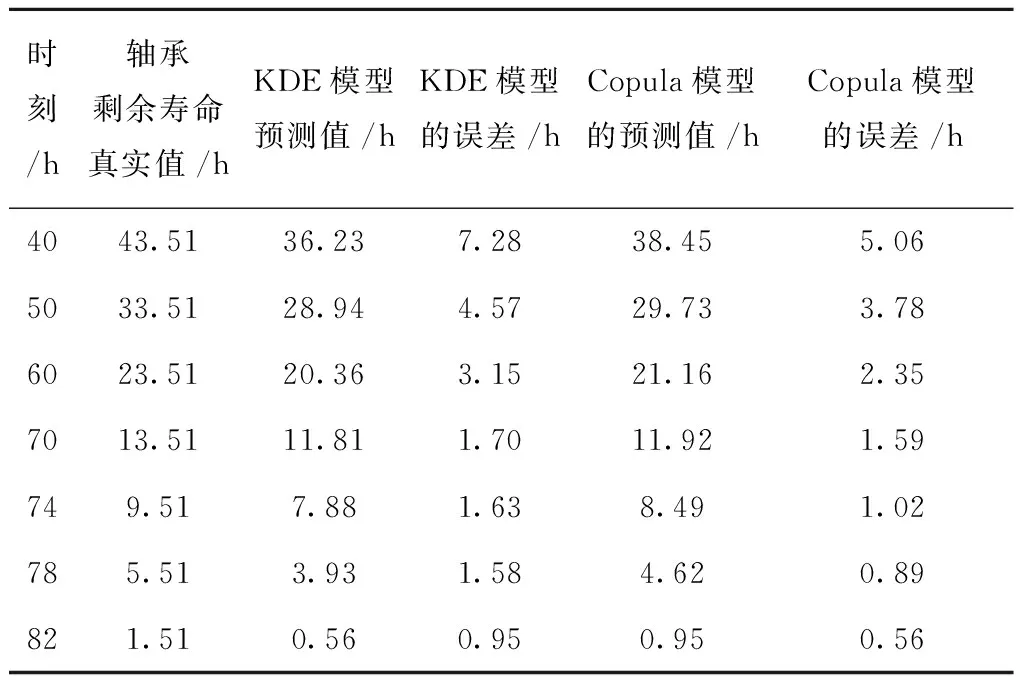
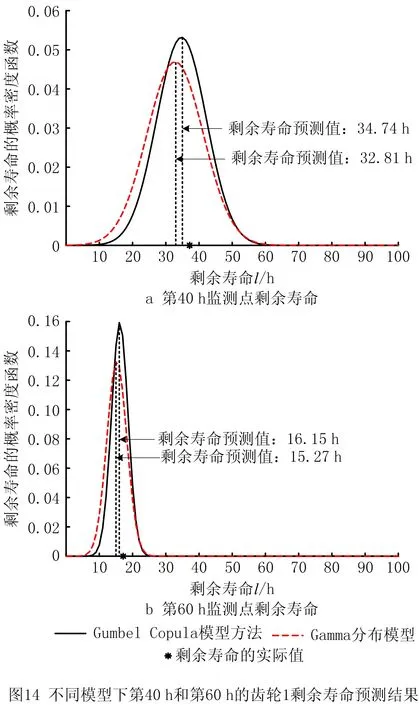
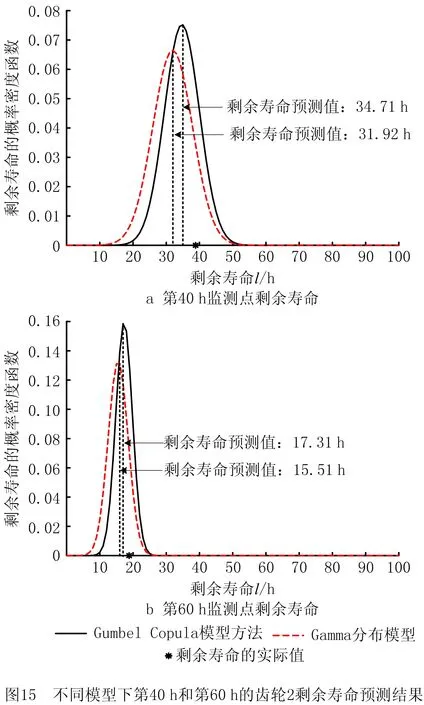
0 (11) 其中: 采用Kendall秩相关系数τ判断其部件间存在相关性后可通过Copula函数表征其相关关系。 假设系统中M个部件存在随机相关性,其剩余寿命联合分布函数F(t1,t2,…,tM)为M维分布函数,可用Copula函数表示为: F(t1,t2,…,tM)=C(F1(t1),F2(t2),…,FM(tM);θ)= C(u1,u2,…,uM;θ)。 (12) 式中θ为相关参数,用来表征相关性程度。 根据SKlar定理可知,选择合适的Copula函数C就可以通过Copula函数得到退化分布函数的联合分布函数。将部件的剩余寿命的退化分布函数式(8)带入式(12)中得: (13) (14) (15) 第i个部件在考虑随机相关性下的条件分布函数为: (16) (17) (18) 表1中列举了几种常见的Copula函数形式。 表1 常见的Copula函数 在实际应用中,Copula函数的种类很多,如表1所示为3种常用的Copula函数形式,选择不同的Copula函数进行研究,可能会导致不同的分析结果。赤池信息准则(Akaike Information Criterion, AIC)、贝叶斯信息准则(Bayesian Information Criterion, BIC)和交叉验证法(Cross-Validation, CV)是统计学中模型选择和评价的重要工具。WEI等[34]通过实验验证了AIC和BIC比CV准则的计算速度更快,AIC准则可用于衡量估计模型的复杂度与退化数据拟合程度[9,29],且能更好地避免参数过拟合,因此采用AIC准则来检验函数拟合的优劣性,AIC值越小表明模型越适合。 通过AIC准则选择最优的Copula函数,AIC表达式为: (19) 式中:n为样本个数,P和Q分别表示Copula函数的似然函数值和参数个数。 对于Copula函数中的未知参数θ,本文采用极大似然函数进行估计。首先利用非参数核密度估计得到退化分布函数,然后利用极大似然估计方法估计Copula函数中的未知参数θ。 (20) 通过式(20)求得不同Copula函数的参数θ及其似然函数值,将其似然函数值代入式(19)分别计算对应的AIC。选择AIC值最小的Copula函数代入式(13),通过式(13)~式(18)即可求解考虑随机相关性的部件剩余寿命概率密度函数。 如图1所示为本次试验所用的齿轮箱试验台,由主试齿轮箱和陪试齿轮箱相连接构成,其中心距为150cm,试验采用机械杠杆加载,扭矩采用转矩转速传感器测量,试验过程中对主、陪试箱体的振动、加速度、温度及噪声进行监测,主试齿轮箱中为正反交错搭接的一对齿轮,齿轮的断齿等效为齿轮的失效,轴承的外圈磨损等效为轴承的失效。 试验台架上共布置13个传感器,传感器安装情况如图2所示,1#、2#、3#、4#加速度传感器分别布置在主试箱内轴承座的径向位,7#、8#加速度传感器分别布置在主试箱内轴承座的轴向位,5#、6#加速度传感器分别布置在陪试箱内轴承座的径向位;9#、10#声音传感器分别悬挂在主试箱和陪试箱正上方40cm处;11#温度传感器布置在主试齿轮箱内部;12#转速传感器布置在驱动电机的输出端;13#转矩传感器布置在主、陪试箱的联接轴处。主试箱齿轮啮合情况如图3所示。 试验中加载分八级载荷,八级载荷的大小分别为349.5扭矩,430.7扭矩,492.2扭矩,555.6扭矩,612.9扭矩,693.4扭矩,734扭矩,822.7扭矩,前七级载荷的运行时间均为10个小时,在第八级载荷时监测到各部件发生故障,剩余寿命预测选取从第八级加载开始后的加速度数据进行分析。由图2可知,4#和1#加速度传感器的位置最靠近主试箱的齿轮,8#加速度传感器的位置最靠近主试箱的轴承,因此将4#、1#和8#加速度传感器的振动信号分别作为齿轮1、齿轮2和轴承的退化信号。其采样频率为25.6kHz,每次采样持续60s,每隔9min记录一次采样数据。 齿轮箱的退化轨迹整体呈上升趋势,为了更好地反映各部件的退化趋势,采用均方幅值方法对数据进行特征提取,可由下式计算: (21) 式中:Ni为采样点数,yj为振动信号幅值。 通过均方幅值法对齿轮箱齿轮1、齿轮2和轴承的数据进行处理后,得到如图4~图6所示的退化曲线图。可以看出,齿轮1在发生故障时的故障阈值为L1=76.375mm/s2,齿轮2在发生故障时的故障阈值为L2=79.580mm/s2,轴承在发生故障时的故障阈值为L3=85.637mm/s2。齿轮1的真实寿命为77.17h,齿轮2的真实寿命为78.83h,轴承的真实寿命为83.51h。 利用齿轮箱所提取的特征值来验证不考虑随机相关性的齿轮1剩余寿命预测KDE模型。由式(10)可求得齿轮1的剩余寿命概率密度函数,图7给出了不同监测时刻齿轮1的剩余寿命预测结果。从图中可以看出,从监测的10h~70h,剩余寿命概率密度图的方差逐渐减小,这是由于在监测初期的数据量少,随着数据的增多,预测结果也越准确。 如表2所示为齿轮1对KDE模型的预测结果误差分析。 表2 齿轮1剩余寿命的预测结果与实际值的误差分析 表2给出了齿轮1在不同监测时刻的预测值、实际值和模型误差值。由表中的数据可知,随着监测时间的增加,数据量增大,该模型所预测的结果与真实值的误差逐渐减小,对齿轮1剩余寿命的预测也更加准确。 同理,用同样的方法来分别验证不考虑随机相关性的齿轮2和轴承的剩余寿命预测KDE模型,可以得到不同监测时刻下齿轮2和轴承的剩余寿命预测结果,如图8和图9所示。 齿轮2和轴承对KDE模型的预测结果误差分析分别如表3和表4所示。 表3 齿轮2剩余寿命的预测结果与实际值的误差分析 表4 轴承剩余寿命的预测结果与实际值的误差分析 齿轮2和轴承的预测结果同样说明,随着监测时间的增加,该模型的预测误差也逐渐减小,说明了基于核密度估计的剩余寿命模型对齿轮2和轴承剩余寿命预测的准确性。 通过式(11)求得齿轮1和齿轮2,齿轮1和轴承,齿轮2和轴承的Kendall秩相关系数τ分别为0.413 8,0.713 5,0.327 3,说明齿轮1,齿轮2和轴承为存在随机相关的多部件系统。 常见的3种Copula函数二维概率密度图如图10所示。 由图10可知,GumbelCopula函数可描述上尾相关关系,ClaytonCopula函数可描述下尾相关关系,FrankCopula适合描述具有对称相关结构的相关关系。由于部件的退化程度越大,对其他部件的影响也越大,部件之间的退化存在尾部相关性,且这种相关性是非对称的,可见使用上尾相关性更适合描述不同部件间的随机相关性。 通过极大似然估计Copula函数的参数,然后根据AIC准则选择最优的Copula函数。由式(19)得到如表5所示的3种常用Copula函数的AIC值。 表5 常用Copula函数的AIC值 由表5可知,在相同的时刻下,AIC值最小的为Gumbel Copula函数,因此根据AIC准则可知最优的Copula函数应选择Gumbel Copula函数,可以更好地描述部件之间的相关性,这与所分析的Gumbel Copula函数特性一致。 将部件的剩余寿命分布函数式(9)和表1中的Gumbel Copula函数表达式代入式(13)中,可求得3部件的联合分布函数为: (22) (23) (24) (25) (26) (27) (28) 用齿轮箱提取的特征值来验证考虑随机相关性的剩余寿命预测模型。可分别求得齿轮1、齿轮2和轴承的剩余寿命预测结果,其在不同监测时刻的预测结果如图11~图13所示。 图11~图13显示了在不同监测时刻下,两种不同模型对齿轮1、齿轮2和轴承的剩余寿命预测结果。从图中可以看出,随着监测时间的增加,两种模型的剩余寿命概率密度函数曲线方差逐渐减小,而且真实值都在两种模型预测的范围之内。同时考虑随机相关的剩余寿命预测模型结果更接近真实值。表6~表8分别对3个部件考虑随机相关性的剩余寿命预测模型和不考虑随机相关性的KDE模型预测结果进行误差分析。 表6 两种模型下齿轮1剩余寿命预测结果误差分析 续表6 表7 两种模型下齿轮2剩余寿命预测结果误差分析 表8 两种模型下轴承剩余寿命预测结果误差分析 对比表中数据可知,随着监测时间的增加,两种模型预测的准确度均在增加。而且在相同监测时刻,基于Copula理论考虑相关性剩余寿命预测结果比KDE剩余寿命预测结果有更小的绝对误差。由此表明,考虑部件之间的随机相关性后,预测齿轮的剩余寿命比不考虑随机相关性所预测的结果更为准确。 为进一步验证本文所提出的模型,使用相同的样本数据采用Gamma分布模型分别对3个部件进行剩余寿命预测,图14~图16分别给出了在第40 h和第60 h的Gumbel Copula模型与Gamma分布模型的预测结果对比图。通过比较可以得出,Gumbel Copula模型方法的预测结果比Gamma分布的预测结果更接近于剩余寿命的真实值。随着监测时间的增加,样本增多,两种模型的精确性也更高,而Gumbel Copula模型的预测误差更小,说明考虑部件随机相关性后可以更准确地对部件的剩余寿命进行预测。 本文考虑连续退化多部件系统中部件间存在的随机相关性,首先基于核密度估计的方法进行退化分布建模;然后利用Kendall秩相关系数进行相关性分析;接着采用Copula函数表征部件退化的相关性,建立相应的剩余寿命预测模型;最后通过试验验证了基于Copula的考虑随机相关性的多部件剩余寿命预测结果比不考虑随机相关性的剩余寿命预测结果更接近剩余寿命的真实值,证实了该方法的有效性。未来将在多部件预测的基础上,建立混合Copula的联合剩余寿命预测方法,进一步提高预测结果的准确性。2.2 考虑随机相关性的多部件剩余寿命预测模型
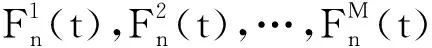
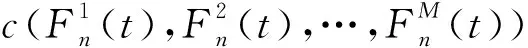
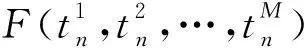

3 试验验证分析
3.1 数据采集


3.2 单部件的剩余寿命预测

3.3 考虑随机相关性的部件剩余寿命预测
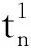
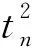
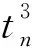

4 结束语

