基于μ-PPT电推进器的立方体卫星群落姿态协同控制

张科文，潘柏松

(1.浙江工业大学 机械工程学院，浙江 杭州 310023；2.浙江工业大学 特种装备制造与先进加工技术教育部重点实验室，浙江 杭州 310023；3.浙江双环传动机械股份有限公司，浙江 台州 317600)

0 引言

微小卫星体积小、重量轻、研制周期短、发射成本低，近年来得到了越来越多的关注。凭借这些优势，微小卫星可以通过组建群落，开展基于多个卫星的协同任务，包括地球科学、太空应用、深空探测以及空间技术验证等[1]。多个微小卫星构成的群落需要群落成员之间能够进行数据交换和协调，因此具有更复杂的网络体系结构。例如，Google、Facebook和SpaceX等多家公司设想利用数百甚至数千颗小卫星来实现全球卫星传输网络，以较低的成本和较少的能耗，进行全球监测、灾难恢复以及物联网等应用[2]。

目前，微电子和微系统技术的发展大大减少了小卫星的质量和功耗，同时提高了小卫星的灵活性和耐用性[3]。这类技术的使用让所有的电子系统都可以嵌入到尺寸为厘米级的构架中，由此产生的一类典型小卫星被称为立方体卫星。立方体卫星是由美国加州理工学院和斯坦福大学于1999年率先提出的，是一种能够在短时间内研制并且用于示教需求的微小卫星[4]。立方体卫星是由一个或多个体积为10×10×10 cm3的立方体单元组成的微小卫星，每个单元体的质量约为1.33 kg[5]。立方体卫星的优势不仅在于其模块化的标准结构，还在于其内部硬件能够从现有市场产品中获得，这使它能够保持较低的制作成本。

目前，大多数与立方体卫星相关的任务是基于单个卫星展开的。例如，FISH等[6]利用单个立方体卫星来分析动态电离层现象，研究造成电离层风暴增强密度凸起形成的物理过程，以及这一过程与穿透电场之间的关系。此外，还有麻省理工学院发起的CommCube小卫星系列任务，测试使用立方体卫星作为数据中继站点的可能性，该中继站能够增加卫星到地面站的通信时间和信息吞吐能力[7]。此外，还有三单元体立方体卫星LituanicaSAT-2，用来进行在轨技术测试，包括测量低热层原子和氧分子的时辨行为，以及测试绿色单推进剂微型推进器对立方体卫星的轨道操纵和阻力补偿能力[8]。

以上任务都是利用单个立方体卫星作为空间平台来开展科学探索和技术测试。然而，多个立方体卫星的协同合作更能发挥出它们的优势。立方体卫星群落的部署使整体对内部组件故障具有很高的容错率，能够适用于更多不同的应用场景。例如，文献[9-10]描述了由50个立方体卫星组成的月球轨道分布式低频天线组网系统，该系统具有很高的可扩展性，能够用于对宇宙背景辐射进行数据采样与处理。文献[11]描述的风暴和热带系统实验任务，利用在地球轨道上等距分布的5个立方体卫星，来确保每个立方体卫星每隔一段时间通过同一观测点，从而可以在短时间内观测大气云活动，相比传统卫星监视大气云的时间间隔要短得多。多个立方体卫星构成的微小卫星群落灵活性高、鲁棒性强，能够发挥出单个普通卫星没有的功能优势。目前，基于多个立方体卫星群落执行的复杂任务，主要包括空间数据处理和传输以及天文观测等，特别是在遥感领域的应用已越来越多。

立方体卫星通过群落这种网络体系结构，能够共享可用资源，使效益最大化。为保证立方体卫星群落能够有效地执行群体协同任务,需要对群落中的个体具有较好的协调控制能力。针对立方体卫星特殊构造和自身性能限制，建立适用于立方体卫星群落姿态同步模型，并设计相应的控制策略是保证微小卫星群落空间任务高效有序执行的关键。

立方体卫星中的姿态控制系统根据任务需求能够实现姿态的维持和调整。由于其结构局限性，需要配置小尺寸高性能的微型推进器系统。其中，微脉冲等离子推进器体积小、结构简单，能够通过加速等离子体产生推力[12]。μ-PPT电推进器的优势在于能够通过控制脉冲冲量进行精确操作，并且能够满足任务需要的鲁棒性[13-14]。

为了探究由多单元立方体卫星组成的微小卫星群落姿态协同性能，本文利用立方体卫星配置的姿态控制模块，来分析和论证实现微小卫星群落姿态同步需求的可行性。其中，构成群落的N个立方体卫星可以有不同的模块结构和质量。通过群落内部通信交换各自状态信息，立方体卫星群落能够利用设计的自适应控制策略实现姿态同步的自适应调节。然后，再通过群落中每个成员配置的脉冲推进模块实现实时姿态调整。最后，通过两个不同的立方体卫星群落姿态同步案例的仿真分析，验证了提出的自适应控制策略与离散μ-PPT电推进系统能有效地实现立方体卫星群落姿态协同控制任务需求。

1 立方体卫星群落姿态同步模型

1.1 姿态动力学

考虑一个由N个立方体卫星组成的微小卫星群落，为了实现整个群落的姿态同步，首先对每个立方体卫星进行姿态动力学描述。利用欧拉转动方程来表示立方体卫星的姿态动力学模型[15]：

(1)

式中：下标i=1,…,N分别指代群落中的每个立方体卫星；Ji∈R3×3是惯性矩阵；ωi是角速度矢量；τi是控制力矩；τd,i是外部扰动力矩。同时，这里考虑的微小卫星群落中的成员可以是不同类型的立方体卫星，可以有不同的尺寸和质量。

为了将上述方程转化为更适合于参数化的系统模型表达式，引入修正的罗德里格参数(Modified Rodrigues Parameters, MRP)建立群落中立方体卫星的姿态动力学模型[15-16]。此时，MRP姿态矢量qi=[qi1;qi2;qi3]与角速度矢量ωi的关系式可表述为:

(2)

式中:

其中，反对称矩阵S(qi)定义为:

结合式(1)和式(2)，可以得到群落中的每个立方体卫星姿态动力学模型的欧拉—拉格朗日表达式，即

(3)

式中:

Mi(qi)=Z-T(qi)·Ji·Z-1(qi)；

Z-1(qi)-Z-T(qi)·S(Jiωi)·Z-1(qi)；Ti=Z-T(qi)·τi；Td,i=Z-T(qi)·τd,i。

上述欧拉—拉格朗日动力学模型式(3)满足以下基本性质[17-18]：

(1)惯性矩阵Mi具有上下界，即

0<λmin{Mi}·I3≤Mi≤λmax{Mi}·I3<∞。

其中λmin{Mi}和λmax{Mi}分别表示矩阵Mi的最小和最大特征值。

(2)任意矢量x∈R3满足以下关系式，即

其中k>0。

1.2 立方体卫星信息交互网络

假设群落中的立方体卫星通过搭载的通信设备能够实现群落成员的信息交流，采用图论方法[19]可以描绘群落中每个立方体卫星之间的信息互联的网络结构关系。如图1所示，群落信息网络关系图是由若干给定的顶点以及连接两个顶点的边所构成的图形，并且被定义为G∈(V,E)，其中：V={v1,v2,…,vn}是图形G中顶点的集合，顶点vi代表了群落中每个立方体卫星；E⊆V×V是图形G中边的集合，代表了立方体卫星之间的信息互联关系。

为了描述某个立方体卫星与其他小卫星的信息交互情况，引入邻接矩阵A(G)，即：若边(vivj)∈E，表示两个小卫星vi和vj之间有信息交互，对应的邻接矩阵元素[A(G)]ij=1；否则，对应元素[A(G)]ij=0。此外，引入度数矩阵D(G)来表示图形中与某个顶点vi邻接的其他顶点的个数。由邻接矩阵和度数矩阵能够得到图形G的拉普拉斯矩阵L(G)，即L(G)=D(G)-A(G)。这里两个立方体卫星邻接表示它们能够进行通信，与其空间位置无关。

此外，若图形G中顶点与顶点之间的通信是有方向性的，称为有向图(如图1b)。有向图中的边具有指向性，例如边(vivj)∈E表示信息从顶点vi流向了顶点vj。

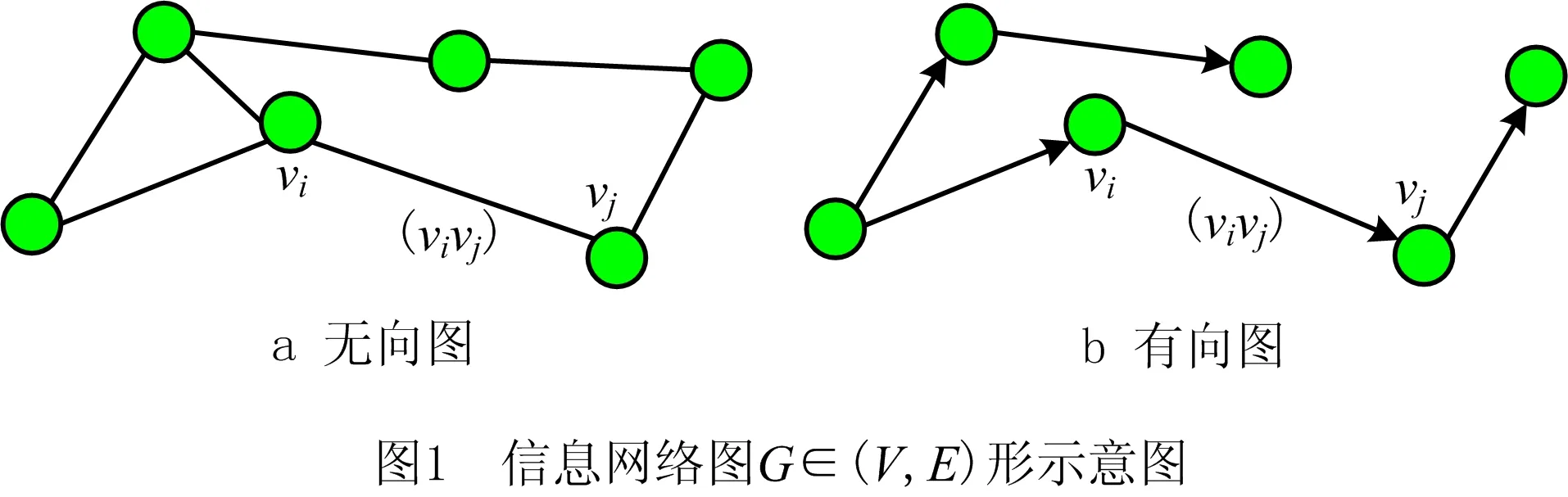
若图形G囊括群落中的全部顶点，并且保证信息在群落内部能够流通，则称图形G包含一个生成树。无论是无向图还是有向图，假设其拥有一个生成树。这种情况下，拉普拉斯矩阵L(G)有一个特征值为0，其余的特征值的实部均为正数[20]。在微小卫星群落中引入图论表述能够从数学模型角度分析与表达立方体卫星的状态信息交互方式。

1.3 立方体卫星配置

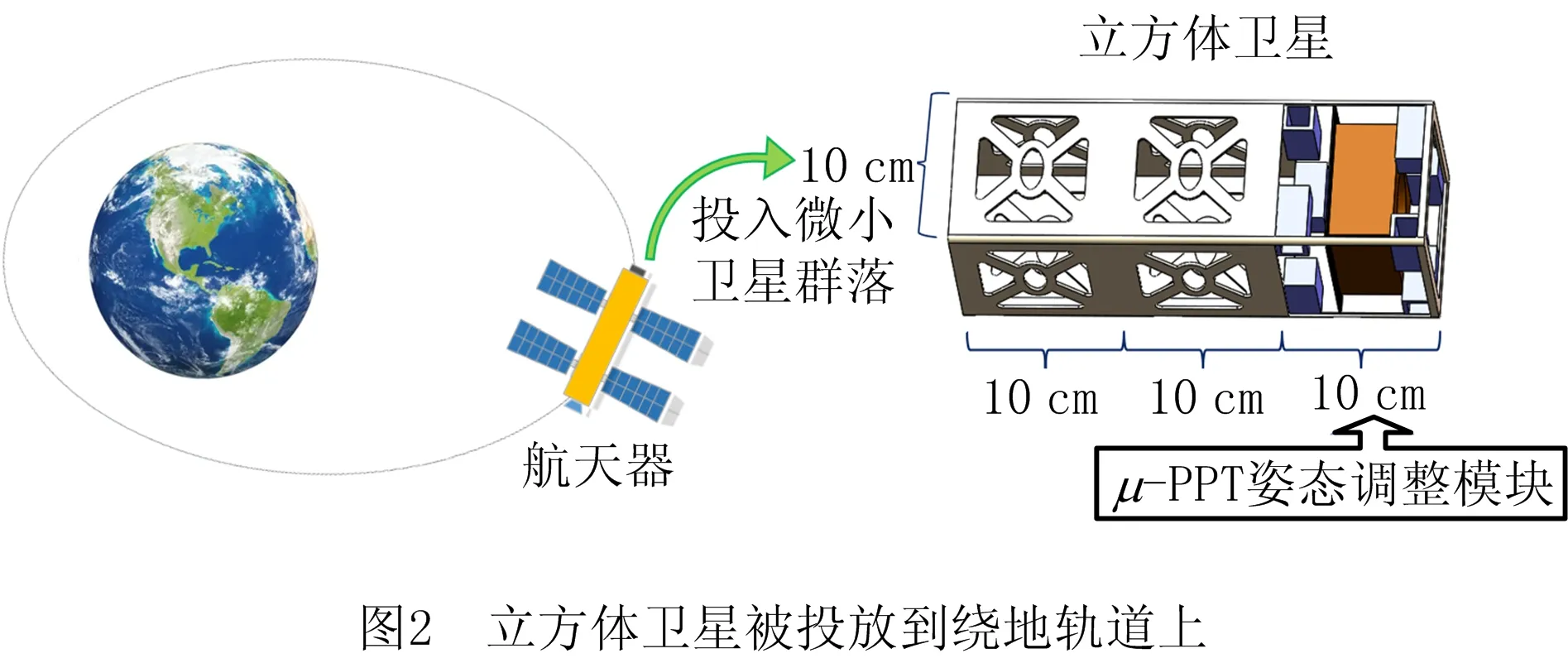
立方体卫星一般由大型航天器通过微小卫星轨道部署器投放到目标轨道上。考虑图2所示的标准模块化的三单元立方体卫星，其姿态调整模块单元由8个μ-PPT推进器组成。每个μ-PPT推进器包含一个微型火花点火器，能够在每个放电周期内启动一次放电。在这极短的放电时间内，由推进剂电离形成的等离子体在电磁力作用下加速产生推力。该推力形成的扭矩能够使立方体卫星的姿态产生变化。如图2所示的立方体卫星姿态调整模块中的推进器系统由上下两层分别4个μ-PPT排列组成，能够为立方体卫星提供三轴姿态控制。

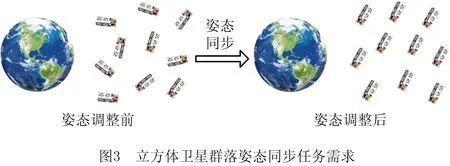
基于立方体卫星能耗低、容错率高的优点，考虑图3所示的由多个立方体卫星组成的微小卫星群落。由于微小卫星轨道部署器的随机投放，群落中的每个立方体卫星有着不同的初始姿态。此外，允许组成群落的立方体卫星有不同的模块组成和质量。许多由群落执行的空间任务需要每个小卫星保持姿态同步的状态，下面对立方体卫星群落姿态同步问题进行分析与控制设计。

2 立方体卫星群落姿态协同策略

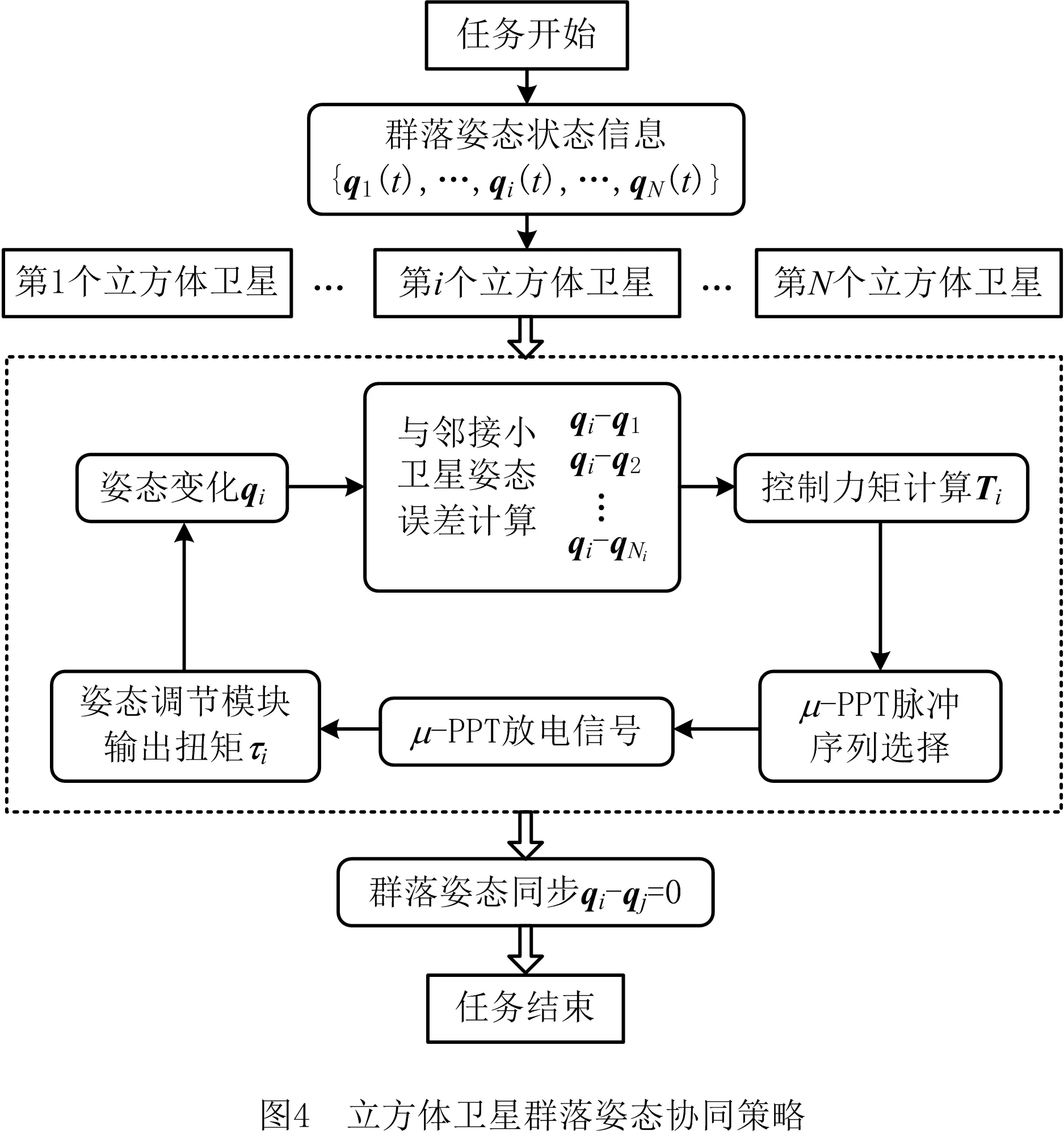
为了实现立方体卫星群落的整体姿态协同这一任务需求，提出如图4所示的姿态同步控制策略。对于群落中的每个立方体卫星来说，基于当前时刻的姿态信息以及接收的邻接小卫星的姿态信息，通过比较实时状态差异，将得到的误差信息用于力矩控制算法中，计算所需转矩Ti。由于μ-PPT特殊的脉冲工作模式，推进器无法输出理论转矩Ti，需要通过选择μ-PPT脉冲序列来确定姿态调整模块内对应的推进器放电组合，使得实际输出的转矩τi最符合Ti。然后，通过选定的μ-PPT实现对当前立方体卫星的姿态改变，直至实现群落整体姿态同步的目标。

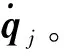
(4)

式中：i=1,…,N，j∈Ni。其中Ni是指与第i个立方体卫星邻接的所有小卫星集合。

考虑到各个邻接立方体卫星的差异性，提出具有同步增益的自适应控制策略。根据立方体卫星与其邻接小卫星之间的每一对初始状态差异，调整图形节点之间的互连增益强度。通过对每个立方体卫星设计控制输入Ti，实现对整个群落的姿态调节的同步性。

首先，针对第i个立方体卫星，定义同步信号变量si(t)如下：

(5)

式中λij>0为同步增益强度系数。根据邻接立方体卫星之间的初始姿态误差选取如下：

λij=ηij·‖qi(0)-qj(0)‖。

(6)

式中ηij>0，‖·‖是欧氏距离。将同步信号变量si(t)代入式(3)，群落中每一个立方体卫星的姿态动力学系统可重新构建为：

(7)

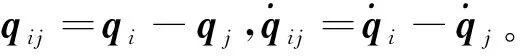
(8)

式中Γi是正定矩阵。基于上述自适应控制律，式(7)变为：

(9)

为了实现立方体卫星群落姿态同步控制目标，考虑闭环系统式(9)，其中同步信号变量由式(5)给出，使用自适应控制律式(7)能够实现同步信号的最终收敛。通过群落信息交互网络以及闭环系统的收敛性，群落中每个立方体卫星的姿态控制目标式(4)能够得到满足。并且，对于群落中每个立方体卫星，基于式(9)构建的系统稳定性和收敛性可以通过如下Lyapunov稳定性分析方法来证明。

证明对基于式(9)的系统进行姿态稳定性与收敛性分析，首先构建如下Lyapunov函数：

(10)

式中i=1,…,N。基于性质(1)的描述，根据惯性矩阵Mi的有界性可知Vi(t)>0且有界。然后，对Vi(t)求导可得

在上式中代入自适应控制律式(8)得到

(11)

进一步求导得出：

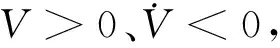
Lw(G)=Dw(G)-Aw(G)。

(12)

式中矩阵Dw的元素dij满足：

矩阵Aw的元素aij满足：aij=λij。然后，基于式(5)定义的第i个立方体卫星的同步信号si，得出群落整体同步信号表达式，即

(13)

3 立方体卫星推进系统姿态调整实现

立方体卫星的姿态调整模块所配置的μ-PPT电推进器在每次极短的脉冲周期内能够产生一个扭矩，用来实现空间3个方向上的角度和角速度控制。基于姿态动力学模型式(1)，在Δt时间内第i个立方体卫星对应的角速度变化量Δωi为：

(14)

其中立方体卫星实际产生的力矩τi由配置的多个μ-PPT推进器产生的合力矩提供。

假设群落中第i个立方体卫星的姿态调整模块中的第k个μ-PPT推进器能够产生的推力为fp,ik，则对应产生的力矩为

(15)

式中：rp,ik为fp,ik到立方体卫星质心的位置矢量；Ibit为脉冲冲量；tp为脉冲持续时间；np,ik为推力单位方向矢量。然后，相应的由m个μ-PPT产生的合力矩为：

(16)

由于μ-PPT特有的脉冲属性，立方体卫星实际产生的力矩τp,i无法完全满足由式(8)给出的理论所需扭矩Ti。因此，需要从配置的μ-PPT中选择一组脉冲序列，使得该序列产生的合力矩与理论扭矩的差异最小。根据模块中每个μ-PPT的布局位置，选择的最优脉冲序列组合能够使τp,i与Ti之间的矢量夹角最小，即

(17)

式中αop,i为最小夹角。由此得到的最优序列组合对应的μ-PPT推进器个数定义为mop,i。在配置的推进器中，这mop,i个μ-PPT输出的最优力矩τop,i为：

(18)

立方体卫星根据上式实际输出力矩τop,i，在一个脉冲周期内能够获得的角速度增量为δωi，即

(19)

由上述分析可知，群落中的每一个立方体卫星配置的姿态控制模块，根据实时群落同步姿态误差，基于控制系统计算得到的自适应控制律式(8)和最优脉冲序列组合，在每个脉冲周期内通过式(18)和式(19)不断改变群落中各个立方体卫星的转动状态，最终能够实现式(4)表述的小卫星群落姿态同步控制目标。

4 微小卫星群落姿态同步案例分析

考虑一个由立方体卫星组成的微小卫星群落，利用提出的控制策略以及配置的推进器系统模块来实现微小卫星群落姿态同步调整。假设群落中有6个不同类型的立方体卫星，每个立方体卫星配置的μ-PPT脉冲冲量为40 μN·s，脉冲频率为1 Hz。表1列出了它们的惯性矩阵数值。

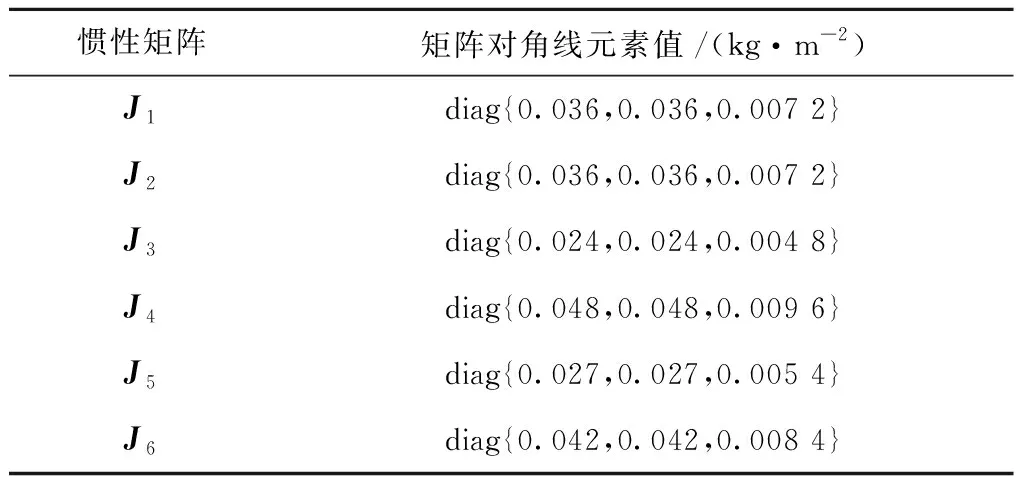
表1 立方体卫星惯性矩阵

表2列出了这6个立方体卫星的初始条件信息。其中，α,β,γ为3个姿态方向角度数值，q1,q2,q3为对应的MRP姿态数值。

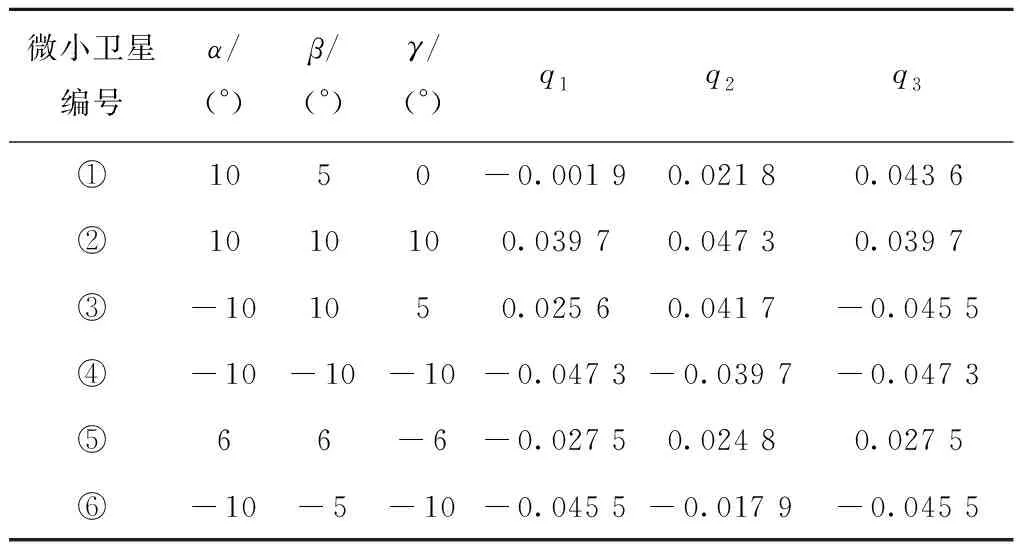
表2 立方体卫星初始姿态角信息

4.1 群落信息无向交互分析

首先，假设群落中6个立方体卫星能够进行双向信息交互，即群落信息交互无指向性。如图5所示绘制的通信图G∈(V,E)为无向图。从群落的无向图中可以看出，邻接立方体卫星之间能够进行双向通讯，即：立方体卫星1与立方体卫星2能够信息互通，2能够与3信息互通，2能够与5信息互通，5能够与4信息互通，6能够与1信息互通。因此，立方体卫星群落通信网络图形G中顶点的集合为V={v1,v2,v3,v4,v5,v6}，图形中边的集合为E={(v1v2),(v2v3),(v2v5),(v5v4),(v1v6)}。

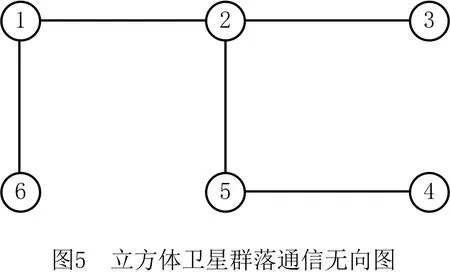
为了验证群落姿态同步效果，提出如下检验标准。首先，计算N个立方体卫星3个方向角的平均数值，即

(20)

通过仿真求得每个立方体卫星与平均值的误差，来验证姿态同步的控制效果，即

Errori=[errori1,errori2,errori3]T=

[αi,βi,γi]T-mean。

(21)

式中i=1,…,N。图5所示的群落中选取N=6，下面给出第1个案例的仿真结果。其中，选择控制器参数ηij=1.5，Γi=diag{1,1,1}，i=1,…,6。表3给出了6个立方体卫星的姿态控制模块中各自配置的8个μ-PPT推进器的脉冲数目。图6分别给出了群落中6个立方体卫星的姿态方向角的仿真结果。结果表明，在提出的姿态同步控制策略以及μ-PPT脉冲推进器执行下，6个立方体卫星由初始不同的姿态角最终趋于同步姿态角度[αmean;βmean;γmean]=[-2.3°;0.72°;-2.6°]。

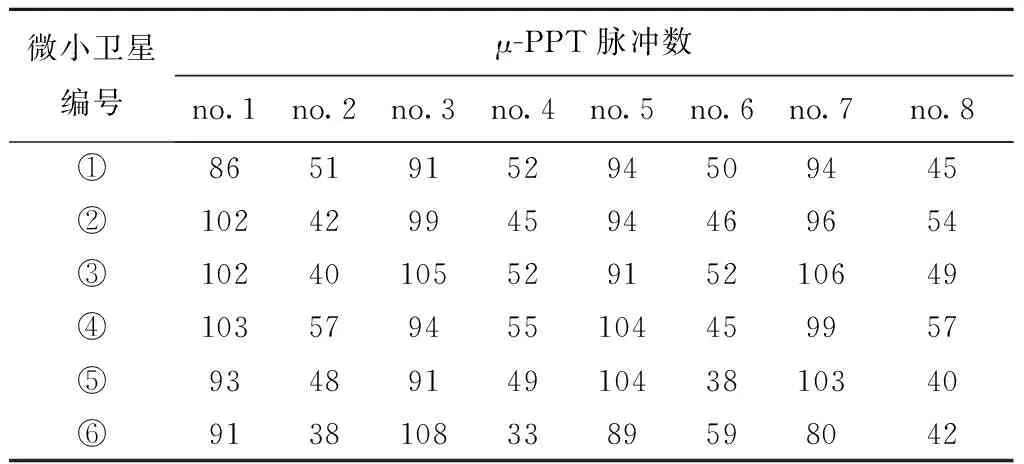
表3 μ-PPT脉冲序列数

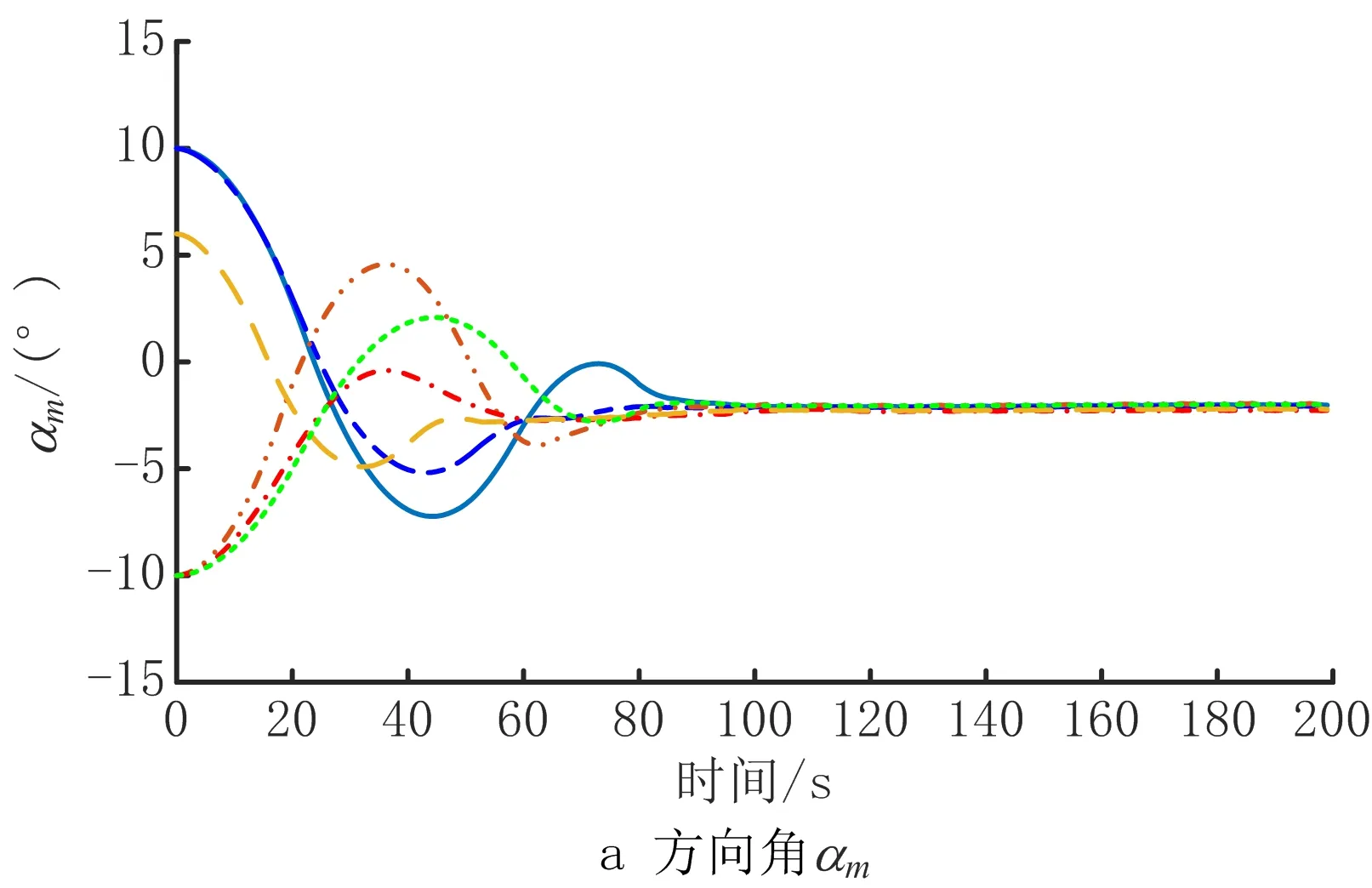
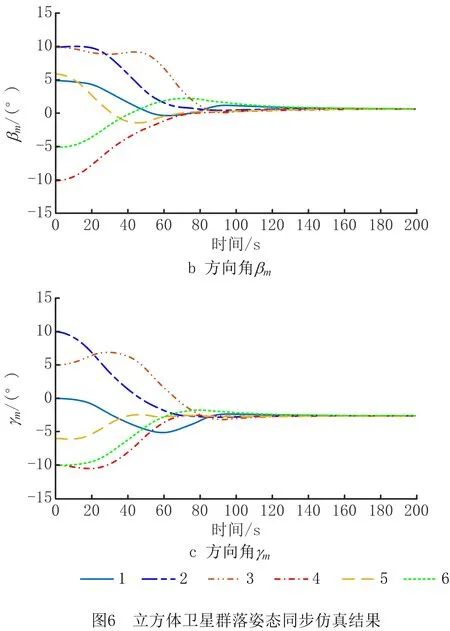
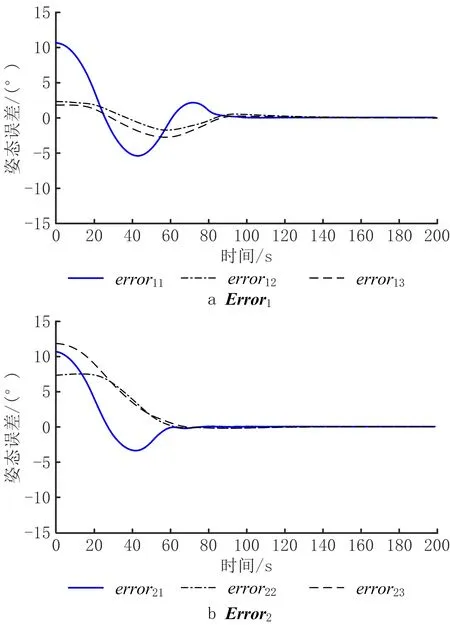
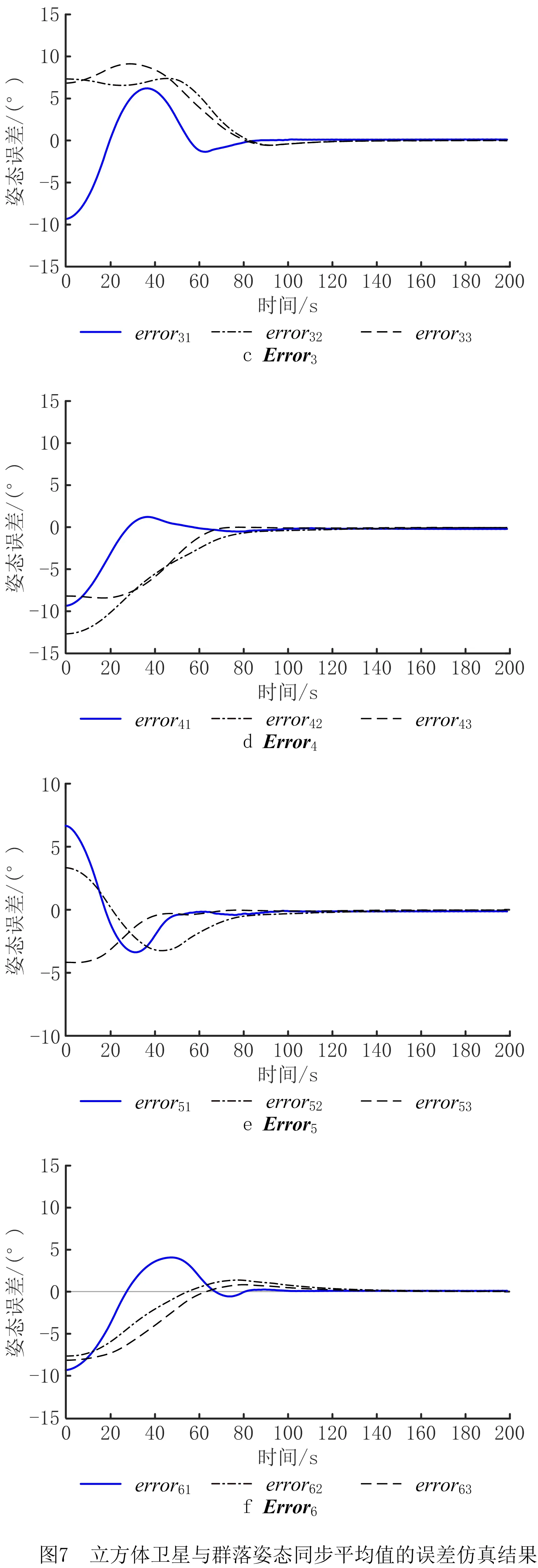
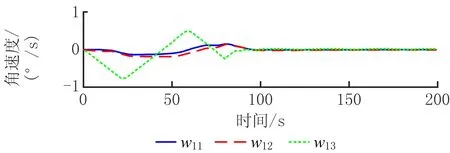
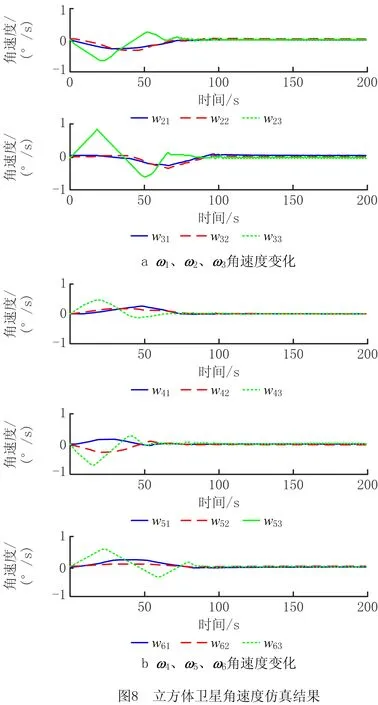
图7所示的仿真结果表明每个立方体卫星与群落整体的姿态同步均值的误差随时间趋于零。图8给出了群落中6个立方体卫星角速度ωi分量随时间演变的仿真结果。结果表明，基于图5所示的立方体卫星群落，每个立方体卫星的姿态同步误差以及角速度最终都趋于零，满足式(4)提出的任务目标。

4.2 群落信息有向交互分析

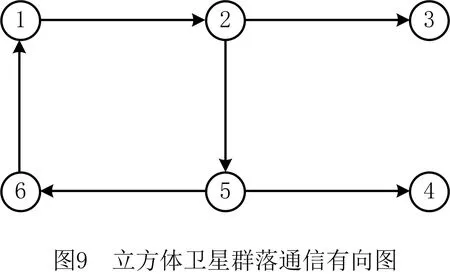
在另一种通讯模式中，考虑群落中6个立方体卫星的信息交互是有方向性的，绘制的图G∈(V,E)由图9给出。从方向图G中可以看出，群落中的通讯方式是单向的，即：立方体卫星1能够将信息传输给立方体卫星2，但是立方体卫星1不能接收到立方体卫星2的信息。以此类推，2能够将信息传输给3，2能够将信息传输给5，5能够将信息传输给4，5能够将信息传输给6，6能够将信息传输给1。由此得到，立方体卫星群落通信网络图形G的顶点集合V={v1,v2,v3,v4,v5,v6}，边的集合E={(v1v2),(v2v3),(v2v5),(v5v4),(v5v6),(v6v1)}。

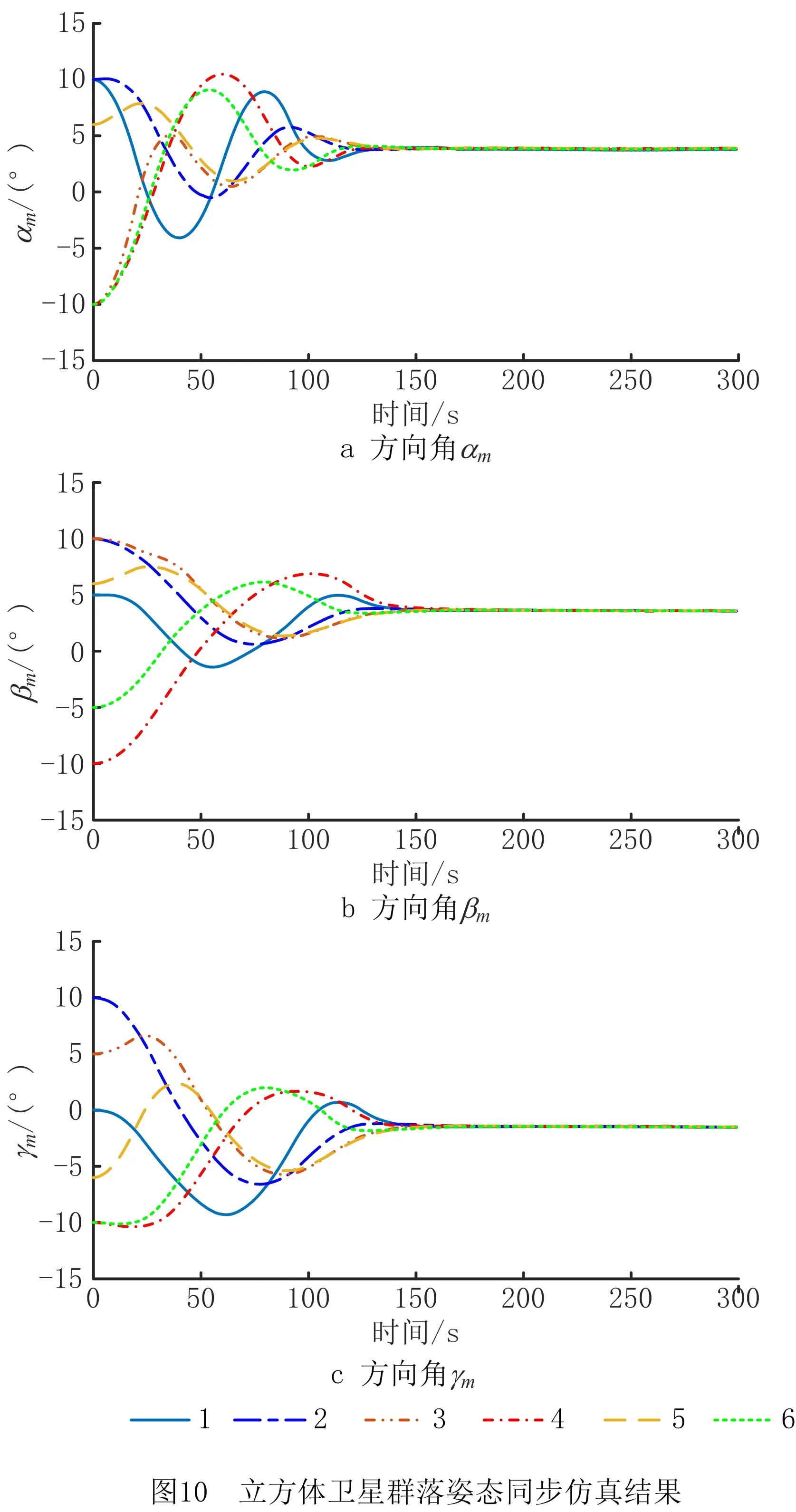
下面给出基于信息有向交互模式的仿真分析结果。选择控制器参数ηij=1，Γi=diag{1,1,1}，i=1,…,6。表4给出了6个立方体卫星的姿态控制模块中各自配置的8个μ-PPT推进器的脉冲数目。图10分别给出了群落中6个立方体卫星三个姿态角分量的仿真结果。结果表明，在提出的姿态同步控制策略以及μ-PPT脉冲推进器作用下，6个立方体卫星由不同的初始姿态角最终趋于同步姿态角度[αmean;βmean;γmean]=[3.8°;3.6°;-1.5°]。

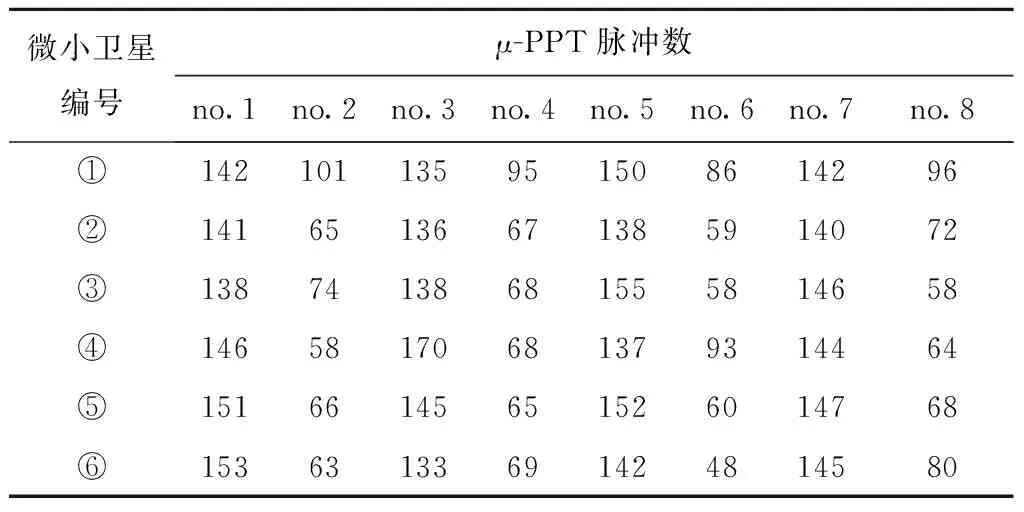
表4 μ-PPT脉冲序列数

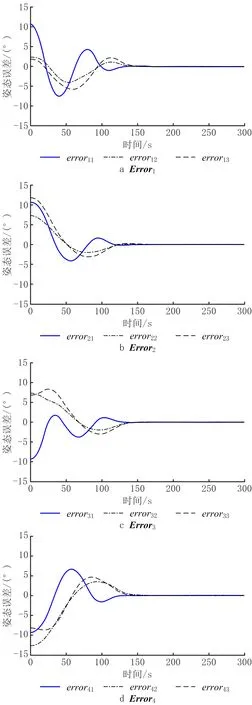
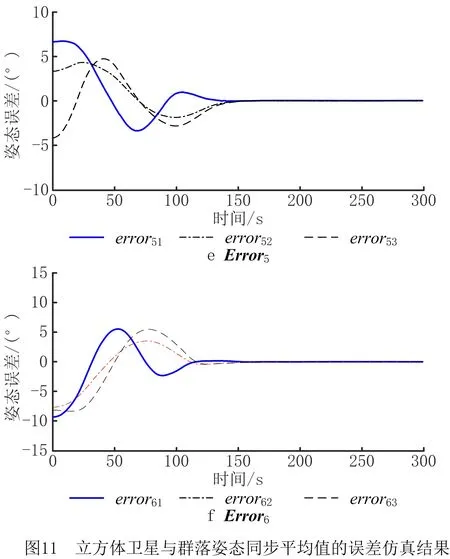
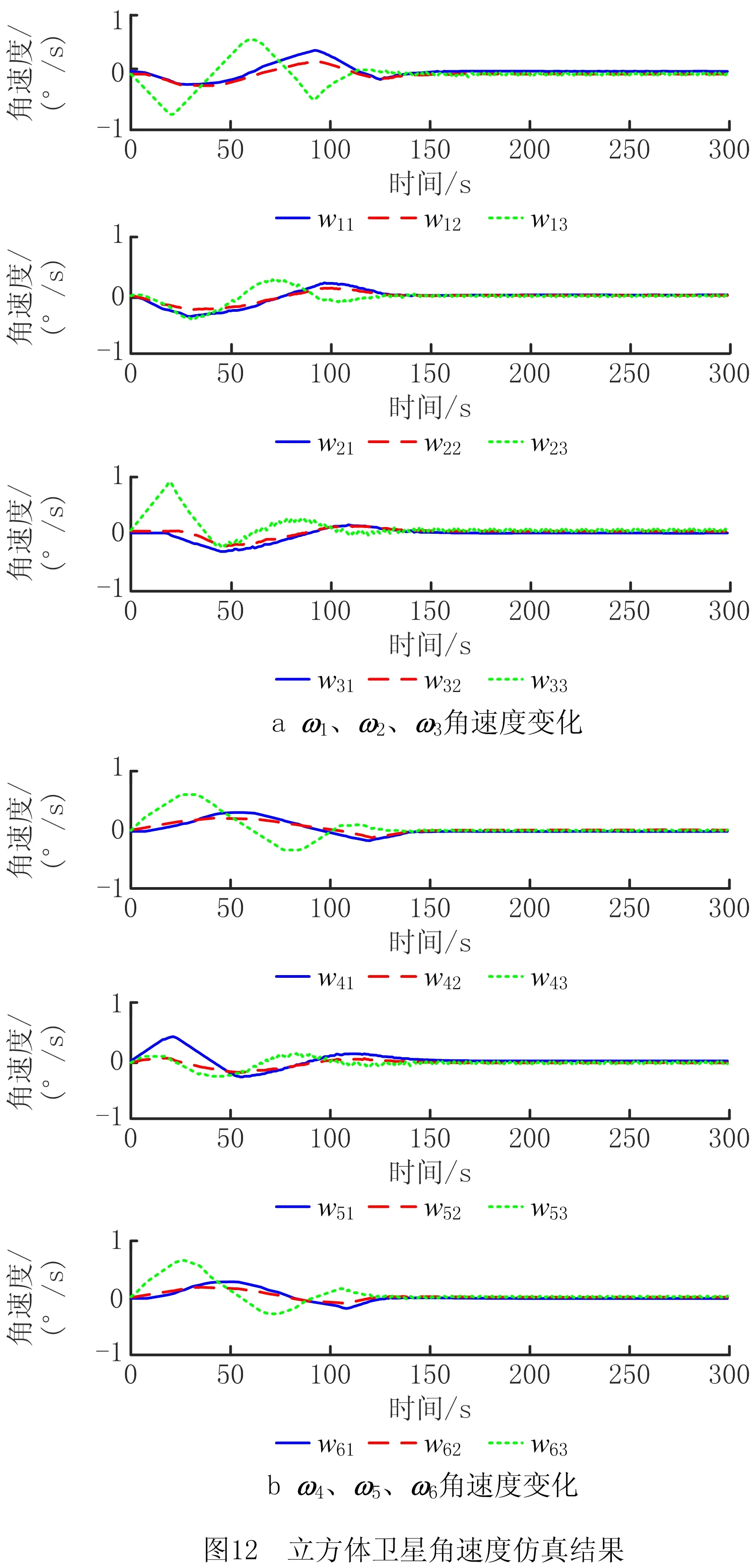
基于群落姿态同步检验标准式(21)，图11所示的仿真结果表明，第2个案例中每个立方体卫星与群落整体的姿态同步均值的误差随时间趋于零。图12给出了群落中6个立方体卫星角速度ωi分量随时间演变的仿真结果。结果表明，在群落内小卫星之间的信息交互有指向性的情况下，每个立方体卫星的姿态同步误差以及角速度最终也能满足式(4)提出的任务目标。

对比以上两种不同的群落内部信息交互模式，可以看到，由于每个立方体卫星对周围信息获知差异，群落姿态同步结果也不同。此外，群落通信网络也可以同时存在无向交互和有向交互两种混合模式。根据控制算法的证明分析以及第四部分的案例分析可知，基于本文提出的控制策略，在混合信息交互模式下，依然能够满足群落姿态同步目标。

5 结束语

多个立方体卫星组成的微小卫星群落容错率高，相比于单个普通卫星更能发挥出它们的优势。本文基于标准模块化结构的多单元体立方体卫星，提出一种基于μ-PPT电推进系统的微小卫星群落姿态同步控制策略。基于群落姿态动力学模型，构建的自适应控制器能够根据每个立方体卫星与邻接卫星的状态信息差异，通过对同步信号变量进行互联强度加权，改善群落姿态同步性能。并且，基于Lyapunov稳定性理论，对群落整体动态稳定性和收敛性进行了验证。此外，立方体卫星的离散μ-PPT电推进系统通过最优脉冲序列配置方法，能够在实现群落整体姿态同步的同时，实现对外部干扰力矩的连续补偿与稳定。基于立方体卫星群落在不同信息交互方式下的姿态协同控制案例分析，验证了所提出控制策略的自适应动态性能和有效性，为微小卫星群落协同控制提供了一个新思路。与此同时，后续工作将进一步引入微小卫星的空间平移运动，研究微小卫星有限体积下的平动和转动推进器的选择及其部署方案，研究在空间环境下微小卫星群落平移与姿态的协同运动及其同步控制策略，研究群落内部通信可靠性和实时性对微小卫星协同控制的影响并提出解决方案。