考虑多时间因素的绿色可重入混合流水车间调度问题
耿凯峰,叶春明
(1.上海理工大学 管理学院,上海 200093;2.南阳理工学院 信息化建设与管理中心,河南 南阳 473004)
0 引言
随着能源价格的不断上涨和环境问题的日益严峻,制造企业面临着巨大的困难和挑战。根据2020年全球能源分析报告,在经济增长放缓的背景下,全球能源消耗自1990年~2019年期间呈现逐步增长的趋势,与2000年~2018年期间平均每年2%的增长率相比,中国的能源消费增速虽然低于前几年,但一直以来是全球最大的能源消费国[1]。另外,国家统计局公布的数据显示,2017年中国第二产业用电量占比高达66%以上,而制造业占第二产业用电量的55%[2]。可重入混合流水车间调度问题(Re-entrant Hybrid Flow shop Scheduling Problem, RHFSP)广泛应用于工业领域中,如印刷电路板、薄膜晶体管液晶显示器面板制造以及半导体行业等。由于RHFSP涉及工序和设备较多,大多为高耗能行业,探索节能降耗减排机制,开展绿色车间调度研究,对实现碳达峰、碳中和目标任务,建立环境友好型社会具有重要意义。
通常情况下,引进节能设备、更新制造工艺是实现节能减排最直接的手段。但是,上述手段往往需要投入巨大资金,耗费大量的人力物力,并且周期长风险大。研究发现,除了更新生产线以外,采用合理的生产运作方法和优化策略是实现节能减排的另一种手段。作为实现绿色制造的重要环节,绿色调度通过资源分配、工序排序和生产运作方法的合理优化,达到节能降耗降成本的目的,从而实现经济指标和环境指标的协同优化。近年来,关于绿色调度问题的研究已经取得了一些成果。吴秀丽等[3]提出了改进的NSGA-Ⅱ求解考虑机器多转速的柔性车间绿色调度问题,并研究了开关机状态、空载状态、加工状态以及待机状态对优化目标的影响。DING等[4]提出了NEH(Nawaz-Enscore-Ham)算法和迭代贪婪算法求解置换流水车间调度问题,以最小化总碳排放量和最大完工时间为目标。雷德明等[5]提出一种新型蛙跳算法求解以最小化总能耗和总延迟时间为目标的低碳混合流水车间调度问题。孟磊磊等[6]研究了面向节能的工艺规划与调度集成问题,并建立了3种考虑关机重启节能策略的混合整数规划模型。CHE等[7]采用混合整数规划模型求解分时电价下的单机调度问题,以最小化电能成本为优化目标。在分时电价背景下,耿凯峰等[8]提出一种改进的多目标文化基因算法求解以最小化最大完工时间、总能耗成本和总碳排放为目标的绿色RHFSP。LEI等[9]设计了一种基于帝国竞争算法和变邻域搜索算法的两阶段元启发式算法,以解决具有总能耗约束的多目标柔性流水车间调度问题。周炳海等[10]提出一种改进差分进化算法求解考虑能耗和准时的双目标混合流水车间调度问题。姚友杰等[11]提出了改进分布估计算法求解以最小化最大完工时间和总能耗为目标的绿色零等待作业车间调度问题。李聪波等[12]研究了考虑设备预维护的柔性作业车间调度问题,分析了机器预维护对切削加工能耗、工件装夹拆卸能耗、换刀能耗以及对刀能耗的影响,并以总能耗和最大完工时间为优化目标。ZHENG等[13]提出一种多目标果蝇优化算法,以最小化制造时间和总碳排放为目标,解决资源受限的无关并行机器调度问题。李俊青等[14]提出一种改进人工蜂群算法求解考虑运输资源约束的柔性车间调度问题,并以总能耗和最大完工时间为优化目标。针对分布式低碳调度问题,潘子肖等[15]提出了基于问题特性的NSGA-Ⅱ算法,并以最小化总延迟时间和总能耗为优化目标。
不难发现,以往的研究重点关注加工时间,而弱化了调整时间、运输时间等辅助过程对能耗的影响。制造企业调查统计表明[16]:在制造过程中,非加工时间占整个生产时间的90%以上。因此,考虑辅助时间更加贴近实际情况,有必要对辅助时间进行深入的研究。文献[17]对考虑调整时间的作业车间调度问题的国内外研究进行了综述。LI等[18]提出一种具有能量感知的多目标优化算法求解考虑调整能耗的混合流水车间调度问题。KARIMI等[19]将运输时间引入柔性作业车间调度问题中,并用两个混合整数线性规划模型对该问题进行求解。DAI等[20]采用增强遗传算法求解考虑运输时间约束的多目标绿色柔性流水车间调度问题,并以最小化最大完工时间和能耗为优化目标。李明等[21]提出一种新型帝国竞争算法求解考虑顺序相关调整时间(Sequence Dependent Setup Times, SDST)和关键目标的低碳柔性作业车间调度问题。LI等[22]提出一种改进的Jaya算法来解决同时考虑运输时间和调整时间的多目标柔性作业车间调度问题。LIOU等[23]采用混合遗传算法研究了考虑运输时间和SDST的单目标多阶段流水车间调度问题。JIANG等[24]提出一种改进的基于分解的多目标进化算法求解考虑SDST的绿色置换流水车间调度问题,并以最小化完工时间和能耗为优化目标。王建华等[25]提出一种自适应Jaya算法求解考虑调整时间的绿色并行机调度问题。
在保证产品质量的前提下,合理优化资源配置,探索节能减排机制,对提高企业竞争力、构建环境友好型社会具有重要意义。从现有文献来看:①有关节能减排的调度研究,主要集中在柔性流水车间、柔性作业车间、混合流水车间以及置换流水车间等领域,而在RHFSP中的相关研究较少。②在以往的研究中,调整时间和运输时间通常被忽略或者放在加工时间中考虑,同时考虑调整时间和运输时间等多时间因素的RHFSP的研究更少。基于此,本文以考虑SDST和运输时间的RHFSP为研究对象,提出一种混合文化基因算法(Hybrid Memetic Algorithm, HMA)求解以最小化最大完工时间和总能耗为优化目标的绿色调度问题。为了提高算法的性能,设计了基于工序、机器和转速的三层编码方法、基于贪婪机器选择和完全随机的混合种群初始化方法、交叉和变异算子、五种邻域搜索算子以及节能算子。最后,通过仿真实验验证了该算法求解GRHFSP-MTF的优越性。
1 问题描述和数学建模
1.1 问题描述

除了经典流水车间调度问题的假设以外,本文主要假设如下:每个工件的可重入次数,各道工序的标准加工时间,机器的单位加工能耗、空闲能耗和加工速度,调整时间以及运输时间已知;机器单位耗能与其加工速度有关,且成正比关系;为了减少机器的待机时间,所有机器开始加工首道工序时开机,末道工序完工时关机;运输资源(如AGV)数量完全满足运输需求,并且在运输过程中互不影响;每个机器上首道工序的调整时间忽略不计;不考虑机器故障时间以及机器开关机能耗;每个工序的加工过程中加工速度保持不变。
多时间因素下,GRHFSP-MTF主要包含工件排序、机器分配和速度选择3个子问题。由于具有可重入特性,GRHFSP-MTF涉及工序和设备较多,属于典型的较大规模组合优化问题,采用精确算法或者模型求解难度较大,本文提出一种混合文化基因算法(HMA)求解该问题。调度目标是将工件合理地安排到各机器上并确定机器的加工速度和工件的加工次序及加工时间、调整时间以及运输时间等等,在满足各种约束条件的情况下,使最大完工时间Cmax和总耗能成本TE最小。
1.2 数学符号
n为工件总数;
j,j′,h,f为工件序号,j,j′,h,f=1,2,…,n;
s为工位总数;
repeat为重入次数;
i,i-为工位序号,i=1,2,…,s;
mi为工位i中的并行机器数量;
l为工位i中的机器序号,l=1,2,…,mi;
Mtotal为机器的总数,Mtotal=m1+m2+…+ms;
o,u为所有机器的编号,o,u=1,2,…,Mtotal;
Nj为工件j的工序总数;
k,k′,z为工序序号,k=1,2,…,Nj;


Ojk为工件j的第k道工序;
M为一个足够大的正数;
Pjk为工序Ojk的标准加工时间;
d为机器不同的加工速度的个数;
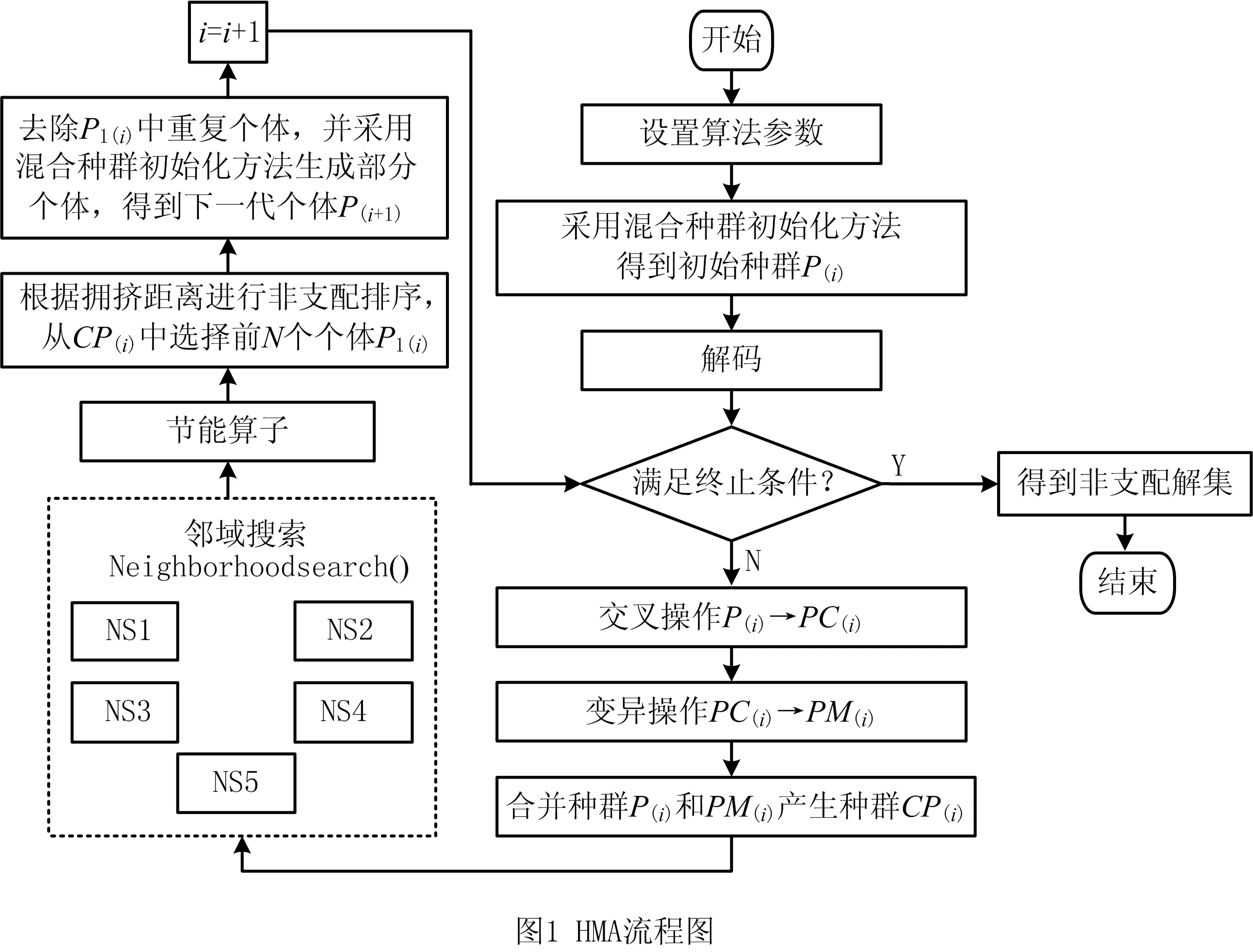
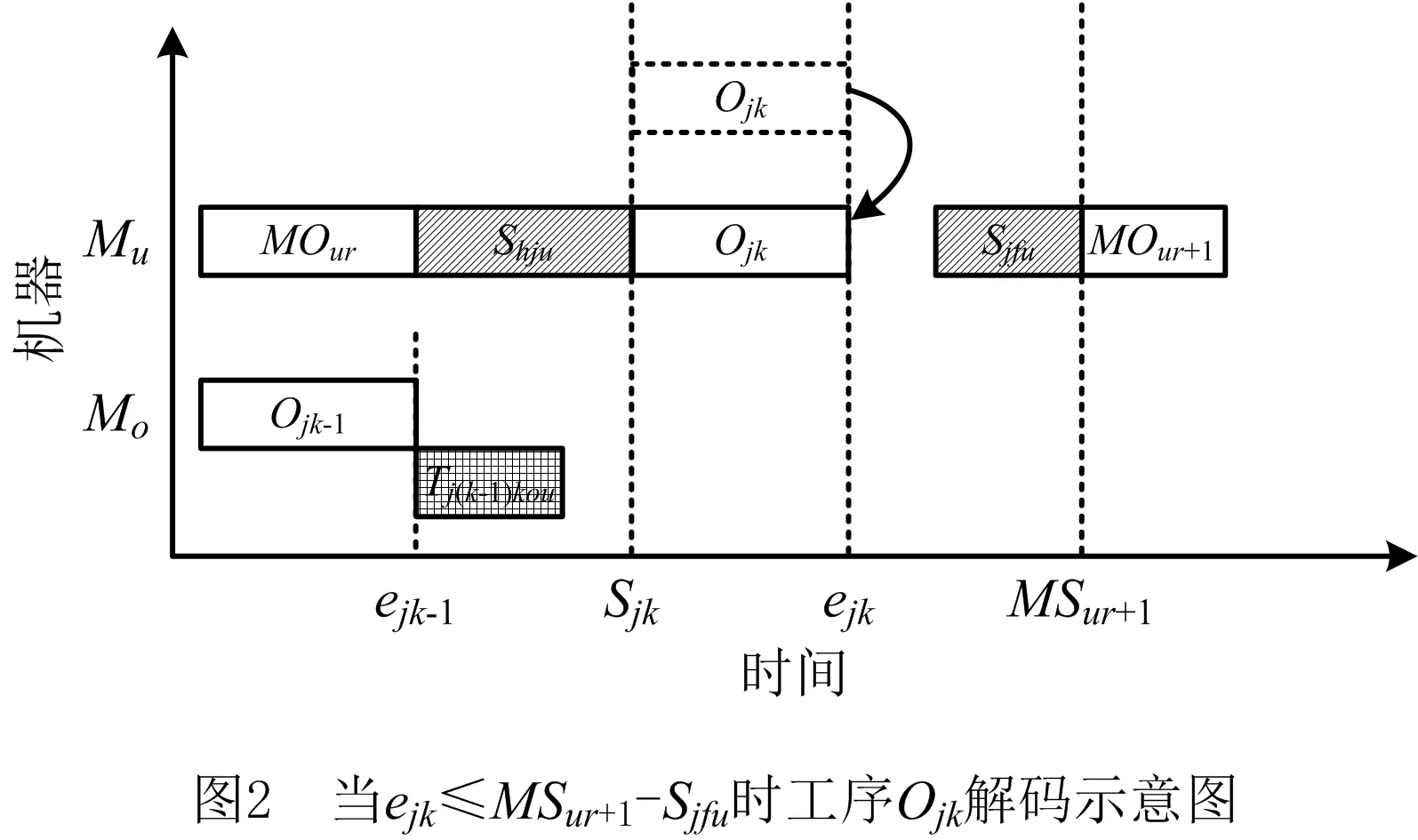
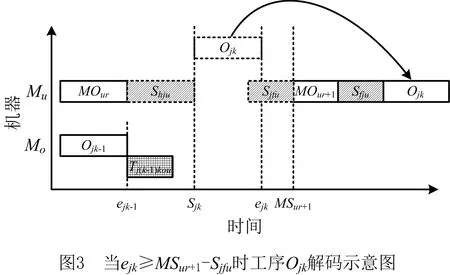
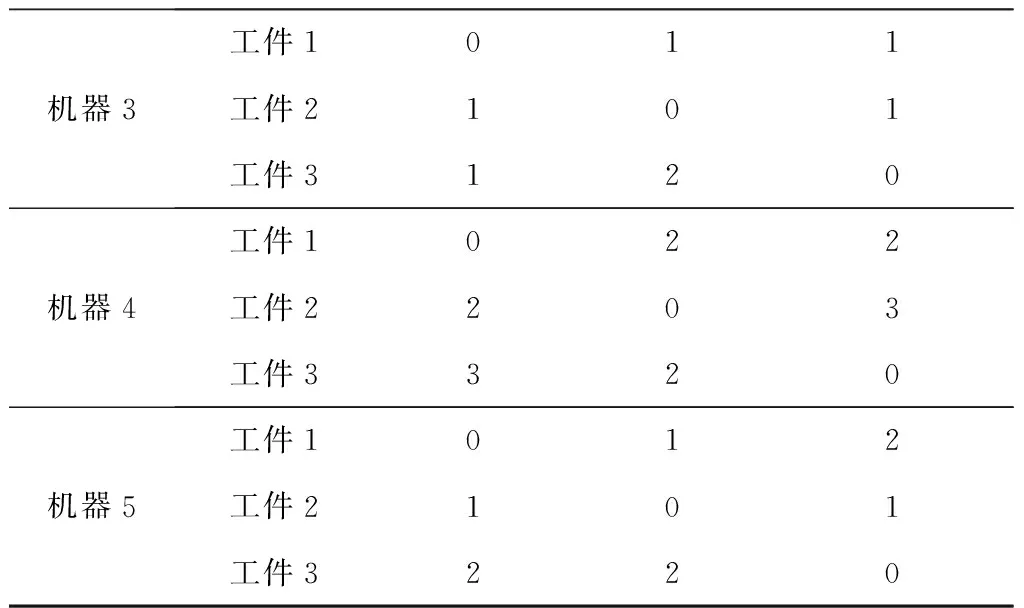
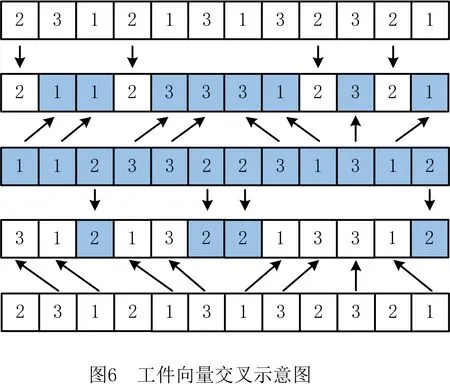
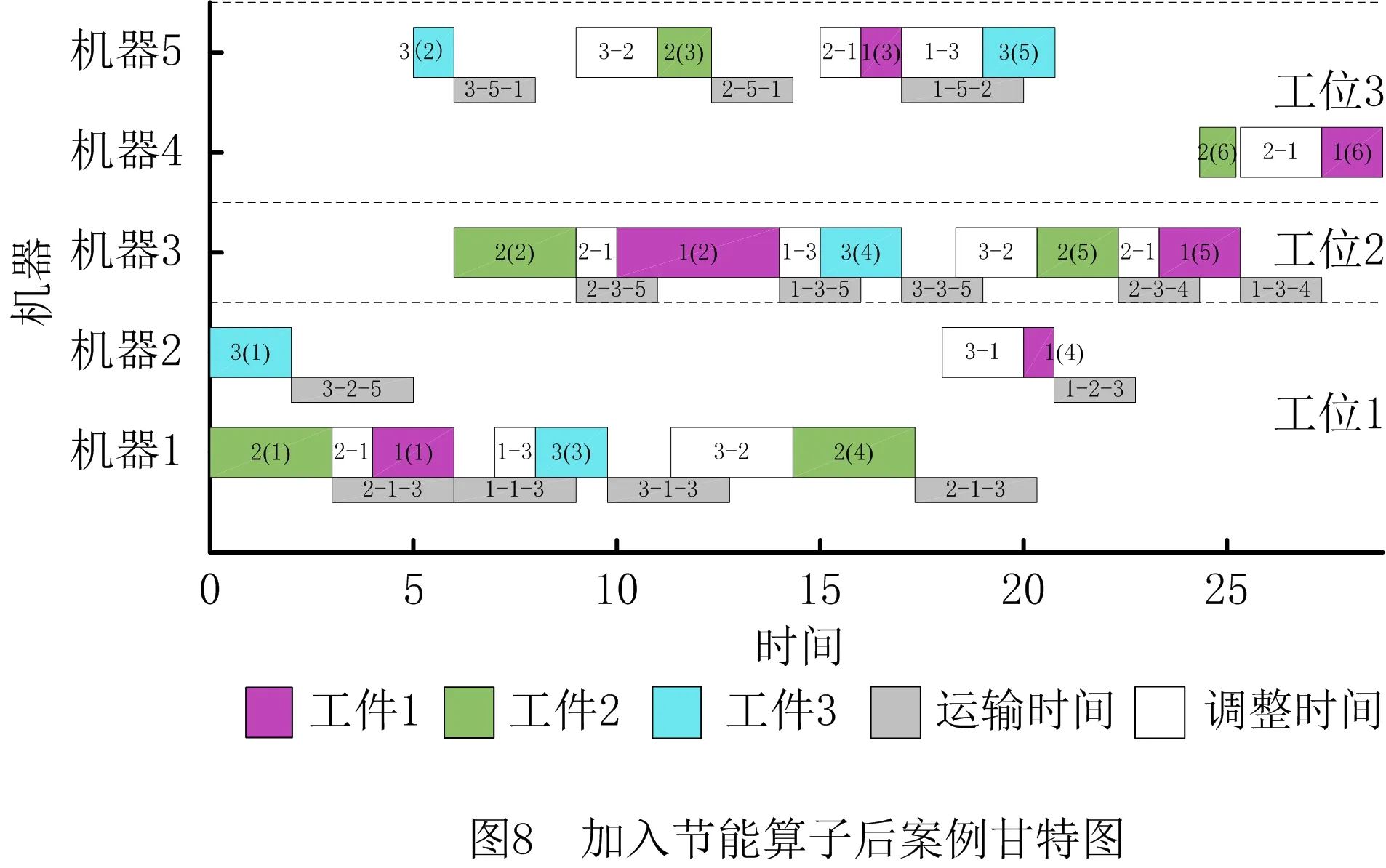
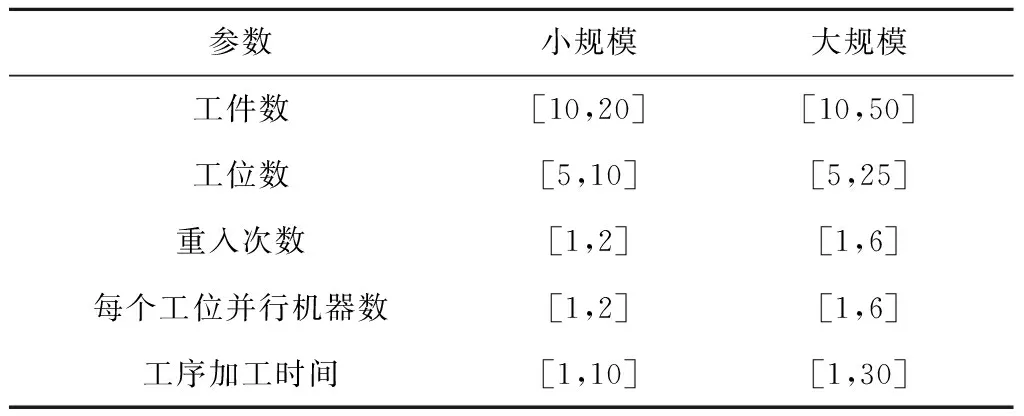
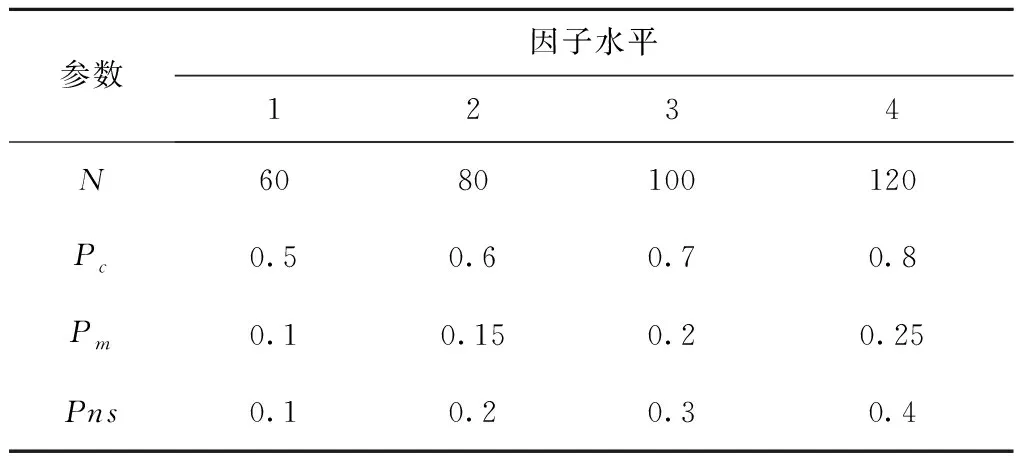
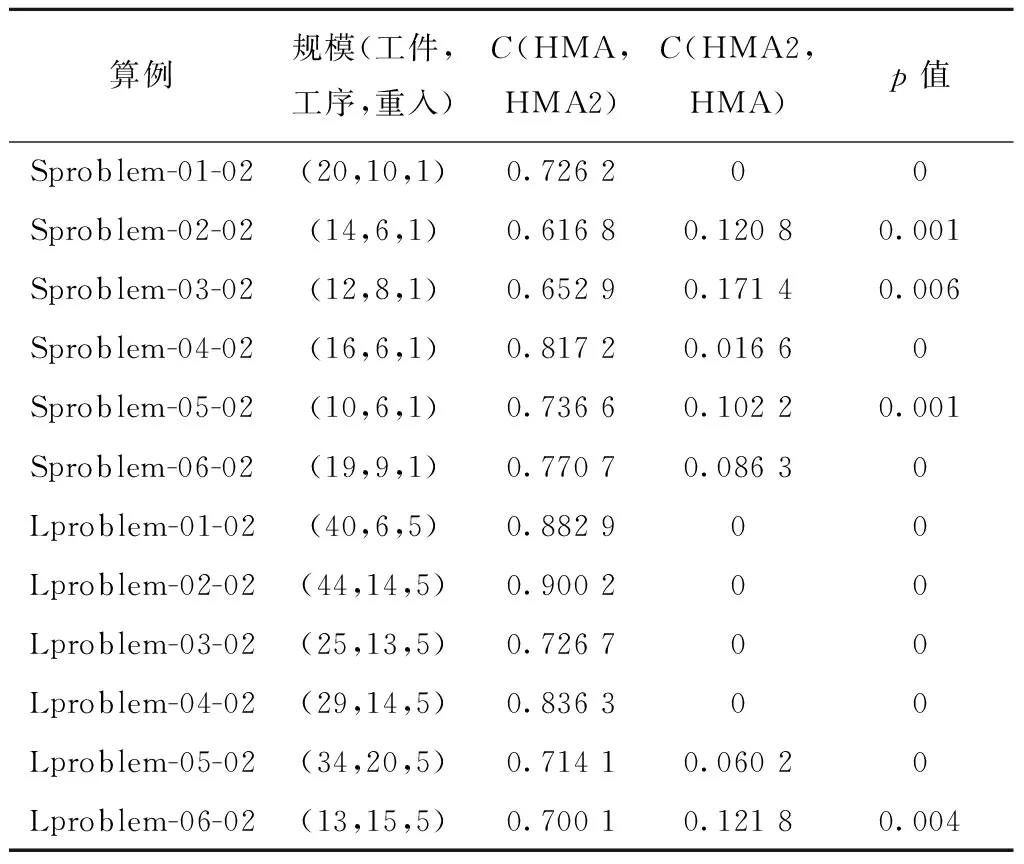
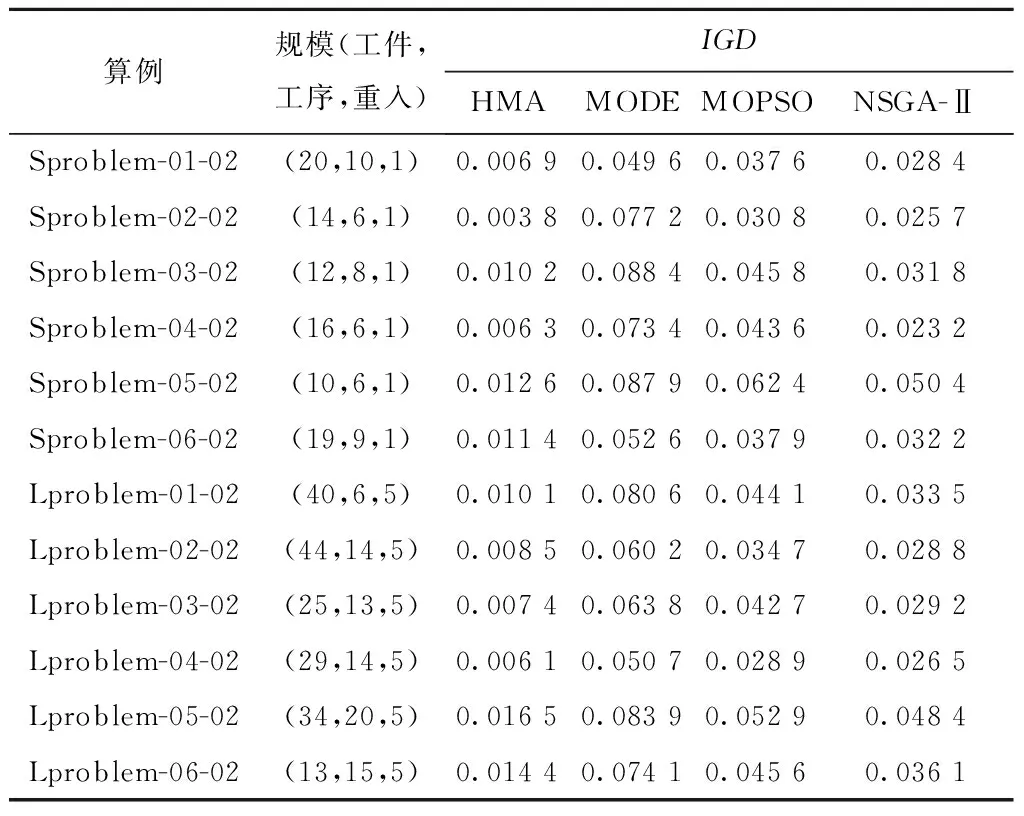
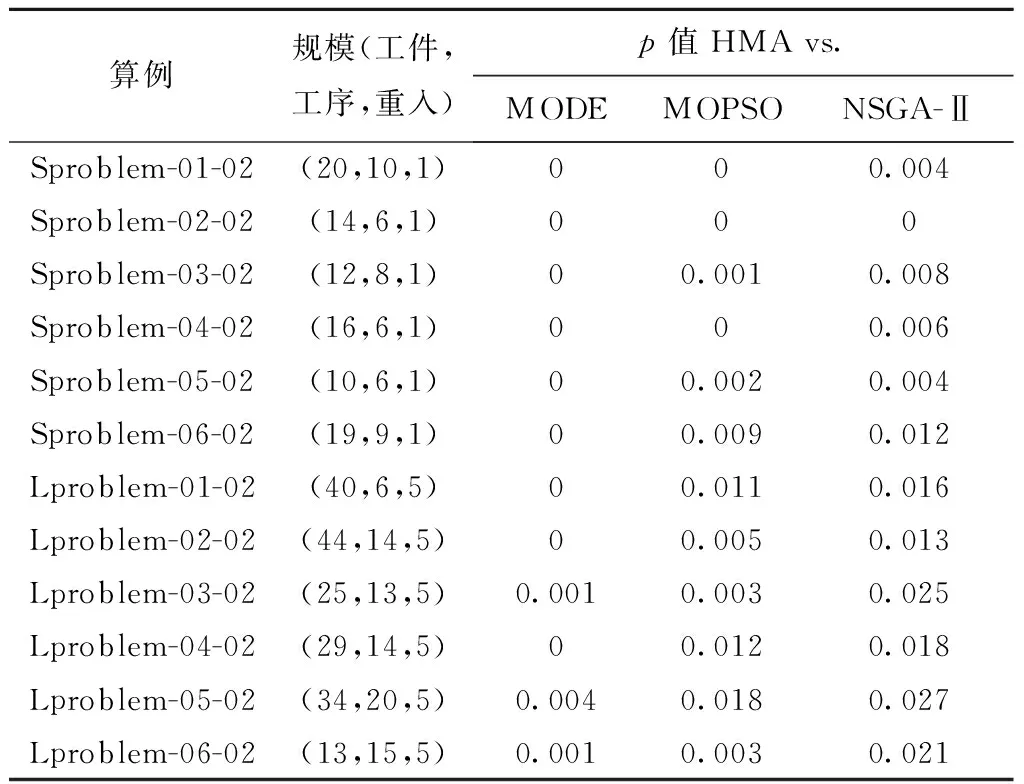
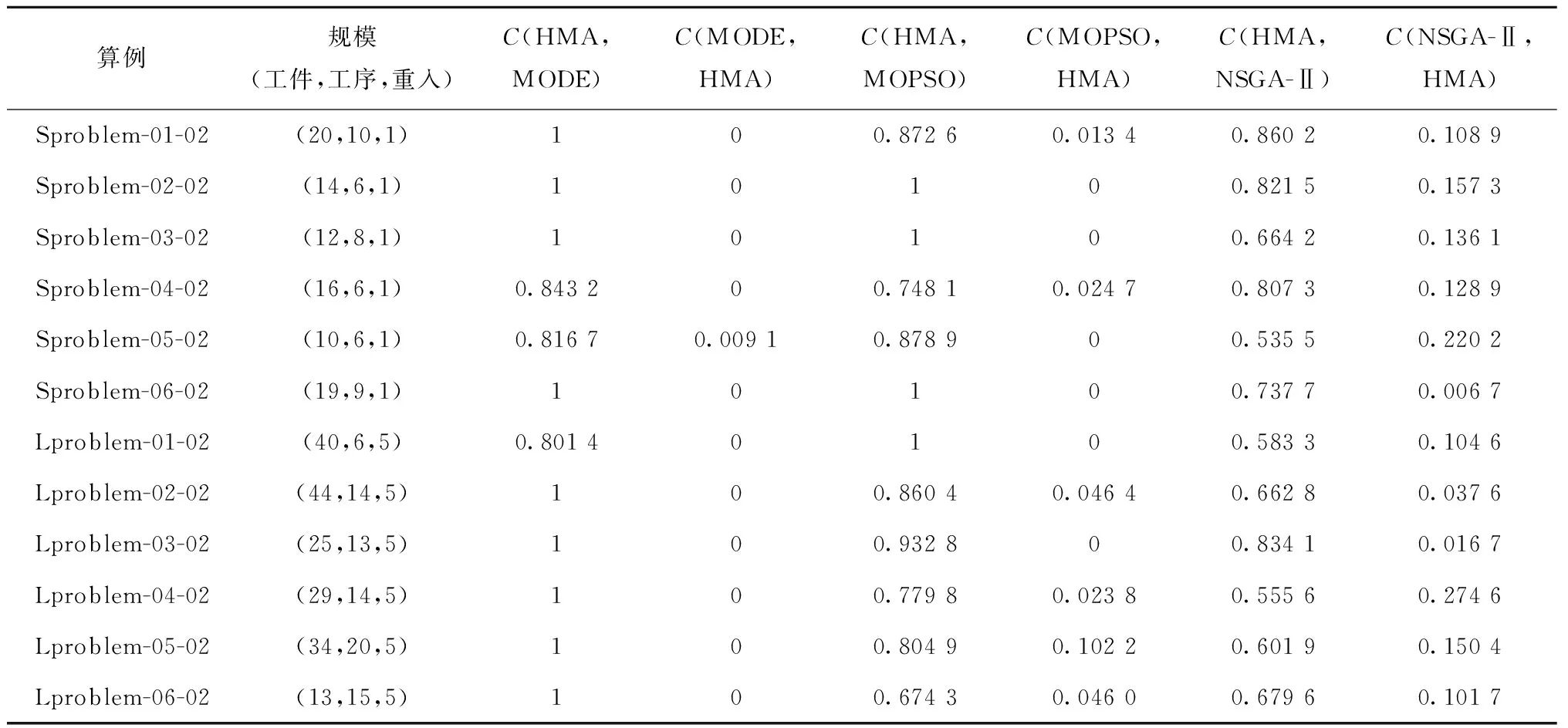
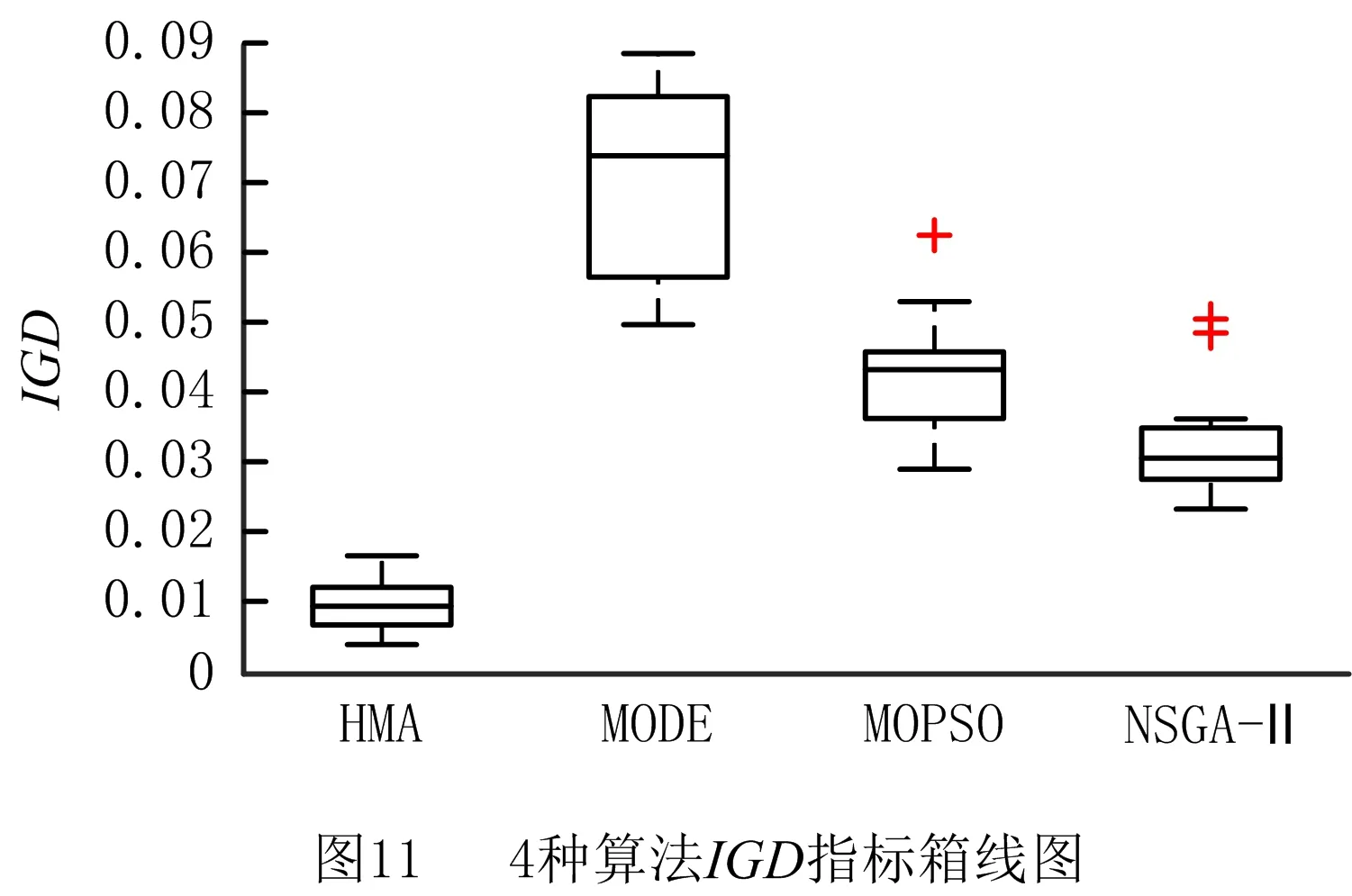
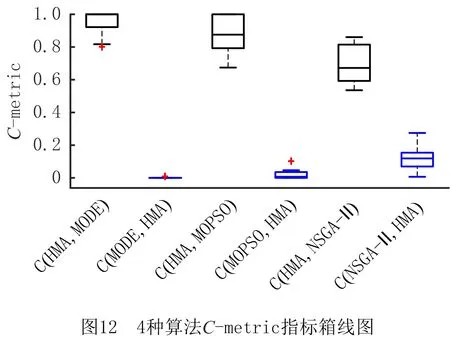
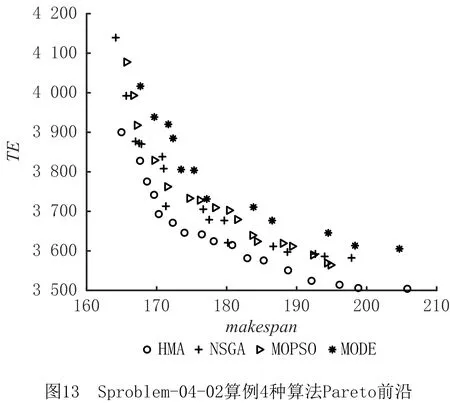
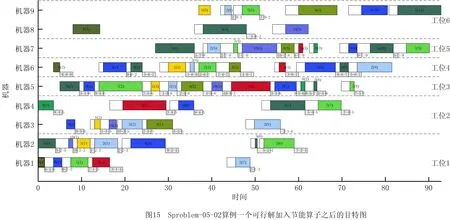
vq,vq′为机器加工速度,q,q′=1,2,…,d,且v1 sjk为工序Ojk的开始时间; ejk为工序Ojk的完工时间; Tj(k-1)kou为工件j的两个连续工序Oj(k-1)和Ojk从机器o到机器u的运输时间; Cj为工件j的完工时间; MSor为机器o上第r道工序的开始时间; MCor为机器o上第r道工序的完工时间; MOor为机器o上第r道工序; Eidle为机器空闲时的单位能耗; Etp为AGV运输时间单位耗能; Esetup为机器调整时间单位耗能; Ui为在工位i中加工的所有工序的集合; ∀o,q; ∀o; ∀o; ∀i,j,k,l; ∀j,j′,k,k′; 目标函数: 最小化最大完工时间Cmax,即makespan,如式(1)所示: minCmax=maxCj。 (1) 总耗能成本TE主要由机器的加工状态总能耗TEbusy、空转状态总能耗TEidle、运输总能耗TEtp和调整状态总能耗TEsetup四部分组成,如式(2)所示: minTE=TEbusy+TEidle+TEtp+TEsetup。 (2) TEbusy为所有机器处于加工状态时的总能耗,如式(3)所示: (3) TEidle为所有机器处于空转状态时的总能耗,空转能耗主要是指在机器完成当前工序加工,等待下一道工序到达这段时间的能耗,如式(4)所示: (4) TEtp为运输能耗成本,是指所有工件通过AGV在不同机器间运输时的总能耗,如式(5)所示: (5) TEsetup为调整状态总能耗,主要指同一机器加工两个相邻工序进行相关调整(如更换刀具、模具、夹具、装卸、调试等)时所消耗的能耗,如式(6)所示: (6) 主要约束条件如下: (7) (8) ∀i,i-,j,q,k={1,2,…,Nj-1}; (9) ejk=sjk+Pjkq; (10) M(2-rijkl-rij′k′l)+M(1-Zjkj′k′)+ (sj′k′-sjk)≥Pjkq,∀i,q,j,j′,l,Ojk∈Ui,Oj′k′∈Ui; (11) M(2-rijkl-rij′k′l)+M×Zjkj′k′+(sjk-sj′k′)≥ Pj′k′q,∀i,q,j,j′,l,Ojk∈Ui,Oj′k′∈Ui; (12) M(2-rijkl-rijk′l)+(sjk′-sjk)≥Pjkq, ∀i,q,k (13) ejk-1+Tj(k-1)kou≤ejk-Pjkq+M(1-yjkou), ∀j,q,o,u,k={2,…,Nj}; (14) Pjkq+M(1-xjko(r+1)),∀j,h,o,q,z, (15) (16) Cj≤Cmax,∀j。 (17) 其中:式(1)和式(2)为目标函数;式(3)~式(6)为4种能耗表达式;式(7)表示从开机到关机,只能包含空闲,加工和调整3种状态;约束(8)保证每道工序只能在相应工位中的一台机器上加工;约束(9)确保工序Oj(k+1)的加工开始时间不早于Ojk工序的加工完成时间;约束(10)为工序的开始时间和结束时间约束;约束(11)~约束(13)确保每台机器在同一时刻最多加工一道工序;约束(14)确保当前工序的开始时间不小于前一道工序完工时间与运输时间之和;约束(15)确保在某台机器上当前工序的开始时间不小于该机器前一道工序的完工时间与两道工序间的调整时间之和;约束(16)和约束(17)规定了工件的完工时间。 文化基因算法(memetic algorithm)是由Norman和Moscato于1991年提出的一个由进化算法与局部搜索相结合的通用算法框架。通过在全局和局部搜索过程之间建立动态平衡,文化基因算法在很多领域有着广泛的应用[26-30]。针对GRHFSP-MTF问题的特点以及各种约束,本文基于NSGA-Ⅱ设计了混合文化基因算法,主要包括编码与解码策略、混合种群初始化方法、交叉变异算子、5种邻域搜索算子,以及节能算子等,算法流程如图1所示。 为了最大限度地表征问题的解空间,基于GRHFSP-MTF的3个子问题:工件排序、机器分配和速度选择,本文采用三层编码方式表示个体,包括工序向量、机器向量和速度向量3部分,且每部分编码长度等于所有工件的工序之和。 (1)工序向量 采用基于工序的整数编码方式,每个基因用工件序号表示,并且同一个工件号出现的先后次序表示该工件的不同工序。例如工序部分编码为[2 3 1 2 1 3],其中:第一个2表示工件2的第一道工序,第二个2表示工件2的第二道工序,以此类推,对应工序的加工顺序为O21-O31-O11-O22-O12-O32。 (2)机器向量 由n部分组成,每部分表示某一工件所有工序对应的机器。另外,从1开始对机器进行编号,机器的总数为所有工位的机器个数之和。 (3)速度向量 由n部分组成,每部分表示某一工件所有工序对应的加工速度。每个机器可以选择不同的加工速度来加工工件,不同加工速度的单位能耗不同,工序的加工时间不同。 根据三层编码方式,从左到右依次读取工序排序部分的基因,确定所有工序的前后加工次序,同时根据工序对应的机器向量部分确定所选用的加工机器,然后根据速度向量部分确定工序的加工速度,进而得到每个工序对应的实际加工时间、调整时间以及运输时间等信息,最后计算出该工序的开始加工时间和完工时间。具体步骤如下: 步骤1从工序排序部分选择一个基因,转换为对应的工序Ojk。 步骤2根据机器选择部分确定工序Ojk的加工机器u。 步骤4确定工序Ojk的最早开始加工时间sjk和完工时间ejk,如式(18)和式(19)所示: sjk=max{ej(k-1)+Tj(k-1)kou,pu+Sjhu}; (18) ejk=sjk+Pjkq。 (19) 其中:ej(k-1)为工件j的上一道工序的完工时间;Tj(k-1)kou为工件j的两个连续工序Oj(k-1)和Ojk从机器o到机器u的运输时间;pu表示机器u的上某道工序的完工时间;Sjhu为工件j和h在机器u先后顺序加工时,两道工序之间的顺序相关调整时间,且Sjhu≠Shju,另外,当j=h时,Sjhu=0。 步骤5为工序Ojk寻找合适的插入点,确定工序Ojk在机器u上的实际开始加工时间和完工时间,解码示意图如图2和图3所示。具体过程如下: (1)获取机器u上当前所有的工序集合OPS,并依照完工时间升序排列;(2)获取OPS中第r道工序的完工时间MCur,令pu=MCur,其中,r=0表示将工序Ojk作为设备首道工序,此时pu=MCur=0;(3)根据式(18)和式(19)计算工序Ojk的开始加工时间sjk和完工时间ejk。若第r道工序为机器Mu上的最后一道工序,则返回sjk和ejk,结束判断;否则,若ejk≤MSur+1,其中MSur+1为机器Mu上第r+1道工序的开始时间,则返回sjk和ejk,结束判断;否则,判断下一道工序r+1,转步骤5(1)继续。 步骤6重复执行步骤1~步骤5,直到工序选择部分遍历完毕。 步骤7记录每个工序的开始加工时间和完工时间,调整时间,运输时间、机器分配及加工速度等信息。 步骤8计算两个目标函数值Cmax和TE。 表1 标准加工时间 表2 运输时间 表3 调整时间 续表3 由图4可知,该个体共有3个工件18道工序,每个工件6道工序。以图4中个体为例,在各种条件的约束下,解码后所得调度方案甘特图如图5所示,两个目标函数分别为Cmax=28.83和TE=274.08。如图5所示,加工时间为0的工序不在甘特图上显示,2(1)表示工件2的第一道加工时间为非0的工序,另外,在机器1上,调整时间块2-1表示在机器1上工件2和工件1之间的顺序相关调整时间,运输时间块2-1-3表示工件2需要从机器1运输到机器3进行下一道工序的加工,以此类推。 根据三层编码策略,解空间足够大,采用完全随机方法初始化种群会严重影响算法的求解效果。种群初始化是HMA的关键组成部分,高质量和多样性的初始种群可以使算法更快地收敛。为了提高初始种群解的质量和多样性,本文采用贪婪机器选择和完全随机两种方式混合生成初始化种群,伪代码如下: 算法1Population_initialization()。 输入:种群规模N; 输出:初始化种群。 1: 随机生成工件向量部分,长度为所有工序的总和,每个工件出现repeat×s次。 2: for pop=1∶N 3: if rand1< 0.5 %rand1为[0,1]之间随机变量 4: 从左到右遍历工件向量部分,根据运输时间和调整时间等约束,从所有可用机器集合中贪婪选择开工时间最早的机器分配给当前工序。如果多台机器同时满足条件,则选择使该工序调整时间较短的机器,同时随机选择机器的加工速度。 5: else 6: 从左到右遍历工件向量部分,为所有工序从可用机器集合中随机分配一台机器,并随机设置机器加工速度。 7: end if 8: end for 9: 输出初始化种群。 根据GRHFSP-MTF的特点和各种约束,并非每个工序都能被所有机器加工。如果将工件、机器以及速度3部分直接交叉,将会产生大量的非可行解。为了保证解的可行性,避免交叉后修复,本文设计了两种交叉策略。在工件向量部分采用JBX(job-based crossover)交叉策略。首先,将工件随机分为两个子集set1和set2;然后,分别将父代P1和P2中属于set1中工件的基因复制到相同位置的子代O1和O2中;最后,分别将父代P2和P1中属于set2中工件的基因依照原有顺序依次添加到子代O1和O2中。工件向量部分交叉过程如图6所示,其中set1=[2]和set2=[1,3]。在机器向量和速度向量部分采用与上述过程类似的策略。首先,将工位分为两个集合set3和set4;然后,将父代PM1和PM2中属于set3工位上的所有工序分别复制到子代M1和M2中;再次,将父代PM1和PM2中属于set4工位上的所有工序分别复制到子代M2和M1中。以机器向量部分交叉过程如图7所示,其中set3=[2]和set4=[1]。 变异操作通过随机改变染色体的某些基因对染色体产生较小扰动来生成新的个体,它可以增加种群的多样性并在一定程度上影响算法的局部搜索能力。为了保证变异后解的可行性,本文设计了两种变异策略。在工件向量部分采用两点交换变异策略,即在工件向量中随机选择两个基因位置r1和r2,并交换r1和r2位置的基因。在机器和速度向量部分采用单点变异策略,即在机器向量或者速度向量中随机选择一个位置r3,将r3位置的基因改为同工位其他机器或者随机改变加工速度。 交叉和变异过程虽然在一定程度上可以提高种群的多样性,但是带有一定的随机性,较难保证种群的质量朝着好的方向进化。另外,减少负载最大的机器上的工序数量、提高部分工件的加工速度、交换工件的加工顺序有助于降低makespan,降低负载最小的机器上工件的加工速度有利于降低能耗。为了减少种群的退化现象,基于求解问题的特点和借鉴模拟退火算法思想,本文共设计了5种不同的邻域搜索算子。 算法2Neighborhoodsearch()。 输入:个体X,回退概率Pns; 输出:更新后的个体X。 1: R←randperm(5,1) %随机生成[1,5]之间的整数 2: switch (R) 3: case 1:执行NS1(X),得到新个体X′ 4: case 2:执行NS2(X),得到新个体X′ 5: case 3:执行NS3(X),得到新个体X′ 6: case 4:执行NS4(X),得到新个体X′ 7: case 5:执行NS5(X),得到新个体X′ 8: end switch 10: X←X′ 11: else if rand2 12: X←X′ 13: end (1)NS1 选择负载最大的机器并减少该机器上的工序数量,具体步骤如下: 步骤1从种群中随机选择个体X,根据解码策略生成的调度方案计算每个机器负载。 步骤2选择负载最大的机器o。 步骤3随机选择机器o上的工序Ojk。若工序Ojk所在的工位有多台并行机,则选择同工位的其他机器u加工Ojk。若工序Ojk所在的工位仅有一台机器o,则机器o使用最快的速度加工工序Ojk。 步骤4计算新个体X′的目标函数值。 (2)NS2 选择负载最大的机器并提高该机器上工序的加工速度,具体步骤如下: 步骤1从种群中随机选择个体X,根据解码策略生成的调度方案计算每个机器负载。 步骤2选择负载最大的机器o。 步骤3随机选择机器o上加工速度不是vd的工序Ojk,并提高其加工速度,其中vd表示工序的最大加工速度。 步骤4计算新个体X′的目标函数值。 (3)NS3 选择负载最大的机器并交换该机器上工序的加工顺序,具体步骤如下: 步骤1从种群中随机选择个体X,根据解码策略生成的调度方案计算每个机器负载。 步骤2选择负载最大的机器o。 步骤3随机选择机器o上两道工序Ojk和Ohz,并交换二者的加工顺序。 步骤4计算新个体X′的目标函数值。 (4)NS4 根据机器的负载量,选择负载最小的机器并降低该机器的加工速度,具体步骤如下: 步骤1从种群中随机选择个体X,根据解码策略生成的调度方案计算每个机器负载。 步骤2选择负载最小的机器o。 步骤3随机选择机器o上的工序Ojk(加工速度为vq′),使机器o用最慢的速度vq加工工序Ojk。若vq′=vq,则重新随机选择工序。 步骤4计算新个体X′的目标函数值。 (5)NS5 选择最后一道工序完工时间为Cmax的机器,并减少该机器上的工序数量,具体步骤如下: 步骤1从种群中随机选择个体X,根据解码策略生成的调度方案。 步骤2选择最后一道工序完工时间为Cmax的机器o。 步骤3随机选择机器o上的工序Ojk。如果工序Ojk所在的工位有多台并行机,则选择同工位的其他机器加工Ojk。如果工序Ojk所在的工位仅有一台机器o,则机器o使用最快的速度加工工序Ojk。 步骤4计算新个体X′的目标函数值。 步骤1输入一个解,根据解码方法生成调度方案,并记录所有工序的开始加工时间和完工时间、所有调整时段的开始时间和结束时间、所有运输时段的开始时间和结束时间等。 步骤2根据调度方案,只有存在空闲时间段的机器才存在降低加工速度的可能性,因此将每个机器的空闲时间段的开始时间和结束时间对放入集合idle,并记录空闲时间段的前一道工序和后一道工序的相关信息。若机器上仅有一道工序Ohz,且其完工时间小于Cmax,则将[ehz,Cmax]时间段加入集合idle。 步骤3根据空闲时间段的开始时间升序排列集合idle中的空闲时段。 步骤5重复执行步骤4,直到空闲时段遍历完毕。 步骤6生成新的调度方案。 以图4所示的个体为例,加入节能算子后所得甘特图如图8所示,该调度方案对应的两个目标函数分别为:Cmax=28.83和TE=260.51。对比图5和图8可知,工序3(3)、3(5)、1(4)和2(6)的加工速度分别从1.5、1.5、2、1.5降为1、1、1和1,在不影响Cmax的前提下,TE减少了13.57,达4.95%。 为验证HMA求解所设计模型的优越性,选取MODE、MOPSO和NSGA-Ⅱ三种常用的多目标优化算法进行对比研究。编程语言为MATLAB,仿真实验在配置为Intel Core i7-10510U CPU @2.30 GHz处理器,16 G内存的计算机上进行。 本文选取CHO等[31]的算例作为实验数据,该算例集共包含120个小规模算例和120个大规模算例,算例集中各参数取值范围如表4所示。 表4 算例集中各参数取值范围 本文分别从小规模问题和大规模问题中随机选择6个用于测试。由于该测试集未涉及调整时间和运输时间的相关参数,假设调整时间约为标准加工时间的20%~60%,运输时间约为标准加工时间的30%~50%。为了便于计算,加工时间和运输时间均取整数,最小值为1。问题规模用(工件数,工位数,重入次数)来表示,如(20,10,1)表示20个工件,10个工位和1次重入的算例。 本文采用IGD和C-metric两个指标来衡量算法的收敛性和解集覆盖率。另外,由于算例的最优Pareto前沿(Optimal Pareto Front, OPF)是未知的,本文使用近似Pareto前沿(Approximate Pareto Front, APF)代替OPF。对于每一个算例,APF通过将所有算法得到的非支配解组合成一个集合,然后从该集合中去除支配解和重复解得到。 反世代距离(Inversed Generational Distance, IGD)是用来评估算法的收敛性和多样性指标。计算公式如式(20)所示: (20) 其中:|N*|为最优Pareto前沿中非劣解的个数,N为算法获取的Pareto非劣解集。IGD值越小,算法的综合性能包括收敛性和分布性能越好。另外,当IGD=0时,N为N*的子集。 C-metric用来衡量两个Pareto解集之间的支配关系。C(A,B)计算过程如式(21)所示: (21) 式中:C(A,B)表示B中的解被A中至少一个解支配的概率,分子表示B中的解被A中至少一个解支配的数量,分母为B中解的数量。C(A,B)=1,说明B中的所有解都被A中的某些解支配;相反,C(A,B)=0说明B中的解没有被A中任何一个解支配。 HMA主要涉及种群规模N、交叉概率Pc、变异概率Pm以及邻域搜索的回退概率Pns四个关键参数。本文采用田口实验设计方法研究关键参数对HMA性能的影响,每个参数的因子水平如表5所示。根据L16(44)直交表,HMA采用直交表中的每个因子水平组合各运行20次。12个算例的支配性指标Ω的平均值表示响应特征值(Response Variable, RV)如表6所示,其中Ω指某种算法的非支配解集同时为OPF的概率,RV值越大,则该实验参数组合性能越好。响应特征平均值(ARV)和每个参数的重要性排序如表7所示。 表5 参数组合 表6 正交矩阵和RV值 表7 ARV和各参数排序 如表7所示,种群规模N对算法的影响最为显著,当N取值很大时会导致算法收敛缓慢并且耗时较长,N取值较小时可能引起早熟收敛而无法取得最优解。邻域搜索的回退概率Pns显著性次之,合适的回退概率Pns可以进一步增强算法的寻优能力,在一定程度上避免算法陷入局部最优。根据实验结果,各因子水平的变化趋势为如图9所示,4个因子的RV值越大表示算法效果越好,因此HMA算法的最优的参数组合为:N=100,Pc=0.7,Pm=0.15和Pns=0.2。为了公平起见,4种算法相同参数取相同值,最大迭代次数设置为100。 为了验证邻域搜索算子的有效性,将HMA与省略邻域搜索的HMA(记作HMA1)进行比较。表8列出了12个算例(每个算例运行20次)的平均C-metric值和置信水平为95%的Wilcoxon符号秩检验得到的p值。 表8 HMA和HMA1算法C-metric指标比较 由表8可知,在所有算例中C(HMA,HMA1)均大于C(HMA1,HMA),因此HMA1算法所获得的非支配解大部分都被HMA算法所获得的非支配解支配,说明本文提出的5种邻域搜索算子有助于提高算法的局部搜索能力。 为了验证节能算子的有效性,随机选择12个算例将HMA与省略节能算子的HMA(记作HMA2)进行了比较。两种算法针对每个算例分别运行20次,表9列出了12个算例的平均C-metric值和置信水平为95%的Wilcoxon符号秩检验得到的p值。 表9 HMA和HMA2算法C-metric指标比较 由表9可知,在所有算例中C(HMA,HMA2)均大于C(HMA2,HMA),表明HMA2算法所获得的非支配解大部分都被HMA算法所获得的非支配解支配。另外,p均小于0.05,说明二者有显著差异且HMA更优。所有算例两个目标值的平均相对变化情况如图10所示,其中负号表示相对减少。相对变化率计算如式(22)和式(23)所示: makespan相对变化率= (22) TE相对变化率= (23) 其中:HMA2avg-makespan和HMAavg-makespan分别表示两种算法所得Pareto解中makespan的平均值,HMA2avg-TE和HMAavg-TE分别表示两种算法所得Pareto解中TE的平均值。从图10可以看出,加入节能算子后,所有案例的TE均有明显降低,部分案例的makespan虽有所增加,但是增加幅度均小于1%,可以忽略不计。因此,本文设计的节能算子在不影响生产效率的前提下,可以大大降低能耗,有助于提高算法的求解能力。 针对每个算例,每种算法独立运行20次,每运行一次得到一组[IGD,C-metric]值。表10和表12分别统计了4种算法运行20次后IGD和C-metric指标平均值。IGD指标的Wilcoxon符号秩检验p值如表11所示,p≤0.05表示HMA与其他算法存在显著差异,且优于其他算法。两个评价指标的箱线图如图11和图12所示,HMA的IGD指标明显小于其他算法,HMA的C-metric指标明显大于其他算法,进一步证明了HMA的优越性。 表10 4种算法IGD指标对比 表11 HMA对比其他算法IGD指标Wilcoxon符号秩检验 表12 HMA与其他3种算法C-metric指标对比 算例Sproblem-04-02和Sproblem-05-02四种算法分别随机运行一次的Pareto前沿如图13和14所示,由图可知,HMA Pareto解的质量要优于其他法。以Sproblem-05-02为例,分析节能算子对调度结果的影响。该算例共有10个工件,6个工位,1次重入以及9台机器,每个工位上并行机器数量分别为2、2、1、1、1和2。以图中A点处可行解为例,两个目标函数值分别为Cmax=92.83和TE=1 790.72,该解对应的甘特图如图15所示。如图16所示为该解在省略节能算子的情况下所得甘特图,两个目标函数值分别为Cmax=92.83和TE=1 998.23。对比可知,在保证生产效率不变的前提下,工序10(2)、4(1)、2(8)、8(1)、9(6)、5(8)、4(3)、 8(3)、7(9)、6(3)、10(5)、1(5)、4(5)以及9(10)的加工速度均有所降低,TE共减少了207.51,达10.38%。为了研究加工能耗、空闲能耗、调整能耗以及运输能耗之间的关系,以图14对应的调度方案为例,4种能耗分布情况如表13所示。对比可知,加入节能算子后加工能耗减少195.9,空闲能耗减少了11.61,其他两种能耗保持不变,再次说明了节能算子的有效性。综上所述,本文提出的HMA和模型能够有效地解决同时考虑调整时间和运输时间约束的绿色可重入混合流水车间调度问题。 表13 加入节能算子前后4种能耗分布情况对比 本文研究了考虑多时间因素的绿色可重入混合流水车间调度问题,以最小化最大完工时间和总能耗为目标建立双目标优化模型,并利用混合文化基因算法(HMA)求解该问题,主要工作如下: (1)结合生产中的实际情况,充分考虑顺序相关调整时间和运输时间等辅助时间特性,并通过调整机器转速手段来实现绿色调度。 (2)针对问题的特性,提出了基于工序,机器和转速的三层编码策略,设计了基于贪婪机器选择和完全随机的种群初始化方法、交叉和变异算子以及5种邻域搜索算子,并且在不改变机器分配和工件排列的前提下,基于降低机器转速手段设计了节能算子,极大地高了算法的寻优能力。 (3)通过实验验证了HMA算法求解GRHFSP-MTF的可行性和优越性。绿色调度广泛存在于实际工业生产中,未来将继续深入研究此类问题,如考虑分布式特征,设备维护与生产调度联合优化,设计更加高效的智能算法等。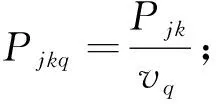
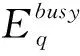
1.3 数学模型
2 改进的混合文化基因算法
2.1 编码
2.2 解码







2.3 种群初始化
2.4 交叉和变异算子

2.5 邻域搜索
2.6 节能算子


3 数值实验
3.1 实验数据
3.2 评价指标
3.3 关键参数设置



3.4 邻域搜索的有效性

3.5 节能算子的有效性

3.6 算法对比实验



4 结束语

