应用长短期记忆循环神经网络的弱反射信号增强方法
隋京坤,陈胜,郑晓东*,胡天跃
(1.北京大学地球与空间科学学院,北京 100871; 2.中国石油勘探开发研究院,北京 100083)
0 引言
由于不同时期沉积地层的岩石性质变化一般较大,形成强反射界面;而同期地层内不同小层的岩石性质变化通常较小,形成弱反射界面。当弱反射界面距强反射界面较近时,地震数据中的弱反射信号往往会被其附近的强反射信号所掩盖,使地震数据的分辨能力降低,导致小层划分困难。
为了识别弱反射界面的地震反射信号,传统方法最常见思路为通过对地震记录进行分解后将强反射界面对应的分量剔除,以突出小层之间界面对应的弱反射信号。匹配追踪算法是研究最多的技术之一,它对信号进行自适应的分解,实现强反射背景的匹配追踪和识别[1-5];子波分解和重构技术[6-12]通过将地震数据分解为不同主频的地震子波集合,将强反射信号对应分量去除后,再进行信号重构,实现去除强反射的目的;基于奇异值分解的波形分解技术[13-15]也是相同的思路,只是信号分解的方法不同;田亚军等[16]提出了采用AIDNN和U-net两个深度神经网络的地震强反射剥离方法。以上方法都要求正确提取地震子波。如果预测的地震子波不准确,“减去法”会存在子波残留,引入虚假的弱信号。Guo等[17]提出使用反Q滤波方法对目标层的弱反射信号和相位进行补偿以增强能量。
近年来,随着计算机性能的大幅提升,神经网络算法被广泛地应用到石油勘探领域。一方面,将机器学习应用到初至拾取[18-20]和层位拾取[21],以提高工作效率;另一方面,由于神经网络强大的拟合能力,避免了求解极其复杂的非线性映射问题,它在地震资料的处理、解释中被广泛应用,尤其是在地震反演[22-25]中。长短期记忆(LSTM)循环神经网络[26]是一种在时间序列分析中得到广泛应用的模型,已经应用于岩相预测[27]、速度谱自动拾取[28]、测井曲线重构[29]、地震数据初至拾取[30]、沉积微相的智能化识别[31]等方面。
针对弱信号增强中“减去法”的局限性,本文提出了一种基于“升弱降强”的新思路。通过对反射系数进行分数次幂运算,获得拟反射系数序列;用原始反射系数和拟反射系数计算合成地震记录和拟合成地震记录,生成训练样本集;然后训练LSTM网络,建立合成地震记录与拟合成地震记录的映射关系;最后将该网络应用于地震数据,增强弱地震反射信号。本文方法不是消除强地震信号,而是通过构建一种幂次反射系数模型缩小弱反射系数与强反射系数的相对差异,从而突出弱反射信号。
1 方法原理
1.1 拟合成地震记录
在地震剖面上,对应强反射界面和弱反射界面的分别是强同相轴和弱同相轴,反射信号能量的大小取决于反射系数的大小及其组合。任意一个地震反射界面的反射系数与地震子波褶积可以得到一个同相轴。当界面相距较近时,弱同相轴被强同相轴掩盖的程度取决于它们振幅绝对值之比,而不是振幅的绝对值。为了减小强、弱同相轴的振幅的比值,本文提出利用分数次幂运算对原始反射系数序列进行重构,得到拟反射系数序列。
设原始反射系数序列为r=(r1,r2,…,rN),拟反射系数序列为R=(R1,R2,…,RN),则
(1)
式中:n=1,2,…,N,N为反射系数个数;j1/j2为分数次幂,其中j1、j2为正整数。
假设反射系数|r1|<|r2|,当幂指数j1/j2<1时,有
(2)
则强、弱反射系数绝对值的比值降低,可以减小强、弱反射系数绝对值之间的差异。当幂指数j1/j2>1时,强、弱反射系数绝对值的比值增大,相对增强了强反射系数。本文应用拟反射系数序列可以对反射系数进行自由缩放。合成地震记录s和拟合成地震记录S可以分别表示为地震子波w与反射系数序列r、拟反射系数序列R的褶积,即

(3)
为保持处理前、后数据的值域的统一性,对合成记录和拟合成地震记录进行标准化处理
(4)
式中:s′、S′分别为标准化后的合成记录和拟合成记录;μs、μS分别为s、S的均值;δs、δS分别为s、S的标准差。
1.2 长短期记忆循环神经网络
循环神经网络(RNN)允许数据在重复网络结构中不断循环,可以让先前步骤中的预测结果加入到当前步骤的运算中,使RNN具备了长期记忆功能。因此,不仅当前步骤的输入会影响RNN的输出,过去所有步骤的输入都会影响RNN的输出。
图1为一个标准的RNN模型,对于给定的序列x=(x1,x2,…,xM)(M为序列长度),RNN可以通过迭代

图1 标准RNN及其展开示意图
ht=tanh(Wxhxt+Whhht+bh)
(5)
给出一个隐藏状态ht。式中:xt为由x分割的第t个子向量;Wxh、Whh分别为输入层、隐藏层的权重系数矩阵;bh为隐藏层的偏置向量。隐藏层以双曲正切函数tanh为激活函数。
RNN存在梯度消失和梯度爆炸问题,因此提出了LSTM网络。LSTM网络除了增加了一个tanh函数层之外,还同时增加了三个门层,即遗忘门、输入门、输出门[32](图2)。
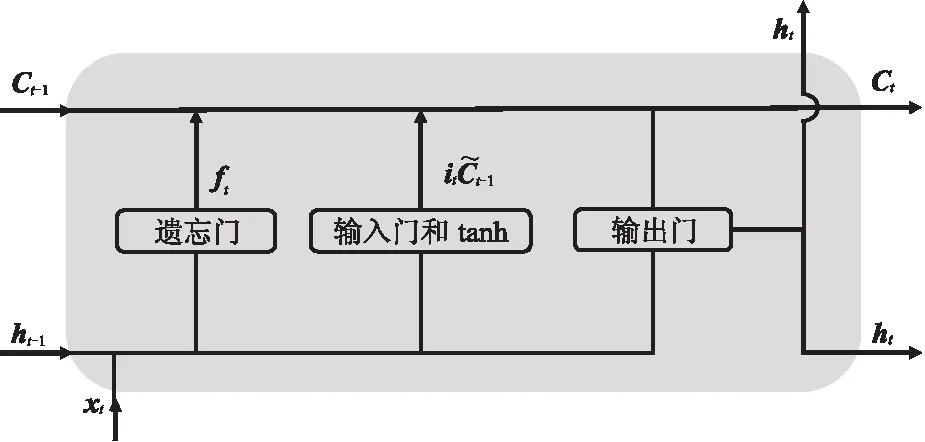
图2 LSTM网络单元结构示意图
遗忘门决定上一时刻的细胞状态Ct-1中哪些被忘记,哪些被保留到当前时刻的细胞状态Ct,遗忘门的状态ft的值域为0~1,可表示为
ft=σ(Wxfxt+Whfht-1+bf)
(6)
式中:Wxf、Whf分别为遗忘门中输入层、隐藏层的权重系数矩阵;σ为Sigmoid激活函数;bf为遗忘门状态f的偏置向量。

(7)
式中:Wxi、Whi分别为输入门中输入层、隐藏层的权重系数矩阵;Wxc、WhC分别为候选更新状态中输入层、隐藏层的权重系数矩阵;bi、bC分别i、C的偏置向量。
当前时刻单元状态Ct的计算式为
(8)
式中“⊙”表示向量中元素按位相乘。
输出门用于将当前细胞状态和它生成的LSTM网络状态输出。输出门的状态和隐藏状态为
(9)
式中:Wxo、Who分别为输出门中输出层、隐藏层的权重系数矩阵;bo为输出门状态o的偏置向量。
1.3 网络训练

X=(x1,x2,…,xL)
(10)
(11)
式中:1≤l≤L;1 (12) 式中:Whp和bp分别为输出单元的权重系数矩阵和偏置;t为1~L之间的整数。与之对应的目标输出为 Y=(y1,y2,…,yL) (13) (14) 与xl对应的拟合成地震记录yl中有N-L+1个数据,预测值只有一个,因此只可以选择数据中的任意1个样点进行拟合,定义为第k(1≤k≤L-1)个样点 (15) 选用均方根误差作为网络的损失函数,定义为 (16) 地震数据服从广义高斯概率分布,但不同数据的值域不同,严重影响LSTM网络的输出结果,因此将输入LSTM网络的地震数据进行标准化 (17) 式中:dn和d′n分别为标准化前、后地震数据d和d′的第n个样点;μd、δd分别为d的均值和标准差。 首先用正演模型(图3a)验证本文算法的可行性。模型宽度为1000 m,道间距为10 m,包含三层,其中中间层的厚度由10 m线性增大到30 m,各层的速度和密度如表1所示。垂直入射情况下,上层与中间层的反射系数为0.05,中间层与下层的反射系数为0.2。本文选用主频为35 Hz的 Ricker子波[33]与反射系数褶积合成地震记录(图3b),两个拟地震记录剖面是地震子波分别与1/2次幂、1/3次幂拟反射系数序列的褶积(图3c、图3d)。为了保证次幂运算前、后数据分布的一致性,需对地震记录进行标准化处理。 图3 模型数据测试结果 表1 模型参数 相邻两道合成地震记录对应的中间层的厚度差为0.2 m。由图3b可以看出,弱反射系数界面对应的同相轴在第75道便无法识别。使用模型反射系数序列的1/2次幂与Ricker子波褶积,其合成记录剖面在第45道就弱到无法识别(图3c)。使用模型反射系数序列的1/3次幂与Ricker子波褶积,其合成记录剖面在第25道才被强反射淹没(图3d)。与原始合成地震记录(图3b)相比,使用拟反射系数序列计算得到的地震合成记录(图3c、图3d)中弱反射同相轴的能量得到增强,分辨率分别提高了6和10 m。 从图3b、图3c的地震剖面中的相同位置选取5道数据分别作为输入数据和标签,制作训练集,其中选取的每次输入的数据长度为40 ms(20个样点),将最终训练结果与标签的均方根误差作为训练集误差。用图3b所示地震剖面作为验证集,将预测结果(图3e)与对应数据(图3c)的均方根误差作为验证集误差。同样对图3b、图3d所示地震剖面进行相同处理,预测结果如图3f所示。对比图3e与图3c、图3f与图3d可见,预测结果与模拟数据的误差极小。 1/2、1/3次幂弱反射增强LSTM网络训练集、验证集误差曲线如图4所示,可以看出式(15)中选用不同的k值(不同采样点)最终计算得到的均方根误差不同,用分割窗口中部对应元素作为标签,拟合误差较小;1/2、1/3次幂LSTM网络的训练集误差相差不大,但后者的验证集误差较大。 图4 模型数据1/2、1/3次幂弱反射增强 工区内目的层地震数据主频为35 Hz,因此将Ricker子波的主频也设定为35 Hz。工区附近有8口井,用7口井的数据制作1/2次幂弱反射增强LSTM网络训练集(图5a),剩下的一口井的数据作为验证集(图5b)。为了防止过拟合,设置当误差小于0.1后停止训练。训练集的均方根误差为0.09,验证集均方根误差为0.21。 图5 测井数据测试结果 图6 四川盆地应用实例 为了进一步展示本文方法的适用性,使用长庆油田X工区地震数据进行测试。该工区具有鲜明的河控三角洲前积反射特征(图7a)。Forest1和Fo-rest2为不同前积期沉积体的分界面。C73为长73底界对应的反射,为该区强反射界面。由于本区相邻的前积体部分区域的的弹性参数差别不大,出现部分区域反射信号弱、同相轴不连续等问题。 相对于原始剖面(图7a),本文方法处理后的地震剖面(图7b)中能量更加均衡,其中强反射信号减弱,弱反射信号明显增强,原本因为反射能量较弱而不能显示的同相轴也突显出来,原先不连续的同相轴更加连续(红色箭头所示),为后期层位拾取提供了可靠的资料基础。 图7 长庆油田实际数据应用 本文提出的基于“升弱降强”思路的分数次幂弱反射增强方法,缩小了弱反射信号与强反射信号的相对差异,避免了“减去法”中强子波残余形成的虚假弱反射。本文使用测井反射系数合成地震记录与拟合成地震记录构建训练集,采用LSTM网络拟合二者的映射关系。模型数据测试表明:LSTM网络模型可以有效地建立合成地震记录与拟合成地震记录之间的映射关系,并且具有泛化能力,可以直接拓展应用于地震数据;避免了直接从地震数据中提取反射系数序列,既减小了计算量,又避免了提取的反射系数误差大的问题。 对于在原始地震剖面中小层界面对应的同相轴难以识别的问题,本文方法可以有效增强弱反射,提高地震数据对弱反射界面的识别能力,为小层划分提供了一种可行方案,有着广泛的应用前景。2 模型实验
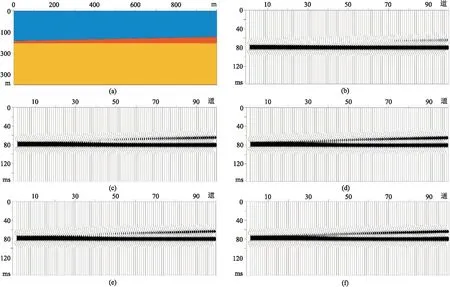

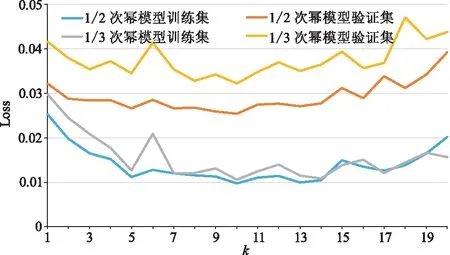
3 实际数据应用
3.1 实例一

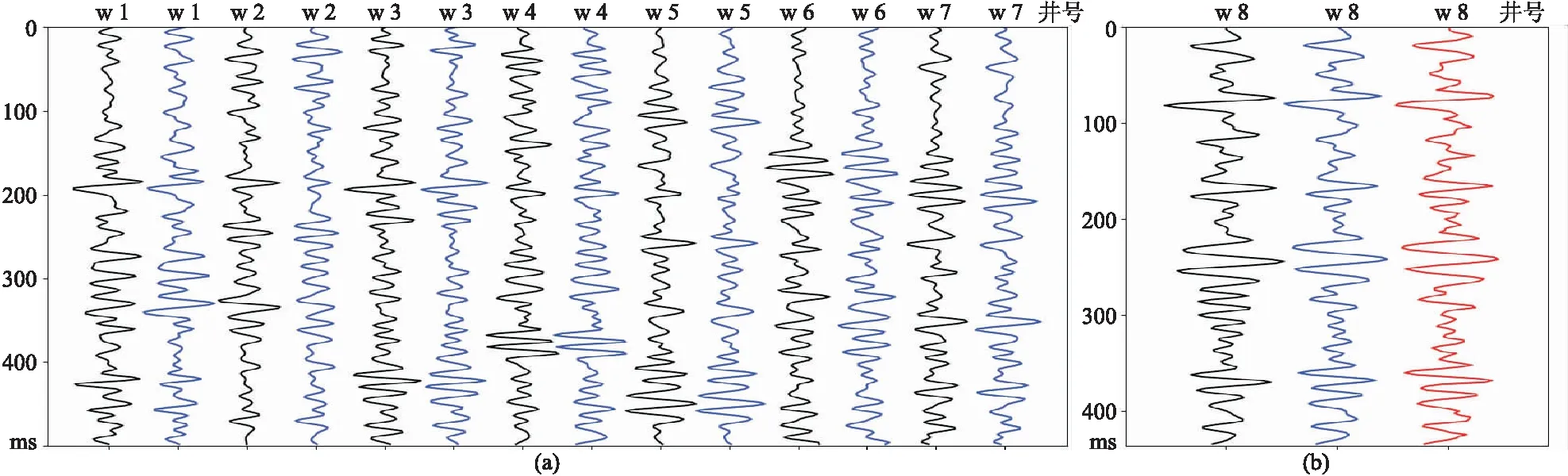


3.2 实例二

4 结束语

