利用先验信息约束的深度学习方法定量预测致密砂岩“甜点”

王迪,张益明，张繁昌，丁继才，牛聪

(1.中海油研究总院有限责任公司，北京 100028； 2.海洋油气勘探国家工程研究中心，北京 100028；3.中国石油大学(华东)地球科学与技术学院，山东青岛 266580)

0 引言

随着石油工业的不断发展，非常规油气已成为当今世界油气勘探的新热点。鄂尔多斯盆地致密砂岩气资源丰富，先后发现了苏里格、米脂、乌审旗、大牛地、神木等5个大气田，勘探、开发潜力巨大[1-2]。由于致密砂岩储层具有低孔、低渗、非均质性强的特征，因此寻找局部发育的高孔、高渗、高饱和度的“甜点”区是取得产能突破的关键。为此，人们研究了“甜点”识别，主要以定性预测为主，其基本思想是通过分析“甜点”储层与非“甜点”储层的岩石物理或地震响应特征的差异，利用反演、属性分析等手段刻画“甜点”展布。张林清等[3]综合应用叠前同时反演、分频属性及属性融合手段，预测西湖凹陷G区致密气储层“甜点”；李岳桐等[4]通过优选敏感特征曲线反演预测细粒沉积岩致密油“甜点”区；李久娣等[5]采用叠前AVO敏感属性技术有效刻画了东海海域深层低渗储层的“甜点”分布；孙文举等[6]依据在三维地震数据体中提取的“甜点”属性与叠前反演得到的泊松比属性，在平面上有效预测天然气“甜点”富集区；韩刚等[7]认为密度参数是识别花港组致密砂岩储层“甜点”的敏感属性，利用叠前AVO三参数反演预测“甜点”；韩飞鹏等[8]优选了表征地质“甜点”区和工程“甜点”区发育特征的5个属性参数，通过融合得到“甜点”分布。此外，有人还定量预测了致密砂岩“甜点”。朱永才等[9]通过多属性优选和非线性回归的方法定量预测致密油孔隙度，刻画了吉木萨尔凹陷芦草沟组“甜点”分布；王迪等[10]构建了适用于致密储层的AVO解释模板，半定量地预测孔隙度和厚度；汪关妹等[11]依据纯砂岩纵波阻抗与孔隙度的数学关系，采用两步法预测致密砂岩孔隙度，进而预测“甜点”储层分布规律；Jaiswal 等[12]利用纵、横波速度建立岩石物理模型，预测了美国俄克拉荷马州脆性“甜点”区；Sreedurga等[13]利用纵波阻抗变化率等多属性分析预测印度巴默盆地致密火山岩储层的孔隙度。目前，针对致密砂岩“甜点”定量预测的研究主要集中在孔隙度方面，有关渗透率、含气饱和度等参数的预测研究很少。

从岩石物理学角度来看，由于储层参数(孔隙度、渗透率、含气饱和度)与地震数据之间并不存在直接的解析关系，无法用显性方程予以描述，导致常规反演等方法无法准确地定量预测“甜点”。深度学习的优势在于通过构建适用的网络模型，能够充分挖掘地震数据与储层参数之间的复杂非线性关系，提高储层参数预测精度[14-17]。丁燕等[18]建立了利用深度信念网络预测潜山碳酸盐岩储层裂缝的方法；杨柳青等[19]利用深度神经网络模型预测储层孔隙度；陈康等[20]基于改进U-Net卷积神经网络预测储层岩性及“甜点”；闫星宇等[21]提出一种用于地震相分类识别的深度学习方法；王俊等[22]基于门控循环单元神经网络预测储层孔、渗、饱参数。深度学习是一种数据驱动的方法，充分的数据和良好的分布是保证预测精度的必要条件。因此，与常规反演方法相比，深度学习对井的数量、质量和分布要求更苛刻。当井数量较少时，由于学习不充分会导致预测结果不可靠[23-24]。LX区块目前已进入开发阶段，钻井数量多且分布较均匀，为开展深度学习奠定了良好的数据基础。实践证明，该区利用深度学习预测储层参数的困难在于地震数据与测井曲线不存在一一对应关系，存在大量矛盾样本，导致常规卷积神经网络难以直接用于井震联合致密储层“甜点”识别。

针对上述问题，本文引入地层格架、地震相等先验约束信息，构建了适用于致密储层的深度学习网络模型，形成了地质导向的样本井优选方法，实现了储层参数高精度定量预测。

1 LX区块概况

LX区块位于鄂尔多斯盆地东缘晋西挠褶带，地理位置横跨山西省临县和兴县(图1)。二叠系石盒子组是主要勘探目的层，发育三角洲平原和前缘分流河道砂体。储层孔隙度为2%～16%、渗透率为0.01～10 mD、含气饱和度为35%～75%。参照GB/T 26979-2011气藏分类标准，该区储层绝大部分属于低孔、低渗储层，少量属于中孔、中渗(孔隙度大于10%，渗透率大于5 mD)[25]储层。

图1 LX区块位置示意图

LX区块钻井结果揭示，优选高孔隙度、高渗透率、高含气饱和度的“甜点”是取得产能突破的关键。通过分析将测试产能数据划分为两组：一组为测试产能大于1万m3/d的井数据，定义为高产井数据；另一组为测试产能小于1万m3/d的井数据，定义为低产井数据。通过对比两者的储层参数(图2)，可知高产井和低产井数据在孔隙度、渗透率、含气饱和度指标上存在明显差异，其中高产井数据具有孔隙度大于12%、渗透率大于1 mD、含气饱和度大于50%的特征。因此，如何准确预测上述三个参数是识别高产“甜点”的关键。

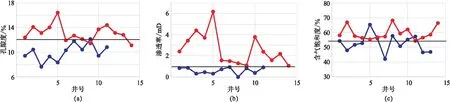
图2 高产井(红色线)和低产井(蓝色线)的地层参数对比

2 技术原理

2.1 矛盾样本问题

样本矛盾是指地震数据与测井数据不是一一对应关系，如地震波形相似、伽马曲线差异很大(图3a)，或伽马曲线均为低值、地震波形差异很大(图3b)。当前流行的深度学习模型无法直接利用井震联合预测致密储层参数。经过进一步分析认为，相互矛盾的样本位于不同的时间和空间位置，即处于不同的层段和地震(沉积)相带内(图4)。因此，可以引入线(道)号、层序格架、地震相等先验信息作为约束，结合地震数据参与网络训练。由于考虑了时间位置、空间位置、波形特征等，样本不再互相矛盾，能够使地震数据与测井数据在相同层段、类似相带内学习与训练，从而提高储层参数预测精度。

图4 样本矛盾解决思路示意图

2.2 网络模型结构

基于上述思想，在常规卷积神经网络模型的基础上增加一个全连接网络结构(图5)。地震数据与测井数据之间通过托布里兹局部网络结构连接，用于解决储层参数与地震数据不直接相关问题。全连接网络结构通过引入线(道)号、层位、地震相等先验信息，可以解决矛盾样本问题。

图5 适用于致密储层的深度学习网络模型结构

基于先验信息约束的深度学习网络模型运算步骤如下。

(1)建立全局连接网络作为深度学习网络的支网一。支网一以地震空间格架信息和其他先验信息作为输入，该结构的每一节点都与上一层的所有节点相连，将地层格架高维特征映射到样本标记空间，层间运算关系为

Yi+1=Wi·Yi

(1)

式中：Yi和Yi+1分别为第i层和第i+1层的输入；Wi为第i层到第i+1层的连接权重矩阵。

(2)建立局部连接的卷积神经网络作为深度学习网络的支网二。支网二以地震数据作为输入，层间运算关系为

(2)

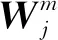
(3)将步骤(1)和步骤(2)的支网运算结果求和，得到总网输出。

网络模型内部结构如图6所示。基于深度学习网络预测致密储层参数的过程如下:

(1)根据LX区块的地质情况，对测井、地震数据进行时深标定；

(2)利用地震层位信息搭建时间域地层格架；

(3)对地震数据进行波形聚类，以划分地震相；

(4)将储层参数训练样本集作为期望输出，井旁地震数据、相应空间格架、地震相信息作为输入，以训练网络；

(5)将靶区地震数据及空间格架信息输入到训练好的网络，得到整个靶区储层参数数据体。

3 样本井筛选

深度学习方法依赖于数据，充分的数据和良好的分布是保证训练精度的必要条件。由于LX区块处于开发阶段，钻井数量多，同一井台上钻探了不同数量的定向井，优选最佳的测井学习样本十分关键。为此，结合LX区块的地质认识，制定了样本井筛选的三个基本原则：①空间分布均匀；②井震标定关系好；③涵盖多种沉积样式和岩性组合。LX区块主要发育河道心滩(图7a)、复合河道(图7b)、河道侧缘(图7c)和分流间湾(图7d)共4种沉积微相及岩性组合，在选择样本井时应尽可能兼顾所有模式。根据上述原则，共筛选26口样本井进行第一轮训练和效果测试。通过测试发现，当同一井台的多口井的钻探结果差异较大时，仅选择其中一口井数据进行学习会引起预测结果的偏差。深度学习效果测试结果表明(图8)：三口井均钻遇中强振幅层位，A-2井钻遇气层(孔隙度高)，A-1和A-3井钻遇干层(孔隙度低，图8a)；只选择A-2井数据参与学习，导致A-1井和A-3井孔隙度预测结果偏高，与钻探结果不符(图8b)；增加A-1井作为样本井，A-3井孔隙度预测结果与实钻结果更吻合(图8c)。因此，在第一轮井位筛选的基础上，补充了16口学习井，以进一步丰富样本的多样性，利用42口井数据训练深度学习网络，从而定量预测储层参数。

图7 LX区块沉积微相及岩性组合模式

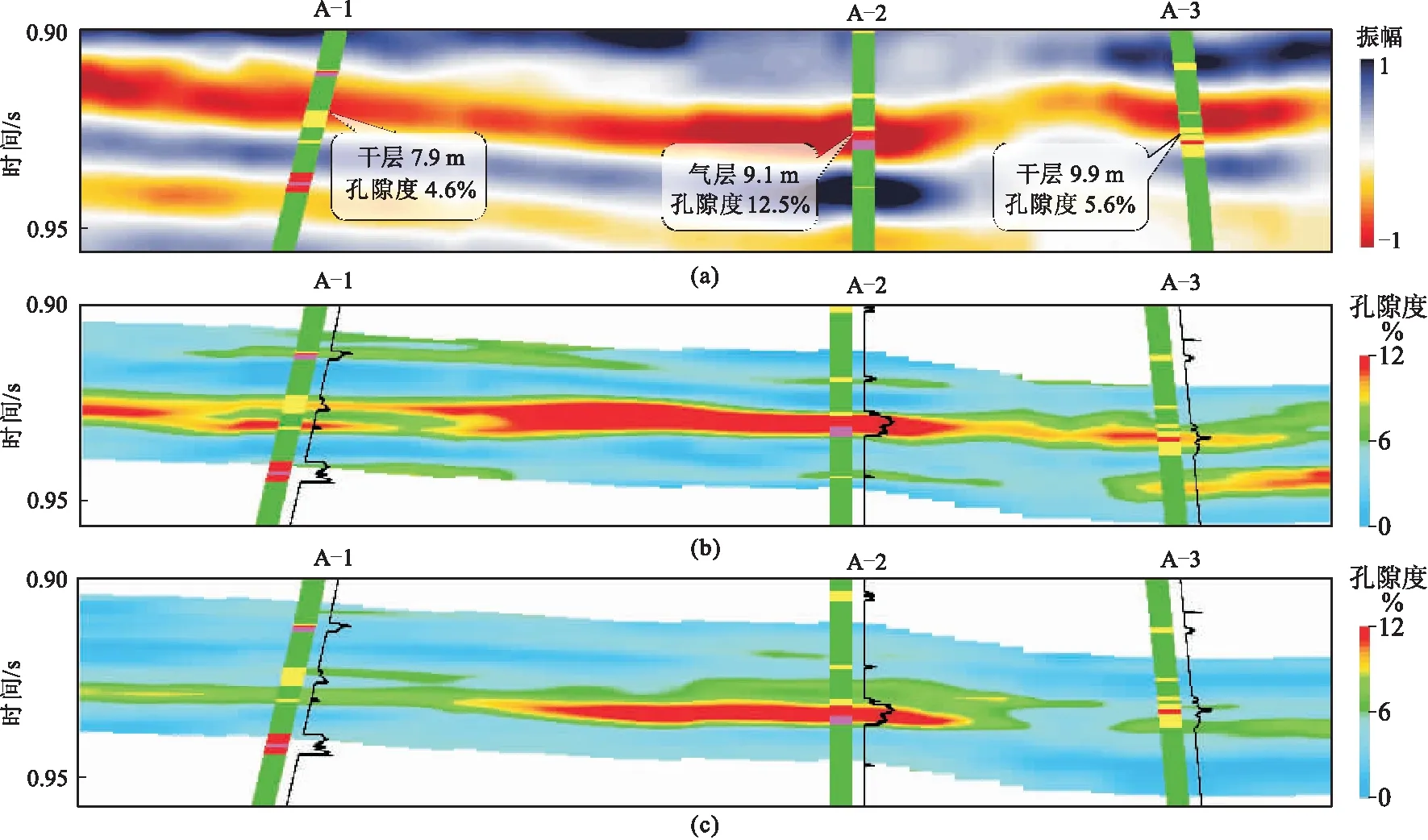
图8 深度学习效果测试

4 应用效果

4.1 储层参数定量预测

图9为不同方法预测的孔隙度剖面。由图可见，与叠前反演间接预测的孔隙度剖面(图9c)相比，本文的深度学习网络预测的孔隙度剖面(图9b)的分辨率更高、连续性更好且与钻井数据吻合度更高，并识别了高孔隙度储层(图中红色椭圆位置)，与测井有效孔隙度曲线更匹配。

图9 不同方法预测的孔隙度剖面

本次深度学习选取42口井数据参与训练，10口井作为验证井分析预测结果的精度。图10为深度学习储层参数预测连井剖面。由图可见，无论训练井还是验证井，预测结果与测井曲线的匹配关系良好，孔隙度(图10a)、渗透率(图10b)和含气饱和度(图10c)剖面的横向变化规律一致。为进一步印证深度学习储层参数预测结果的可靠性，以图10c的四套典型砂体(①～④)为例，对比储层参数预测值与测井实际值(表1)。可见，孔隙度预测相对误差小于10%，渗透率预测相对误差小于18%，含气饱和度预测相对误差小于15%，预测精度较高。

表1 孔隙度、渗透率和含气饱和度预测值与实际值对比

图10 深度学习储层参数预测连井剖面

4.2 高产甜点分布预测

根据深度学习储层参数定量预测结果，考虑到“甜点”(产能大于1万m3/d)对应的参数门槛值(孔隙度大于12%、渗透率大于1 mD、含气饱和度大于50%)，综合孔隙度、渗透率、含气饱和度数据体，刻画了盒四段高产“甜点”平面展布(图11)。可见，叠前反演方法预测的盒四段高产“甜点”呈块状分布(图11a)，与三角洲平原分流河道的地质规律不符。深度学习方法预测的盒四段高产“甜点”具有典型的三角洲分流河道沉积特征，优质砂体呈条带状由北向南展布(图11b)，与沉积规律相符。钻井数据表明：图11a的黑色椭圆区域的“甜点”为异常假象，实际钻井在该区域并未钻遇高产气层；图11b的黑色椭圆区域基本不发育“甜点”，预测结果与钻井数据更吻合。42口井的数据统计结果表明，常规反演方法预测的“甜点”符合率为68%，深度学习方法预测的“甜点”符合率为82%，后者明显提升了预测精度。

图11 盒四段高产“甜点”展布规律预测结果

根据深度学习高产“甜点”预测结果和LX区块内钻井分布，部署了SJ-1～SJ-5共5个有利井位目标，钻探结果如表2所示。由表可见，5口井均钻遇优质气层，实际砂岩的孔隙度、渗透率、含气饱和度数值基本都达到高产“甜点”的储层参数门槛值。其中，SJ-2井的渗透率值(0.89 mD)、SJ-5井的孔隙度值(11.6%)稍低于对应的参数门槛值，存在预测误差。图12为S-4井、S-3井深度学习储层参数预测连井剖面。由图可见，孔隙度(图12b)、含气饱和度(图12c)预测值和实际值吻合度较高。测试结果表明，5口井射孔无阻流量均超过1万m3/d，取得了良好的应用效果，推动了致密气高效开发。

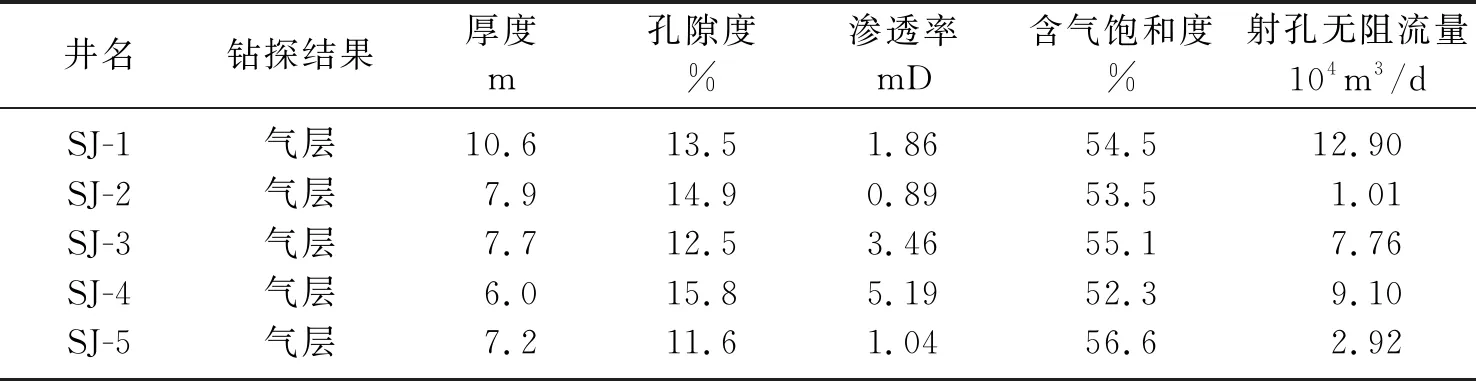
表2 新井钻探结果统计表

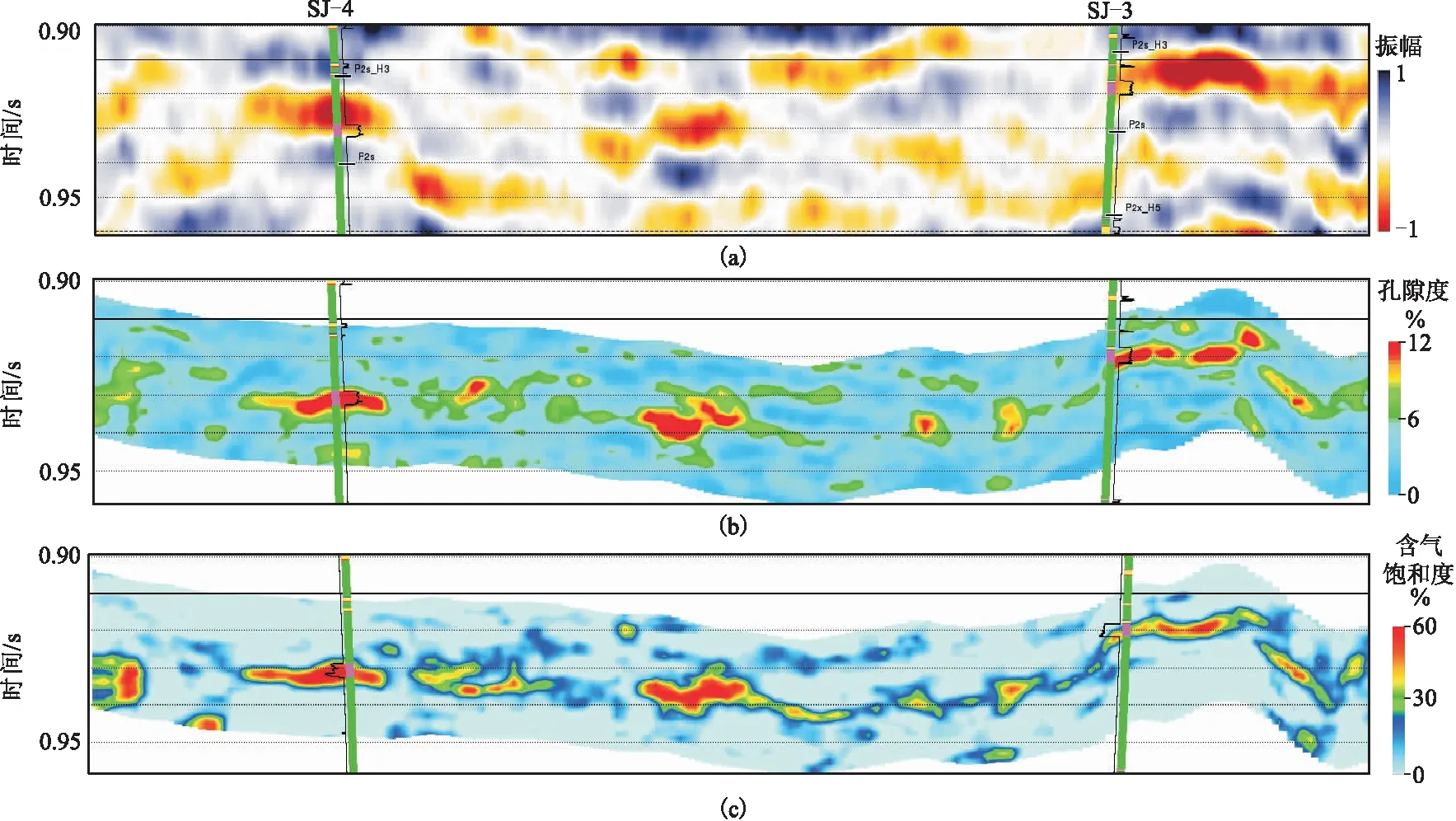
图12 S-4井、S-3井深度学习储层参数预测连井剖面

5 结论

针对现有深度学习模型无法直接预测致密储层的问题，提出了基于先验信息约束的深度学习网络模型，定量预测了储层参数，刻画了高产“甜点”平面展布，指导了开发井位部署，取得了良好的应用效果。该技术主要有以下优势：

(1)将地层格架、地震相等信息作为约束条件加入深度学习网络模型中，解决了矛盾样本的问题，提高了储层参数预测结果的稳定性以及与测井曲线的吻合度；

(2)提出了基于地质导向的样本井筛选方法，能够兼顾各种沉积微相和岩性组合模式，丰富了样本的多样性；

(3)充分发挥测井曲线垂向分辨率高的优势，由井震联合深度学习预测的储层参数结果的垂向分辨率高于地震数据，较好地刻画了致密砂岩储层。