服务差异二级选址路径问题及大邻域搜索算法

杨屹夫，孙 冰，马艳芳，程 聪，冯翠英

1.河北工业大学 经济管理学院，天津 300401

2.浙江工业大学 经贸管理学院，杭州 310014

在电子商务时代，市民既希望所购物品能够快速交付，又能够减少市区的交通拥堵。但随着网购需求的日益增长和客户需求的多样化，给物流公司在以较低成本的条件下保证高效率的物流服务带来了难题。为了实现及时交付并缓解交通拥堵，已经提出了解决“最后一公里”物流问题的方法——设立二级物流设施，以配送点为例，货车先将部分客户的包裹送至配送点，而配送点则通过配送车来为这些客户提供配送服务。而另一种逐渐盛行的方法是设立自助点，特别是在防疫背景下提出的“无接触取送货”，更是促进自助点在物流领域的发展。自助点在物流活动中起到临时仓储的作用，同样是一种二级设施，其一般设立在小区、社区等居住人口密度大的区域，便于客户前往自助点取货，或将物品送至自助点临时存放，等待物流公司取走。客户根据自身情况，结合周围物流设施，提前在网上选择其所需服务类型，而物流公司以此为依据选择开放二级物流设施、规划配送路径，满足客户不同的服务需求。自助点服务可以直接减少配送距离和所需访问的客户，进而有效减低运输、人工、车辆等物流成本。

本文依据客户选择接受的服务类型将客户分为“自取需求型客户”和“配送需求型客户”两类，前一类客户自行前往附近的自助点完成取送货，后一类客户由配送车到达客户点完成取送货。在如此分类下，不仅使得用户不同的服务需求得以满足，还有利于上述问题的解决。本文考虑了设立二级物流设施，并在典型的配送点的基础上进一步引入自助点，构建包含两类二级设施的物流网络，分别服务于不同类型的客户，以物流总成本最小为目标，为物流公司在客户服务差异环境下的服务策略提供支持。

本文研究的是自取需求型客户和配送需求型客户同时存在时的二级配送网络优化问题，目前也有一些文献在客户分类方面进行了研究。郭晓宇等[1]通过建立用户评价体系，用k-means算法将客户按重要度进行分类，对不同类型客户在配送货物提取或延迟中采用不同的策略。夏扬坤等[2]研究了进行客户分级并增加重要客户的时间窗偏离惩罚程度，引导算法求解时优先满足重要客户的时间窗。刘秋萍[3]在配送资源受限的情况下，考虑了客户价值和时间敏感度对客户的服务优先级进行划分，并为不同类型客户设计不同的时间窗约束。黄秋彬[4]同样考虑客户重要度的影响对客户进行分类，建立了物流总成本最小和客户满意度最大的双目标模型，通过M-NSGA-Ⅱ（非支配排序遗传算法）求解，证明了对客户进行分级配送管理的合理性。以上文献通过评估客户价值或重要度来进行客户分类，希望提高物流服务的客户满意度，然而由于评价的过程往往缺乏客观且客户信息不易获取，大多情况下不能达到预期效果，本文按照客户希望接受的物流服务对客户进行分类，直接获取客户需求，更直观地为客户提供所需物流服务。

两级选址-路径问题在近几年也吸引许多学者研究，这类问题一般指的是具有两级物流设施的问题。第一级设施通常指车辆在运输过程中的起点，例如中央配送中心等，第二级设施指在运输过程中的中转站，比如区域配送网点[5]和配送点等。Nguyen等[6]研究2E-LRP的问题，第一层和第二层设施均有容量约束和开放成本，建立了三下标模型，然后通过MS-ILS-PR算法求解。Contardo等[7]针对同样的问题，使用分支-切割法（B&C）和适应性大规模邻域搜索方法（ALNS）求解，并将两种方法进行比较。Schwengerer等[8]为求解该问题，将求解LRP问题的VNS算法进行改进，该算法有7种基本的邻域结构，并结合两种局域搜索算法进行解的改进。Enthoven等[9]对于设置配送点和客户自取点为中转站的2E-VRP-CO问题进行研究，采用改进后的ALNS算法进行求解。关于同时取送货的车辆路径问题（VRPSPD）的研究，最早由Min[10]提出，Dethloff[11]进一步将模型进行完善。李博威等[12]考虑了带软时间窗的同时取送货问题，建立MINLP模型，并采用LINGO对模型进行求解。而更多学者采用启发式算法进行求解，如张烜荧等[13]提出一种超启发式分布估计算法，张庆华等[14]采用模因算法求解，王超等[15]提出一种改进的布谷鸟算法（DCS），并验证了算法的有效性。郭放等[16]考虑设置前置仓进行补存货操作的VRPSPD问题，并设计了一种基于节约算法与自适应大邻域搜索的混合启发式算法CWIGALNS求解问题。目前有关二级选址-路径的文献中缺乏取送货的研究，且已有文献大多只考虑配送成本最低，暂未有文献结合客户服务需求差异进行研究，本文采用在2E-LRP求解上被Enthoven等[9]证明效果较好的ALNS算法求解模型，并对其进行了改进和有效性检验。

综合以上分析，可知已有文献中同时考虑2E-LRP和VRPSPD问题的论文较少，且有关车辆路径问题的客户分类大多从客户重要度的角度出发，暂无按客户服务需求对客户进行分类的车辆路径问题的研究。现有研究主要从VRPSPD的基础问题上增加限制条件或者从提升算法性能方面进行，而缺乏在设置前置配送点、自助点策略以及构建两级配送网络方面的研究。本文考虑了不同配送点的可用配送车数量以及多车型，更加贴合实际情况。总的来说，本文旨在考虑客户不同服务需求的情况下，构建并优化两级同时取送货配送网络来研究城市物流配送服务的问题，并结合了二级设施选址，多类型配送车辆等因素，在已知二级设施拥有的配送车辆情况的条件下，使得配送总成本最小化。总成本包括车辆固定成本、运输成本、自助点与客户点的连接成本、二级设施开放成本。

1 问题描述及数学模型

1.1 问题描述

该问题可以描述为一个多级网络，节点由三层构成，第一层是配送中心，第二层是配送点、自助点，第三层是客户点。第一、二层的节点通过车辆路径进行连接，第二、三层节点通过车辆路径或者自助点服务进行连接，配送中心整理整个区域的订单并通过卡车进行物品转运，将货物运输至各配送点和自助点同时进行回收，这是在一级路径上进行的。商品到达配送点后，物品通过配送车送至客户点，到达自助点后，由客户自取，同时进行回收，这则是通过二级路径和自助点服务来实现。图1为二级选址路径示意图。

图1 服务差异下二级选址-路径示意图Fig.1 Solution for 2E-LRP under different service mode

本文考虑了两类客户所需的不同物流服务，分别是通过配送点和自助点来实现的，配送需求型客户的服务过程是配送员到达客户点后进行取送货，而自取型客户的服务过程是客户自行到达附近的自助点进行物品的存取，按照客户点的需求分类还可将客户点分为三类，取货需求、送货需求、取送货双重需求，这三种类型的需求都可以通过配送点或自助点进行实现，文章后面部分将会以“二级设施”来指代配送点和自助点。

为了构建该配送网络，需要进行三种决策。（1）对二级设施的选址决策：在已有的配送点和自助点集合中，确定提供配送服务的配送点的数量和位置，确定开放的自助点的数量和位置。（2）客户分配决策：决定开放的二级设施为哪些客户进行服务，一位客户只能被分配到一个配送点或自助点。（3）路径决策：确定一级路径上卡车访问二级设施的顺序，以及二级路径上配送车访问客户点的顺序。为了更好地界定问题，本文进行了下述假设：

（1）配送中心的数量是唯一的，且其位置已知，其运输能力足够大，不考虑车辆限制。（2）全部配送点和自助点的位置、待回收量已知，且各配送点拥有的配送车量的数量和类型已知，各自助点的容量已知。（3）各客户点的需求量和待回收量、位置已知。（4）所有物品从配送中心开始配送。（5）客户点、配送点、自助点的需求量不可分。（6）备选配送点和自助点的数目、位置已知，但是否开放需要在求解后确定。（7）物品的配送和回收始终需要经过配送点或自助点转运。（8）一级路径只能使用卡车运输，二级路径表示使用配送车进行取送货，配送车分为大型配送车和小型配送车两类，二者区别于最大载重限制。（9）一级路径必须始于配送中心最后再返回配送中心。二级车辆路径，必须始于配送点，最后再返回同一配送点。（10）选择自助点进行服务的客户，其自行的取送货操作对于一级路径的车辆而言是及时的。（11）在以下情况下客户点只能接受配送服务，一是客户点位于待开放自助点的服务范围之外，二是可以为该客户点通过服务的自助点已到达容量上限。（12）每个客户点只能选择一种服务。

1.2 定义变量

同时取送货网络G=(V,E)，其中V为所有节点的集合，其由J（可选配送点集合）、L（可选的自助点集合）、客户点I和总仓库o构成，其中I={I1,I2}，I1表示配送需求型客户，I2表示自取需求型客户，E:={(vi,vj):vi,vj∈V,vi≠vj}表示连接各节点的弧的集合，E1:={(i,j)∈E|i,j∉I}表示一级运输路径的弧集，E2:=EE1表示二级配送路径的弧集。H、h、Hh都表示车辆集合的映射关系，对于各配送点j而言，映射H(j)表示其拥有的大型配送车集合，h(j)表示其拥有的小型配送车集合，Hh(J)表示全部配送车辆集合，H(o)表示总仓库可以使用的卡车集合。具体变量解释如下。

1.3 数学模型

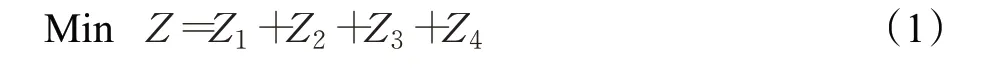
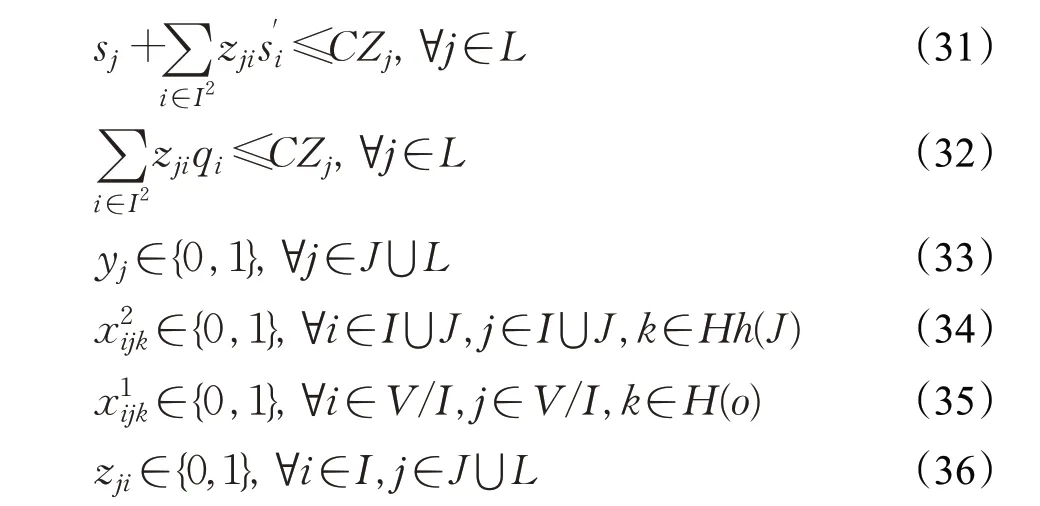
以上模型中，（1）表示最小化总成本，（2）至（5）分别表示各部分成本，（2）表示一、二级车辆固定成本，（3）表示一、二级配送网络的运输成本，（4）表示自助点与自助型客户的连接成本，（5）表示二级设施开放成本。（6）、（7）限制了每个配送点使用的配送车的数量，（8）、（9）分别表示每个配送型客户和配送点的流量守恒约束，（10）、（11）分别保证每辆卡车和配送车的路径起点和终点为同节点，并且每辆卡车或配送车只能出车一次，（12）表示当二级设施被卡车访问时才能开放，（13）至（15）共同保证一位配送型客户只能被一个配送点服务，一位自取型客户只能被一个自助点服务，（16）至（21）表示对于一级路径上运输能力的约束，其中（16）表示卡车访问某二级设施前后载重量的变化，（17）表示所有卡车从总仓库出发时的总载重量为所有客户的需求量，（18）、（19）表示运输过程的连续性，即卡车在运输过程中载重量不变，（20）表示每一辆卡车离开总仓库时的载重量等于其所访问的所有二级设施所服务客户点的需求量，（21）保证卡车在运输过程中的载重量始终不超过最大载重量，（22）至（29）表示对于二级路径上运输能力的约束，其中（22）表示配送车访问一位配送型客户前后载重量的变化，（23）保证每个配送点都需要满足其所服务的客户点的总需求量，（24）、（25）表示配送过程的连续性，（26）、（27）表示每辆配送车从配送点出发时的载重量等于该车辆所访问的配送型客户点的总需求量，（28）、（29）保证配送车在配送过程中的载重量始终不超过最大载重量，（30）表示只有在自助点服务范围内的自取型客户才能被自助点服务，（31）、（32）保证自助点存储的物件量始终不超过其容量。

2 算法设计

ALNS（自适应大邻域搜索算法）是指在迭代过程中，不断地使用多种破坏和修复算子来改进解的质量。其中破坏算子会对解进行一定程度的破坏，修复算子则对破坏后的解进行修复，通过这两种算子复杂的共同作用，对当前解的邻域（破坏、修复算子对对当前解进行操作后得到的解集）进行搜索，寻找更高质量的解，并在迭代一定次数后更新破坏、修复算子对的权重，使得表现良好的算子对有更高的概率被选择。图2为本文设计ALNS算法的具体流程：

图2 ALNS算法流程图Fig.2 Flowchart of ALNS heuristic algorithm

步骤1初始化各种参数，置迭代次数Nc为0，并生成初始解。

步骤2判断是否达到终止条件。若达到则结束算法，输出目前最优解。

步骤3依据“轮盘赌”原则确定本次迭代采用的算子对，然后对当前解进行破坏和修复操作。

步骤4对新得到的解进行评价，通过Metropolis准则以一定概率接受新解，若未被接受则转至步骤7。

步骤5对接受的解进行局部搜索。

步骤6若新的当前解对应目标值优于目前的最优解则更新目前最优解和局部最优解，否则仅更新局部最优解。

步骤7判断是否达到规定更新权重的迭代次数，若达到，则更新算子对权重，并将算子对的调用次数和累计得分清零。

步骤8判断最优解是否连续Ncreset次迭代后仍未更新，若是，则将当前解置为目前最优解。

步骤9Nc=Nc+1，转步骤2。

本文研究的问题以2E-LRPSPD（考虑同时取送货的二级选址-路径问题）为基础，该种问题求解极为复杂，属于NP-hard问题，一般采用启发式算法进行求解。在已有的相关文献[7-9]中，通过实验验证了ALNS对此类问题有良好的求解效果。接下来将会讨论算法的初始化策略、自适应权重、解的接受条件、各种破坏和修复算子、算子对的选择与更新策略以及局部搜索算子。

2.1 初始化策略

在本文设计的ALNS算法中，首先根据贪婪思想在满足载重约束的条件下生成初始解，贪婪初始化算法步骤如下：

步骤1选择距离配送点最近的客户，将其插入该配送点的配送路径中，构建路径(j,i,j)为当前配送路径，其中j为配送点，更新待插入客户集合。

步骤2当前配送路径下，依次遍历每位待插入客户的每一个插入位置，并计算出该客户的最佳插入位置和对应的最小插入成本，按照每个待插入客户点的最小插入成本将客户升序排序。ck=dik+dkj-dij表示待插入客户k在当前二级路径上的节点(i,j)之间进行插入的成本。

步骤3从排序最靠前的待插入客户开始，尝试将其插入至当前路径的最佳插入位置中，插入后若新路径违背载重限制，则将其删除后继续尝试下一位待插入客户，直到能够有一位客户完成插入。若始终无客户可插入，则转至步骤5。

步骤4更新待插入客户集合和当前配送路径，判断待插入客户集合是否为空，若是空集，则转至步骤6，若不是，则转至步骤2。

步骤5在待插入客户集合中选择距离配送点最近的客户，同时按照各配送点与该客户点的距离为指标将各配送点进行升序排序。从排名最前的配送点开始，依次检查配送点是否存在闲余的配送车能够进行配送，若存在，则构造一条新路径，然后更新当前路径和待插入客户集合，再转至步骤2。

步骤6定义可以为自取需求型客户i提供服务的自助点集合U(i)，以客户点与U(i)中最近自助点的距离为指标将客户点进行升序排序，按此顺序依次安置客户。

步骤7依次遍历客户点，依次安排U中距离较短的自助点对其进行服务，若满足容量约束，则将该客户点安置到相应自助点，直到遍历完所有客户点，算法结束。

2.2 自适应权重

每进行完一定的迭代次数ϕ后，需要更新算子对的权重，整个迭代过程可以据此被划分为几个阶段。依据该算子对的调用次数ldr以及在前一阶段累计的分数scdr更新权重。在第一阶段每个算子对的权重都设为1，且每次更新完权重后，将ldr和sdr清零。

破坏、修复算子对(d,r)对应的累计分数scdr的累计方式根据该算子对在上一阶段中的表现情况而定，具体而言，当采用该算子对进行迭代后，得到的解对全局最优解进行更新，对scdr累加σ1；当得到的解对局部最优解进行更新，则对scdr累加σ2；当得到的解比局部最优解差，但是仍被接受，则对sdr累加σ3，累加分数的大小满足σ1＞σ2＞σ3≥0。

更新算子对(d,r)对应权重wdr的具体方式如下，其中ρ∈[0,1]为衡量算子对表现情况和其更新前权重的重要度因子，当其值取0时，算子对的权重会一直在初始水平保持不变，当其值取1时，算子对的权重更新仅依赖于其上一阶段的表现，所以取0＜ρ＜1才能同时对两方面进行考虑。

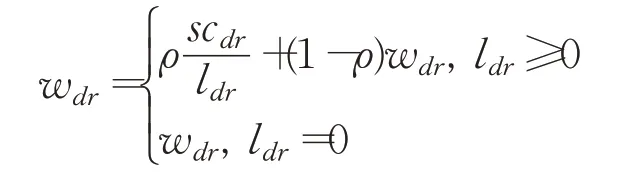
2.3 退火条件

当寻找到一个新解时，需要判断其是否被接受，若该解优于局部最优解，则接受该解，否则按照下面这个准则进行判断：以概率p=(exp(F(s)-F(s′))/T)接受较劣解，其中F(s′)是较差新解对应的目标值。这种依概率接受较劣解的方法与模拟退火中的Metropolis准则相同，其中初始温度[17]设置为，设置φ1=0.03，φ2=0.5。降温过程为

2.4 相关算子设计

2.4.1 破坏算子

在算法迭代过程中，首先需要对当前解进行“破坏”操作，即从现有解中移除q个单位的客户。一般的做法是，对当前已经被安置到二级设施的客户，计算出一种特别的排序指标，对这些客户进行排序，最后根据排序依次将客户移除至集合R中，直到移除了q位客户为止。下面所称的“客户”若无特别说明则指代全部客户。以下是算法中采用的七种破坏算子。

RaR：该算子随机指定客户进行移除操作，这种破坏算子由于没有借助任何信息，所以往往产生一组不太好的被移除客户，但是这种随机移除的方法有助于搜索到多样化的解并脱离局部最优。

RDR：首先随机地产生一位待移除客户，然后计算其余客户与该客户的关联度指标，关联度考虑的是两客户点之间的距离的接近程度dij。

WCR：该破坏算子移除对于整个目标值影响最大的那些客户点，并希望能够找到更好的插入位置，进行移除操作所依据的指标是“对目标值的贡献度”，计算式为Jk=F(s)-F(s-k)，其中s-k为去除客户k后的解。

RoR：任意选择一条配送路径上的客户进行移除，直到移除q位客户为止。

SBR：任意选择一个二级设施，然后随机地选择该配送点提供服务的客户进行移除，直到移除q位客户为止。

ARR：按照所有自取型客户对应的(|U|-1)为指标，采用“轮盘赌”原则选择客户点进行移除，直到移除q位客户为止。

SPR[16]：随机地选择两个同类型的二级设施，随机移除两个设施之间矩形区域内的同一类型客户点，直到达到规定数量为止。

2.4.2 修复算子

修复算子根据被移除的客户集合R以及被破坏后的解进行修复操作，在客户点插入后均需检查是否满足约束。以下是算法中采用的五种修复算子。

RGI：随机生成待插入客户顺序，依次对客户进行下述操作，对于客户点k，遍历每一个可行的插入位置，并计算出插入成本，选择插入成本最小的位置进行插入，插入成本主要考虑插入后所增加的配送距离或者连接成本，下面为计算配送需求型客户插入成本的方法，其中i和j是进行插入前相邻的两个节点，u(i,k,j)表示客户点k插入i和j之间产生的插入成本。

对于自取型需求客户，则按照下式选择自助点。

BGI：遍历每一位待插入客户，计算出其最佳插入位置和对应的最小插入成本，然后选择所有客户中插入成本最小的客户以及插入位置，进行插入操作。计算式如下：

对于自取型需求客户，则按照下式选择自助点。

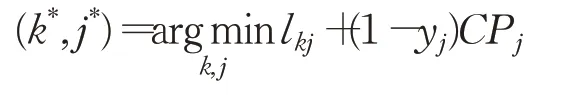
NGI：在RGI计算插入成本的基础上乘以干扰因子τ得到新的插入成本，干扰因子的取值为区间[1-λ,1+λ]内服从均匀分布的随机数，设置λ=0.25。

RaI：随机插入，只要插入后的解满足约束即可进行插入。

BRI：后悔插入，首先按照后悔值指标对待插入客户进行排序，然后依次将客户插入至最佳可行位置。对于配送需求型客户，后悔值的计算式为uk=dk2j-dk1i，其中dk1i是待插入客户点距离未被移除客户点的最小距离，dk2j是次小距离。对于自取需求型客户而言，uk=+(1-yj)CPj-lk1i-(1-yi)CPi，其中i为使得插入成本最小的自助点，j为使得成本第二小的自助点。按照后悔值不减的顺序依次进插入客户，对于配送需求型客户，首先找到距离该待插入客户最近的未被移除的客户点，选择此客户点左右位置中使得目标值增加较小的位置进行插入，若都不可行则选择距离次近的未被移除的客户点，选择其左右位置尝试插入，直到该待插入客户点安置完毕若始终无法插入则开启一条新的配送路径，将客户点安置其中。对于自取需求型客户，在符合容量约束的前提下，选择使得插入成本最小的自助点。

2.4.3 选择破坏/修复算子对

在算法迭代过程中，有多种破坏和修复算子的组合对可以选择，本文采用轮盘赌的原理进行算子对的选择，具体做法是先依据不同算子对在过去的表现情况赋予其不同的权重，然后在此权重下根据轮盘赌法则进行选择。一般而言，一个算子对在过去的表现情况越好，其对应权重也就越大。对于选择某一个算子对的概率pdr，其计算式为：

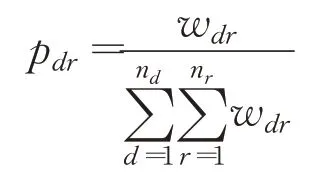
2.4.4 局部搜索算子

如果当前解满足接受条件，就会对当前解进行局部搜索，每进行一次局部搜索都会依次尝试五种算子，顺序是Inter_2-opt、Inter_swap、Inter_0-1exchange、Intra_swap、Intra_shift。前三种算子是径内搜索，后两种是径间搜索，只有当改变后解的目标值优于当前解的目标值时，才会将当前解替换。采用局部搜索时，首先是对二级路径进行优化，而后对一级路径进行优化。Inter_2-opt[18]的操作是随机选择路径（一级路径或二级路径），然后随机选择路径上的两节点，对包括两节点在内以及两节点之间的所有节点进行逆序操作。Inter_swap的操作是随机选择路径上两节点进行交换。Inter_0-1exchange的操作是随机选择一个节点插入到该路径上的其他位置。Intra_swap的操作是交换两个路径上的两个节点。Intra_shift的操作是将一条路径上的一个节点插入到另一条路径上。

3 基准案例分析

本章首先说明ALNS算法的参数设置，而后为验证算法的性能，对经典2E-LRP案例——Nguyen数据集进行求解，然后将结果同另外三种算法以及BKS（best known solution）进行对比。接下来选择两个基准案例进行算法收敛性分析。最后介绍模拟数据集并进行结果分析。实验计算机的配置为2.60 GHz Intel Core i5-7300U处理器，编程环境编写为Matlab2019a，操作系统为Windows 10 64位。

3.1 算法参数设置

本文设计的ALNS算法主要涉及的参数除了在第2章中提到的外，还包括最大迭代次数Ncmax，权重因子ρ，两次更新算子对权重的间隔迭代次数ϕ，破坏算子移除客户数量服从离散均匀分布，并设定在连续迭代Ncreset次后若仍未更新最优解，则重新从目前找到的最优解处开始搜索。通过进行一定的算法测试和文献参考[9，17]，算法参数设置如表1所示。

表1 算法参数Table 1 ALNS heuristic parameter tuning

3.2 算法对比分析

为了进一步验证算法的有效性，采用参考文献[6]中使用的Nguyen算例，该算例是2E-LRP问题的国际通用算例，包含24个测试算例，每个算例均有1个配送中心，有5个或10个中转配送点，25至200个客户点，算例可以表示为n-m{N,MN}，n表示客户点数，m表示配送点数，N表示客户点呈正态分布，MN表示客户点呈高维正态分布，该算例的物流成本由运输成本、车辆固定成本、二级设施开放成本组成。本文选取客点为{25，50}的测试算例，通过ALNS对每个算例进行5次求解，记录求得的最优解和目标值，并将求解结果与BKS[5]、GRASP-LP算法[5]、GRASP-LP-PR算法[6]、H4+VND2算法[6]做比较，结果如表2所示。

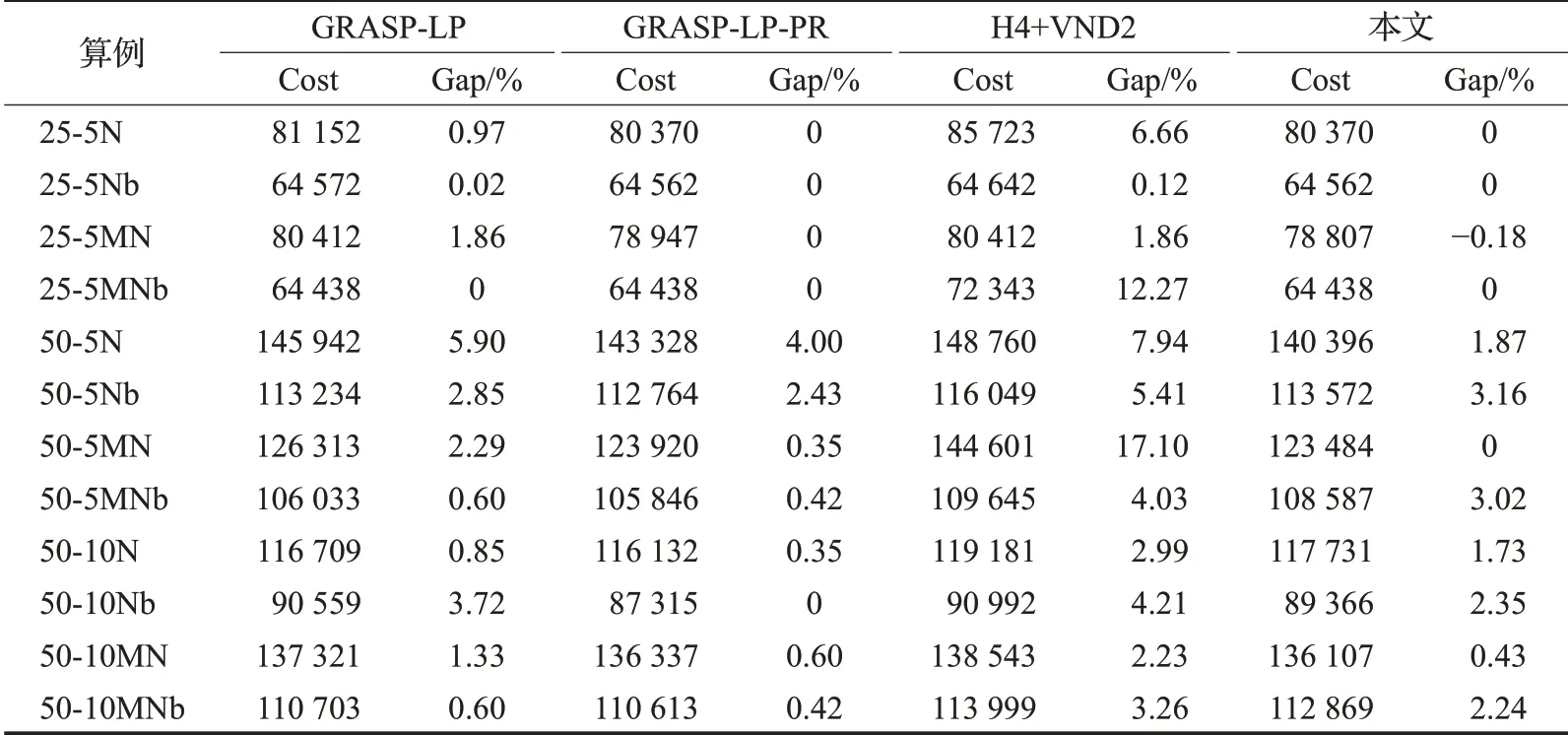
表2 不同算法求解Nguyen数据集的结果Table 2 Results comparisons for Nguyen instances

本文设计的ALNS算法在客户规模为25的算例中更新了1个算例的目前最优解，其余和最优解相同，在客户规模为50的算例中，均接近或达到最优解。采用Gap值（由算法求解结果与BKS的差距除以BKS得到）衡量算法求解结果。所有算例求解的平均Gap值为1.22%，可见对于小规模客户的算例，该算法能够得到较好的求解结果，算法性能明显优于GRASP-LP（Gap均值为1.75%）和H4+VND2（Gap均值为5.67%）算法，由此可以证明ALNS算法解决2E-LRP的有效性。

3.3 算法收敛性分析

为进一步验证ALNS算法求解2E-LRP问题的有效性，确保算法的求解结果可以收敛到较好水平，选取Nguyen数据集中的50-5Nb、50-10Nb两个算例进行求解并记录每次迭代的目标值绘制出迭代图以验证算法收敛性能。

从图3可以看出目标值在100代以内迅速下降，在200～300代的迭代过程中缓慢下降，50-5Nb算例在250代附近收敛于最优结果，而50-10Nb算例在500～750代中仍有缓慢下降的趋势，在750代左右收敛至最优结果，这是由于50-10Nb算例的解空间更大。

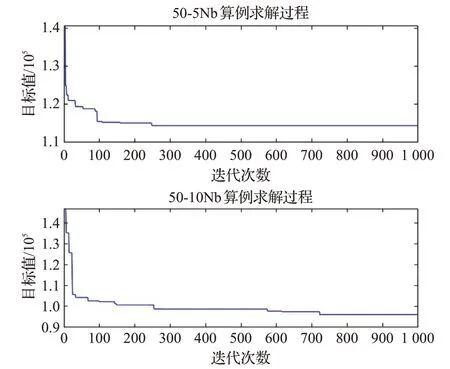
图3 两个基准案例收敛曲线Fig.3 Convergence curves of two classic instances

4 实际案例模拟

4.1 模拟数据

本文设计的案例有1个配送中心、5个待开放配送点、10个待开放自助点、75位客户，其中含50位配送需求型客户和25位自取需求型客户，由于版面限制，表3只列出15位客户的相关信息，其中“配送需求型”客户的客户类型为1，“自取需求型”的客户类型为0。配送中心和二级设施的信息如表4所示。

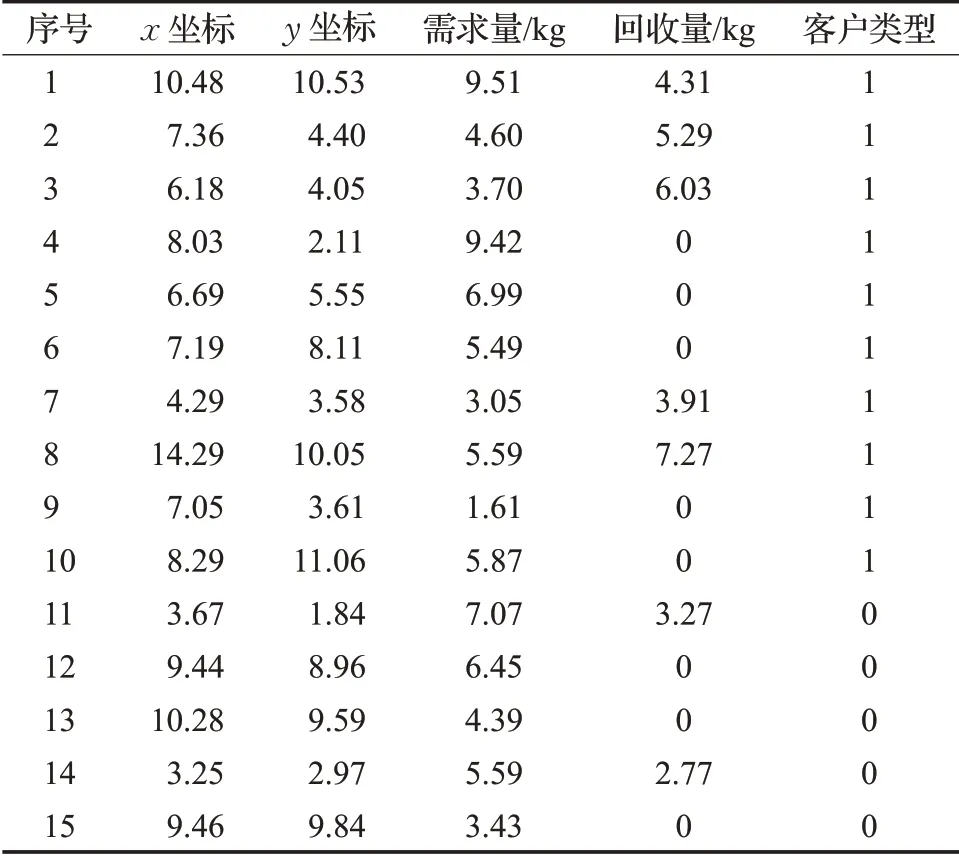
表3 部分客户信息表Table 3 Information sheet for some customers

表4 物流设施信息表Table 4 Information sheet for logistics facilities

本案例中包括的模型参数通过参考实际资料和相关文献[5-7，9，18]来进行设计。其中客户点的坐标位置呈二维正态分布，需求量和待回收量呈正态分布，考虑到在实际情况下存在待回收量的客户数量要少于存在需求量的客户数量，故案例中存在待回收量的客户数量占客户总数的53.3%。

考虑到物流服务的便利性，配送点和自助点这类二级设施一般设置在靠近客户点处。本案例中的一级物流设施是配送中心，数量为1，且位置已知，一级路径配送车辆无数量限制。每个二级设施对应不同的开放成本和待回收量，其中每个配送点的可调用配送车数量如表4最后一列所示，斜杠左侧表示可调用小型配送车数量，右侧表示可调用大型配送车数量。

其余模型参数设置如下：一级车辆容量是600 kg，二级车辆中，小型配送车容量是30 kg，大型配送车容量是50 kg，一级车辆的固定成本是100元，小型配送车为20元，大型配送车为40元，车辆每千米运输费用是1元。自助点的容量上限均为40 kg，服务范围半径均为2 km，每千米的连接成本为0.5元。

4.2 模型结果分析

基于以上数据，运行ALNS算法10次，最优的求解结果如下，其中0代表配送中心，负数代表二级设施，-1至-5依次代表1号至5号配送点，-6至-15依次代表1号至10号自助点。

选址决策：配送点-1，-4，自助点-7，-8，-10，-11，-12，-13

一级路径：

0➝-6➝-2➝-10➝-13➝-14➝-12➝-4➝-11➝-8➝-1➝-7➝0

二级路径：

-1➝3➝46➝31➝35➝6➝11➝10➝34➝-1（大型配送车）

-1➝47➝2➝20➝5➝50➝-1（小型配送车）

-1➝26➝28➝44➝7➝29➝40➝27➝36➝12➝4➝9➝-1（大型配送车）

-4➝23➝18➝16➝42➝19➝15➝8➝14➝21➝49➝37➝48➝-4（大型配送车）

-4➝39➝24➝17➝45➝22➝1➝32➝38➝-4（大型配送车）

-4➝25➝30➝33➝13➝41➝43➝-4（小型配送车）

自助点服务：

2号自助点（-7）：51，54，58，61，68，69

3号自助点（-8）：57，60，62，74

5号自助点（-10）：53，55，56，59，63，65，71，75

6号自助点（-11）：52，70，72

7号自助点（-12）：66，67

8号自助点（-13）：64，73

由此可知，物流总成本1 693.89元，包括车辆固定成本300.00元，运输成本115.72元，连接成本28.17元，开放成本1 250.00元。

从结果可以看出，只开放2个配送点，但一级车辆访问了3个配送点，这是由于部分配送点存在待回收量而不提供服务，自助点同理。共调用6辆配送车，而其余3个配送点的配送车均为闲置状态，开放配送点配送车的使用率均达100%。开放6个自助点，但自助点的服务客户数量差距较大，有的自助点服务8位客户，接近容量上限，而有的自助点只服务2位客户，还有较多的剩余容量，这是由于自助点的位置不同，在客户点密集处的自助点往往有较大服务率，因此应该在这些自助点附近增设一些自助点，而服务客户少的自助点往往位于客户点疏散的区域，若配送点离该区域较远，可以考虑设置自助点来对该区域客户进行服务，以缩短配送距离。

表5对比了“单一配送服务模式”和“存在服务差异的配送模式”的各项成本，前者的结果是将自取需求型客户转化成配送需求型客户后，运行算法5次所得到的最优结果。可以看出前者的总成本比后者高出10%左右，其中运输成本增幅最大达43%，车辆固定成本增长约33%，开放成本增长约4%，可见提供差异化的客户服务可以有效减少运输成本和车辆固定成本，从而降低总物流成本。

表5 两种服务模式的比较Table 5 Comparison of two service modes

总的来说，通过不同的服务方式满足客户取送货需求的配送模式不仅有利于减少配送路径的距离和使用的配送车数量进而降低成本，还有助于减少规划配送路径的时间和难度的同时满足客户不同的服务需求。

4.3 模型灵敏度分析

为了考察模型参数对求解结果的影响，选择重要参数小/大型配送车载重量Q1/Q2，客户需求量d，自助点容量上限CZ，自助点服务半径r，进行灵敏度分析。以4.1节设置的模型参数为基准值，将Q1/Q2、d、CZ、r的基准值依次增加+10%、+5%、0%，-5%、-10%，某一参数改变时，其余参数则保持在基准值不变，每次模型参数变化，运行算法5次，记录平均求解结果和标准差，结果如表6所示。

表6 模型参数灵敏度分析Table 6 Sensitivity analysis of model parameters

配送车辆载重Q1/Q2与物流总成本呈现负相关，即车辆载重限制越大，则物流成本越小，且模型结果对该参数取值较为敏感。在满足所有客户点的需求的前提下，客户需求与物流成本同样呈正相关，总成本对该参数较为敏感。自助点的容量CZ和服务半径r与总成本呈负相关，当自助点的容量增加10%时，成本会有明显的下降，服务半径增大时，物流成本的波动性会有明显的增大。因此，决策者可以考虑增加自助点的容量、服务范围，或者提高配送车量的载重上限，进而减少总物流成本。

4.4 实际案例算法对比

为进一步验证自适应大邻域算法的有效性，依次采用基本遗传算法、蚁群算法、粒子群算法对实际案例进行求解，每种算法运行10次，记录每次运行的结果，得到平均求解结果和最佳求解结果，再计算每种算法最佳结果与ALNS算法最佳结果的Gap值。

从表7可以看出，ALNS对案例的求解结果优于三种基本经典启发式算法，其中GA与ALNS算法的最佳结果最为接近，二者的总成本相差4.99%，而后是ACO（总成本相差6.35%），最后是PSO（总成本相差8.76%）。因此，本文设计的ALNS算法求解服务差异下的二级选址-路径问题有良好效果。

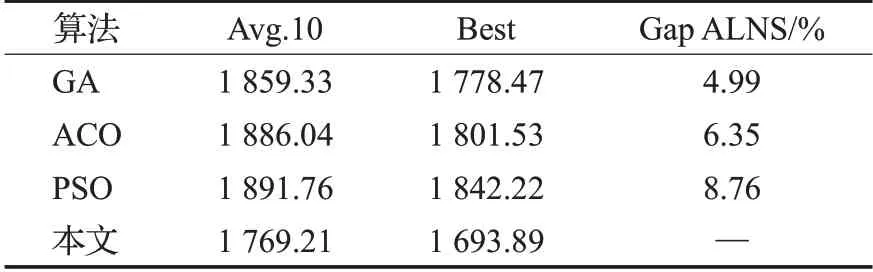
表7 三种经典算法与ALNS的对比Table 7 Comparison between three classical algorithms and ALNS

5 结束语

本文研究了在客户存在不同服务需求的情况下的二级选址-路径问题，将客户分为配送需求型和自取需求型两类，通过开放配送点和自助点两种二级物流设施来满足不同客户的取送货需求。进而根据问题设计了一种有效的自适应大邻域算法，并使用2E-LRP的Nguyen算例进行测试，与GRASP-LP、GRASP-LP-PR、H4+VND2算法所求结果进行比较，并在25-5MN算例中更新了已知最优解，而在其他算例中达到或接近最优解。同时将ALNS与三种经典启发式算法进行对比，验证了ALNS算法求解问题的有效性。

本文研究为存在自取需求型客户和配送需求型客户的物流企业提供了理论模型和算法支持，保证有效地进行二级设施选址决策和两级路径决策和自助点的服务决策，以达到降低物流成本和满足客户需求的目的。

下一步仍继续对该配送模式进行研究，考虑拥有双重需求用户的取货、送货需求由不同的二级设施进行满足的情况，并考虑不确定服务类型的客户，通过算法求解得到合理的服务方式，还可以探究客户接受某种服务的柔性，即可以以一定代价将客户接受服务类型改变，以便近一步降低成本费用。