基于数据挖掘的ETC门架系统多维数据融合应用

李 锐

（安徽省高速公路联网运营有限公司,安徽 合肥 230000）

0 引言

高速公路车辆行驶路径预测的结果可用于运输组织优化、异常行驶路径分析、交通状况预测、交通热点分布分析等，对高速公路交通管控有着十分重要的意义。[1]在高速公路门架系统建设前，对于环网造成的多义路径问题，采用在入口和出口中间建设标识点的方式来精确识别和预测行驶路径。2019年启动取消高速公路省界收费站工程后，通过路网增设的近29 000 套ETC 门架系统，可以更加精确地实现路径识别，并从ETC 收费系统中的入口、出口、门架、车道、时间、车牌、车型等数据中，挖掘出具有一定特征的车辆在一定行驶行为和行驶状态下的行驶规律，从而预测出车辆后续的行经门架，分析异常行驶路径。[2]该文通过对ETC 门架数据的挖掘，构建了ETC 门架序列数据库，并在此基础上实现了单一马尔可夫链，并给出了转移概率的计算方法。针对单一马尔可夫链在预测上准确率和覆盖率不足的缺点，提出了多维融合的马尔可夫路径预测模型，该模型在单一马尔可夫链的基础上，将门架系统数据中得到的时间维、路网维、车辆维数据进行多维融合和信息下钻，预测出车辆的在途后续行驶路径。

1 路径预测模型

自1959年车辆行驶路径问题被提出以来，很多算法和数据模型用于解决行驶路径计算和预测问题。启发式算法中的禁忌搜索算法、遗传算法和模拟退火算法实现了全局最优解的功能，多用于解决最短路径问题；蚁群算法虽然用于解决旅行商问题，但是容易陷入局部优化的缺陷，不适用路网规模较大的情况；卡尔曼滤波法基于车辆运动模式，对车辆未来行驶路径进行预测，也用于道路交通量的预测；固定阶马尔可夫模型则可用于短距离路径预测。

根据《高速公路ETC 门架系统技术要求》布设原则，ETC 门架与互通立交、入/出口匝道端部、被交道路直线距离1.5～3 km，相邻两个实体门架间的平均里程约为15 km。如果能够通过车辆数据、路网数据、时间数据的融合挖掘，预测车辆即将行驶的下一个或下几个门架，则实现了动态预测车辆行驶路径的目的。因此，在当前被ETC 门架全覆盖的路网环境下，更适宜采用马尔可夫模型进行短距离路径预测。

2 基于ETC 门架序列的单一马尔可夫链

2.1 联合概率分布

马尔可夫模型是基于当前状态仅仅依赖于前几个状态的马尔可夫假设来实现的。n阶马尔可夫模型的意思表示是：状态间的转移仅依赖于前n个状态的过程。将车辆从某个门架开往下一个门架的动作表示为该门架的状态转移，该门架到达下一个门架的概率为转移概率。则根据一阶马尔可夫链，车辆经过某个门架序列的N次观测序列的联合概率分布为：

式中，p(xi)——车辆开往门架i的观测概率；——车辆开往门架n的概率观测值，该值仅依赖于车辆经过门架n-1 的观测概率。由此可知，由前n个状态决定的n阶马尔可夫链公式表示如下：

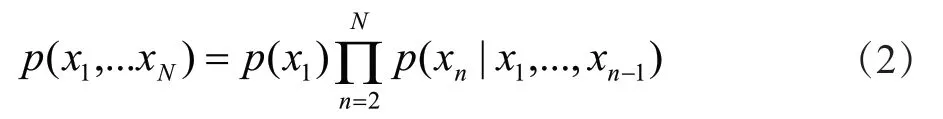
2.2 ETC 门架序列数据库

为了能够基于马尔可夫模型计算出车辆经过某个门架序列的概率，需要建立ETC 门架序列数据库，实现对路网中所有路径的数据化表示，并供路径预测模型调用。门架序列可以是单个门架，也可以是多个转移概率为100%所组成的序列。

假设ETC 车辆在高速公路上所经过的门架为一个门架序列，则车辆所经过的门架序列构成ETC 门架序列数据库GSDB，表示为：

GSDB={x1,x2, …,xm}，其中xi(i=1…m)表示车辆行经的门架序列。

2.3 GSDB 单一马尔可夫链

GSDB 马尔可夫链表示为：M=。

X是GSDB 的集合，可表示为{x1,x2, …,xn}，每个xi对应一个门架序列{x1,x2, …,xm}，称为模型的一个状态；

P为转移概率矩阵，P=pij=p(Xt=xi|Xt-1=xi)表示由状态xi转移到状态xj的概率。

P满足以下条件：

2.4 基于GSDB 的单一马尔可夫链的路径预测

假设某辆车在t时刻生成的车辆路径序列为x，状态用xt表示，则t时刻处于状态xi的第i维等于1, 其余各维都为0。则基于GSDB 单一马尔可夫链的未来路径预测概率为：

可以从矩阵结果中取概率值最大的前n个状态的集合或者取大于规定阈值的状态集合作为模型的预测结果。

3 多维融合马尔可夫路径预测模型

在采用单一马尔可夫链预测t时刻车辆的未来路径序列时，只采用了门架序列数据库这一路网维度特征对所有车辆的行驶路径进行预测。但是车辆的行驶行为是一个复杂的过程，会受到多种因素的影响，采用多维数据融合技术，将车辆类别、行驶时间等维度的数据融合至预测模型，从细致的维度来描述车辆的通行特征，预测结果将会更加精准[3-4]。

3.1 ETC 门架多维数据融合过程

ETC 门架数据融合经历了数据获取、数据预处理、特征提取、维度分类、融合决策的过程。如图1 所示，从ETC 门架系统中获取ETC 门架数据后，根据应用方向选取样本数据，从样本数据中提取应用特征，如车辆特征、门架特征、时间特征、路网特征等，将特征进行维度分类，将分类后的各个维度及下钻维度输入融合决策模型，最终得到决策结果。

图1 数据融合过程

（1）门架数据及相关样本数据。ETC 门架系统产生的数据包括：ETC 门架交易流水、ETC 通行记录、牌识流水记录、CPC 卡通行记录、原始收费数据、异常交易数据、抓拍图片、视频、日志数据和主要设备设施状态数据等。需要采用这些原始数据的数据库表生成新的用于构建GSDB 和实现路径预测的表，并采集样本数据进行概率计算。部分核心信息如表1 所列。

表1 ETC 门架部分核心信息

（2）门架数据维度处理。“维”让观察者能够从某个特定的角度观察到事物比较显而易见的属性，不同的角度所观察到的属性是割裂的，但是利用“维”之间的交汇点实现多个“维”的融合后，能够从全局的角度生成新的事物属性。

将用于行驶路径预测的门架样本数据特征值分成时间维、路网维、车辆维。通过时间维能够观测到车辆行驶入口、出口、各个门架以及门架区间的具体时间和通行耗时；通过路网维能够观测到高速公路的门架分布、路网分布，生成门架序列数据库GSDB；通过车辆维能够观测到车辆车牌、车型、类别、颜色、速度等车辆的动态和静态特征。在进行维度融合并采用预测模型实现决策处理后，就能够推算出新的行驶特征结论，如图2所示。

图2 ETC 门架三维数据立方图

3.2 多维融合马尔可夫路径预测模型

如果仅采用该文2.3 节描述的基于ETC 门架序列的单一马尔可夫链进行决策处理，得到的行驶特征结论只能是：从A 入口驶入高速公路，行经某门架序列的车辆，从B 出口驶出的概率为pj。这一结论过于粗糙，存在较大误差。因此，该文进一步提出了多维数据融合的马尔可夫路径预测模型，目的是将车辆特征、行驶时间等维度的数据融合至预测模型，从更加细致的维度来描述车辆的通行特征，得到更加精准的预测结果。[5]如：某种车型的车辆在某个时间段内通过A 入口进入高速公路，以平均时速80 km/h 行经某门架序列的概率为pj，满足以上条件的车辆，从B 出口驶出的概率为pj。

基于车辆通行行为特征实现车辆维度分类，通行行为包括入/出口组合、GSDB 中的门架序列组合、平均时速、通行车道等。车辆类别的统计归类采用聚类算法实现，使得同一类车辆之间的通行行为特征相似度最高。设C={c1,c2, …,ck}表示车辆的类别，任意车辆属于类别的概率为PC，则：

基于车辆通行时间实现车辆时间维度分类，通行时间包括行经入/出口时间、行经门架时间。设T={t1,t2, …,tm}表示时间类别，假设某辆车t时刻的时间类别为t1，表达的意思是某辆车在t时刻经过了某入口/出口/门架，或在t时间段经过了某门架序列，该车辆时间类别为ti的概率为Pti，则：

多维数据融合的马尔可夫链表示为：M=。其中，X是GSDB 的集合，可表示为{x1,x2, …,xn}，每个xi对应一个门架序列{x1,x2, …,xn}，称为模型的一个状态；K表示车辆维度的类别数，C={c1,c2,…,ck}表示车辆的类别，P(C)表示不同类别车辆的概率分布；T表示时间维度的类别数，P(T)表示不同时间类别的概率分布；MCT={mct11, mct12, …, mct1n}{mctk1, mctk2,…, mctkn}，表示融合时间维和车辆维的马尔可夫链集合，每一个元素mctkn描述了车辆类别为ck、时间类别为tn的马尔可夫链，它的转移概率矩阵表示为：

假设某辆车在t时刻生成的车辆路径序列为x，状态用xt表示，则t时刻处于状态xi的第i维等于1, 其余各维都为0。则多维数据融合的马尔可夫链的未来路径预测概率为：

可以从矩阵结果中取概率值最大的前n个状态的集合或者取大于规定阈值的状态集合作为模型的预测结果。

4 结束语

该文在对目前成熟的路径预测模型进行比较后，针对当前已经被门架覆盖全网的高速公路路网环境，采用马尔可夫链实现未来行驶路径预测。通过建立ETC 门架序列数据库（GSDB），实现了对路网维的数据表示，基于GSDB 的单一马尔可夫链的路径预测结果可以是经过下一个门架的概率、经过下一个出口的概率、经过下一个门架序列的概率等。但是单一马尔可夫链的预测准确率不高，因此我们提出了多维融合的马尔可夫路径预测模型，该模型引入了车辆维度和时间维度进行更加细致的特征分类，能够更加明确地对车辆行为特征进行描述和划分，预测结果更具有参考性。