基于序贯平差的沉降预测模型高效更新方法

郑一帆，于先文

(东南大学 交通学院，江苏 南京 211189)

不均匀沉降是导致建构筑物开裂、塌陷等结构性破坏的主要原因之一，严重影响建构筑物的服务性能，威胁其安全性与稳定性[1]。沉降预测是目前大多数工程进行地基处理的主要依据，其预测结果与工后不均匀沉降的处理效果密切相关。沉降预测分为两个步骤，首先使用工程的实测沉降数据建立沉降预测模型，然后通过沉降预测模型预测工后沉降。随着工程进展，沉降预测模型需要不断地更新来保障预测的质量。对于高铁、大型桥梁等时间跨度大的工程项目，建立一个沉降预测模型高效更新的方法具有重要的意义。

目前，沉降预测模型的更新普遍采用简单的传统更新方法。在实际的工程中，广泛使用的模型如双曲线法模型[2-4]、指数曲线法模型[4-6]、星野法模型[8-9]等都使用传统最小二乘方法进行模型更新。该方法的具体过程为：新增观测数据后，利用全部数据列出误差方程进行最小二乘间接平差，得到新的沉降预测模型系数。即便被广泛应用于实际工程中，传统更新方法也仍存在不足之处，具体表现为以下三点：①数据存储量大，需要将历史沉降数据全部保存，历史沉降观测数据重复地参与拟合过程；②模型更新计算量大，每次更新过程都需要使用到所有的沉降数据，计算过程中的矩阵维数可能会非常高；③存在数据损失风险，由于历史数据数量庞大，可能存在数据丢失、被篡改、误录入等现象，对预测模型的正确更新带来风险。

针对传统更新方法所存在的这些问题，本文将序贯平差理论[10-12]应用到沉降预测模型更新的领域，导出详细计算流程和相关系数算法，以避免历史数据的存储，有效提高模型更新效率，并通过工程算例验证新方法的正确性和高效性。

1 模型的传统更新方法

不同沉降预测模型的方程有一定的差别，但包括双曲线法模型，指数曲线法模型，星野法模型在内的绝大多数模型可以表达为统一的二维线性形式，其表达式为

y=a0+a1×f(t)

(1)

式中：a0、a1为模型系数；t为观测时间；y为包含t时刻沉降信息的因变量，为便于表达，下文直接用沉降观测量指代。

在获取第n+1期新观测的沉降量yn+1后，使用传统的更新方法对沉降预测模型进行更新。首先利用全部n+1期沉降数据列出n+1维的误差方程组

V=Aa(n+1)-Y

(2)

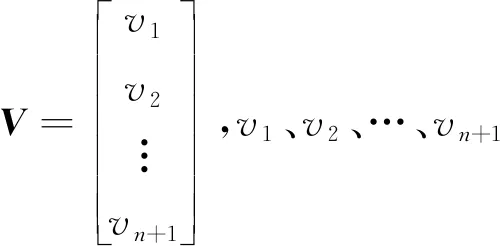
利用最小二乘法可得系数矩阵的估值

(3)

式中：P为观测值的权矩阵，其确定方法可参考文献[16]。

根据式(3)可得更新后的沉降预测模型为

(4)

计算预测模型的相关系数为

(5)

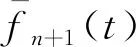
传统更新方法算法简单，但是随着观测时期的延长，沉降观测数据的不断增加，误差方程组的扩充降低了计算的效率。同时，历史观测数据转抄等过程中可能发生错漏，大量存储的历史观测数据增加了模型更新发生错误的风险。

2 基于序贯平差的模型高效更新方法

2.1 高效更新方法

序贯平差方法的核心思想是利用前期平差结果和当前观测数据进行逐次平差[10]，在测量的多个领域已有成功的应用[13-15]。为改善传统更新方法的缺陷，将序贯平差理论引入沉降预测模型更新过程中，以得到模型高效更新方法。

基于前m(m≥2)期数据，利用最小二乘法首次得到沉降预测模型为

(6)

以及首个系数向量估值的权阵为

W(m)=ATPA

(7)

自m+1期起，即可利用序贯理论进行模型更新。下面以第n+1(n≥m)期数据为例，导出沉降预测模型高效更新计算公式。

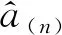
(8)

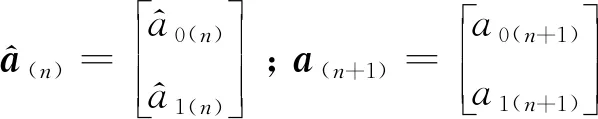
第n+1期新增沉降观测数据为yn+1，相应权为pn+1，可建立观测误差方程为

(9)

将式(8)与式(9)联立，得误差方程式为

(10)

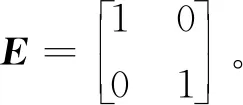
根据最小二乘法，可得当前预测模型系数的最优估值为

(11)

相应的权阵为

(12)

于是，高效更新后的沉降预测模型为

(13)

在上述方法中，历史观测数据对模型的影响已全部映射到预测模型的系数估值及其权阵中，利用序贯平差理论更新预测模型，已间接利用了历史观测数据。因此，该方法具有不需存储历史观测数据，计算量小，更新出错概率低等优点。

2.2 相关系数递推算法

沉降预测模型的评价过程中，相关系数是个比较重要的指标[17-18]，式( 5 )所示的传统相关系数计算过程需要使用全部历史数据，因此需推导与高效更新法相应的相关系数计算公式。

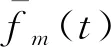
(14)

(15)

自m+1期起，即可利用递推公式更新模型的相关系数，同样以第n+1(n≥m)期数据为例，导出相关系数递推公式。

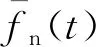
(16)

其中，离差平方和k1(n+1)可化为

(17)

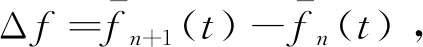
(18)

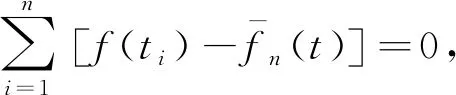
(19)

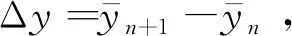
(20)

式(16)的分子可表示为

(21)

(22)

(23)

所以，综合式(16)、式(20)～式(23)的结果，可得相关系数γn+1的递推式为

(24)

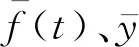
相关系数的递推计算公式与高效更新方法保持了高度的一致，充分利用了递推前的相关系数所包含的历史数据信息，省略大量存储、计算内容，降低了风险，提高了效率。

3 应用流程

以上内容介绍了模型高效更新方法的具体原理与详细过程，为了更方便地对该方法进行利用，现将其应用流程总结为如下三个主要步骤：

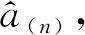
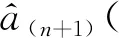
Step3计算更新后模型的相关系数γn+1(式(24))用以模型评价。

4 工程算例

4.1 工程背景

本文以桥梁沉降模型为例，对沉降预测模型的高效更新方法进行算例验证。实验数据选取沪苏通长江公铁大桥HTQ-1标段工程6#墩的实测沉降数据，从第4期开始构建沉降预测模型；实验模型方法选用沉降预测模型中最常见的双曲线模型，其模型表达式为

(25)

式中：S0、t0分别为架梁完工时的沉降量、观测时间；α、β为根据实测值求出的系数；St、t分别为任意时间的沉降量、所对应的时间。

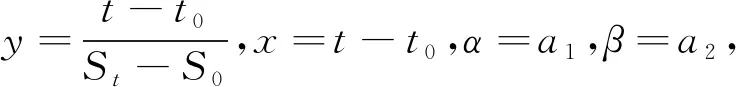
y=a0+a1x

(26)

根据模型的线性方程可以进行更新，更新完成后也可以得到模型的原表达式结果。

4.2 方法性能比较

选取全部观测数据，用传统更新方法随时间更新沉降预测模型，更新结果见表1。

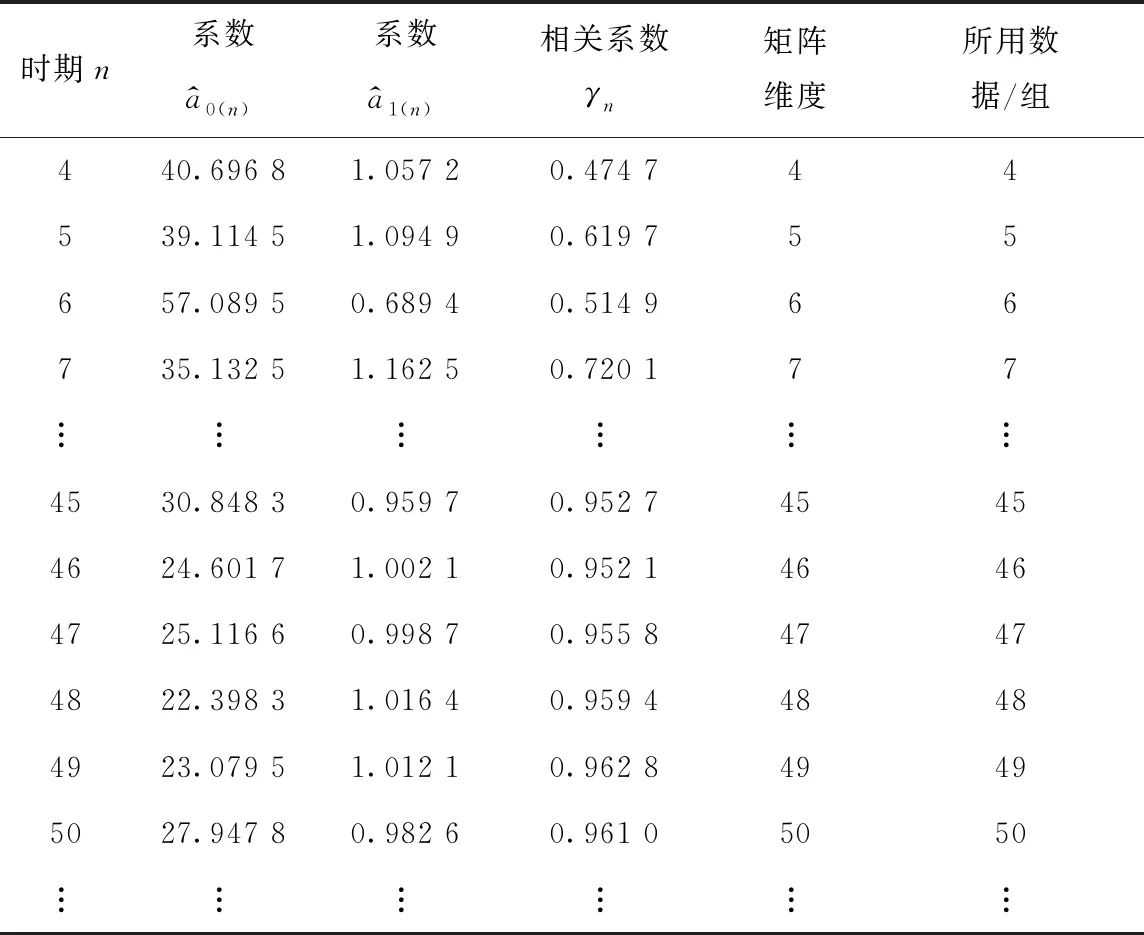
表1 传统更新方法的更新结果

由表1可见，模型包含的数据量越多，其相关系数越趋近于1，表明其拟合效果越好。但与此同时，模型更新所需要的数据量与矩阵维度也快速增加，工程的计算量和计算复杂程度都会增加。

同样的数据，按高效更新方法进行沉降预测模型的更新，更新结果见表2。

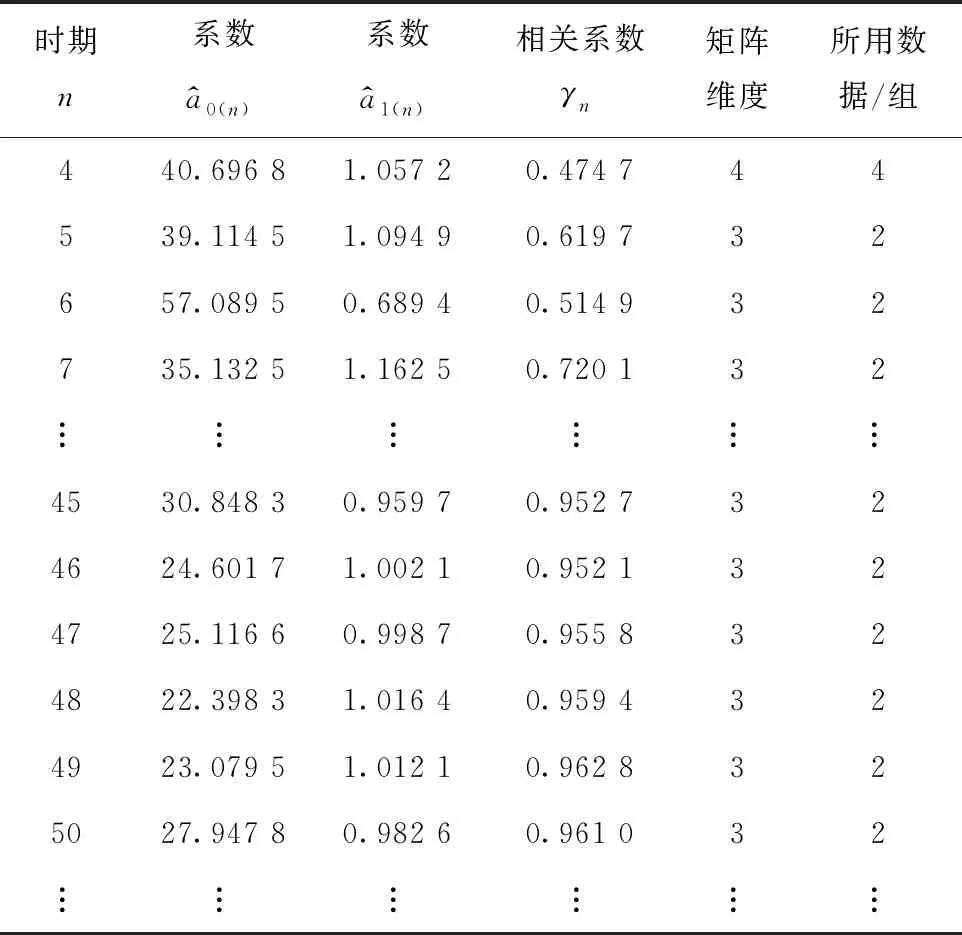
表2 高效更新方法的更新结果

由表2可见，高效更新方法与传统更新方法得到的结果都完全一致，但在矩阵维度和所用数据方面，高效更新方法维度更小，使用数据更少。这表明在实际应用中，伴随着工程进展，高效更新方法节约存储、减少运算的优势也会愈发凸显。

5 结论

本文为解决传统更新方法存储量大、模型更新计算量大、存在数据误用风险等问题，引入序贯平差的理论，对沉降预测模型的更新方法进行优化，得到了模型的高效更新方法，导出了相应的相关系数递推公式，并利用实测数据对新方法进行了对比验证。理论和算例均表明，本文新方法具有以下优点：

(1)避免了存储历史观测值的麻烦。当前预测模型系数的先验信息已包含了历史观测数据对模型影响的全部信息，因此不需存储历史观测数据。

(2)提高了算法效率。高效更新方法只利用到了预测模型系数的相关信息，以及当前最新沉降观测值信息，极大降低了计算过程中的矩阵维度，可显著提高计算速度。

(3)提高了模型更新的可靠性。数据在存储、拷贝、录入过程中可能会存在丢失、被篡改、误录入的风险，新方法无需大量存储、频繁使用历史数据，可杜绝此类风险，保证模型的正确更新。