边底水碳酸盐岩气藏提高采收率的微观驱气效率

吴克柳 朱清源 陈掌星,2 李 靖 冯 东 王牧原 郭世强 郭豫川

1.“油气资源与探测”国家重点实验室•中国石油大学（北京） 2.加拿大卡尔加里大学化学与石油工程系

0 引言

边底水碳酸盐岩气藏储量丰富，广泛分布在塔里木盆地、四川盆地、鄂尔多斯盆地[1]。该类气藏在开发中后期会出现边底水侵，引起驱气效率和采收率的下降[2]。水侵后，复杂的气水接触关系会引起额外的流动阻力。对于非均质性较强的碳酸盐岩储层，水窜或绕流会造成大量圈闭气，降低波及效率[3-4]。此类气藏开发，不仅要研究宏观矿场尺度的生产动态特征，还要揭示微观孔隙尺度的水气两相渗流机制，才能更好地明确微观驱气效率的主控因素，指导气井生产制度优化，从而提高气藏开发效果。

近年来，随着微观孔隙结构研究手段的进步，许多学者通过岩石铸体薄片或CT扫描直接观测碳酸盐岩的微观孔隙结构，结合激光刻蚀技术[5-9]或微电子光刻等手段[10]，建立能够反映地下真实多孔介质的玻璃刻蚀模型。基于此模型开展气水两相流动物理模拟，观测气驱水、水驱气过程中水气分布及两相渗流特征。可视化实验表明，水驱气形成封闭气的方式有指进、卡断、孔隙盲端和角隅、H孔道、绕流等[8]。借助图像处理技术，还可定量分析气水分布模式[11]。

相较于物理模拟，研究人员还可直接在多孔介质孔隙空间内开展计算流体动力学（Computational Fluid Dynamics，CFD）的数值模拟，更加灵活精细地揭示孔隙尺度单相或多相流体渗流规律[12]。许多学者通过不同数值模拟方法，如水平集法[13]、相场法[14]、格子玻尔兹曼[15-16]、孔隙网络模拟[17]等，研究了水驱油[14]、气驱油[15,18]、渗吸[19]等过程中的多相渗流特征。然而，关于水驱气的直接数值模拟研究较少，虽然有学者通过水平集法研究了煤层[13]、土壤[20]、花岗岩[21]等多孔结构中的水气渗流，但Akhlaghi等[22]研究表明相场法更适合于多孔介质两相流动问题。为此，本文将从孔隙尺度数值模拟的角度，采用相场方法研究边底水碳酸盐岩气藏水驱气渗流特征，探究明确微观驱气效率的主控因素，尝试为提高采收率方案设计提供理论指导。

1 孔隙尺度水气流动模拟

为构建孔隙尺度水气非混相流动模拟方法，提出以下假设条件：①水气两相均不可压缩；②忽略重力影响；③忽略气在水中的溶解；④多孔介质内气水流动符合等温层流。

1.1 流体运动方程

流体运动方程为质量和动量守恒方程，即连续性方程和N-S方程为[23]：

式中u表示流速，m/s；ρ表示密度，kg/m3；t表示时间，s；p表示流体压力，Pa；I表示单位向量；μ表示动力黏度，Pa·s；Fst表示两相界面张力项，由下文相变量获得，N/m3。

1.2 界面追踪方程

多相流动的CFD方法通过N-S方程描述多相流体流动机制，同时耦合关于相变量的对流扩散方程实现界面追踪，如：水平集法、相场法、流体体积法等。Akhlaghi等研究表明，相场法更适合于模拟多孔介质中非混相两相流动[22]。本研究中采用相场法，该方法将多相界面描述为具有一定厚度的扩散界面层，在此区域相变量ϕ逐渐由－1（某一相）过渡到1（另一相），因此其本质上仍为连续方法而无须区分相与界面[24-25]。相变量的演化方程为由自由能引出的Cahn-Hilliard方程，描述了对流和扩散作用影响下的相分离过程[26]。

式中ϕ表示无因次相变量；γ表示迁移率，表示扩散作用对界面的影响，m2·s/kg；λ表示混合自由能密度，N；ε表示界面厚度，与λ共同决定界面张力，m；ψ表示相场助变量，将原来的四阶对流扩散方程变为式（3）中两个待求解的二阶偏微分方程，从而降低求解难度[24]。

界面张力为单位表面积的额外自由能，表示为[24,27]：

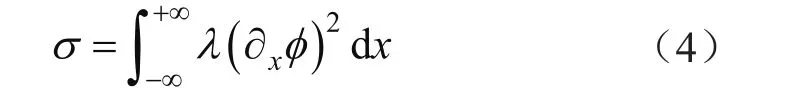
自由能函数对相变量的变分可获得化学势G为[24]：

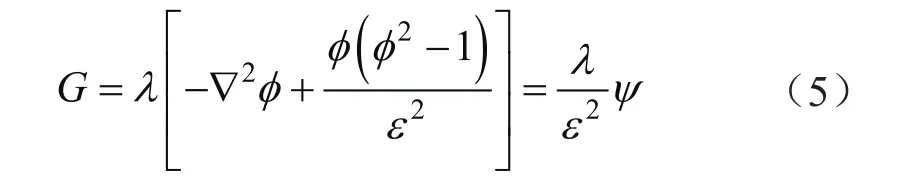
进而可求出界面张力作用项为[24]：

计算域内流体的密度和黏度为两相对应物理量的体积平均为[25]：

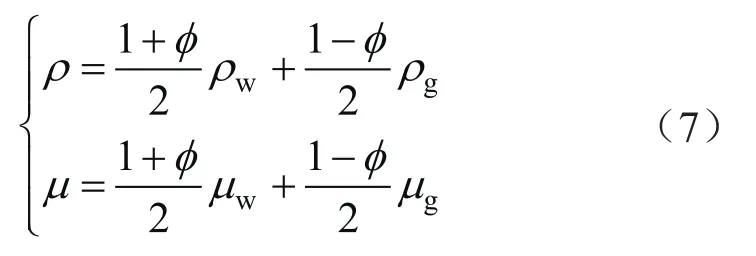
式中下标w和g分别表示水相和气相。

运动方程的固体边界条件为无滑移边界，且相变量不穿越固体边界为：

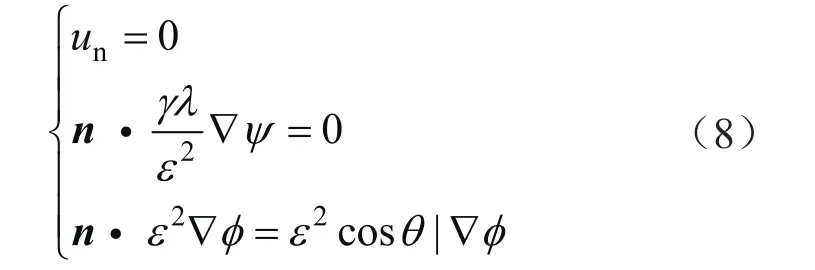
式中un表示固体壁面的流体速度，m/s；n表示固体壁面的单位法向量；θ为接触角，（°）。

1.3 动态接触角

由式（8）可以看出，润湿角决定了相变量在边界的演化。为了更准确描述水气前缘的形态和推进过程，本文采用动态润湿角，即润湿角随三相接触线速度而变化。基于水动力学理论，Cox详细推导出了动态润湿角模型[28]，即θd3～Ca。本文采用基于Cox水动力学模型的简化形式[29]为：

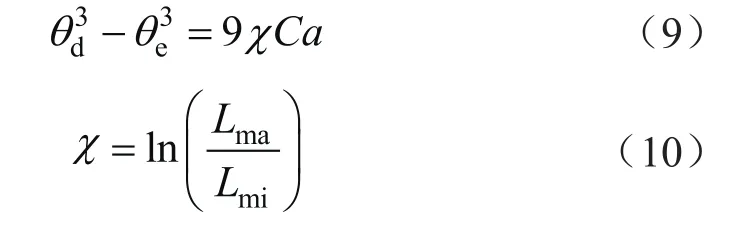
式中θd、θe分别表示动态润湿角、平衡接触角，（°）；Ca表示毛细管（以下简称毛管）数，表征黏滞力和毛管力的相对强度，Ca = μv/σ，无量纲；Lma表示宏观尺度，对应孔喉尺寸，m；Lmi表示微观尺度，对应分子尺寸，m。在多数研究中，通常取χ=16[30]。需要指出，毛管数中的速度为三相接触线速度。考虑到难以直接捕捉每一个三相接触点的速度，在以下研究中使用入口速度近似。

2 模型验证

2.1 分层两相流

为了验证相场模型是否适合描述非混相流动，进行了经典分层两相流测试[15]。如图1所示，两平板高度2b，中心位于y=0，其中a>|y|>0为非湿相区域，|y|>a为湿相区域。在x方向对两区域分别施加Gw和Gnw的体积力。两种流体密度相同，黏度不同，并服从泊肃叶流动，则速度剖面的理论解析解为：

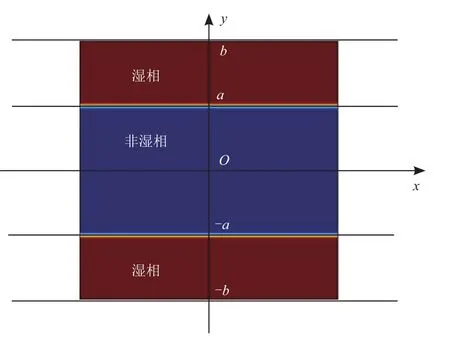
图1 分层两相流示意图

式中 A1=-Gnw/2μnw，A2=-Gw/2μw，B2=2(A1M-A2)a，C1=(A2-A1)a2-B2(b-a)-A2b2，C2=A2b2-B2b；M 表 示 非湿相与湿相运动黏度比。

构建200×100 μm的二维平板，湿相与非湿相黏度分别为1 mPa·s和0.01 mPa·s，分别施加体积力，计算结果如图2所示。可以看出数值解与解析解一致。

图2 分层两相流速度剖面数值解与解析解对比图

2.2 单管渗吸

为了验证相场方法是否适用于描述流固作用力引起的接触角问题，将模型数值解与Lucas−Washburn方程解析解进行对比[15]。如图3所示，建立毛细填充的渗吸数值模型。模型与湿相流体相邻，初始时刻充满非湿相流体，在毛细管动力和黏滞阻力共同作用下，湿相流体自发渗吸驱替非湿相流体。忽略重力和惯性力时，获得渗吸距离的理论解为：

图3 毛细填充模型示意图

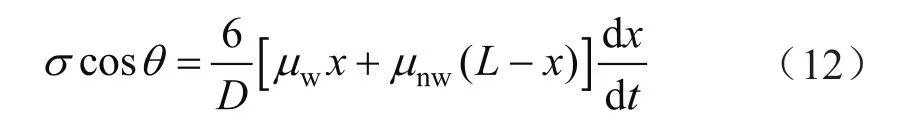
式中D表示毛细管直径，m；x表示渗吸距离，m；L表示毛细管长度，m；t表示渗吸时间，s。

数值模型中，D=30 μm，L=1 000 μm，μw=0.01 Pa·s，μnw=0.001 Pa·s，界面张力0.08 N/m，平衡接触角θ=30°，两相密度均为1 000 kg/m3。如图4所示，渗吸前期，惯性力影响大，考虑惯性影响的数值解低于理论解；而渗吸后期，惯性力影响减弱，数值解较好地符合解析解。

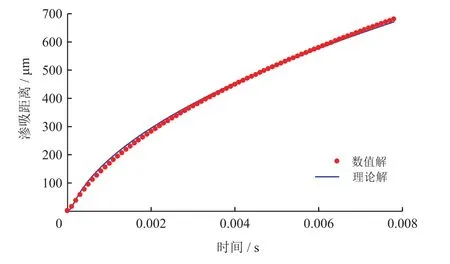
图4 渗吸距离数值解与解析解对比图

3 结果与讨论

采用随机生长四参数生成法（quartet structure generation set，QSGS），通过控制各个方向的固相生长概率，构建300 μm×300 μm的非均质多孔介质[31]，用以代表碳酸盐岩储层水气渗流空间（图5-a）。

图5 多孔介质生成过程图

然后通过腐蚀膨胀平滑基质岩石颗粒的轮廓[32]，分割相邻岩石颗粒狭窄胶结区域的连接，同时去掉颗粒周围细小的突出部分（图5-b）。为了凸显非均质性，手动添加若干岩石颗粒，最后进行网格剖分及有限元求解，网格平均质量为0.847 8（图5-c）。使用前文所述相场模型模拟水驱气过程。在基础算例中，水和甲烷气的密度 ρw和 ρg分别为 1 000 kg/m3和 100 kg/m3；黏度μw和μg分别为1 mPa·s和0.01 mPa·s；界面张力50 mN/m；式（3）中界面厚度为最大网格尺寸的1/4。

模型初始饱和气，假设左侧连接水体，水相从左端恒流量（0.2 m/s）流入；水气从右端流出，静压0 Pa；岩石表面亲水，平衡润湿角60°；流体在岩石表面无滑移。由于界面厚度与网格尺寸有关，因此需进行网格独立性检验。如图6所示，可以看出，不同网格数下模拟结果基本一致。为了保证计算效率和精度，本研究中选取网格数为93 400。

图6 网格独立性检验图

3.1 剩余气分布及形成机理

图7为基础算例不同驱替时刻的剩余气分布，白色为岩石颗粒，红色为水相，蓝色为气相。刚开始注入水相时，界面推进相对均匀。当界面接触到小孔喉区域（图7-a红色框）时，会突然加速，该现象对应于实验中观测到的毛管指进[8]。这是由于小孔喉区域内，驱替压差和较强的毛细管动力对流动的促进作用克服了黏滞阻力的抑制作用。当界面移动出小孔喉区域时，水气界面形态在喉道出口处发生反转，毛管力由动力变为阻力，造成额外毛管阻力（图7-c红蓝框），即毛细阀效应[33-34]。且孔径越小，阻力效应越严重（图7-c红框）。这种滞后现象，缓解了毛管指进引起的水相快速突破，一定程度地促进了水线的均匀发展。在图7-d、e中，观察到大孔喉中（红框）界面速度高于小孔喉（蓝框）中，这是由于蓝色框内迂曲度更大，造成了更多的能量损失。最终，观察到3类剩余气（图7-f）：盲端剩余气（红色框内）、孔喉间剩余气（绿色框内）和簇状剩余气（蓝色框内）。需要指出，本研究中未考虑湿相驱替非湿相时，湿相在壁面上的膜状流[35]，因此没有观察到喉道壁面水膜聚并对气相造成的卡断[8]。

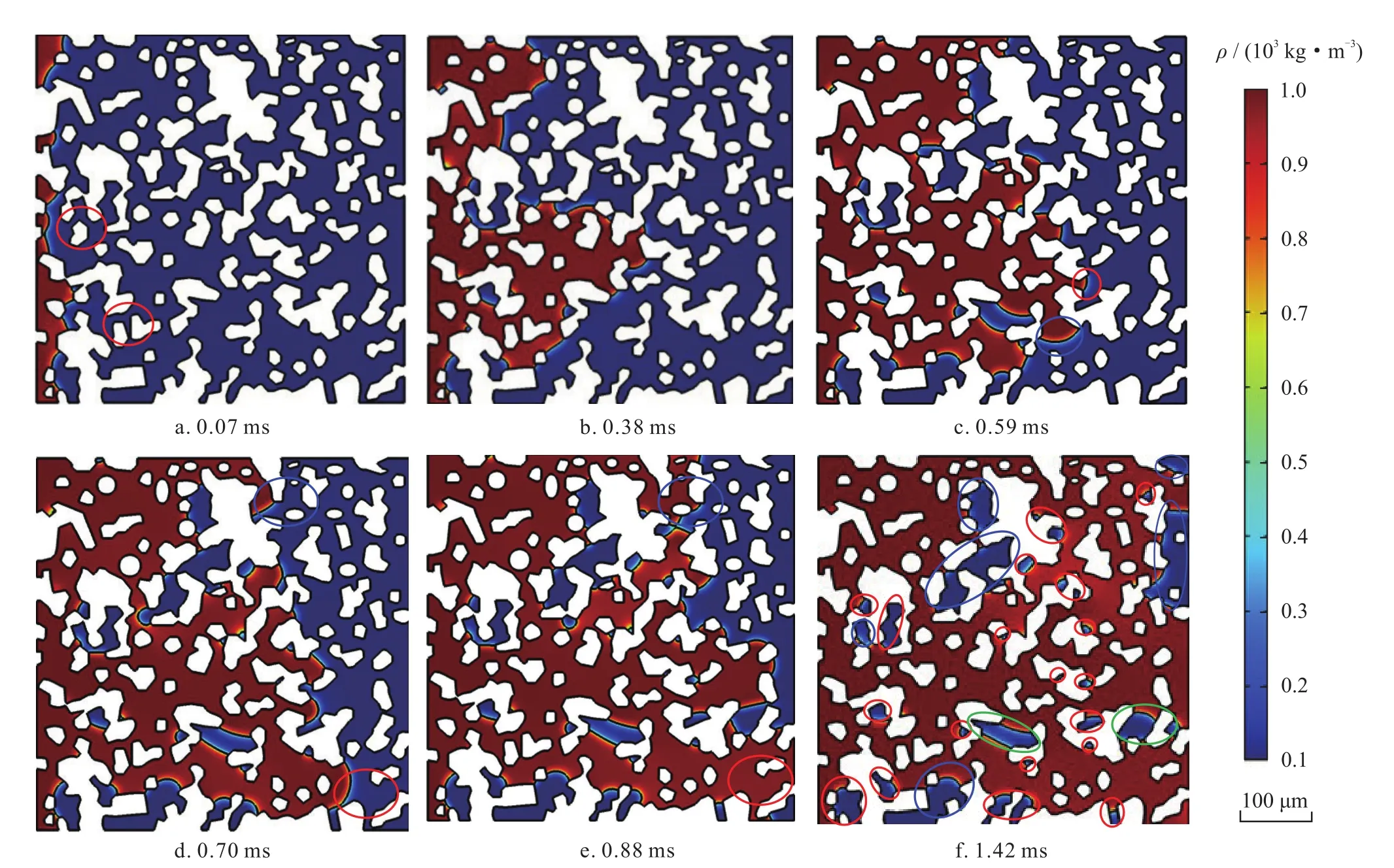
图7 基础算例不同时刻剩余气分布图

3.1.1 盲端剩余气

盲端剩余气分布较分散，其形成主要取决于微观孔隙结构。如图8-a所示，当界面前缘遇到盲端孔隙后，受壁面吸附力作用，水会流向盲端孔隙，此时界面发生变形，曲率半径变大[35]。当界面与孔隙边界顶点相切时（0.4 ms），界面被截断，在盲端孔隙中形成新的界面并在毛管力的作用下迅速变形，束缚住盲端内部气体。第二种形成机制是多个界面在盲端孔隙外聚并，分割了盲端孔隙内外气相（图8-e）。滞留气量取决于孔喉比、润湿性、驱替速度。如图8所示，驱替速度越大（图8-a、b对比）、盲端孔隙越深（图8-a、c对比）、孔喉比越大（图8-a、d对比），盲端孔隙气体滞留比例越大。若要减少盲端剩余气的形成，需降低采气速度；若要动用已形成的盲端剩余气，即使提高驱替速度也难以启动，只有生产端降压引起气体膨胀，改变压力状态，方可动用。

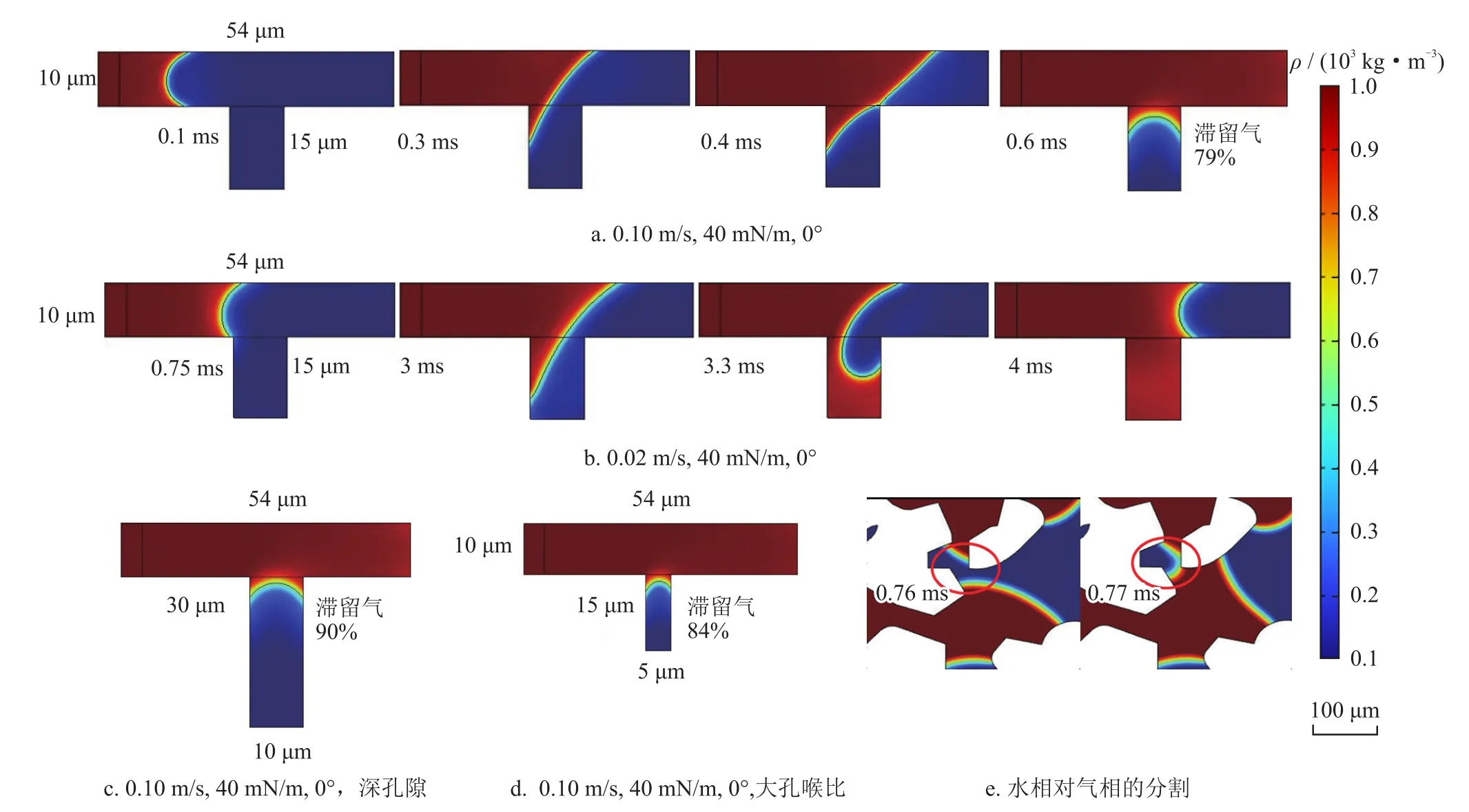
图8 盲端剩余气形成过程图

3.1.2 孔喉间剩余气

孔喉间剩余气的形成机理有两种。第一种来源于喉道连接的两个孔隙内水相同时流入。如图9-a所示，界面前缘推进至某一孔隙时，水会流向喉道。当相邻孔隙也被水充填时，水相也会向喉道内运移，从而将相邻孔隙间喉道中的气堵死。该机制同样适合描述孔洞缝碳酸盐岩气藏中，连接两个孔洞的裂缝中滞留气柱的形成过程[10]。第二种来源于水相对气相的分割。如图9-b所示，0.86 ms时，红色框内的水气界面在驱替压力和毛管力作用下克服黏滞力向前流动；0.89 ms时，界面与固体颗粒接触（黑色框内），形成孔喉间剩余气柱（绿色框内）。若要减少孔喉间剩余气的形成，需降低采气速度；若要动用已形成的孔喉间剩余气，需放大生产压差，依靠气泡、气柱膨胀或打破原有压力系统，最终克服毛管阻力从而流出。

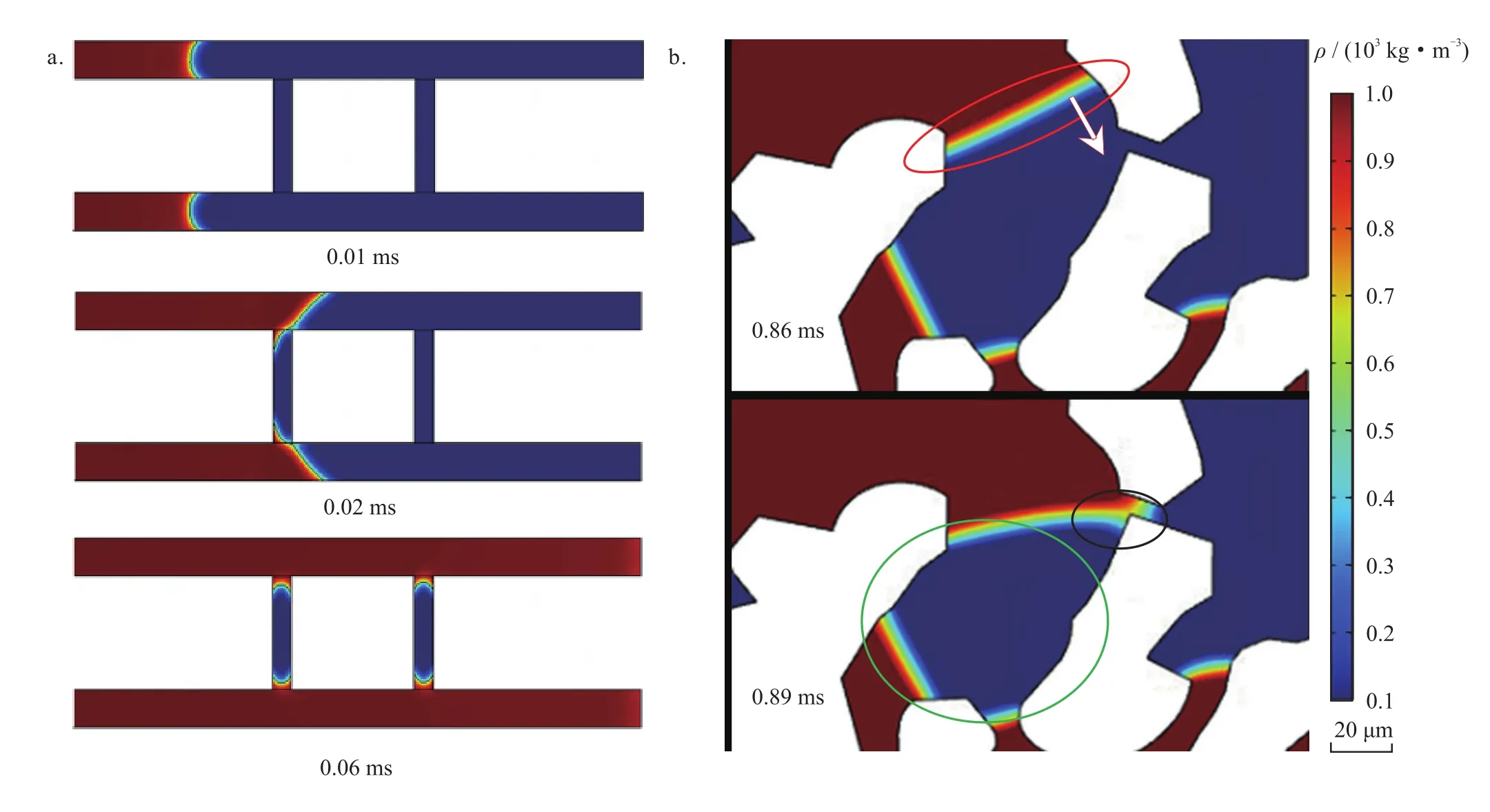
图9 孔喉间剩余气形成过程图

3.1.3 簇状剩余气

簇状剩余气主要是孔喉结构非均质性造成的界面推进不均匀而形成的。当发生毛管指进时，水相在小孔喉区域的快速流动，会绕过大孔喉区域，以至于后期无法克服簇状剩余气柱产生的毛管阻力；当发生水动力指进时，小孔喉中气体被滞留；当多股水相优势通道的界面相遇时，也会将内部区域的气封闭，并形成滞留气。因此，滞留气规模主要取决于储层非均质程度及其与驱替速度的协同性。对于非均质性较强的碳酸盐岩气藏，该问题更加突出。若要减少簇状剩余气的形成，需考虑储层非均质性与采气速度的协同性；若要动用已形成的簇状剩余气，需放大两端压差，从而使簇状剩余气柱克服毛管阻力流向生产端。

3.2 微观驱气效率变化机制

图10为微观驱气效率和出口含水率随驱替时间的变化曲线。可以看出，水相开始侵入至0.80 ms前，气体采出程度呈线性增加，出口端仅产气，这是由于水气前缘还未推进至出口端。当0.80 ms时，出口端见水，含水率台阶式上升，微观驱气效率增速变缓，该阶段为第一条水相优势通道的形成（图11-a）。当1.06 ms时，形成第二条水相优势通道（图11-b），含水率再次急剧上升，微观驱气效率进一步变缓。随后，每一次水相优势通道的突破或扩大都会引起驱气效率的增速减缓（图11-c、d）。由此可见，见水后流场难以波及滞留气区域，造成水锁，形成残余气。

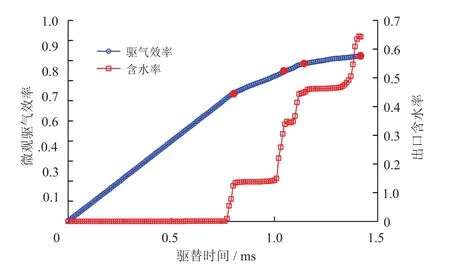
图10 微观驱气效率变化图

图11 水驱气流场分布图

3.3 微观驱气效率影响因素

3.3.1 驱替速度

图12展示了平衡接触角60°和气水界面张力70 mN/s时，注入速度分别为0.05 m/s和0.5 m/s（毛管数分别为 7.143×10－4和7.143×10－3）的水气分布及微观驱气效率变化。可以看出，在本文使用的多孔介质模型中，驱替速度越小，盲端剩余气比例越少（与3.1中结论一致），孔喉间剩余气也会减少。当低速驱替时，由于驱替压差较小，毛管力占主导，观察到了气水界面流出喉道时更加严重的毛细阀效应，以及更加频繁的海恩斯跳跃现象。

图12 不同驱替速度的剩余气分布及微观驱气效率对比图

3.3.2 界面张力

图13展示了平衡接触角60°和注入速度0.20 m/s时，界面张力分别为10 mN/m和70 mN/m（毛管数分别为2×10－2和2.857×10－3）的水气分布及微观驱气效率变化。可以看出，高界面张力下，孔喉间剩余气含量有所减少，部分区域界面推进速度慢。这是因为，虽然高界面张力能够为小孔喉带来较大的毛管动力，但当界面形态在喉道出口发生反转时毛管阻力也越大（图7-c）。整体而言，高界面张力下的微观驱气效率略高于低界面张力。

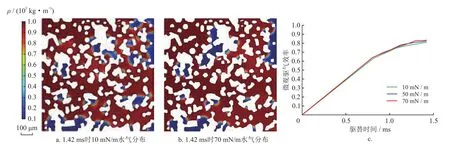
图13 不同界面张力的剩余气分布及微观驱气效率对比图

3.3.3 润湿性

图14为注入速度0.20 m/s和界面张力50 mN/m时，接触角分别为10°和90°的剩余气分布和驱气效率对比。毛管力在水湿介质中为动力，在中性润湿中由于动态接触角呈现阻力，故水湿介质的最终驱气效率更大，且中性润湿介质的微观驱气效率对水相突破更加敏感。从剩余气分布来看，中性润湿介质中出现了更多被水相分割的小气柱。

图14 不同润湿性的剩余气分布及微观驱气效率对比图

总的来说，微观驱气效率取决于水气界面是否均匀推进，而界面的移动受多种力的影响[36]：

式中 pin,e、pdis、pce,e、pv,w,e、pv,nv,e、pg,e、pen,e、pfl,e分别表示惯性力、驱替压力、毛管动力、湿相黏滞力、非湿相黏滞力、重力、入口端效应、和三相接触线摩擦力，Pa。

对于多孔介质中水气流动，由于低雷诺数（Re=ρvL/μ）和低邦德数（B=ρgr2/σ），可忽略惯性力和重力的影响；当不考虑入口端效应和动态接触角时，可忽略后两项。对于水驱气的强驱替动力条件下，驱替动力的作用强于毛管动力，而且小孔道中的黏滞力更强，故大孔道中前缘推进速度大于小孔道，从而将小孔道中的气封闭[8]。相反，对于水驱气的弱驱替动力条件下，毛管动力作用更显著，毛管指进明显，常体现出小孔中推进快，大孔中推进慢[5]；然而这种现象并不是绝对的，这是由于小孔道中的黏滞阻力也很强，甚至大于其毛管动力，这也是为什么某些实验中并未观测到小毛管指进现象[37]。因此，若要制订使水线尽可能均匀推进的气井生产压差，需揭示特定气藏储层微观孔隙结构和润湿性特征下的水驱气力学演变规律，才能提高气藏的开发效果。

4 结论

本文通过耦合Cahn-Hilliard界面追踪模型和N-S流体流动方程，使用随机四参数生长法生成非均质多孔介质，并模拟了多孔介质中水驱气非混相渗流，获得以下主要认识：

1）剩余气分布有盲端剩余气、孔喉间剩余气和簇状剩余气，其类型和规模受微观孔隙结构和毛管数影响。通过改变生产压差，打乱原有压力系统及气体膨胀，可进一步提高微观驱气效率。

2）微观驱气效率的变化与渗流过程息息相关，每一条水相优势通道的形成或扩大都会引起出口含水率的急剧上升并使驱气效率的增速变缓。

3）微观孔隙结构、润湿性和毛管数都影响水气界面的演化和微观驱气效率。在实际气井生产中，需基于储层微观孔隙结构和润湿性特征，明确水驱气过程中界面推进力学机制的演变规律，优化毛管数，从而确定最大化采收率的气井生产压差。