基于局域均值分解的行星齿轮箱故障诊断方法*
邓敦杰,李 鹏,王艺光
(桂林电子科技大学 海洋工程学院,广西 北海 536000)
0 引 言
在机械设备的生产过程中,不同机械设备形成一个整体,一旦有一处位置发生故障,将影响到整个机器的运行,导致其无法正常工作。因此,对机械设备进行设备运行状态监测及故障诊断具有十分重要的意义[1-2]。
目前,低速旋转机械在能源、采矿、冶金机械等领域得到了广泛应用。低速旋转机械的承载力大、工作条件差,其健康状况对于维持设备的正常运行和防止灾难事故的发生起着至关重要的作用。
其中,行星齿轮箱是旋转机械设备的重要组成部分。行星齿轮箱是连接以及传递动力的常用机械设备,是故障概率比较高的设备部件之一,在运输机械及石油、电力等领域也得到了广泛应用。当行星齿轮箱出现故障时,将对企业整个生产链产生影响,同时带来巨大的经济损失。因此,对行星齿轮箱进行状态监控与故障诊断,确保行星齿轮箱的安全、稳定运转具有重要意义。
近年来,国内外诸多相关专家针对行星齿轮箱故障诊断方面展开了大量研究。
陈仁祥等人[3]根据信号分布特征,构建了深度信念网络(deep belief network,DBN)模型,通过调整微调DBN模型的网络权重以及偏置值,完成了对目标的识别,并最终达到了故障诊断目标。朱静等人[4]优先采用了经验模态分解方式(empirical mode decomposition, EMD)对信号进行了去噪处理,将所得相关系数作为选取故障信号分量的依据,同时分析处理了选择的分量,通过提取故障信号特征,完成了对齿轮箱的故障诊断处理。贺妍等人[5]主要通过核主元分析,提取了不同类型的敏感性特征参数,构建了故障诊断系统,将全部数据输入到系统中,完成了对齿轮箱的故障诊断处理;该研究结果表明,所提方法可准确地诊断行星齿轮箱故障。VALLACHIRA S等人[6]基于数据驱动分类管理,提出了一种工业机器人所用的齿轮箱故障检测方法,评估了训练数据增强与估计测量、数据差异以抑制任务依赖性,从工业机器人收集的数据中选择了主成分数据,对齿轮箱故障进行了特征分类,实现了对齿轮箱的故障检测。GCA C等人[7]基于重加权广义极小凹稀疏正则化,提出了一种旋转机械振动故障诊断方法,利用了广义极小惩罚函数来规范加权稀疏表示模型,根据统计特征提出了一种重新加权策略,用于处理模拟信号和热铣传动齿轮箱的振动信号,实现了对齿轮箱的初期故障诊断。
上述文献中,针对行星齿轮箱故障诊断均采取了一定的措施,并得到了相应的诊断结果。但行星齿轮箱故障的微弱信号和强信号仍比较难以分离,导致行星齿轮箱微弱故障诊断容易受到强信号的干扰,诊断效果较差。
基于此,笔者提出一种基于局域均值分解的行星齿轮箱故障诊断方法,并进行相关研究。
首先,利用局部平均分解法对行星齿轮箱各振动信号进行分解,采用能量运算和周期频率进行解调,得到各分量的幅度和相位调制信息,从而精确地提取出行星变速箱微弱故障信号的特征;最后,将提取到的特征输入到最小二乘支持向量机(LSSVM)中,输出行星齿轮箱故障诊断结果,最终实现对齿轮箱的故障诊断。
1 行星齿轮箱故障诊断
1.1 行星齿轮箱振动信号降噪
笔者通过DASP数据采集系统(data acquisition & signal processing, DASP)对行星齿轮箱内各种振动信号进行采集处理。
在信号的采集过程中,由于受到不同因素的干扰,易造成信号中存在大量的噪声,进而导致信号整体平稳性较差,降低了齿轮箱故障诊断结果的准确性。因此,需要采用平移不变量小波降噪方法,对采集到的振动信号进行降噪处理[8]。
在已有去噪方法的基础上,业内已经提出了多分辨分析的有关概念及理论,可据此获取正交小波变换的计算方式。
根据上述理论,设定信号x(t)的采样离散数据为xk,则可获得与之对应的正交小波变换方法。
此处,笔者引入多分辨分析理论,可以得到行星齿轮箱振动信号x(t)的正交小波变换分解公式,即为:
(1)
式中:dj,k—尺度系数;ej,k—小波系数;gn-2k,hn-2k—滤波处理次数;k—常数;n—采样总次数。
从信号滤波角度来看,正交小波分解过程就是将离散信号分别采用高通及低通滤波器对采集到的信号实行滤波处理,得到信号的高频细节信息及低频概貌。
信号重构过程dj-1,k可表示为:
dj-1,k=∑(dj,k×hn-2k)+∑(dj-1×gn-2k)
(2)
要从被噪声污染的信号中恢复原始信号,对应的去噪步骤如下:
(1)计算含有噪声的信号,同时对其实行正交小波变换处理,选取最佳小波基和对应的分解层次,将包含噪声的信号实行小波分解处理,最终获取小波分解系数;
(2)阈值处理步骤(1)中的小波系数;
(3)对小波系数重构处理,获取对应的信号估计值。
虽然阈值方法获取的去噪效果比较显著,但在一些比较特殊的情况下,例如在信号的不连续领域内,阈值法自动将信号转换为非自然信号。
为有效解决上述问题,笔者通过平移不变量小波降噪来完成振动信号的去噪工作[9-11]。
基于平移不变量小波降噪的行星齿轮箱振动信号降噪流程,具体操作步骤如图1所示。
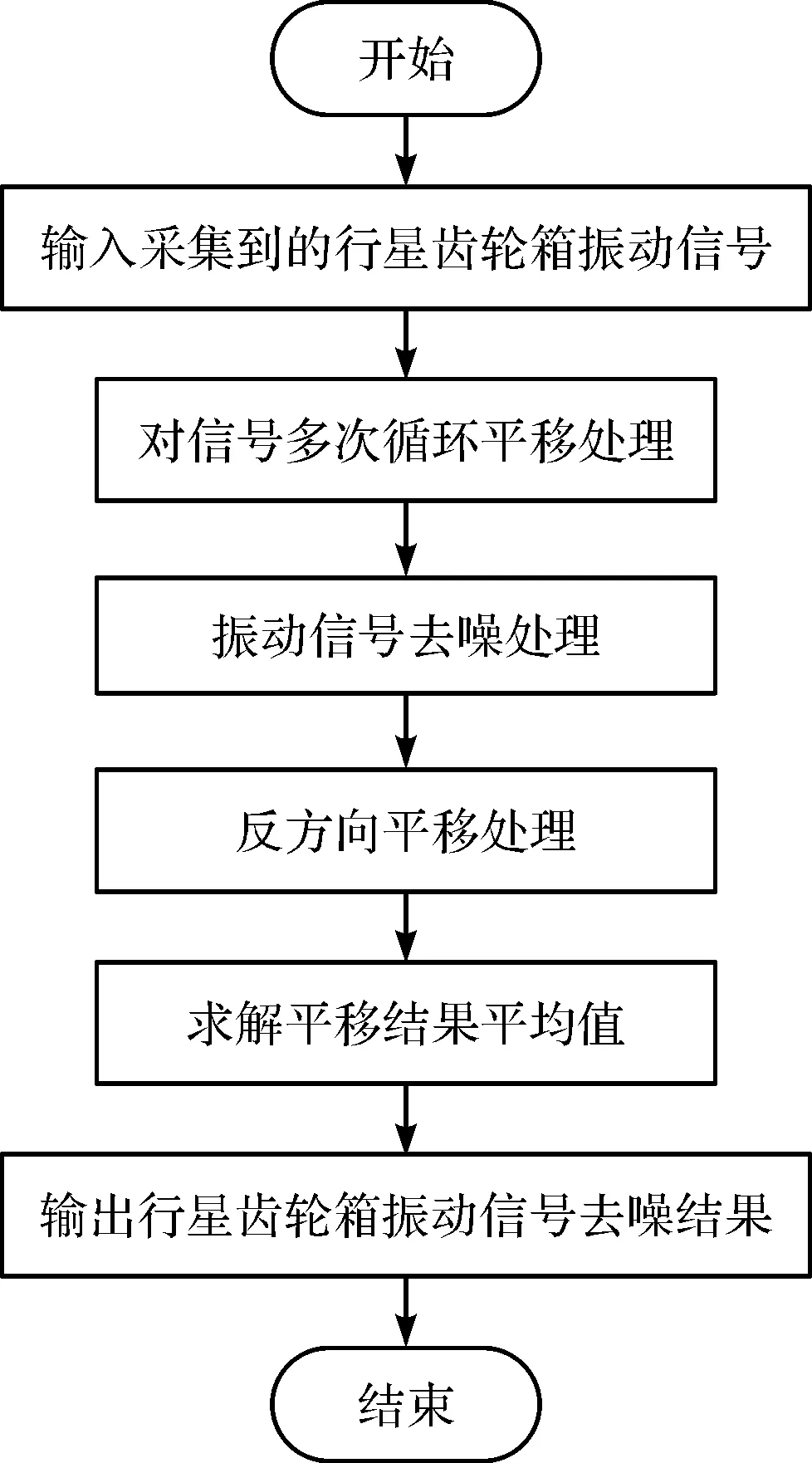
图1 行星齿轮箱振动信号降噪流程
笔者对图1流程进行细化,其步骤为:
(1)将采集的行星齿轮箱振动信号作为输入信号;
(2)对行星齿轮箱振动信号实行多次循环平移处理,则对应的计算公式为:
G(x,xk)=AvehellS-n*σ(ej,k)
(3)
式中:G(x,xk)—多次循环平移处理结果;Avehell—平移循环算子;S-n—方值差根;
(3)通过平移不变量降噪方法中的软阈值降噪方法对信号降噪处理,则对应的软阈值函数为:
(4)
式中:ωj,k—软阈值函数;λ—时间维度特征。
采用最高分辨率级的小波系数对噪声的标准差估计处理,从而得到下式:
(5)
式中:σ—标准差估计结果;
(4)再次对振动信号反方向平移处理,同时求解处理结果的平均值;
(5)输出行星齿轮箱振动信号降噪结果[12-14]。
1.2 基于局域均值分解的行星齿轮箱微弱信号提取
作为一种全新时频分析方法,目前,局域均值分解方法被广泛应用于多种信号处理工作中。
局域均值分解主要是为了将非平稳以及非线性信号分解,形成包络信号以及纯解调信号,根据二者乘积得到对应的行星齿轮箱微弱故障信号分量,同时得到时域及频域信号[15-17]。
针对行星齿轮箱的原始振动信号而言,其具体分析流程如下:
(1)确定行星齿轮箱原始振动信号x(t)的全部局域极值点hi,将其作为计算依据求得邻近极值点hi+1的平均值ki和包络平均值bi,公式如下:
(6)
(2)将步骤(1)所得数值进行平滑处理,获取局域均值函数n11(t)以及包络估计函数b11(t),将n11(t)单独进行分离处理后获取调频信号,其公式如下:
(7)
式中:m11(t)—调频信号;v11(t)—信号解调结果。
(3)判断包络估计函数是否满足设定的约束条件,如符合条件则说明m11(t)不是一个单纯调频信号,需要对其进行重复迭代处理,其计算公式为:
(8)
在实际的计算过程中,为了有效提升其计算效率,需要事先设定其变量,当满足约束条件时,则停止迭代过程;
(4)完成迭代操作后,计算得到的微弱故障信号F11(t)为:
(9)
式中:g11(t)—瞬时幅值函数。
笔者根据纯调频信号g11(t),对所得第一个微弱故障信号分量进行求解,以获取对应瞬时频率。
其计算公式为:
(10)
式中:r1(t)—瞬时频率;d—迭代次数;
(5)在行星齿轮箱中,准确分离第一个微弱故障信号分量,对剩余信号y1(t)分解处理,获取大量有利用价值的频率成分;将y1(t)设定为原始数据,重复上述操作步骤,分离获取第2个微弱故障信号分量,直至获取满足需求的单调函数,则停止计算。
准确分离的全部微弱故障信号分量为:
(11)
式中:yk(t)—第k个剩余微弱故障信号的分量;PFk(t)—第k个剩余微弱故障信号的频率。
因此,最终信号可表示为:
(12)
1.3 行星齿轮箱故障诊断
笔者采用局部均值分解方法(local mean decomposition,LMD)获取行星齿轮箱微弱故障的时频信号,同时将其和希尔伯特变换(Hilbert transform)相结合,即可获取信号的时频分布[18]。
结合时频分析方法如下:
当得到行星齿轮箱振动信号的微弱故障信号分量后,需对各个微弱故障信号分量实行Hilbert变换处理[19],可得计算公式为:
(13)
式中:PFp(t)—经过Hilbert变换处理的微弱故障信号分量;t—采样周期。
同时,组建解析信号的具体计算公式为:
(14)
式中;xp(t)—解析信号。
通过式(14)获取信号的时频谱如下:

(15)
式中:H(ω,t)—信号的时频谱。
结合以上分析,笔者采用局域均值分解方法对行星齿轮箱实行故障诊断处理[20]。
详细的故障诊断流程如图2所示。
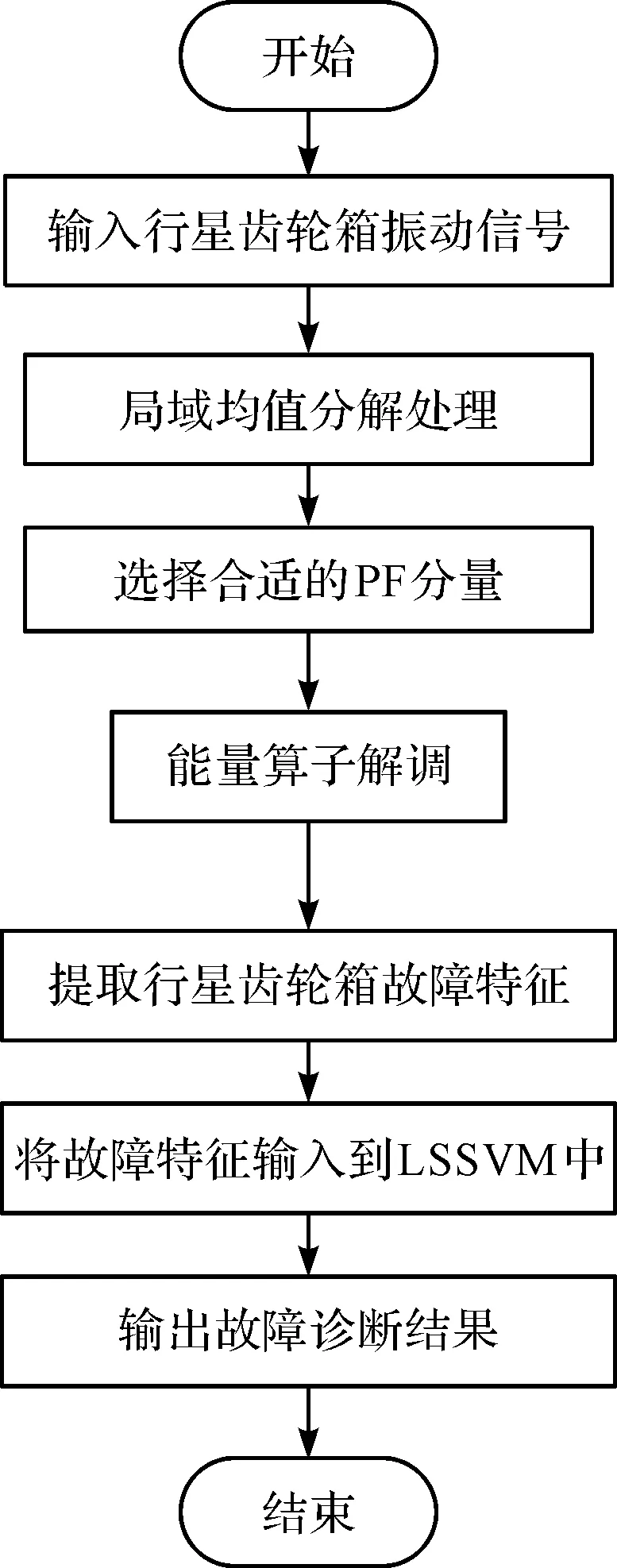
图2 行星齿轮箱故障诊断流程
行星齿轮箱故障诊断具体步骤如下:
(1)在随行星齿轮箱故障信号进行去噪处理后,需对振动信号展开局域均值分解处理[21];
(2)根据分解结果选择合适的微弱故障信号分量;
(3)通过步骤(2)获取乘积函数;
(4)获取微弱故障信号分量对应的幅值和相位调制;
(5)提取行星齿轮箱故障特征[22-25];
(6)将提取到的特征输入到最小二乘支持向量机(LSSVM)中,输出行星齿轮箱故障诊断结果,最终实现齿轮箱的故障诊断。
2 仿真实验
为了验证上述故障诊断方法的有效性,接下来,笔者展开实验测试分析。
此处,笔者系统以LABVIEW为基础搭建了仿真实验平台。
行星齿轮箱试验台结构原理如图3所示。

图3 仿真实验平台原理图
该实验平台由输入编码器、磁粉制动器、行星齿轮箱和编码器组成。笔者设置齿轮箱采样点为5 000个,采样频率20 kHz,每10 min采样一次,每次采样10 s;驱动轮是一个整体齿轮轴,行星轮齿数为20,行星轮个数为3个,无源轮齿数为70;齿轮啮合频率为700 Hz。
为了准确描述相关信号,笔者优先对行星齿轮箱信号实行局域均值分解处理。分解所得实验结果,即行星齿轮箱仿真信号经LMD分解后的时域波形及频谱图,如图4所示。
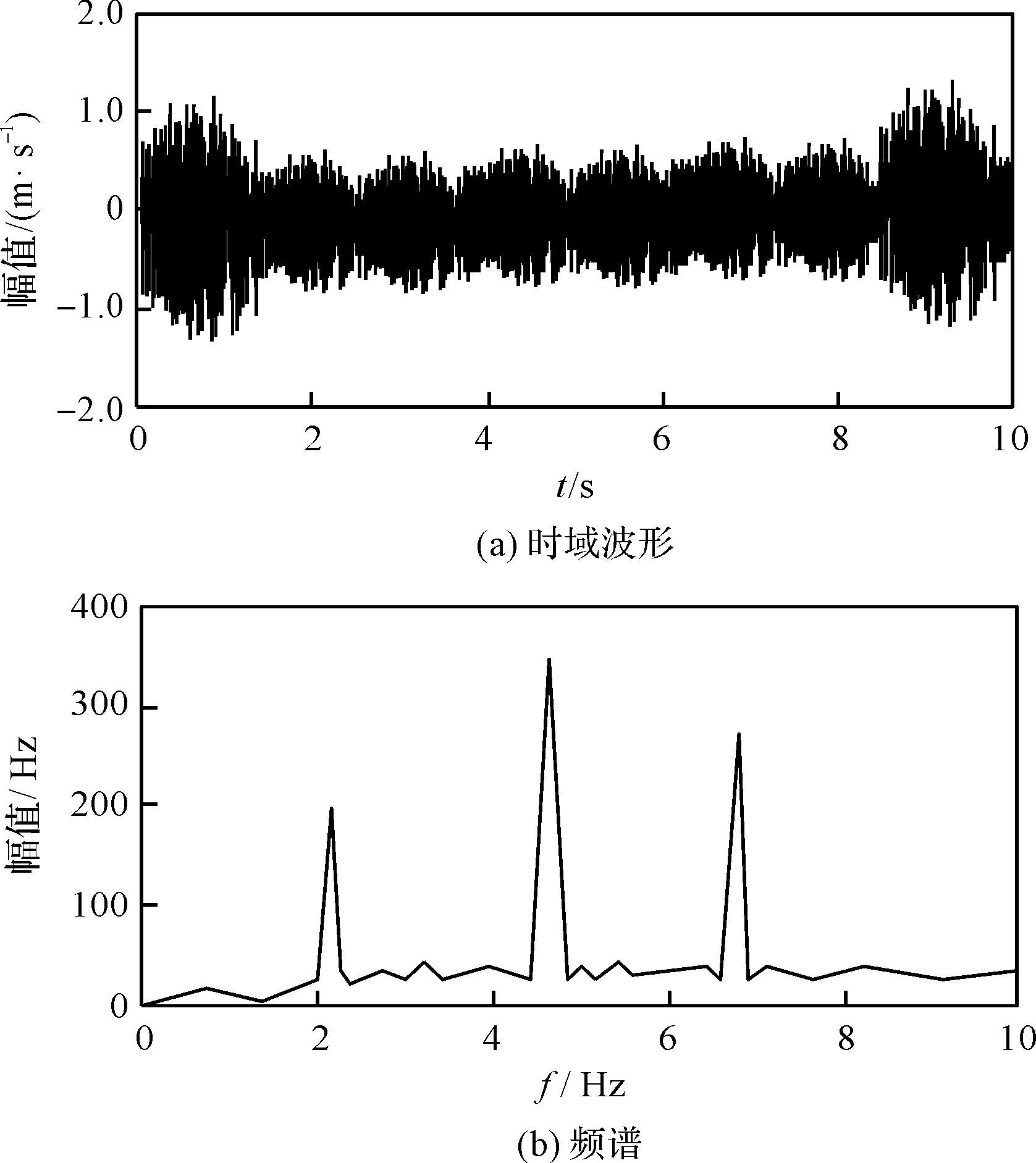
图4 LMD分解后的时域波形及频谱图
由图4可知:采用上述诊断方法对行星齿轮箱仿真信号分解后,得到的行星齿轮箱的时域波形稳定,幅值在-1 m·s-1~1 m·s-1之间波动;一级啮合频率为192 Hz、二级啮合频率339 Hz、三级啮合频率为281 Hz,二阶啮合频率处幅值增幅最大,可判断二级啮合齿轮上发生故障。
齿轮一级转动、二级转动、三级转动的绝对旋转频率分别为0~18 Hz、18~22 Hz、19~23 Hz。当信号包络谱频率在0~4 Hz范围内时,行星齿轮箱的时域幅值由0.2 m·s-1降至0.01 m·s-1。
根据图4分析,笔者获取了行星齿轮箱齿轮特征频率变化情况,如表1所示。

表1 行星齿轮箱的特征频率变化
笔者分别采用3种不同方法提取行星齿轮箱的故障信号特征。
不同方法下的行星齿轮箱故障诊断对比分析结果,如图5所示。

图5 不同方法行星齿轮箱故障诊断结果对比
其中,图5(a)所示为行星齿轮箱异常部分详细的实验测试结果。
由图5可知:行星齿轮箱存在微弱异常信号及强异常信号;在3种故障诊断方法中,基于局部均值分解(LMD)方法可准确提取出齿轮箱的故障振动微弱异常信号及强异常信号,而另外两种方法提取的特征结果精准度不高,无法准确诊断其故障特征。
由此可见,采用基于LMD的方法进行行星齿轮箱故障诊断可以达到较高精度。
3 结束语
为了有效克服传统齿轮箱故障诊断方法的弊端,笔者提出了一种基于局域均值分解的行星齿轮箱故障诊断方法,即采用平移非变量小波降噪技术对行星齿轮箱故障信号进行降噪处理,利用局域均值分解对各振动信号进行分解,获取其幅度和相位调制信息,从而实现了对行星齿轮箱故障信号的精确识别。
研究结论如下:
(1)基于LMD的方法得到的行星齿轮箱仿真信号时域波形稳定,幅值在-1 m·s-1~1 m·s-1间波动;
(2)二阶啮合频率为339 Hz,增幅最大,可判断二级啮合齿轮上出现故障;
(3)基于LMD的方法可用于准确诊断行星齿轮箱故障、精准定位行星齿轮箱故障位置。
基于LMD的方法能够准确判断行星齿轮箱故障位置,但在故障定位效率方面仍有提升空间。因此,在接下来的工作中,笔者将以故障定位效率为研究对象,进一步完善基于局域均值分解的行星齿轮箱故障诊断方法。

