汽车智能制造中协作机器人的任务分配问题研究
李润泽,钱仕德,逯汉宁
(1.北京奔驰汽车有限公司,北京 100176;2.农业农村部国际交流服务中心,北京 100125)
0 引 言
近年来,人工智能的快速发展促进了工业、制造业的进步,开启了智能机器人协作生产的新时代。然而,目前协作机器人仅能完成简单、重复且认知负荷低的任务,无法完全替代生产制造过程中的人力劳动。因此,围绕该问题,黄海丰等就机器人与人执行协作的高效性进行了讨论[1];鞠兴全等将协作机器人应用于航天领域,并与人协同工作,提升了整体工作效率[2];庞党锋等基于协作机器人,对计算机装配工作站进行了设计与仿真,调试时间和成本,提高了生产效率[3];郭鸿志等为实现复杂任务的资源分配和优化,通过以最小化任务处理时延为目标,建立子任务执行时序约束、响应时间约束、任务卸载约束,并利用双层博弈近似计算卸载算法进行求解,提高了协作机器人对复杂任务处理时延的性能[4];季金华等为实现物资协同配送优化,以最低配送成本为目标,采用嵌入改进节约里程算法对无人机和卡车运输进行规划,实现了无人机与卡车的协同配送[5]。通过上述研究看出,协作机器人广泛应用于各个领域,大大提高了制造效率。
汽车作为生活中必不可少的交通工具,其零部件的装配复杂性高,部分仍停留在人工装配阶段。为实现汽车智能装配与制造,通过充分分析协作机器人与人工合作,本文提出一种汽车差速器装配任务的智能分配方案,可在提高装配效率基础上,降低制造成本。
1 装配复杂性度量
装配复杂性度量可量化装配过程中协作机器人分配任务的复杂性。根据汽车智能制造减速器中装配线的特点,其复杂度可通过工艺深度、操作过程和认知过程复杂性进行衡量,具体如图1所示[6]。
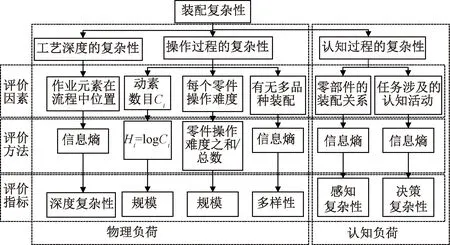
图1 装配复杂性框架模型
(1)工艺深度复杂性
工艺深度复杂性HD可利用信息熵进行度量,其计算方法如下[7]:
(1)
pi=ri/(r1+r2+r3)
(2)
式中:ri为每个作业元素之间的关联关系;r1、r2表示与本作业元素为前序和后续的个数;r3表示与本作业元素并行的个数。
(2)操作过程复杂性
操作过程复杂度由规模因子、难度因子、状态多样性因子决定。其中,规模因子的计算方法如下[8]:
Hi=lgCi
(3)
式中:Hi表示第i个作业元素规模因子;Ci表示第i个作业元素动素数。
难度因子KC通过式(4)计算:
(4)
作业元素的相对操作难度影响因素较多,主要包括定位、紧固、固定等,且呈现出非线性关系。因此,本文采用神经网络建立评价模型,实现对所有作业元素的相对操作难度[9]。
多样性因子DR可根据信息熵进行描述,如下:
DR=-p·lgp
(5)
式中:p=1/n,n表示需要装配的产品类型数。
综合规模因子、难度因子和多样性因子,可得到操作过程复杂度的计算方法如下:
HP=KC(1+DR)H
(6)
式中:HP表示操作过程复杂度;H表示规模因子;KC表示难度因子;DR表示多样性因子。
(3)认知过程复杂性
认知过程是一个集信息输入、处理和输出为一体的复杂过程,包括感知过程和决策过程。其中,感知过程即信息数量。设Xi工序存在m个作业元素,那么作业元素之间的关系复杂度可表示:
(7)
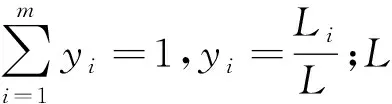
设整个装配过程含有i个作业元素,则感知过程的复杂度可表示:
(8)
式中:H(X)表示感知过程复杂度;H(Xi)表示每个作业元素感知过程复杂度。
决策过程包括信息处理与输出。假设Xi工序存在m个作业元素,那么认知活动数量的复杂度可表示:
(9)
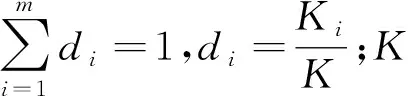
设整个装配过程中含i个作业元素,则决策过程的复杂度可表示:
R(X)=R(X1)+R(X2)+…+R(Xm)
(10)
综合式(8)和式(10),可得到认知过程复杂度:
HC=H(X)+R(X)
(11)
式中:HC表示认知过程复杂度;H(X)表示感知复杂度;R(X)表示决策复杂度。
最后,综合所有装配复杂性,可得到整个装配复杂性的计算方法,如下:
HT=HD+HP+HC
(12)
式中:HT表示装配复杂度;HD、HP、HC分别为工艺深度、操作过程和认知过程复杂度。
2 汽车差速器智能装配任务规划
针对协作机器人在汽车减速器智能装配中的任务,本文提出首先计算人工和协作机器人的装配成本,然后设计多层次任务分配模型,并以装配复杂性为指标进行任务分配,最后采用遗传算法对分配模型进行求解,实现人与协作机器人装配任务的优化分配。
2.1 装配任务分配模型构建
2.1.1 模型假设
为便于模型构建,进行以下假设:
(1)任务完成时间由分配的是机器人还是工人决定,其对应值确定;
(2)每个任务必须得到分配;
(3)忽略任务操作时的安装时间和任务制品库存问题[10];
(4)为保证任务执行的连续性,应尽量减少任务切换次数。
2.1.2 模型构建
根据上述模型假设与汽车差速器装配任务,将任务分配模型框架设计为图2。
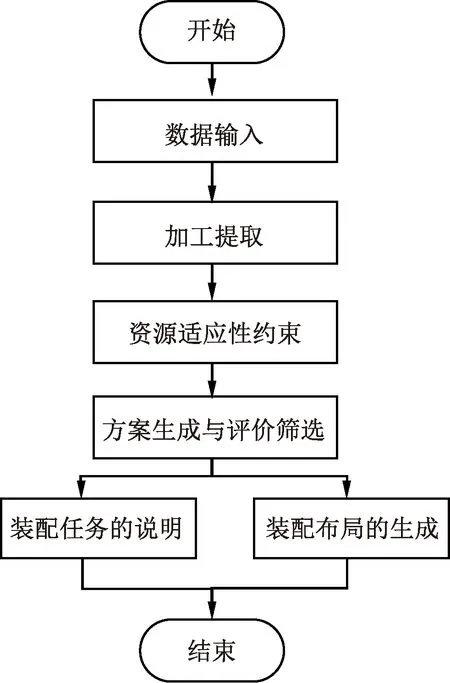
图2 装配任务分配模型框架
为生成和筛选出合理的装配任务分配方案,应尽量确保时间利用均衡率TUR尽可能高,以节约成本;工人负荷均衡率HBR越大,越能保证工人生理与心理的平衡;机器人任务认知负荷ACCR低于工人任务认知负荷ACCH,以确保任务分配合理;平衡滞延时间BD最小,以提高任务执行效率。具体如下[11]:
(13)
式中:Ti表示劳动资源i的工作时间;Timax表示最长劳动资源工作时间;n表示所有劳动资源;HT(h)表示每个工人承担任务装配复杂度;H表示工人总数;HTmax(h)表示所有工人中承担装配复杂度最大的值;ACC为平均认知过程复杂度;HC(r)、HC(h)分别为协作机器人r和工人h承担任务认知过程复杂度;R、H分别为协作机器人和工人总数;BD为平衡滞延时间;C表示需求节拍;Pn表示n个劳动资源含量时间;n表示所有劳动资源。
2.2 装配任务分配目标函数
在协作机器人辅助人工进行汽车差速器智能装配过程中,装配任务分配的目标是使时间利用均衡率和工人负荷均衡率尽可能大,即:
TUR(h,r)≥α
HBR(h,r)≥β
式中:α、β分别表示限定最小时间利用均衡率和工人负荷均衡率。
同时保证工人任务的平均认知过程复杂度高于协作机器人,即:
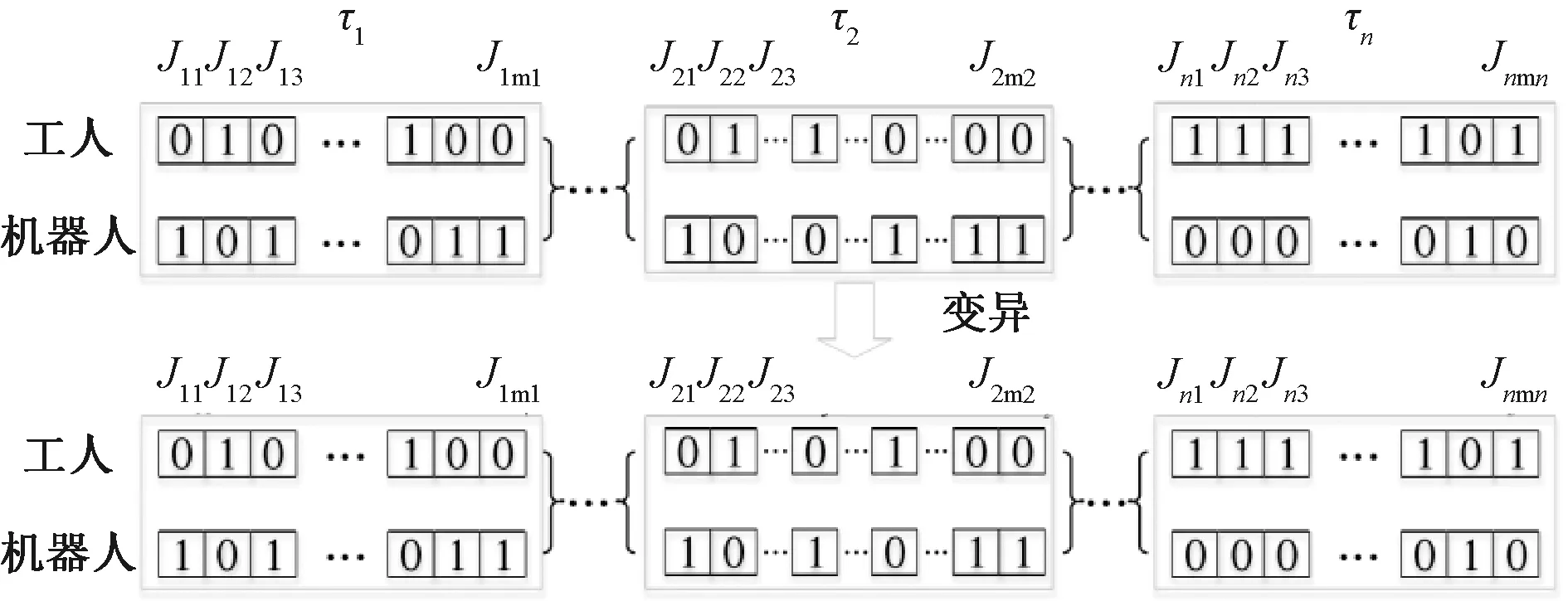
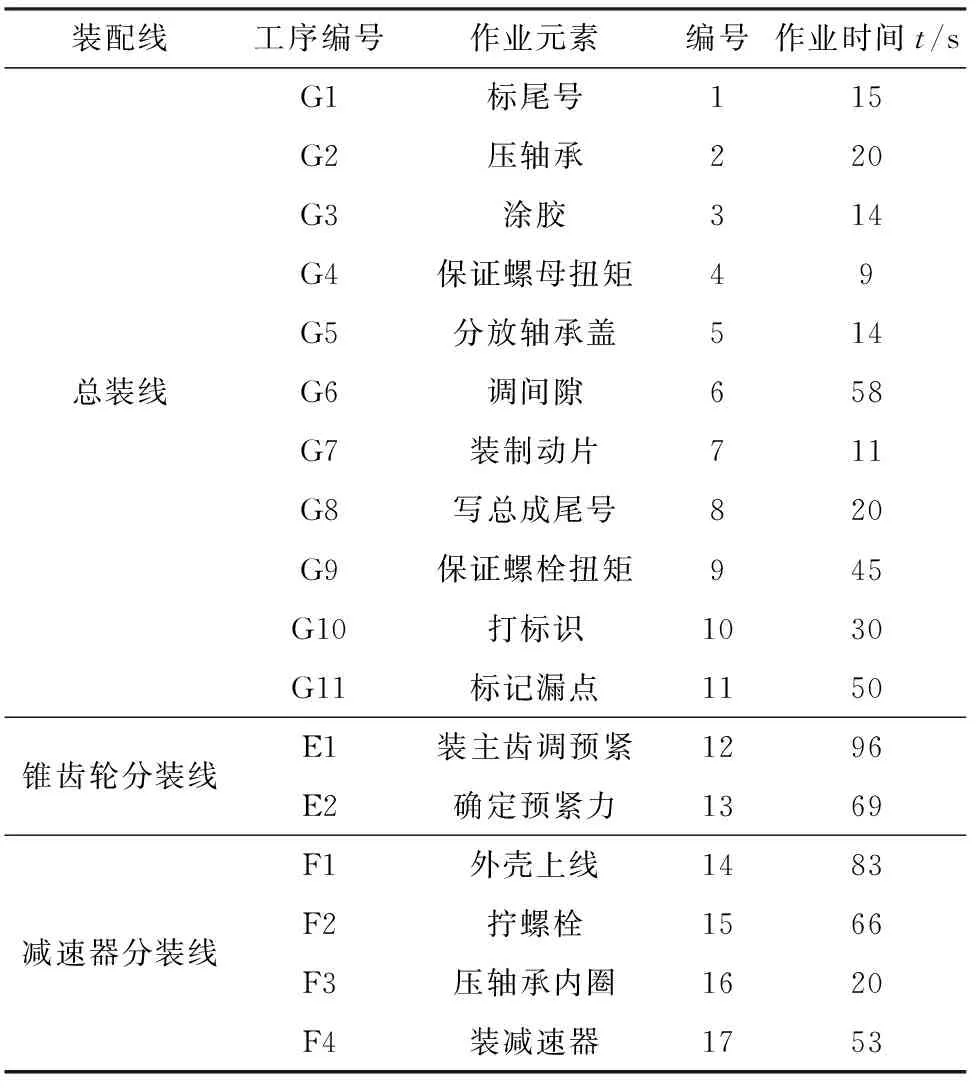
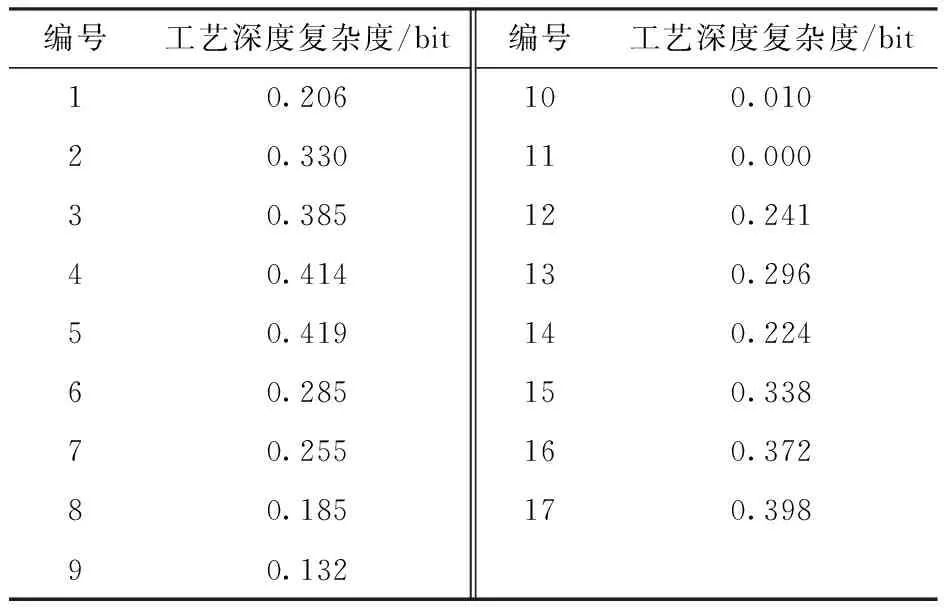
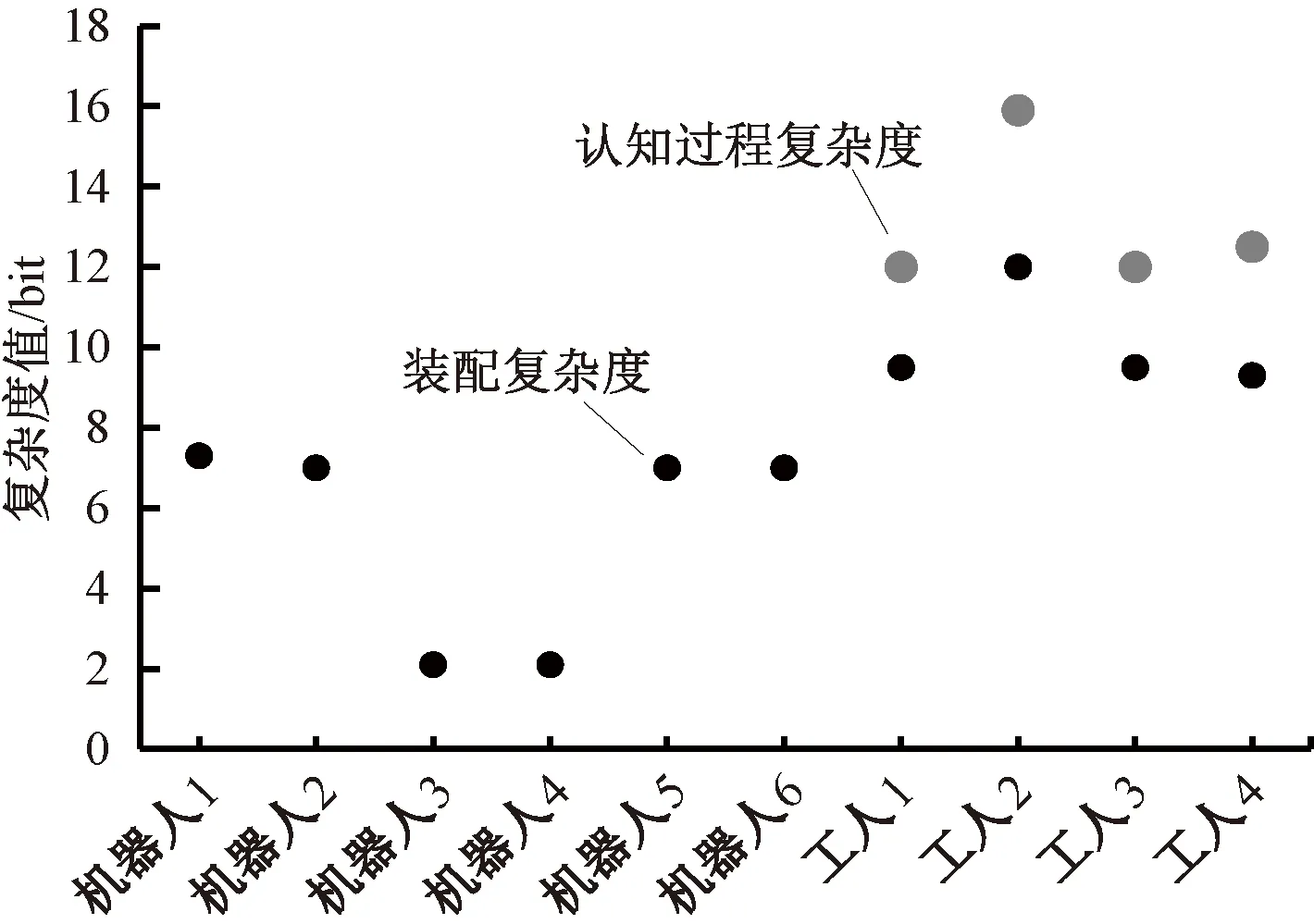
ACCR(h,r) 最终保证平衡滞延时间最小,满足[12]: 2.3.1 协作模式 采用遗传算法对上述目标进行求解。确定协作机器人与工人的协作模式,设存在τ个任务分配给r个协作机器人和h个工人,则协作机器人与工人的协作模式可表示[13]: P(h,r)=[τ,h,r,ε,c] 式中:P(h,r)为资源数量及各自任务分配集合;[τ,h,r,ε,c]表示输入资源和生产信息集合,τ={τ1,τ2,…,τn}表示生产某一产品所需n个工序;ε={εr,εh}表示任务操作时间;c={HD,HP,HC}表示装配复杂度。 2.3.2 任务编码 初始化种群和对任务操作模式进行编码、交叉、变异等操作。设生产某个产品τ所需n个工序,每个工序中含多个作业元素,则: τ={J11,J12,…,J1m1},{J21,J22,…,J2m2},…, {Jn1,Jn2,…,Jnmn} 图3 编码方式 随机选取任务进行交叉和变异操作,具体如图4、图5所示。 图4 交叉操作 图5 变异操作 2.3.3 适应度函数构建 根据适应度函数计算适应度,确保装配平衡滞延时间最短[14],本文适应度函数设计: f(BD)=1 000/BD 为验证上述采用遗传算法求解的协作机器人与工人在汽车减速器智能装配任务分配方案的有效性,选用某企业汽车智能制作过程中减速器装配线作为研究对象。该装配线包括一条总装线、一条差速器分装线和一条锥齿轮分装线,由18个工人进行34个作业,每个工人工位操作统计如表2所示,装配线总体布局如图6所示[13]。 表2 工位操作统计 图6 减速器装配线布局与流程 3.2.1 工艺深度复杂度 汽车智能制造减速器装配线中,工艺深度复杂度可根据式(1)及装配流程(图6)进行计算,计算结果如表3所示。 表3 工艺深度复杂度 3.2.2 操作过程复杂度 操作过程复杂度的规模可通过移动物体、装配、定位、拆卸的数量来确定。每个作业规模因素规模统计如表4所示。 表4 各作业元素规模统计 根据相对难度统计方法,各作业元素相对难度如表5所示。 表5 各作业元素相对难度统计 装配过程中的多样性可根据式(6)计算,得到多样性值为0.150 5。 综合装配过程中的规模、相对难度、多样性,并根据式(7)可计算得到整个操作过程中的复杂度,如表6所示。 表6 装配操作过程复杂度统计 3.2.3 认知过程复杂度 汽车智能制造减速器装配线中,认知过程复杂度由感知复杂度和决策复杂度决定,而感知复杂度由作业前后各作业元素之间的关系决定[14]。利用各作业元素之间的关系计算得到的感知复杂度,如表7所示。 表7 各作业元素感知复杂度统计 决策复杂度可从观察、计划、解释、执行4个阶段进行计算,计算结果如表8所示。 表8 决策复杂度统计 综合感知复杂度和决策复杂度,可得到认知过程复杂度,如表9所示。 表9 认知过程复杂度统计 最后,结合工艺深度复杂度、操作过程复杂度和认知过程复杂度,可得到整个汽车智能制造中减速器装配线各作业元素的装配复杂度,如表10所示。根据表10,即可设计实现汽车智能制造中减速器装配线人与协作机器人的任务分配。 表10 各作业元素装配复杂度 利用协作机器人辅助人类进行汽车智能制造的目的,一方面是最小化平衡滞延时间,另一方面是使机器人承担简单重复的工作,同时确保机器人与人承担工作时间均衡。首先对输入数据进行处理,设置装配线街拍C=106 s,总加工周期T=1 064 s。由此可得到工作站至少需要10个才能满足需求,故假定该装配线上协作机器人与人类的总资源数为10。 根据人机协作属性计算方法[15],计算各作业元素人机协作属性,如表11所示。当人机协作属性超过50%,则该任务可由协作机器人或人类完成,反之,该任务只能由人类完成。 表11 人机协作属性评价结果 最后,为确定协作机器人与人工数目,采用每小时成本作为约束进行确定。根据式(12),可计算得到每项成本,并将人机协作每小时单位成本与传统装配单位成本进行比较,结果如表12所示,单位成本随协作机器人数量变化如图7所示。由表12可知,相较于传统全部人工进行装配,采用协作机器人辅助的人机协作装配成本每小时降低了9.40元,为每小时1 040.73元。 表12 每项作业成本 图7 单位成本随协作机器人数量变化 由图7可知,随着协作机器人数量的增多,减速器制造单位成本逐渐降低。从长远来看,使用协作机器人辅助人工装配汽车减速器,可节省大量成本。 (1)任务分配方案生成 采用visual C++语言编写程序生成任务分配方案。首先初始化函数和数据,计算各作业元素装配复杂度,然后利用遗传算法进行求解,最后判断求解结果是否满足设计要求,并对认知复杂度和平衡滞延时间进行优化,即可生成任务分配方案。 (2)最佳分配方案确定 为使人机协作效果达到最好,还需对生成的任务分配方案进行筛选。首先,不限制时间利用均衡率和工人负荷均衡率,得到不同组合下协作机器人任务认知复杂度,如图8所示。由图8可知,随着协作机器人数量的增加,其承担任务的认知复杂度逐渐增大。 图8 协作机器人承担任务认知过程复杂度趋势 然后,限制时间利用均衡率和工人负荷均衡率大于80%,并以最小化平衡滞延时间为目的,对任务分配方案进行筛选。表13为不同组合方案时协作机器人任务认知过程复杂度。由表13可知,当6台协作机器人和4个人工搭配时,机器人任务认知过程复杂度最低。因此,采用6台协作机器人与4个人工的任务分配方案。 表13 限制参数后机器人任务认知过程平均复杂度 采用6机4人的任务分配方案时,分配结果如表14所示。此时,时间利用均衡率为83%,工人负荷均衡率为84%,平均滞延时间为93 s,协作机器人与工人的装配复杂度分布如图9所示。由图9可知,在该任务分配方案下,协作机器人与工人装配复杂度差异明显,工人承担的任务均衡且复杂度更高,说明该方案充分利用了人类与协作机器人的优势,将认知过程复杂度高的任务分配给人类,将重复的认知过程复杂度低的任务分配给协作机器人,提高了汽车智能制造中装配线的鲁棒性,保证了生成的稳定性,有利于应对生产过程中的突发情况,方案合理。 表14 6机4人任务分配方案 图9 协作机器人与工人装配负荷分布图 为更好地展示方案的合理性,将人机协作装配任务分配方案结果通过甘特图进行可视化,可视化结果如图10所示,其中线段表示人机协作期间计划和实际完成装配任务的情况。由图10可知,6机4人的人机协作装配任务分配方案不一定是传统意义上的最佳方案,但从整体来看,具有一定的优越性。 图10 人机协作装配任务分配甘特图 根据所设计的任务分配方案,应用于汽车智能制造减速器装配线生产,可得到协作机器人与人工的新布局方案,如图11所示。 图11 人机协作的智能汽车减速器装配线布局 为验证本方法的优越性,实验对比了人机协作任务分配方案与文献[15]方案,结果如表15所示。由表15可知,本方案的认知过程复杂度和装配复杂度更低,具有一定的优越性。 表15 方案对比 综上所述,本文的协作机器人辅助汽车差速器智能装配方案,通过构建装配复杂性度量模型对装配复杂性进行量化,并以其为指标,采用遗传算法求解协作机器人装配任务,得到6台协作机器人和4个人工的装配方案,实现汽车差速器智能装配与装配任务的合理分配,有效提高了生产效率,降低了汽车差速器制造成本。相较于传统汽车差速器装配全部采用人工的方案,6机4人的装配方案每小时单位成本节约了9.40元,为每小时1 040.73元,具有较大的优势。2.3 目标函数求解


3 实例验证
3.1 实例背景

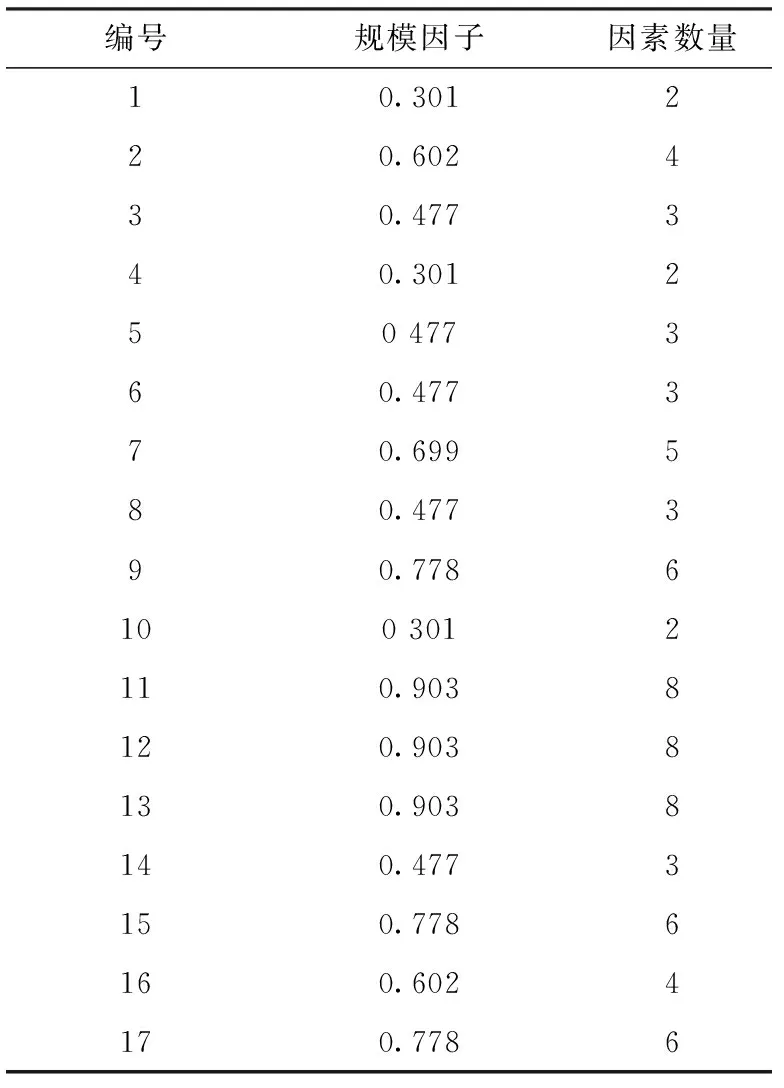
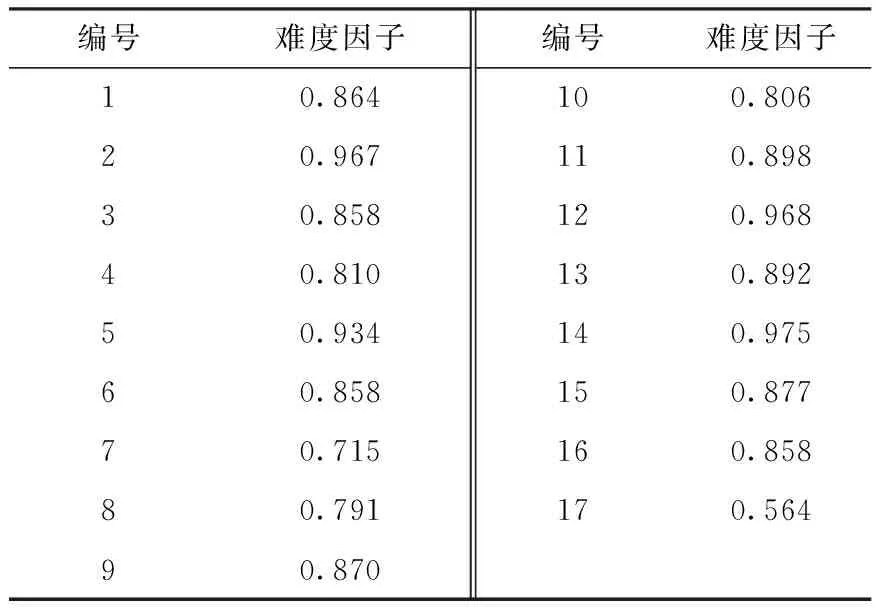
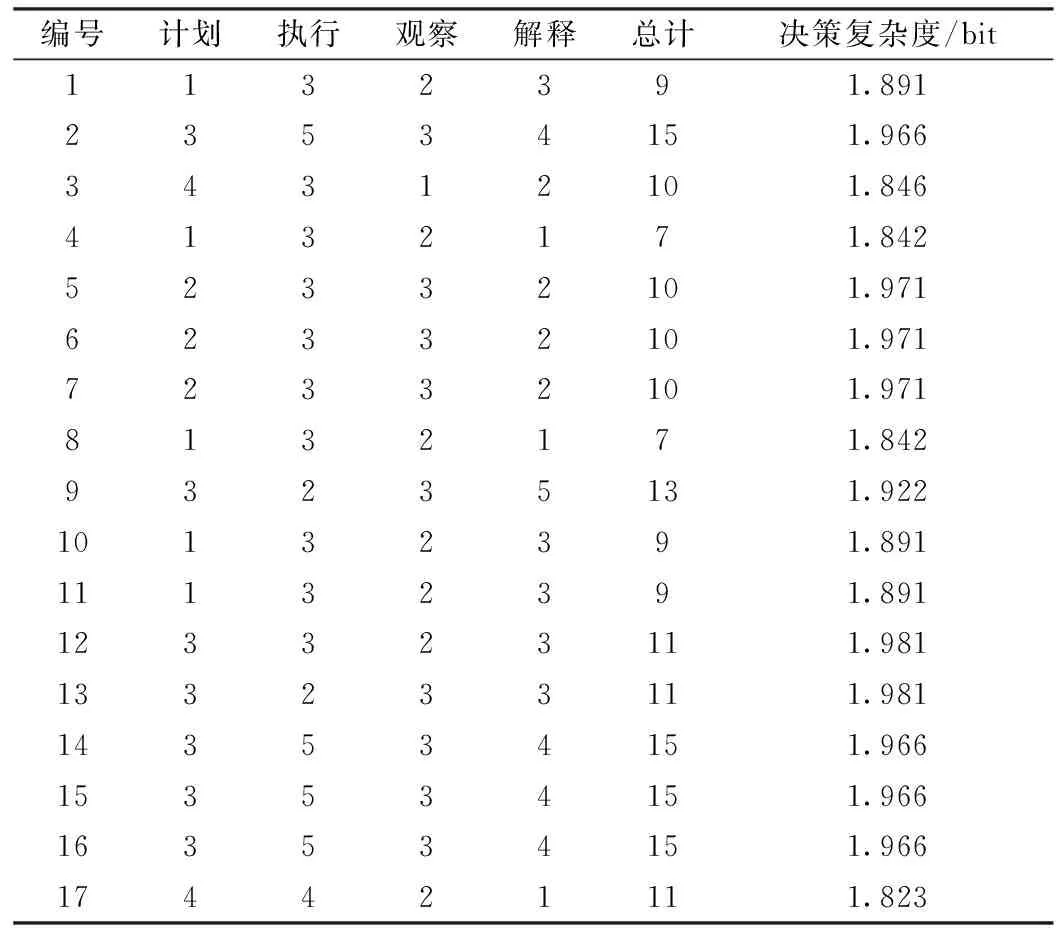
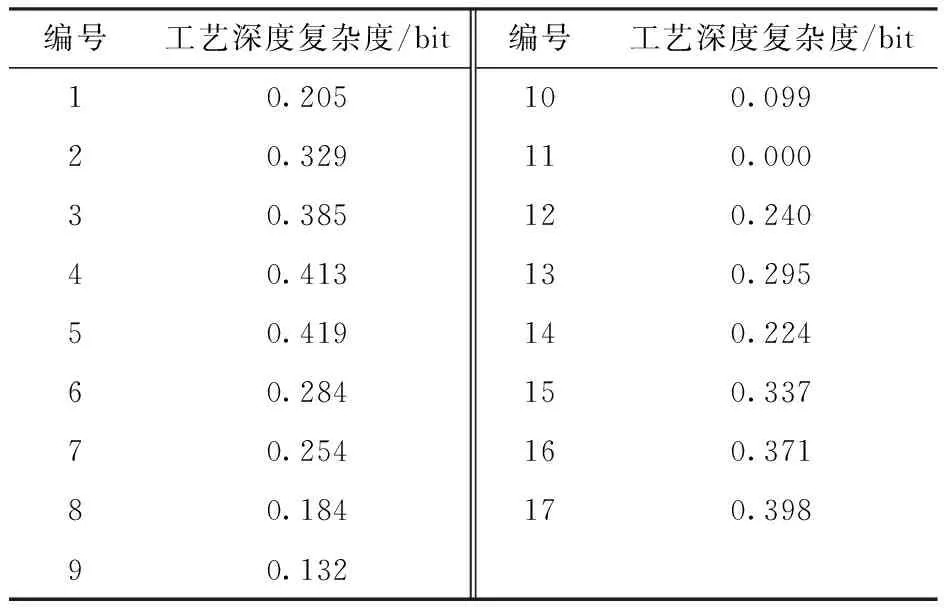
3.2 装配复杂性计算



3.3 装配任务分配
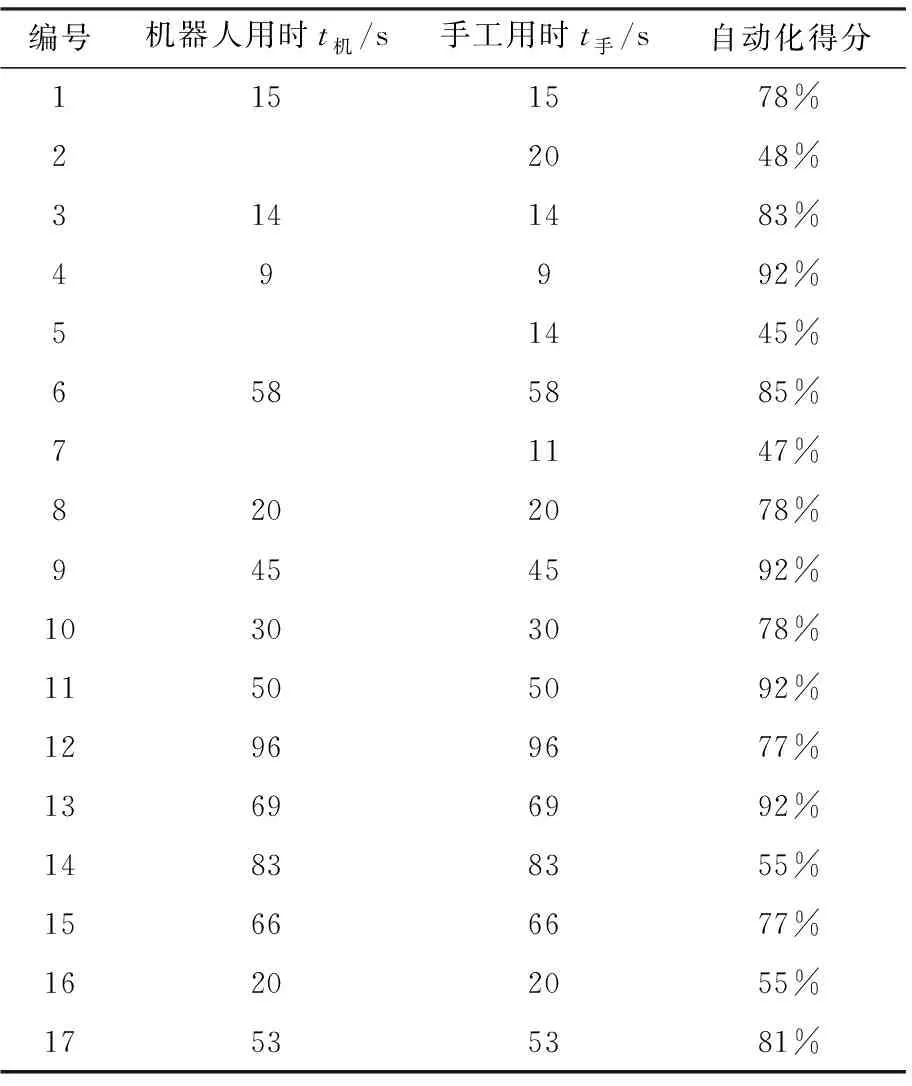
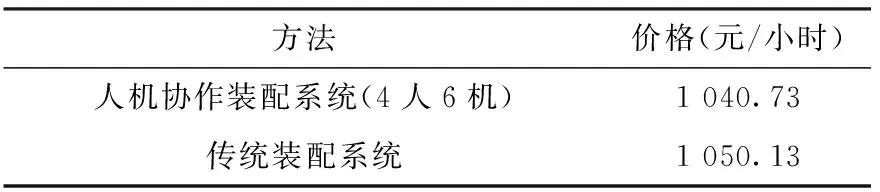
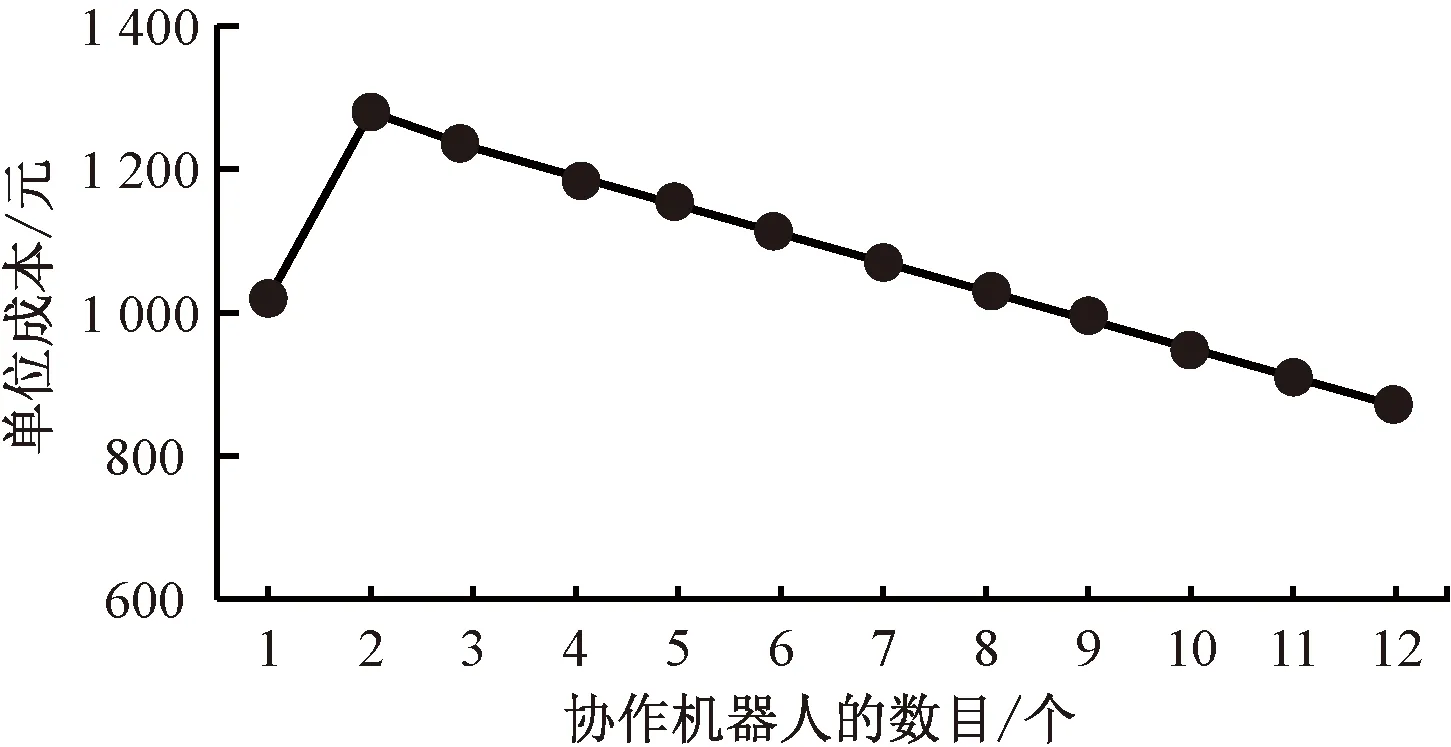


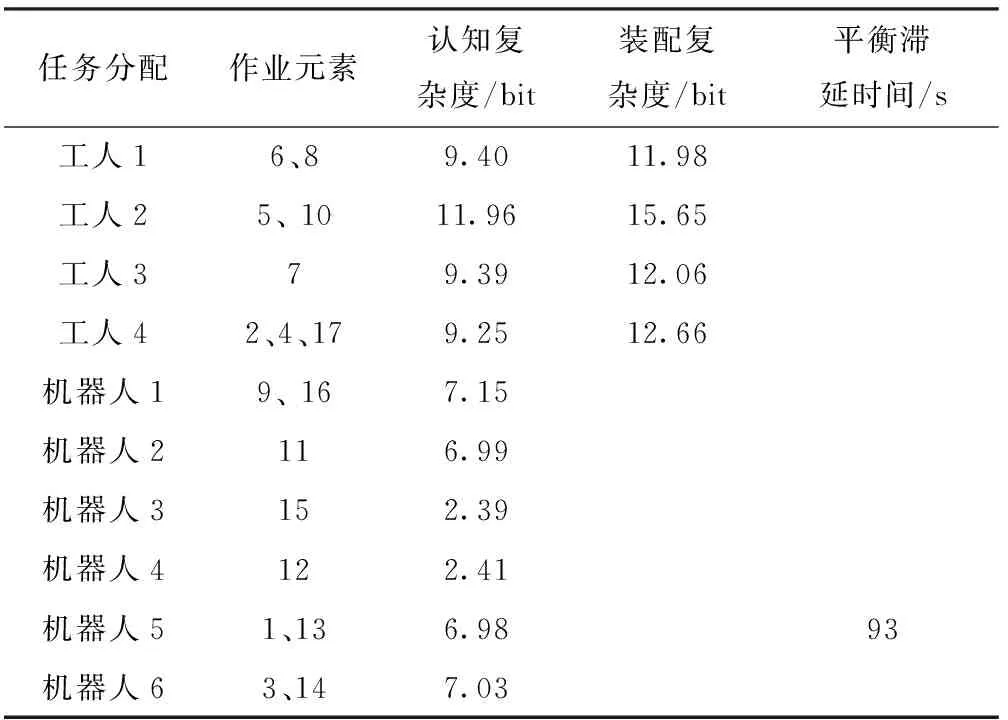


3.4 方案对比

4 结 语