高速实心转子感应电机的转子谐波涡流损耗的分离和提取
狄 冲,王路尧,鲍晓华
(1.合肥工业大学 电气与自动化工程学院,合肥 230009; 2. 安徽大学 高节能电机及控制技术国家地方联合工程实验室,合肥 230601)
0 引 言
目前,主要有三种电机适用于高速领域并应用于实际工程,它们分别是感应电机、永磁同步电机和开关磁阻电机[5-7]。近些年,同步磁阻电机也逐渐开始应用于高速领域[8-9]。然而,前三种电机相较于最后一种电机具有更长远的应用历史和更高的效率,因此前三种电机仍为现今研究热点,其中高速感应电机凭借其加工简单、机械强度高、可靠性好以及成本低廉等优势,在高速领域的研究价值和应用前景变得尤为突出。
对于高速感应电机而言,转子外圆最大线速度受转子结构拓扑影响较大。根据文献[2]和文献[3],实心开槽转子、实心鼠笼转子、叠片转子和光滑带护套实心转子对应转子外圆最大线速度分别为204 m/s,236 m/s,290 m/s和367 m/s。然而,文献[5]和文献[10]一致认为在转子外圆线速度高于200 m/s的情况下,电机设计过程中采用实心转子能够保证电机更为安全的运行。但是,实心转子电机较其他结构拓扑的感应电机而言,其电磁性能较弱,这是因为实心转子具有较强的端部效应,导致转子功率因数偏低和电机效率偏低。
当高速感应电机采用实心转子后,一般都具有较好的转子机械强度,但其转子感应涡流引起的损耗通常都较为严重。因此,大量的研究重点关注转子感应涡流损耗的预测与抑制。文献[11]详细对比了采用实心转子和鼠笼叠压转子的感应电机转子损耗,其数据表明,在额定工况下前者比后者的转差损耗高出近0.7%。文献[12]指出,当采用开槽转子,其开槽深度为40%~50%转子半径时,电机效率和功率将处于较高区间范围内。文献[13]提出了采用考虑时间和空间谐波的改进解析法来预测转子感应涡流损耗,并通过实验验证了解析模型的正确性,但该方法忽略了齿谐波的影响。针对这个问题,文献[14]提出了能够考虑齿谐波影响的高速实心转子感应电机转子感应涡流的快速计算方法,然而其忽略了转子饱和的影响。文献[15]和文献[16]提出了一种“虚拟永磁谐波电机”的概念,计算转子感应涡流损耗,将气隙中各项谐波以及转子饱和情况都考虑进来,并成功定量分离了各谐波成分所引起的谐波涡流损耗。
在抑制实心转子感应涡流损耗方面,转子材料的选取也至关重要。通常为了减少转差损耗,可以选用低电阻率的材料。文献[17]详尽分析了采用Fe52、C15、Fe-Cu和Fe-Si(Consumet)4种材料的高速实心转子感应电机所对应的整机效率,采用上述4种材料的高速实心转子感应电机较其他材料的高速感应电机具有更高的效率。此外进一步研究发现,Fe52、C15和Fe-Si(Consumet)在电磁性能和机械强度上都具备较好的性质。
本文以一台380 V,1 MW,12 000 r/min高速实心转子感应电机为主要研究对象,以虚拟永磁谐波电机模型为切入点,采用混合激励和冻结磁导率方法分别对转子谐波涡流损耗进行分离和提取。通过上述方法,不仅获得了气隙谐波磁场在实心转子表面所引起的谐波涡流损耗,还得到了高频感应涡流的分布,为后续对转子谐波涡流损耗进行有效抑制提供了理论基础。
1 高速实心转子感应电机的气隙谐波磁场分析
1.1 电机主要参数和性能分析
本文以一台380 V,1 MW,12 000 r/min高速实心转子感应电机为主要研究对象,对其进行有限元建模,并进一步分离提取转子谐波涡流损耗,其主要设计参数如表1所示。其中,定子材料采用M270-35A,转子材料采用实心钢S355,其180 ℃下的电导率为2.22×106S/m。

表1 高速实心转子感应电机主要设计参数
图1显示了优化设计后的高速实心转子感应电机在额定工况下的磁密和磁力线分布。从图1中可以看出,实心转子上开了空槽,增加了转子表面横向阻抗,导致气隙磁场顺利透入转子内部,从而产生电磁转矩,使得实心转子利用率得到提高。此外,为了能够同时兼顾电机电磁性能和转子机械强度。图1中的实心转子槽深为42 mm,约占转子半径的36.7%,符合文献[12]中槽深的推荐范围。

图1 额定工况下电机磁密和磁力线分布图
表2列举了高速实心转子感应电机在额定工况下的主要性能指标。其中在额定转矩800 N·m时,采用二维瞬态场仿真计算得到额定转差率为0.003 8。而电机实际运行中由于实心转子端部效应,一般转子电阻率会提升为原来的1.5至2倍,相应的转差率和转差损耗也将提升1.5至2倍。此外,表2 中的机械损耗和杂散损耗都按额定功率的0.5%进行初步估算。
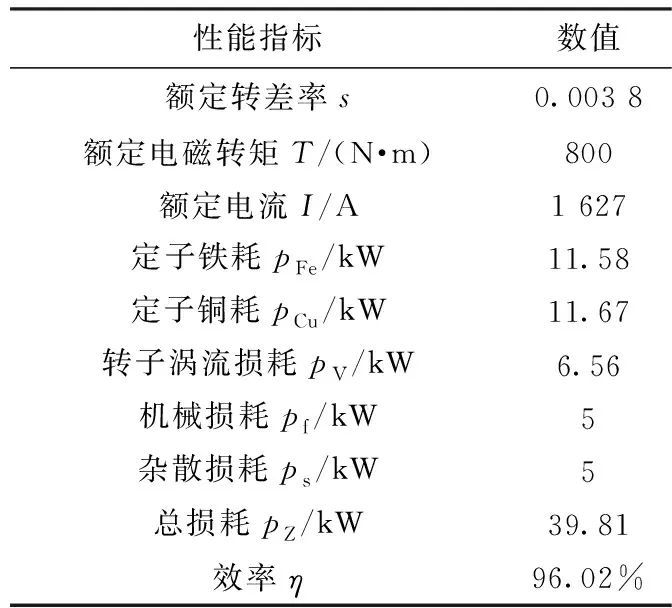
表2 高速实心转子感应电机额定工况下的主要性能指标
1.2 气隙谐波磁场的分离
高速实心转子感应电机在运行过程中,气隙磁场中含有较为复杂的谐波磁场,需要对谐波磁场进一步分离和提取才能对转子涡流损耗进行进一步的计算。气隙ν次谐波磁场可以表示:
(1)

根据气隙谐波磁场产生原因的不同,表3列举了气隙谐波磁场中的主要成分。表3中,阶次为p的气隙磁场为基波成分,其转速为同步转速;2mk±1项为相带谐波,其中k为正整数;kQs±p和kQr±p

表3 气隙谐波磁场主要成分
项分别为定子齿谐波和转子齿谐波。
由表3可以进一步发现,相带谐波和定子齿谐波所引起的定子侧频率皆为f,而基波和转子齿谐波所引起的转子侧频率皆为sf。该现象表明,沿时间轴对气隙谐波磁场作一维傅里叶分解,将无法精确区分相同频率不同阶次的谐波。同理,相带谐波和定子齿谐波同样具有一部分相同阶次的谐波。该现象表明,沿空间轴对气隙谐波磁场作一维傅里叶分解,同样无法精确区分不同阶次相同频率的谐波。
由式(1)可知,从数学形式上看,气隙谐波磁场可以看作是一时空变化的二元函数,由此可见传统一维傅里叶分解无法准确提取气隙谐波磁场。针对上述现象,将气隙谐波磁场沿时间和空间轴采用二维傅里叶分解,能够有效提取不同频率和不同阶次的谐波。二维傅里叶正向和逆向变换分别可以表示:
(2)
式中:f(x,y)为二维信号;F(m,n)为二维频谱,表示二维信号沿x方向频率m和沿y方向频率n处的频率。式(2)的第一行为二维傅里叶正变换,第二行为二维傅里叶逆变换。
此外,结合表3可以发现,基波和转子齿谐波在转子侧产生的感应频率皆为sf,而相带谐波和定子齿谐波在转子侧感应频率则为±f[1-ν(1-s)],因此转子侧产生的谐波损耗主要由定子侧谐波所引起的。
表4详细列举了采用二维傅里叶分解所提取的定子侧谐波磁场特性。从表4中可以看出,除基波以外,定子一阶齿谐波(阶次为-35)具有较高幅值,且由于采用短距绕组,-5和7阶谐波都得到了较好的抑制。

表4 定子侧谐波磁场特性
2 改进的虚拟永磁谐波电机模型
2.1 传统虚拟永磁谐波电机模型
为了精确定量分离并提取气隙磁场谐波在实心转子表面引起的谐波涡流损耗,可以采用虚拟永磁谐波电机模型对转子谐波涡流损耗进行分离,其构建步骤如下:
(1)仿真计算负载状态下高速实心转子感应电机并达到稳态,在气隙中间位置处提取如图2所示的气隙磁密分布的时空分布,并采用二维傅里叶分解提取气隙磁密谐波特性;

图2 气隙中间位置处所提取的气隙磁密时空分布图
(2)删除图1中电机二维有限元模型定子侧模型,仅保留实心转子侧模型,从而构成单独转子模型;
(3)在单独转子模型的气隙外缘(即原模型定转子气隙中间位置处)建立恒定磁场边界条件,实现反向构建表4中的气隙谐波磁场,用以激励实心转子,该恒定磁场边界在x和y为直角坐标系下的参数方程可以表述:
(3)
(4)依据步骤(3)中建立的模型,采用ν次谐波激励,仿真计算待模型达到稳定状态,获取最后一个电周期实心转子涡流损耗的平均值pν。
采用上述方法能够较为精确地反向构建气隙磁场谐波特性,从而采用谐波磁场激励实心转子并获取转子表面相应的谐波损耗。图3显示了采用虚拟永磁谐波电机模型构建的-5次谐波磁场波形。从图3中可以看出,构建的谐波磁场模型具有较高的正弦性,其幅值为0.004 82 T,和表4中的目标磁场幅值0.004 8 T相比,误差较小。

图3 采用虚拟永磁谐波电机模型构建的-5次谐波磁场波形
虚拟永磁谐波电机模型能够较为精确地反向构建气隙谐波磁场,并且用其建立的谐波磁场激励实心转子,能够获取转子表面谐波涡流损耗pν:
(4)
式中:σ为实心转子材料的电阻率;Г为实心转子所在的二维平面;lef为实心转子有效长度;Jνz为ν次谐波磁场在转子表面引起的沿z向(轴向)感应涡流,该涡流在实心转子表面的透入深度δν可以表示:
(5)
式中:μ0为真空磁导率;μr为实心转子表面相对磁导率。
从式(5)可以看出,谐波涡流在实心转子表面的透入深度主要取决于谐波阶数、谐波涡流感应频率、转子电阻率以及转子表面相对磁导率。实心转子材料为实心钢S355,其具有非线性的B-H曲线,因此考虑在不同负载情况下的谐波涡流透入深度,是计算实心转子表面谐波涡流损耗的关键。
2.2 采用混合激励的虚拟永磁同步电机模型
采用混合激励的虚拟永磁同步电机模型是一种有望解决精确考虑负载情况下谐波涡流透入深度的计算模型,其构建逻辑如图4所示。从图4中可以看出,采用混合激励的虚拟永磁谐波电机模型提取转子谐波涡流损耗需要构建2个虚拟永磁谐波电机模型,第一个模型将采用基波和谐波作为混合激励,而第二个模型将采用单独谐波作为激励。上述2个模型所产生的转子损耗差值,即为谐波引起的实心转子谐波涡流损耗。该模型能够精确考虑不同负载情况下转子表面磁导率分布所引起的谐波透入深度的变化,所计算的谐波涡流损耗精度更高。
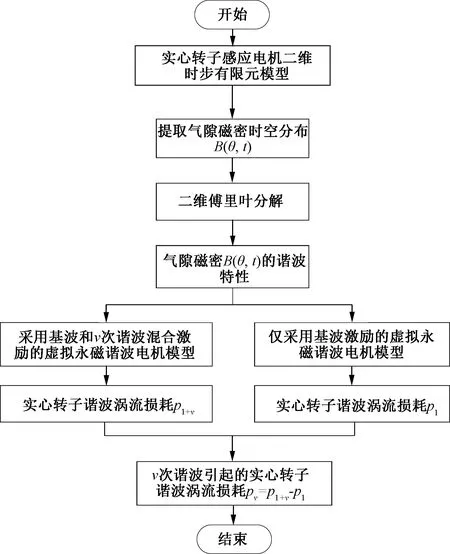
图4 采用混合激励的虚拟永磁谐波电机模型提取转子谐波涡流损耗流程图
然而,上述模型存在的主要问题如下:
(1)求解转子谐波涡流损耗时需要构建2个虚拟永磁谐波电机模型,消耗计算资源较多;
(2)虚拟永磁同步电机模型电磁时间常数较长,收敛时间较慢,增加了损耗提取的时间成本。
综上所述,采用混合激励的虚拟永磁同步电机模型能够有效精确地提取气隙谐波磁场在转子表面引起的谐波涡流损耗,然而其具有消耗计算资源多、计算时间长的缺点。
2.3 采用冻结磁导率的虚拟永磁谐波电机模型
图5显示了采用冻结磁导率的虚拟永磁谐波电机模型构建流程。从图5中可以看出,与采用混合激励的虚拟永磁谐波电机模型相比,采用冻结磁导率的虚拟永磁谐波电机模型只需要构建一个谐波分离模型,并且转子表面磁导率为常数,能够加快非线性求解过程中的迭代计算。此外,采用冻结的常数磁导率后,在保证计算精度的基础上,能够考虑不同负载下的谐波涡流损耗的透入深度,并能够进一步减少转子回路电磁时间常数,缩短模型收敛达到稳态的时间。
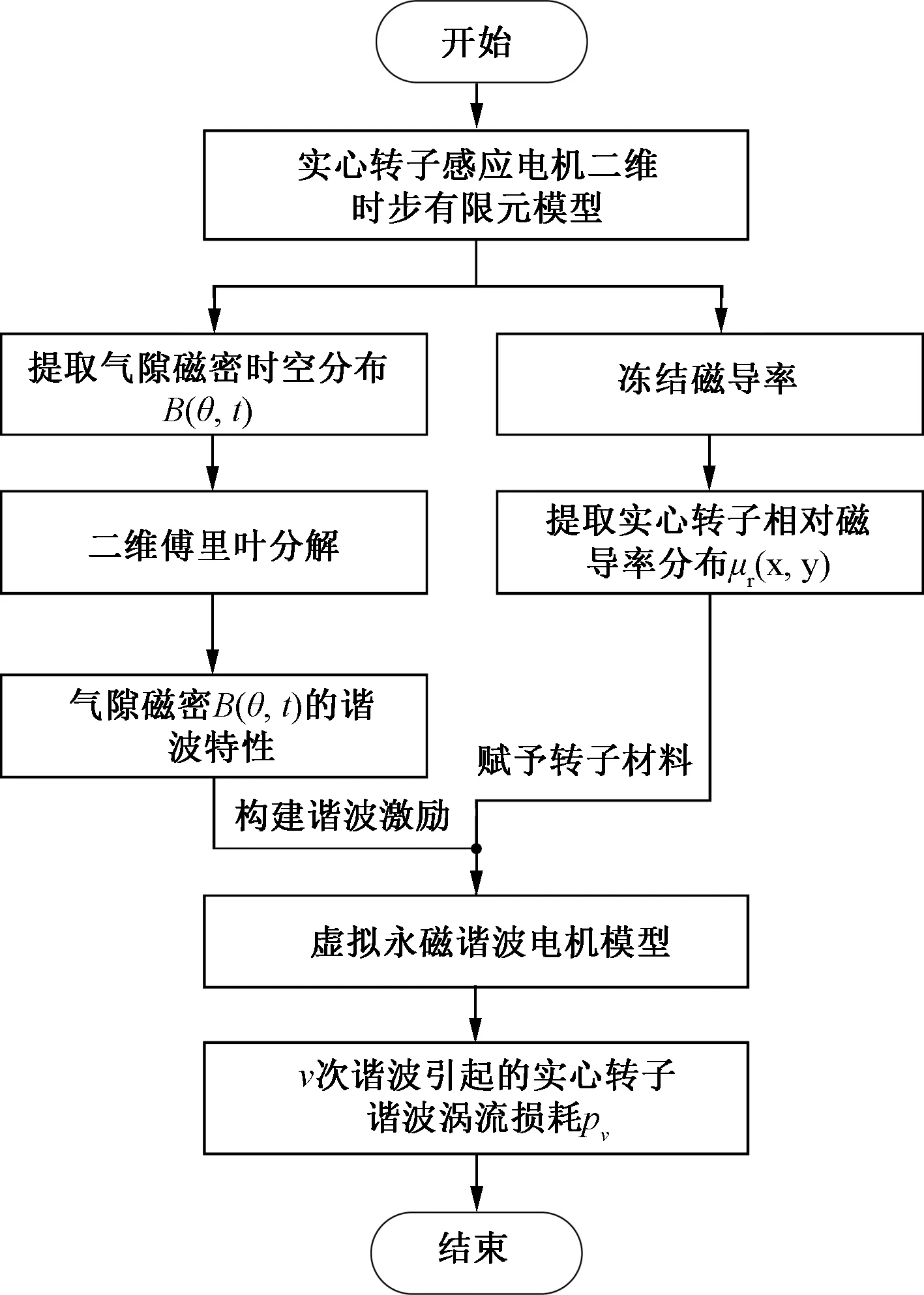
图5 采用冻结磁导率的虚拟永磁谐波电机模型提取转子谐波涡流损耗流程图
3 谐波涡流损耗的分离结果计算对比
图6显示了采用2种虚拟永磁谐波电机模型分离的转子谐波涡流损耗对比图。从图6中可以看出,2种方法计算的涡流损耗误差较小,其中-11次气隙磁场谐波引起的转子谐波涡流损耗较为明显,但谐波幅值仅为0.007 7 T,其损耗较高的原因是谐波阶次较低,在转子表面透入深度较深。此外,-35次气隙磁场谐波引起的谐波涡流损耗最大,原因是其谐波幅值较高,为0.026 T。
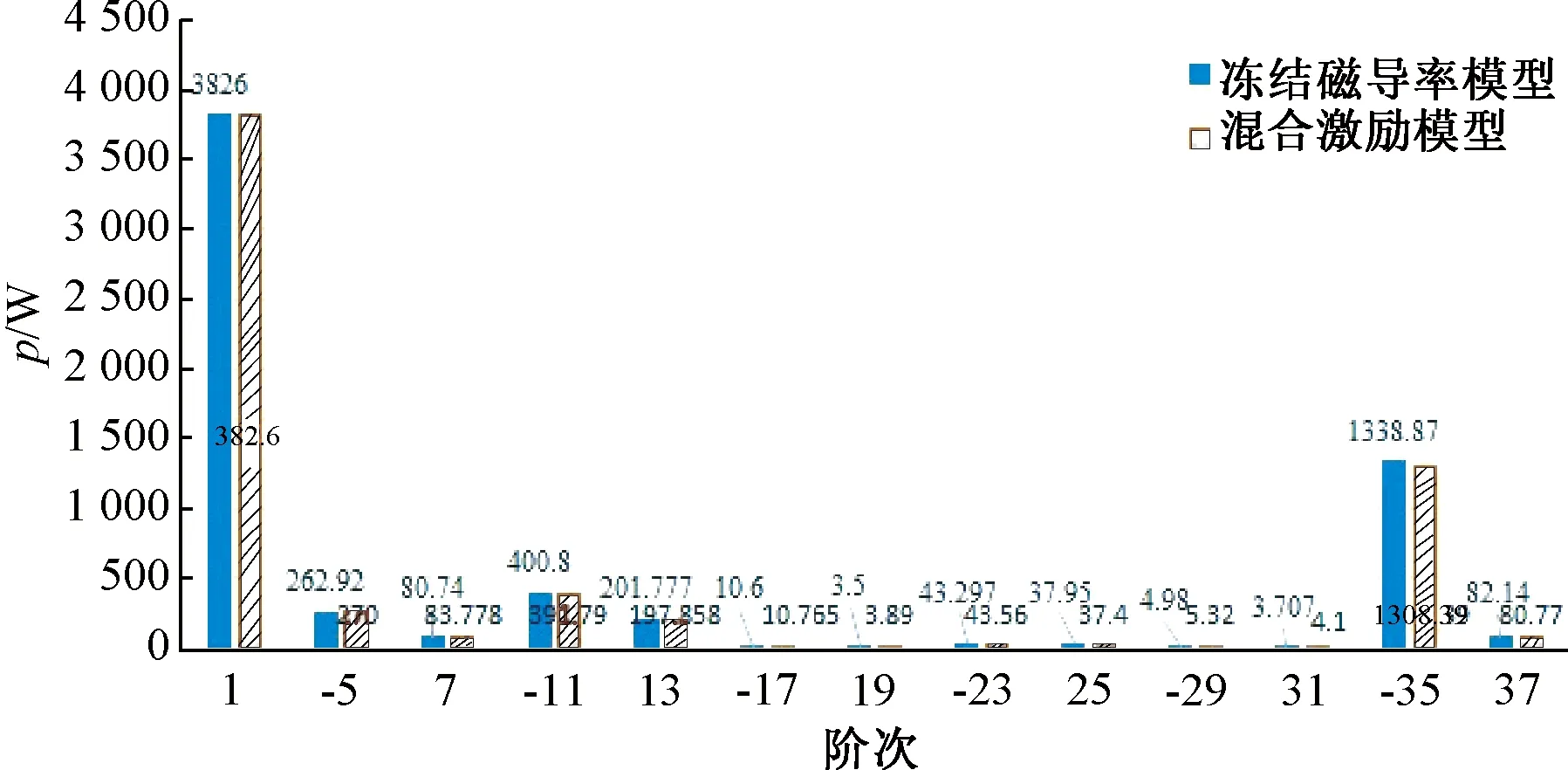
图6 采用虚拟永磁谐波电机模型分离的转子谐波涡流损耗
对图6中采用冻结磁导率模型和混合激励模型计算的转子谐波涡流损耗求和,可以得到总的转子涡流损耗分别为6 297.28 W和6 263.62 W,相对于表2中传统有限元计算方法求得的转子涡流损耗6 559.67 W,相对误差为-4%和-4.5%,该误差可以间接证明虚拟永磁谐波电机模型分离转子谐波涡流损耗具有较高的精度。
图7显示了采用虚拟永磁谐波电机模型分离的-5次谐波在转子表面引起的感应涡流分布。结合表4和图6可以发现,由于谐波感应涡流频率较高,故在转子侧的感应涡流主要集中在转子表面,且透入深度在不同位置处的表现各不相同。由此可知,虚拟永磁谐波电机模型不仅能高精度分离并提取气隙磁场谐波涡流损耗,还能获得损耗分布,能够为后续采取针对性抑制措施提供理论依据。

图7 采用虚拟永磁谐波电机模型分离的-5次谐波在转子表面引起的感应涡流分布
表5列举对比了混合激励和冻结磁导率2种虚拟永磁谐波电机模型的计算时长。计算平台为Intel(R) Core(TM) i9-10940X CPU @ 3.30 GHz,64 GB RAM,1 TB SSD。其中,混合激励虚拟永磁谐波电机模型每次计算需要涵盖2个有限元模型,每个模型仿真计算达到收敛需要10 000步,共计20 000步,耗时约16.67 h;采用冻结磁导率的虚拟永磁谐波电机模型由于实心转子磁导率为常数,能够在仿真计算1 200步以内快速收敛达到稳态,耗时1.2 h。

表5 混合激励和冻结磁导率2种虚拟永磁谐波电机模型的计算时长
4 结 语
本文针对高速实心转子感应电机转子谐波涡流损耗的分离和提取问题,以一台380 V,1 MW,12 000 r/min高速实心转子感应电机为主要研究对象,结合虚拟永磁同步电机模型,采用混合激励和冻结磁导率两种方法,定量分离并提取了气隙谐波磁场在实心转子表面所引起的谐波涡流损耗。分离的转子谐波涡流损耗数据表明,低阶次的绕组相带谐波和定子齿谐波能够在实心转子表面引起较高的高频涡流损耗,其原因为低阶次绕组相带谐波在转子表面所感应的谐波涡流损耗透入深度较深,定子齿谐波幅值较大。
本文提出的高速实心转子感应电机转子谐波涡流损耗的分离方法,不仅能为后续对转子谐波涡流损耗进行有效抑制提供理论基础,还能为分离电机其他谐波电磁性能提供思路。