基于EN 14363:2016(E)的地铁车辆扭曲安全性研究

郭振通 周鲁宁 薛 萍

(南京中车浦镇城轨车辆责任有限公司，210031，南京∥第一作者，高级工程师)

随着我国“一带一路”战略的实施，促进了我国与世界其他各国之间的联系，也为我国的轨道交通走出去提供了良好的契机。然而，各国不同的车辆设计标准是车辆出口面临的重要问题。国外认可的标准主要有EN(欧洲标准)、UIC(国际铁路联盟)和ISO(国际标准化组织)等标准体系。其中，一部分标准是国内的参考标准，例如与车辆运行安全性相关的UIC 518：2009(E)[1-3]，与乘坐舒适性相关的EN 12299：2009(E)和ISO 2631-4：2001(E)[4-5]；但还有一些是国内涉及较少的标准，如EN 14363：2016(E)中提出的车辆在准静态下的车辆脱轨安全性评估。此标准用于评价被试车辆在扭曲状态下的安全性指标。

扭曲状态下的车辆运行安全性指标是车辆静态试验验收中的重要指标，因此对车辆静态性能的研究和动力学模型的验证具有现实意义。本文介绍了两种实验室内模拟车体和转向架扭曲状态的试验方法(无扭曲试验台和有扭曲试验台)，基于地铁车辆的扭曲试验台建立仿真模型，分析了某出口地铁车辆的轮重减载行为，并评估了该车辆的行驶安全性。本研究可为地铁车辆的设计、研发及静态验收提供一定的技术支撑。

1 无扭曲试验台的扭曲试验

在实验室条件下，由于没有扭曲试验台，不能将车轮降低到轨面以下，需要将静止的车轮提升为等效的几何体系。一般而言，车辆处于的最不利状态为车辆的一侧车轮处于水平位置，而另一侧车轮处于倾斜位置，会导致车辆以最大扭曲状态出现。车轮抬升量示意图如图1所示。

根据EN 14363：2016(E)，转向架扭曲量gb1和车体扭曲量gc1分别可以表示为：

gb1=7‰， 2ab<4 m

(1)

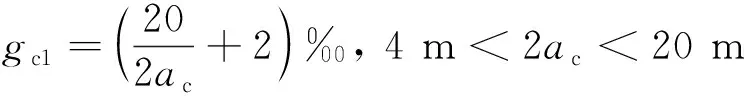
(2)

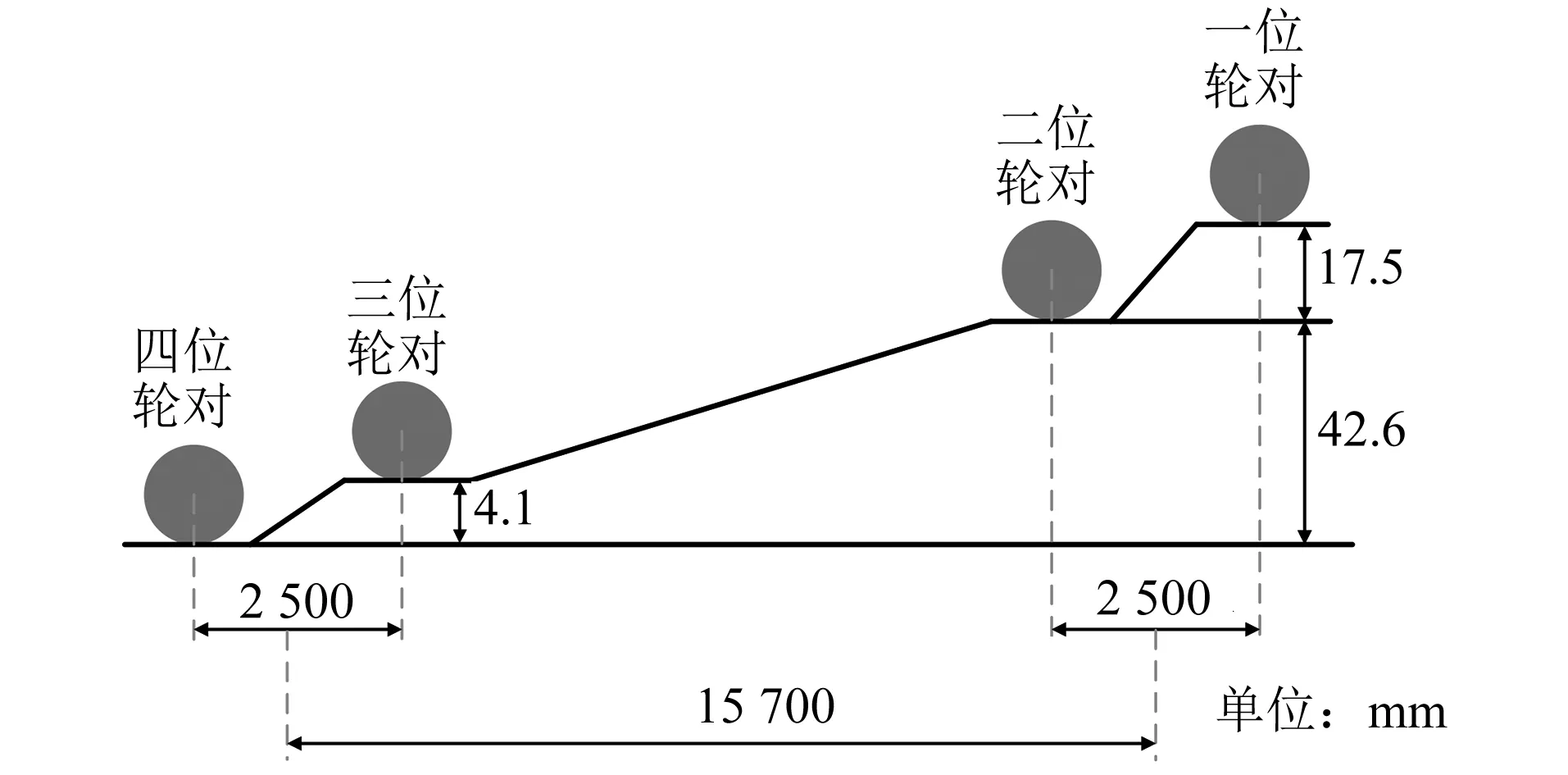
图1 车轮抬升量示意图Fig.1 Diagram of wheel vertical rise amount

式中：

2ab——测试车辆的转向架轴距，m；

2ac——测试车辆的车辆定距，m。

本文测试车辆的车辆定距为12.6 m，转向架轴距为2.5 m。根据式(1)和式(2)可知，转向架扭曲量为7.00‰，车体扭曲量为3.27‰。则一位轮对、二位轮对、三位轮对和四位轮对的车轮抬升量z1—z4依次可以表示为：

根据车轮抬升量可以测试车轮载重的变化，并计算车辆的轮重减载率指标，进而用于车辆在扭曲状态下的安全性评估。

2 有扭曲试验台的扭曲试验

2.1 扭曲量计算方法

EN 14363：2016(E)中着重介绍了通过扭曲试验台的台架试验代替车辆在扭曲轨道上的线路试验。针对车辆在扭曲试验台上的扭曲试验，主要测试车辆的轮重减载情况，评估指标为轮重减载率。以EN 14363：2016(E)中规定的方法二为例，测试车辆的转向架扭曲量gb2和车体扭曲量gc2分别为：

(3)

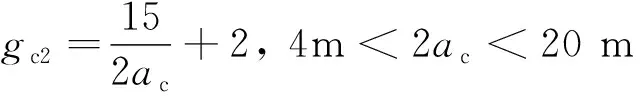
(4)

将测试车辆的车辆定距和转向架轴距分别代入式(3)和式(4)，可以计算获得车体和转向架的扭曲量分别为2.96‰和5.00‰。

2.2 扭曲试验台建模

根据扭曲试验台特征建立扭曲试验台的动力学仿真模型。建立车辆系统动力学模型，车辆采用两级悬挂，一系悬挂采用钢弹簧和轴箱转臂装置，二系悬挂采用空气弹簧[6]。在建模过程中，将车体、构架和轮对等部件考虑为刚体，车体和构架具有6个自由度，轮对具有4个自由度，每个轴箱具有1个点头自由度，整个车辆模型具有42个自由度，车辆部分参数及其取值如表1所示。

表1 车辆部分参数及其取值Tab.1 Some parameters and their values of vehicle

在此基础上，建立载荷施加装置模型，由于要在垂直方向上对车轮施加载荷，所以需要一个中间过渡单元。首先，在大地坐标系下建立基于位移载荷变化规律的各载荷曲线对应的作用体A，作用体A在横向坐标上与车轴中心相同，每条轮对下均建立一个作用体A。然后，建立具有横向和垂向自由度的作动器单元，将作用体A与作用器单元铰接，使得作动器具有载荷属性，进而实现载荷的加载。扭曲试验台动力学仿真模型如图2所示，其中仅标出了四位轮对的作用体A。

图2 扭曲试验台动力学仿真模型Fig.2 Dynamics simulation model of twist test rig

2.3 扭曲量的载荷施加

根据被试车辆是进行车体扭曲试验还是转向架扭曲试验，扭曲试验台对每个车轮的扭曲量载荷施加方法不同。考虑单独车体扭曲的扭曲试验台加载方法参考EN 14363：2016(E)，则其实际扭曲量gc3可以表示为：

(5)

其中：Δz21=Δz11;Δz12=-Δz11;Δz22=-Δz11

式中：

Δzij——车轮抬升量；

i——轮对编号，i=1,2,3,4；

j——轮对的左、右侧车轮，1表示轮对右侧车轮，2表示轮对左侧车轮。

同理，单独转向架扭曲的扭曲试验台加载方法参照EN 14363：2016(E)，则其实际扭曲量gb3可以表示为：

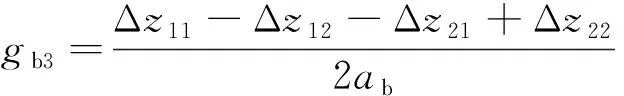
(6)

此外，EN 14363：2016(E)中还规定了车体扭曲和转向架扭曲同时试验的方法。在扭曲试验台上加载如图3所示的位移载荷变化曲线。其中，一位轮对和二位轮对左右两侧位移载荷的施加方向是相反的，即左右两侧的位移载荷大小相同、方向相反。

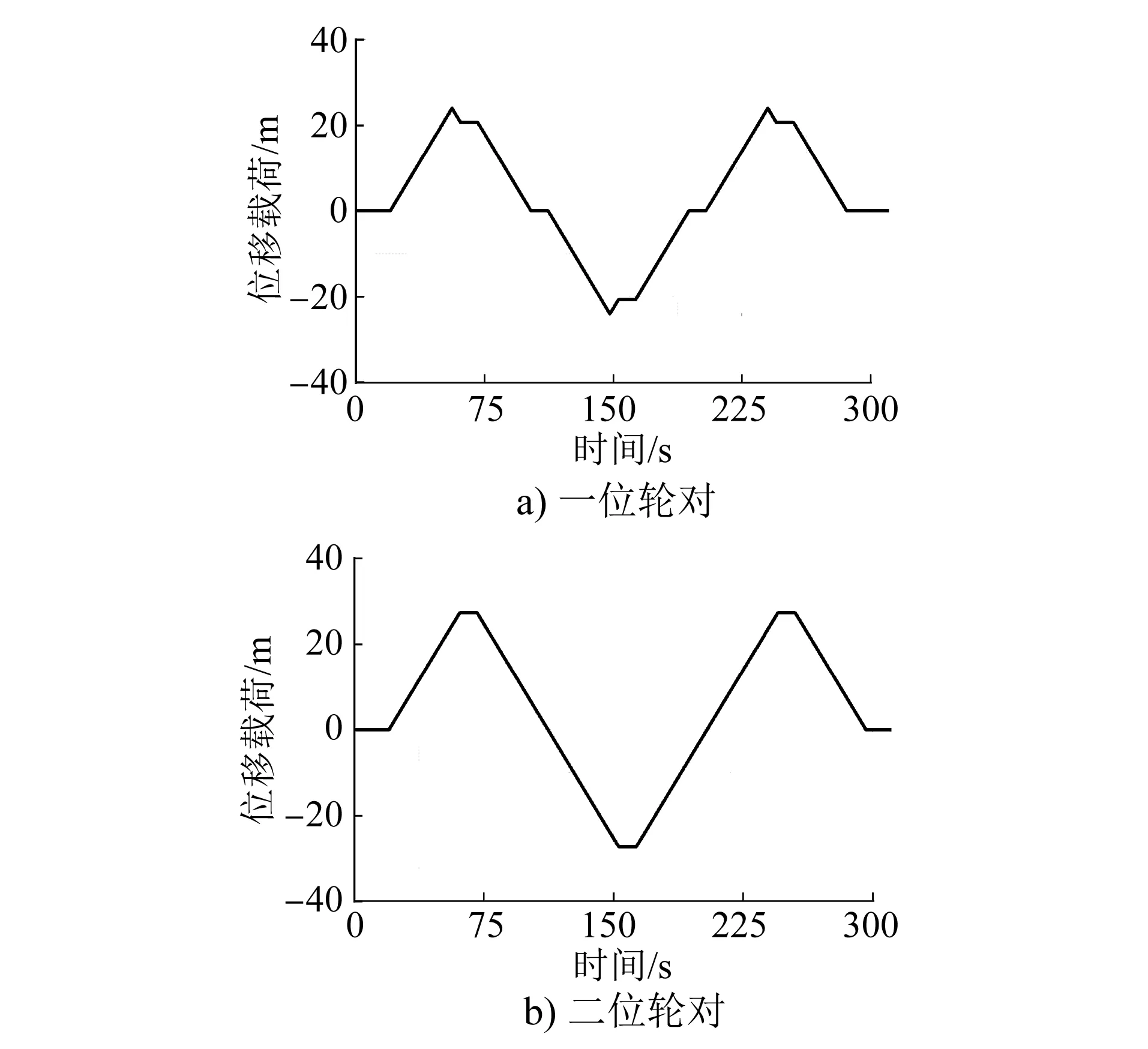
图3 扭曲试验台位移载荷变化曲线Fig.3 Change curve of displacement load on twist test rig

3 仿真分析

利用所建立的扭曲试验台模型在试验台上施加位移载荷变化曲线，仿真并分析车辆在空气弹簧有气和空气弹簧失气两种状态下的轮重减载情况，判断车辆的轮重减载率是否满足标准限值要求。

3.1 空气弹簧有气状态

在扭曲试验台上，被试车辆在空气弹簧有气状态下的前后转向架轮轨垂向力变化趋势如图4所示。由图4可知：在扭曲位移载荷作用下，车轮垂向力存在明显的增载和减载交替变化趋势，且左右两侧车轮的垂向力交替方向是相反的，这与加载的位移载荷方向一致；对于前转向架而言，一位轮对和二位轮对施加的位移载荷变化趋势不同，车轮垂向力变化趋势存在明显差异；对于后转向架而言，由于没有加载位移载荷，三位轮对和四位轮对的轮轨垂向力变化规律类似，差异较小；一位轮对的轮轨垂向力最大值和最小值分别位69.64 kN和25.53 kN。在空气弹簧有气状态下，前转向架一系悬挂的垂向位移变化趋势如图5所示。由图5可知，一系悬挂的垂向位移变化趋势与轮轨垂向力的变化趋势相同，一位轮对左侧和右侧有最大的垂向位移变化量。

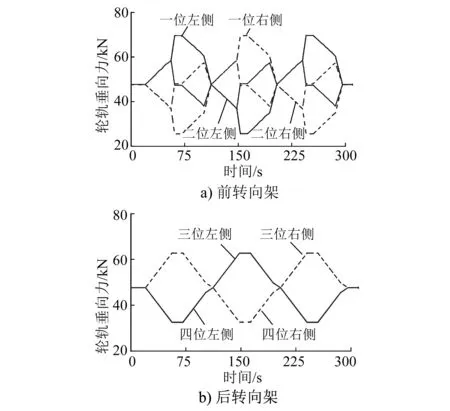
图4 空气弹簧有气状态下前后转向架的轮轨垂向力变化趋势

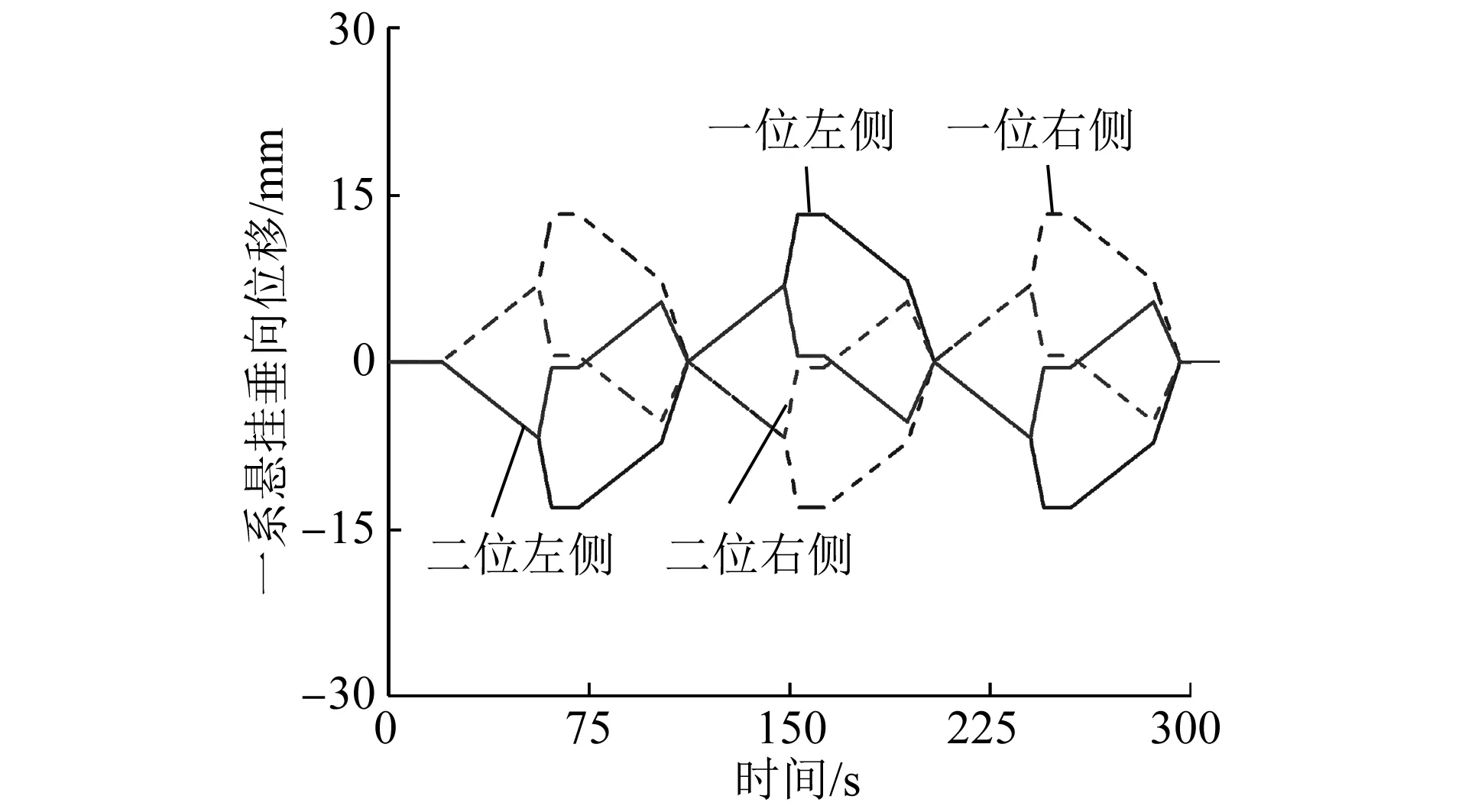
图5 空气弹簧有气状态下前转向架一系悬挂的垂向位移变化趋势

在扭曲载荷下，根据图4中的轮轨垂向力变化趋势可以分析获得相应的轮重减载率，如表2所示。由表2可知，整辆车的轮轨垂向力最小值出现在一位轮对，其大小为25.53 kN，相应的最大轮重减载率为0.46，小于标准规定限值0.60，满足标准要求。由于轮对左右两侧施加的位移载荷大小相同，所以左右两侧车轮的轮重减载率大小基本一致。

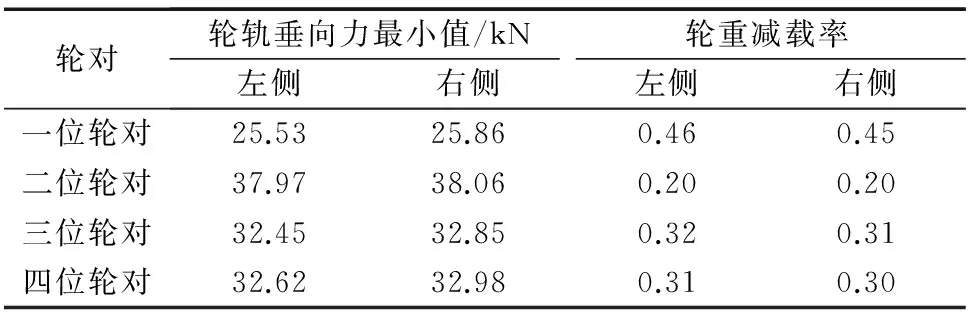
表2 空气弹簧有气状态下的轮重减载率Tab.2 Wheel weight unloading ratio with air spring inflated

3.2 空气弹簧失气状态

在空气弹簧失气状态下，空气弹簧刚度由应急簧刚度提供，二系悬挂垂向刚度明显增大，势必会对扭曲状态下的车辆运行安全性产生明显的影响。因此有必要分析空气弹簧失气状态下，车辆在扭曲试验台上的轮重减载性能。

图6 空气弹簧失气状态下前后转向架的轮轨垂向力变化趋势Fig.6 Wheel/rail vertical force change tendency of front and rear bogies with air spring deflated

空气弹簧失气状态下，前后转向架的轮轨垂向力变化趋势如图6所示。由图6可知：空气弹簧失气状态下的轮轨垂向力变化趋势与空气弹簧有气状态下的轮轨垂向力变化趋势类似，均与扭曲试验台施加的位移载荷相关，与转向架的悬挂参数无关；在空气弹簧无气状态下，轮轨垂向力的增载量和减载量明显大于空气弹簧有气状态下的分析结果，轮轨垂向力最大值和最小值分别为75.57 kN和19.65 kN，说明二系悬挂参数对车辆的抗扭曲性能影响明显。空气弹簧失气状态下，前转向架一系悬挂的垂向位移变化趋势如图7所示。由图5和图7可知，空气弹簧失气和有气状态下的垂向位移变化趋势相同，但其幅值上存在一定差异，空气弹簧失气状态下的一系悬挂垂向位移变化量更大，说明车辆存在更大的增减载状态，与轮轨垂向力的分析结果一致。

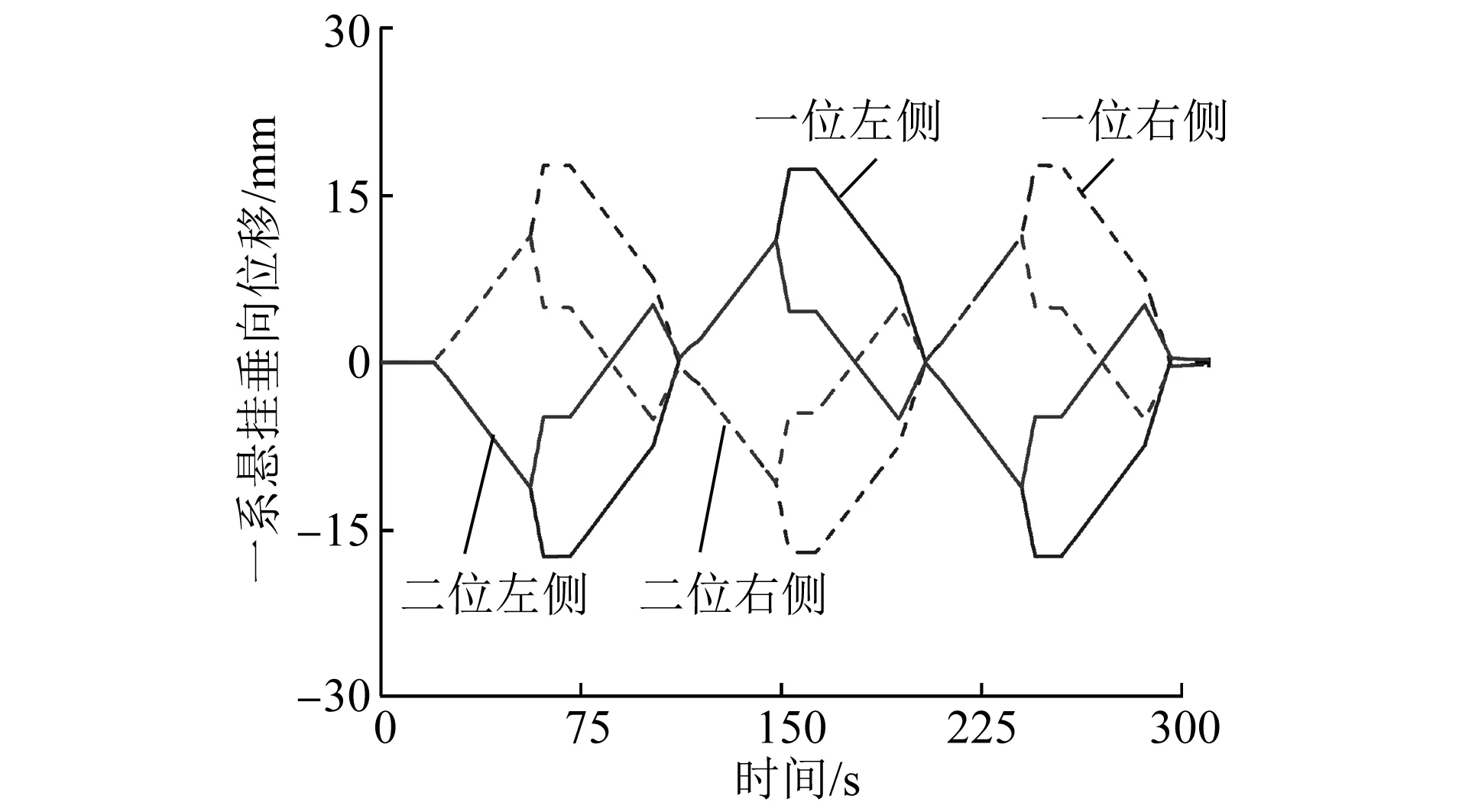
图7 空气弹簧失气状态下前转向架一系悬挂的垂向位移变化趋势

空气弹簧失气状态下的轮重减载率如表3所示。由表3可知，整辆车的车轮轮轨垂向力最小值出现在一位轮对，其大小为19.65 kN，相应的最大轮重减载率为0.59，小于标准规定限值0.60，满足标准要求。由表2和表3可知，空气弹簧失气状态下的车轮轮重减载率均大于空气弹簧有气状态下的值。

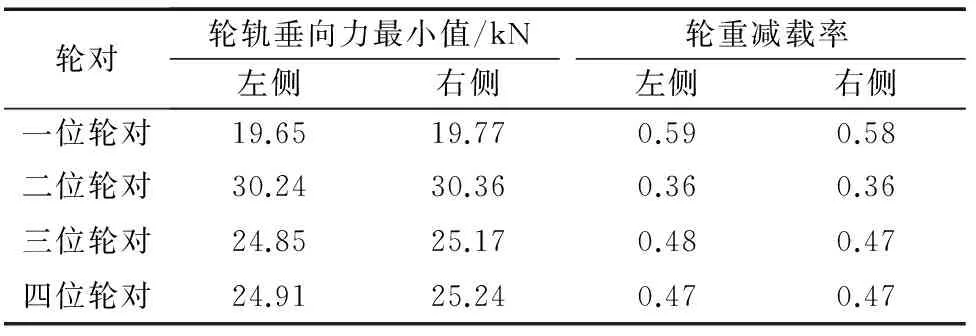
表3 空气弹簧失气状态下的轮重减载率Tab.3 Wheel weight unloading ratio with air spring deflated

4 结语

基于EN 14363：2016(E)的扭曲安全性试验在国内车辆验收中涉及较少的情况，本文首先基于EN 14363：2016(E)详细阐述了实验室内有无扭曲试验台情况下的两种扭曲试验方法，建立了扭曲试验台仿真模型，并分析了在空气弹簧有气和无气状态下的车辆轮重减载情况。计算结果表明，两种状态下的车辆轮重减载率均满足标准要求，且二者在数值上存在明显差异，说明空气弹簧刚度对车辆的抗扭曲安全性有明显的影响。