球状风化体混合花岗岩边坡稳定性分析
李 勇,陈玮龙,许方党,周春梅
(武汉工程大学土木工程与建筑学院,湖北 武汉 430070)
花岗岩中普遍发育着球状风化体(风化孤石),球状风化体的形成受原生节理及风化作用的控制,常呈椭球状或不规则球状。粒径大小不一的风化球体易受外界因素的扰动,形成高空落石或坡面滚石,坚硬的风化球体与残积土或全风化岩混杂的斜坡受降雨或开挖的影响易产生崩塌和滑坡,形成复杂的斜坡地质灾害[1]。
花岗岩球状风化体具有分布不确定性、埋藏边界的隐蔽性等特点,目前学者们对含块石的边坡稳定性进行了一系列研究。如:张森等[2]提出了运用离散元数值模型随机生成技术(PFC2D)生成土石混合体边坡数值模型,并运用强度折减法(ABAQUS)开展了块石含量对边坡稳定性影响的数值分析;刘顺青等[3]利用MATLAB随机生成了含石率从10%~60%的土石混合体边坡数值模型,每种含石率均考虑8种不同的块石分布位置,并采用有限元极限分析法对土石混合体边坡稳定性进行了数值分析;刘晓华等[4]利用MATLAB建立了球状风化体花岗岩边坡数值模型,采用DISTMESH2D对模型进行网格划分,并基于FLAC3D对边坡稳定性进行了分析;钟宇等[5]利用自主研制的电火花震源等探测系统和地质专家分析法,揭示了探测区域球状风化体的空间分布规律;严颖等[6]利用离散元软件,研究了块石含量和空间分布对土石混合体抗剪强度的影响;李建强等[7]采用地表调绘、钻探、物探三种手段, 从不同角度对花岗岩球状风化的地表分布特征和地下分布特征进行了研究, 并进行了综合对比分析;林镇等[8]利用工程地质分析与数值模拟相结合的方法,研究了球状风化体花岗岩边坡滚石的运动轨迹、停滞概率和冲击特性等成灾规律,并模拟分析了坡形坡率优化、平台缓冲介质和滚石拦挡措施的减灾机理和工程效果;黄恒儒[9]对花岗岩球状风化体的形成机制以及盾构穿越球状风化体群产生的地面沉降、姿态控制、设备安全的风险进行了研究;董荣[10]研究了花岗岩球状风化体的形成机理,认为花岗岩球状风化是亲水矿物吸水及失水造成的膨胀收缩的结果;李新峰等[11]通过对云南临沧特殊风化花岗岩建坝实践和资料进行分析,提出了坝基设计所需的关键地质参数;黄献文等[12]利用MIDAS GTS分析得出不同的较大块石分布位置对土石混合体边坡稳定性的影响较大;Cao等[13]研究了基于干湿循环条件下盐浓度对花岗岩风化程度的影响;Qi等[14]通过物理模型试验,研究了降雨入渗条件下全风化花岗岩边坡的响应规律;李凯等[15]通过物理力学试验,研究了饱和度对湿热地区风化花岗岩双层土质边坡抗剪强度的影响;卢有谦等[16]以不同风化程度的花岗岩双层土质边坡土体为研究对象,利用压力板法和饱和盐溶液蒸汽平衡法,研究了在全吸力范围内压实样的持水特性;李杰林等[17]通过冻融循环试验,研究了风化岩石在冻融循环作用下物理特性的变化规律。
综上所述,目前有关花岗岩球状风化体的研究进展较快,但针对球状风化体的存在对混合花岗岩边坡稳定性的影响未做系统的研究。为此,本文依托云南省墨江至临沧公路SJ-4土建20标段拟修建的工程实例,针对球状风化体对混合花岗岩边坡稳定性的影响做详细研究。首先通过MATLAB平台建立随机场,并将MATLAB数据导入到CAD,再导入到GeoStudio数值模拟软件,以此来建模;然后通过调整土体参数来模拟球状风化体混合花岗岩边坡,从而进行边坡稳定性分析,并研究球状风化体的含量、直径和位置对混合花岗岩边坡稳定性的影响,以为球状风化体混合花岗岩边坡设计与施工提供参考依据。
1 工程背景
拟修建公路工程位于云南省墨江至临沧公路SJ-4土建20标段,拟建路线右K248+495~右K248+800.86段地形起伏较大,设计拟以深挖路堑形式通过。该深挖路段总长为305.86 m,中心最大挖方高度约21.16 m,该深挖路堑段施工开挖后,将在右侧形成高约62.31 m的岩土质边坡,该边坡坡比按1∶0.75~1∶1.00选用,8~10 m分台,平台宽2 m。该边坡岩土体岩性为粉质黏土及全风化花岗岩,全风化花岗岩呈砂土状散体结构,遇水易崩解,加之球状风化体的存在易形成落石及崩塌,边坡稳定性较差,属不稳定结构。该边坡开挖横断面和纵剖面示意图如图1和图2所示。

图1 K248+640标段球状风化体混合花岗岩边坡横 断面示意图

图2 K248+640标段球状风化体混合花岗岩边坡纵 剖面示意图
根据云南省墨江至临沧公路地质调查、钻孔揭露和瞬变电磁法测试结果可知,挖方路堑段水文地质条件较简单,地下水水位埋深较深,对挖方路堑段的影响较小,因此在本次深挖段边坡稳定性计算分析中,未考虑地下水对边坡稳定性的影响。
根据勘察和物探测试结果以及边坡开挖后揭露情况,本文在边坡稳定性分析中,考虑全风化花岗岩中裹有直径约2 m左右的球状风化体(称之为混合花岗岩),球状风化体面积占斜坡截面积的5%~40%(按5%、10%、15%、20%、25%、30%、35%和40%分别计算,视作球状风化体含量),埋置深度随机分布。
2 球状风化体混合花岗岩边坡数值模型构建
2. 1 随机场理论引入数值模型
花岗岩中普遍发育球状风化体(即风化孤石),孤石分布具有不均匀、离散性强的特点,因此引入随机场理论模拟孤石的实际分布情况。特殊区域的孤石分布规律具有相似性,因此该结论可为具有相似条件的地区提供参考。对于目标段K248,要考虑风化层中裹有直径约为2 m左右的球状风化体,基于MATLAB平台,用直径为2 m的圆来近似模拟球状风化体。对于此边坡,取其深挖工程地质断面图进行二维分析。简化边坡面为一条直线,坡高为78.0 m,靠近公路边坡高为15.8 m,长为62.3 m,坡度近似为45°,以这个梯形近似模拟该拟建公路项目的边坡。利用MATLAB平台在此梯形内设立随机圆,圆的面积分别占梯形总面积的5%、10%、15%、20%、25%、30%、35%和40%(即球状风化体含量),以此来模拟球状风化体在边坡体中的随机分布。基于MATLAB平台作出的球状风化体随机分布图(以球状风化体含量10%为例),见图3。
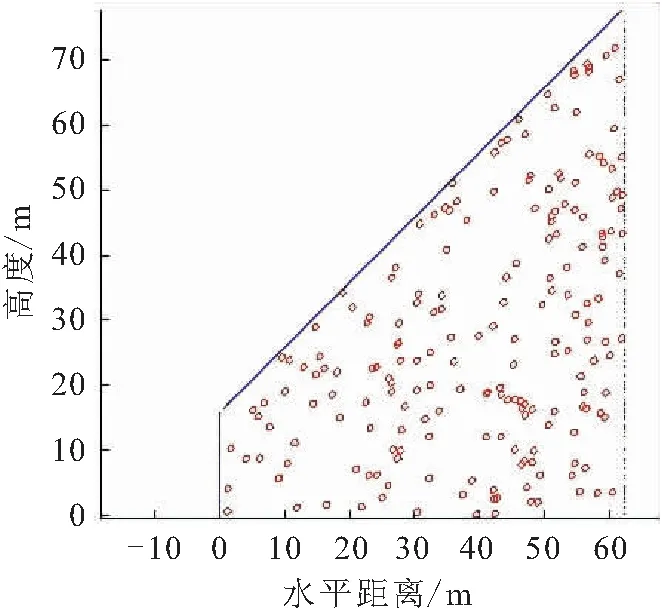
图3 球状风化体随机分布图(球状风化体含量为10%)
本文将针对花岗岩球状风化这一特殊的边坡稳定性问题,先利用随机场理论,基于MATLAB平台,生成球状风化体在混合花岗岩边坡内的随机分布场;然后将MATLAB数据导入到CAD,再导入到GeoStudio数值模拟软件,以此来建模;最后通过调整土体参数来模拟混合花岗岩边坡,从而进行边坡稳定性分析。
2. 2 球状风化体混合花岗岩边坡数值模型构建
根据当地滑坡数据并结合文献[11]可知,该地区滑动面深度平均在20~30 m之间,因此结合已获取的球状风化体分布随机场模型,本文构建了两个不同的球状风化体混合花岗岩边坡数值模型:球状风化体仅分布在最危险滑动面以上的混合花岗岩边坡数值模型[见图4(a)];在此基础上最危险滑动面以下随机分布球状风化体的混合花岗岩边坡数值模型[见图4(b)]。构建这两个边坡数值模型的目的是研究球状风化体对混合花岗岩边坡稳定性的影响,以及球状风化体的分布对混合花岗岩边坡稳定性的影响。

图4 球状风化体混合花岗岩边坡数值模型
根据勘察报告给出的材料参数,并结合试验及现场勘探,获得用于数值计算的球状风化体混合花岗岩边坡岩土体的物理力学性质参数,如表1所示。
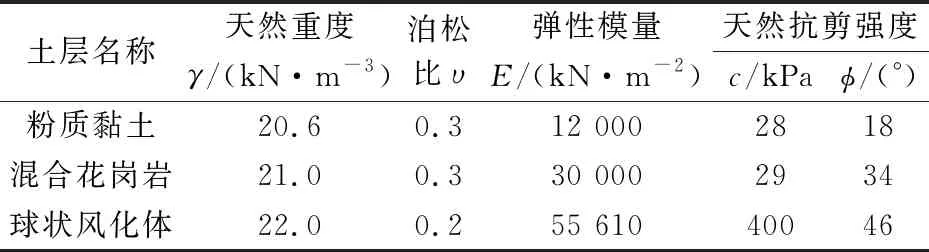
表1 球状风化体混合花岗岩边坡岩土体物理力学性质参数
通过以上两个不同的球状风化体混合花岗岩边坡数值模型得到的边坡位移图,如图5所示。

图5 球状风化体混合花岗岩边坡位移图
由图5可以看出:当有球状风化体分布在混合花岗岩边坡中时,边坡的位移曲线并不是圆弧状,而是会绕开球状风化体,呈现出明显的绕石效应;当滑动面发生在边坡的中下缘,且当整体球状风化体含量提高时,滑动面位置会因为重力作用向边坡下部偏移;当球状风化体含量继续提高时,球状风化体会逐渐取代土体的骨架作用,趋向于岩质边坡,因此边坡的最大位移变小。
通过数值计算后两个不同混合花岗岩边坡的稳定性系数如下:仅最危险滑动面以上分布球状风化体混合花岗岩边坡的稳定性系数为1.17;随机分布球状风化体混合花岗岩边坡的稳定性系数为1.17。通过对比发现,当最危险滑动面以下增加球状风化体时,对混合花岗岩边坡整体稳定性的影响很小。因此在接下来的建模中,将忽略最危险滑动面以下球状风化体对混合花岗岩边坡稳定性的影响,仅考虑最危险滑动面以上球状风化体对混合花岗岩边坡稳定性的影响。
3 球状风化体混合花岗岩边坡稳定性分析
本文选用GeoStudio软件中的SLOPE/W模块(边坡稳定分析模块)和SIGMA/W模块(岩土应力变形分析模块)对球状风化体混合花岗岩边坡稳定性进行分析,并运用经典土力学理论极限平衡法研究边坡稳定性的变化规律。
3. 1 球状风化体含量对混合花岗岩边坡稳定性的影响
在球状风化体混合花岗岩边坡中,球状风化体含量(PR)的多少可能会影响边坡的稳定性。根据上一节的结论,最危险滑动面以下的球状风化体对混合花岗岩边坡稳定性的影响较小,且平均风化深度在30 m以内,因此本文的建模均仅考虑风化层厚度为30 m以内的球状风化体。根据勘察报告可知,该地区球状风化体含量在30%以内,故在建模分析时本文考虑球状风化体含量最高为40%,以探索球状风化体含量对混合花岗岩边坡稳定性的影响规律。本文考虑球状风化体含量PR分别为0%、5%、10%、15%、20%、25%、30%、35%和40%时,通过计算球状风化体混合花岗岩边坡的稳定性系数FS,并搜索最危险滑动面,从而得到不同球状风化体含量下混合花岗岩边坡内部岩土体抗剪强度和稳定性系数及其稳定性变化规律,见图6至图8。

图6 不同球状风化体含量(PR)下混合花岗岩边坡 内部岩土体的抗剪强度
由图6至图8可以看出:随着球状风化体含量的增加,混合花岗岩边坡内部岩土体的抗剪强度和稳定性系数(即安全系数FS)发生了很大的变化,具体分析如下:
(1) 对于该混合花岗岩边坡岩土体的抗剪强度,沿着水平方向均呈抛物线型,即边坡岩土体抗剪强度先增加后减少,随着球状风化体含量的增加,其滑动面处岩土体抗剪强度不断增加,岩土体最大抗剪强度出现在边坡中间60~70 m部位;随着球状风化体含量由0%变化到30%,边坡岩土体最大抗剪强度由180 kPa变化为400 kPa(见图6)。这是因为在球状风化体含量较低时,球状风化体在整个岩土结构中是悬浮状态,其整体结构仍可认为是土质边坡;随着球状风化体含量不断提升,球状风化体在岩土结构中所占比重越来越大,逐渐成为整个边坡的骨架,此时呈现的状态类似于岩质边坡,因此其抗剪强度在不断提高。边坡岩土体抗剪强度的突变现象,是由于在极限平衡法的条分过程中,条块底部,也就是与滑动面接触的部分穿过了球状风化体,而球状风化体的抗剪强度是很高的,类似于岩质结构,因此在图6(b)中会存在边坡岩土体抗剪强度突变现象。该观点与文献[6]观点一致。
(2) 随着球状风化体含量(0%~40%之间)的增加,混合花岗岩边坡的最危险滑动面位置越来越往深部发展,同时边坡的稳定性逐渐增大(见图7)。这是因为随着球状风化体含量的增加,球状风化体构成了混合花岗岩边坡内部的受力骨架,提高了边坡岩土体整体的抗剪强度,边坡的稳定性提高。
(3) 将混合花岗岩边坡稳定性系数(FS)与球状风化体含量(PR)进行分段线性拟合,有:

图7 不同球状风化体含量(PR)下混合花岗岩边坡 的稳定性系数(FS)和最危险滑动面位置

图8 不同球状风化体含量(PR)下混合花岗岩边坡 稳定性的变化规律

(1)
对于该混合花岗岩边坡的稳定性系数FS,当球状风化体含量在5%以内时,边坡稳定性系数基本不变;当球状风化体含量在5%~20%之间时,边坡稳定性系数呈快速增加的趋势;当球状风化体含量超过20%时,边坡稳定性系数呈缓慢增加趋势(见图8)。
3.2 球状风化体直径对混合花岗岩边坡稳定性的影响
由于球状风化体直径(D)大小不同,故本文考虑了球状风化体直径可能对混合花岗岩边坡的稳定性产生影响。结合地勘报告可知,该地区球状风化体直径在2 m左右,因此在控制球状风化体含量一定的情况下(球状风化体含量为滑动面以上土体总面积的15%),本文选取D分别为1.4 m、1.7 m、2.2 m、3.0 m和3.8 m的球状风化体对混合花岗岩边坡稳定性进行了分析研究。建立的边坡稳定性分析模型如图9所示,边坡最危险滑动面位置变化如图10所示,计算出的边坡稳定性系数如表2所示。

图9 不同球状风化体直径(D)下混合花岗岩边坡的稳 定性分析模型
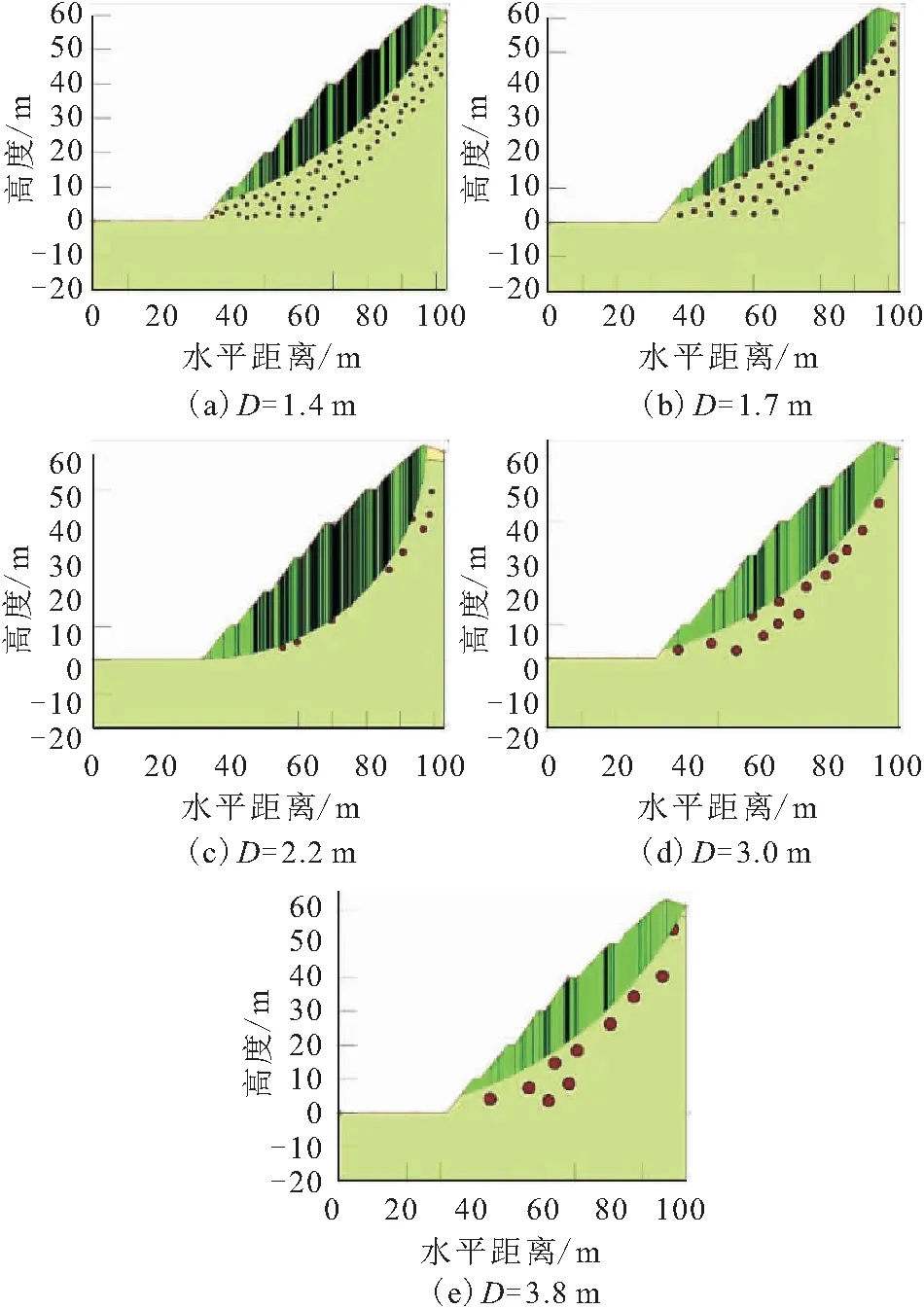
图10 不同球状风化体直径(D)下混合花岗岩边坡的 最危险滑动面位置
由图10可知:当球状风化体直径逐渐变大时,混合花岗岩边坡的滑动面深度是先变深后变浅,这是由于当球状风化体直径较小且球状风化体含量并不高时,整个边坡仍属于土质边坡,因此滑动面仍为土质边坡的滑动面;随着球状风化体直径的增大,存在球状风化体部分的土体与球状风化体有足够的咬合力形成一个整体,整个边坡呈现一部分岩质边坡的特性,因此滑动面深度加大;当球状风化体直径继续增大时,由于其直径过大,这时的球状风化体又成为一个孤立的块体,边坡又以土体为骨架结构,因此滑动面逐渐变小。
由表2可知,当球状风化体直径逐渐变大时,混合花岗岩边坡的稳定性系数逐渐减小。因此,对于大直径球状风化体,可能会对混合花岗岩边坡造成不利的影响,尤其是边坡表层有球状风化体,且存在开挖或降雨因素时,易形成落石及崩塌,属不稳定结构,应加强监测和防范。但需要注意的是,本文在此仅考虑了球状风化体直径的影响,未考虑球状风化体位置的影响,通过计算可知,当大直径球状风化体集中在混合花岗岩边坡下部时,边坡稳定性会有提高,因此有必要对球状风化体位置对混合花岗岩边坡稳定性的影响进行讨论。

表2 不同球状风化体直径(D)下混合花岗岩边坡的稳定性系数(FS)
3.3 球状风化体位置对混合花岗岩边坡稳定性的影响
在控制球状风化体含量和直径一定的情况下,本文分别研究了当球状风化体分布在混合花岗岩边坡上、中、下部以及分布在边坡浅层和深层时边坡的稳定性变化规律。故本文选取直径为2.2 m的球状风化体,建立的边坡稳定性分析模型如图11所示,计算出的边坡稳定性系数如表3所示。

图11 不同球状风化体位置下混合花岗岩边坡的稳 定性分析模型

表3 不同球状风化体位置下混合花岗岩边坡的稳定性系数(FS)
由表3可知:当球状风化体分布在混合花岗岩边坡的上部时边坡的稳定性系数最小,分布在混合花岗岩边坡的中部时边坡的稳定性系数次之,当球状风化体分布在混合花岗岩边坡的下部时边坡的稳定性系数最大。这是由于压脚作用越来越明显,高密度和高强度的球状风化体,使得混合花岗岩边坡的抗滑力显著提升,对于提高边坡稳定性有积极的作用。与此同时,球状风化体分布在混合花岗岩边坡浅层时边坡的稳定性系数比球状风化体分布在混合花岗岩边坡深层时大。由前述可知,位置越深的球状风化体,对混合花岗岩边坡稳定性的影响越小,且球状风化体存在本身对边坡稳定性有积极的影响,因此球状风化体位置越浅的边坡稳定性系数越高。
本文认为球状风化体位置对土石混合体边坡稳定性的影响较大,影响大小关系表现为:边坡下部>边坡中部>边坡上部,边坡浅层>边坡深层。该结论与文献[12]的观点一致。
3. 4 绕石效应分析
在假设边坡为近似圆弧滑动的基础上通过分析可知,当孤石出现在边坡滑动面上时,边坡滑动面明显不会穿过孤石,这是由于孤石抗剪强度过高,如果边坡滑动面穿过孤石,边坡的抗滑力会大幅度提高而边坡下滑力并没有发生明显的变化,故并不会发生滑坡,进而不存在边坡滑动面。因此,需要对于孤石对边坡滑动面的影响进行分析。通过Slope建立分析模型,在无孤石边坡[见图12(a)]的基础上增加孤石,让边坡最危险滑动面穿过孤石,即建立两种模型:一种是孤石位置偏向边坡滑动面上方[见图12(c)];一种是孤石位置偏向边坡滑动面下方[见图12(e)]。建立的绕石效应分析模型以及对应的边坡稳定性系数,见图12。图中黑色的线代表无孤石情况下的边坡滑动面,绿色区域代表加入孤石以后的边坡滑动面。
通过对这两种边坡滑动面进行对比分析可知:边坡滑动面上加入孤石以后,边坡最危险滑动面会随着孤石的加入而发生改变,并呈现明显的绕开孤石的效应,即绕石效应,但其不是仅在孤石附近绕,而是呈现整体式绕开孤石;当孤石位置偏向边坡最危险滑动面上方时,边坡最危险滑动面会从孤石下方绕[见图12(d)];当孤石位置偏向边坡最危险滑动面下方时,边坡最危险滑动面会从孤石上方绕[见图12(f)]。由此可得,当边坡滑动面上出现孤石时,边坡滑动面不会穿过孤石,而是会绕过孤石,而且绕过孤石的方式是选择 “更近”的路径。这是由于当边坡滑动面要发生改变时,必然要消耗能量,因此为了保证消耗的能量最低,必然会选择 “最近”的路径绕过孤石。

图12 绕石效应分析模型及对应的边坡稳定性系数(FS)
4 讨 论
(1) 仅考虑滑动面以上分布球状风化体和整体随机分布球状风化体,混合花岗岩边坡的稳定性系数一致。当在滑动面以下增加球状风化体时,对整体边坡稳定性的影响很小。因此在建模中,本文忽略滑动面以下球状风化体对混合花岗岩边坡稳定性的影响,仅考虑滑动面以上球状风化体对混合花岗岩边坡稳定性的影响。
(2) 当考虑球状风化体随机分布时,相对于实际来说球状风化体仍是分布较均匀的,而实际混合花岗岩边坡中可能存在部分位置球状风化体分布较集中、部分位置较分散的情况,因此建模与实际情况有一定的差异。
(3) 在混合花岗岩边坡稳定性计算中,假设球状风化体是均质、规则且刚度大的球形,而实际的球状风化体并非规则的球形,且可能存在一些微裂纹,这与实际球状风化体有些区别,但这并不影响对混合花岗岩边坡稳定性的分析。
5 结 论
(1) 球状风化体的含量对混合花岗岩边坡稳定性有一定的影响。随着球状风化体含量由0%增加到40%,混合花岗岩边坡的稳定性系数整体呈上升趋势。当球状风化体含量由10%增加至20%时,边坡的稳定性系数增加较快;当球状风化体含量超过20%时,边坡稳定性系数基本不变。随着球状风化体含量的增加,混合花岗岩边坡的最危险滑动面向深部发展。
(2) 球状风化体直径对混合花岗岩边坡稳定性有影响。当球状风化体直径变大时,滑动面深度先变大后变小,混合花岗岩边坡的稳定性系数逐渐变小。当边坡表层有大直径球状风化体时,由于开挖或降雨因素易形成落石及崩塌,属不稳定结构,应加强监测和防范。
(3) 球状风化体位置对混合花岗岩边坡稳定性有一定的影响。当球状风化体分布在混合花岗岩边坡的上部时边坡的稳定性系数最小,分布在混合花岗岩边坡中部时边坡的稳定性系数次之,分布在混合花岗岩边坡下部时边坡的稳定性系数最大;球状风化体分布在混合花岗岩边坡浅层时边坡的稳定性系数比分布在深层时大。球状风化体位置分布对混合花岗岩边坡稳定性具体的影响关系表现为:边坡下部>边坡中部>边坡上部,边坡浅层>边坡深层。
(4) 在无孤石边坡的基础上加入孤石以后,最危险滑动面会随着孤石的加入而发生改变,并呈现明显的绕开孤石的效应,但最危险滑动面不是仅在孤石附近绕,而是呈现整体式绕开孤石。当孤石分布在边坡滑动面偏向上方时,最危险滑动面会从孤石下方绕;当孤石分布在边坡滑动面偏向下方时,最危险滑动面会从孤石上方绕。

