高速磁浮列车近场气动特性及其诱导噪声的数值仿真研究

王世浚,朱雷威,孙玉玺,付善强,张保成,赵 波

(1.中国海洋大学工程学院,山东青岛 266000;2.中车青岛四方机车车辆股份有限公司,山东青岛 266000;3.中山大学海洋工程与技术学院,广东珠海 518000)

随着列车运行速度的不断提高，列车受到气动作用诱导的振动和噪声愈发剧烈，高速列车的噪声控制尤为重要[1-2]，尤其是500 Hz以下的低频噪声，具有不易衰减、传播距离远、通透力强和控制难度高等特点，大大降低了车内旅客的乘坐舒适性[3].伴随着由中国中车研制的时速600公里高速磁浮列车成功下线，对其气动诱导噪声研究具有重要的意义.

高速列车因其轮毂与车轮以及车轮与轨道间的接触，使其产生相应的摩擦磨损、接触疲劳问题与噪声问题[4].相较于传统列车，磁浮列车车身与轨道非接触，其主要噪声来源由轮轨摩擦产生的机械噪声转变为由气动阻力所产生的气动噪声[5-8].当行驶速度超过300 km/h时，列车所受空气阻力占总阻力的80%以上[9-11].气动噪声主要来源于表面空气的湍流运动，涡流的运动引起表面脉动压力，继而引起表面的振动，引发强力的空气动力噪声[12].目前，对高速列车气动噪声的研究主要是通过数值模拟和试验研究.数值模拟方面，研究者们对于列车表面复杂流线型与车身结构的研究多采用简化模型.姜世杰等[13]对高速列车进行了列车模型湍流流场模拟，结合外流场测试结果，完成了列车远场气动噪声的预测.Li等[14]通过采用大涡模拟法和声类比方程，研究了缩比车厢模型的远场噪声，结合试验验证了所用仿真方法的预测精度.考虑到实车试验环境的复杂性，Deng等[15]对三编组1:8缩比车厢进行了风洞试验，分析出其空气动力噪声源的分布情况和频率特性.Wang等[16]采用移动列车风洞试验系统，分析出列车行驶过程中，由侧风所导致的空气动力学特性. Nagakura等[17]采用风洞试验、声阵列技术和Lighthill声学比拟理论，指出高速列车的主要气动噪声源为受电弓、转向架、鼻尖、车辆连接处和裙板等.

目前，虽然国内外对列车气动噪声进行了较多研究工作，但大部分研究主要针对时速在300～400公里之间的情况，对于更高行驶速度下气动噪声的影响，还缺少相关的理论研究.伴随着时速600公里的磁浮列车下线，其噪声问题成为列车能否投入使用的重要影响因素.本文中主要基于计算流体动力学与有限元法，开展更高速磁浮列车涉及近场气动噪声激励源特性分析，揭示气动载荷分布规律及其诱导车内振动噪声响应特性，为列车减振降噪设计提供理论依据和技术支持.

1 高速列车气动噪声计算模型

1.1 气动噪声数值模拟理论

高速列车气动噪声来源于由空气流体自身不规则运动以及流体与壁面间的耦合作用，且声场从本质上属于一种特殊流场[18]，因此本文中运用Lighthill波动方程进行气动噪声模拟.方程基于Navier-Stokes(NS)方程和连续性方程，通过将流场和声波动方程进行类比，并将相异的部分视为声源.该方程可表述为[19]

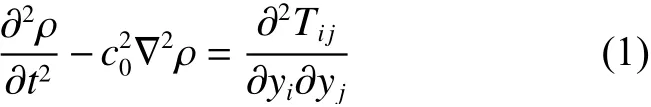
式中，Tij=ρuiuj+pδij+τij−c20ρδij，Tij为Lighthill张量.ui j、p、t、yij和 ρ分别为流体速度、压力、时间、方向和密度，c0为声速， δij为 Kronecker符号， τi j为流体黏性力张量.

考虑到运动固体边界对声学的影响，Ffowcs Williams和Hawkings在基于Lighthill声学方程，进一步推导了FW-H声学类比方程[20]，并表述为

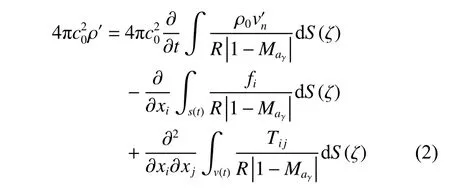
式 中， ρ0为 流 体 原 密 度， ρ′为 流 体 密 度 的 波 动 值，ρ′=ρ−ρ0；S(t)为 运动固体的表面，v(t)为固体的运动速度，v′n为运动固体在其表面单位法向方向n的相对速度；R=|x+y|，x为 接受点位置，xi和xj分别表示该位置的直角坐标分量，y为声源点位置；Maγ为马赫数在观测方向上的投影，S(ζ)为 积分表面，Tij为Lighthill张量；fi为 静止固体边界的单位法向量；c0为声速.

目前，考虑到在复杂雷诺数湍流流动中，直接求解Navier-Stokes方程的方法不易实现，为了兼顾求解效率和求解精度，本文中采用大涡模拟法(LES)[21].大涡模拟是计算流体动力学领域采用的主要方法之一，针对高速列车表面湍流状态，该方法可以准确地描述一些不稳定过程中的大尺度效应和小尺度结构，同时不占用过多的计算内存，使运算的周期得以降低，缩短求解周期，是直接模拟方法和雷诺平均模拟方法的完美结合，这也是针对高速列车表面湍流脉动较理想的方法[22].通过对N-S方程进行空间过滤，得到大涡模拟的控制方程，其连续方程与动量方程分别表述为

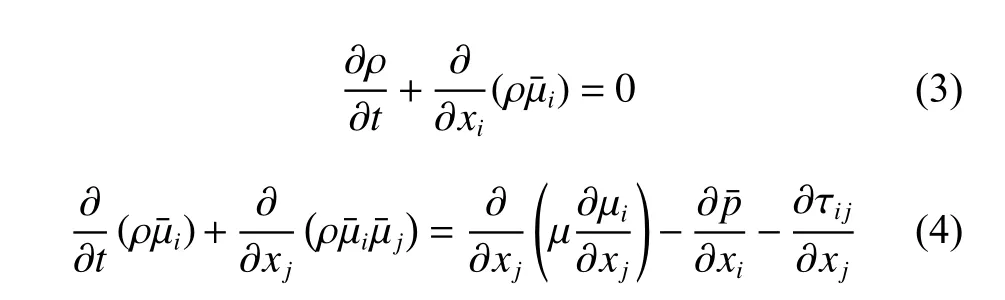
1.2 物理模型分析与建立

本文中采用某型1:10三编组磁浮列车，缩比后车辆尺寸参数为L=8.1 m，W=0.37 m，H=0.42 m.仿真模型计算域的选择直接决定了求解速度和精度，计算域尺寸过大导致计算成本高，反之则计算精度较低.针对明线工况，拟定采用矩形计算域，研究表明，当车头前端计算区域约为1倍车长、车尾后端计算域约为2倍车体长度时，即可满足精度要求，列车车头鼻尖点距入口处8.1 m，车尾鼻尖点距出口15.8 m，计算域总长为32 m.同时流场区域两侧宽度应超过车宽的5倍，流场区域的高度应超过车高的5倍，流场区域宽度为2 m，高度为2.4 m，该计算域模型兼顾了速度和精度，并被广泛应用于明线列车气动载荷的求解[23].对于边界条件，拟定高速列车正前方来流方向截面为入口边界，设置为速度入口，正后方截面为出口边界，设置为压力出口，其压力为标准大气压，列车表面设置为无滑移壁面，地面设置为滑移地面，其滑移速度为列车运行速度.本文中模型不考虑轨道因素，列车及计算域尺寸如图1所示.

1.3 网格划分

考虑到列车缩比模型复杂的轮廓线条，本文中首先采用HyperMesh对列车进行网格划分，以更好地处理因模型轮廓不规则所引起的网格畸形问题.对于磁悬浮列车表面网格，采用三角形与四边形混合网格，在车头与车尾处进行加密处理.其中，针对车头与车尾复杂的轮廓外形，三角形离散网格更符合其表面几何要求，使针对曲面的求解更可靠，极大地减少网格自穿透现象，提高网格质量.车身侧表面光滑，采用四边形网格，使在保证网格质量的同时降低网格数量，为后期仿真节约计算成本.由于列车实体复杂，计算域网格采用四面体网格，配合边界层网格，便可达到较好的模拟效果.

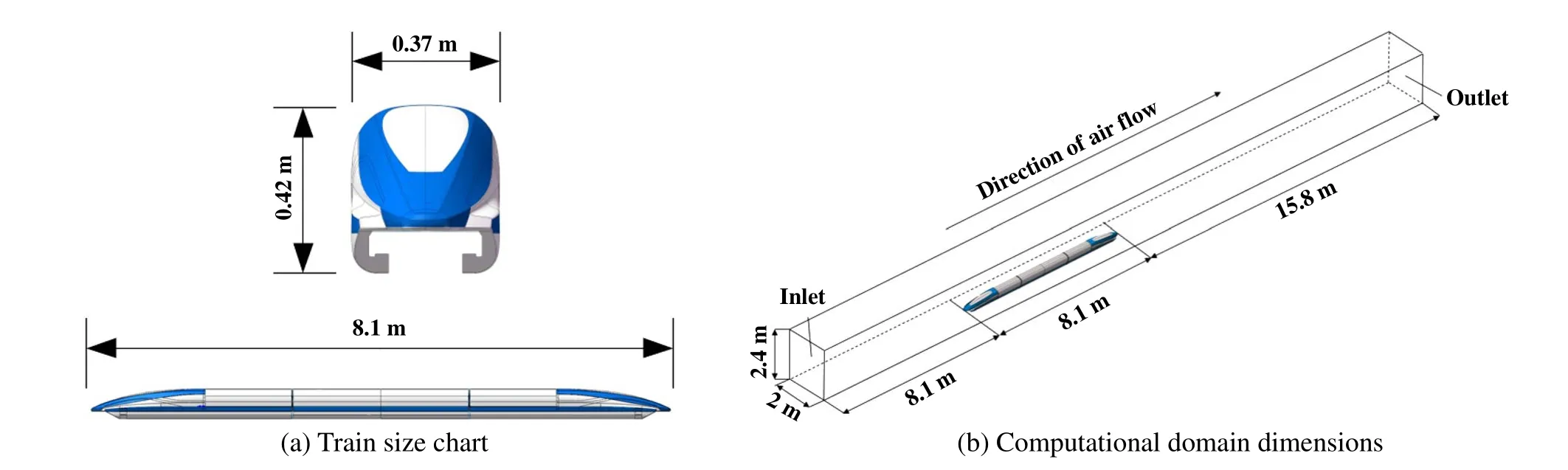
Fig.1 Calculation domain and train size for bright-line operation图1明线工况列车及计算域尺寸

在高雷诺数运动过程中，湍流模型只针对充分发展的湍流才有效，在近壁面处，由于边界层的存在，使得湍流发展不充分，此时湍流模型在该区域无法适用.针对近壁区流体雷诺数较低、湍流发展不充分以及湍流脉动影响不及分子黏性的影响等问题，通过引入边界层网格，并结合半经验壁面函数法，与湍流模型进行配合，以解决近壁区的流动计算问题.对于壁面函数的选择，Fluent中提供了标准壁面函数、非平衡壁面函数及增强避免处理三种壁面函数类型，考虑到高速列车近壁区湍流状态符合标准壁面函数求解要求，能在满足精度要求的同时，降低计算成本[24].因此，本文中采用标准壁面函数来解决近壁区湍流发展问题.根据离壁面法线距离的不同，可将流动划分为壁面区和核心区，壁面区又可分为黏性底层、过渡层和对数律层.由于黏性底层与过渡层厚度极小，因此直接以对数律层的方法处理，为了用公式描述对数律层内的流动，引入无量纲参数，表示第一层节点距壁面的无量纲距离，用公式(5)计算.为保证较好地捕捉湍流边界层内参数变化，应使第一个节点尽量靠近湍流边界层内边界，对第一个网格节点到壁面距离计算，通过公式(6)计算.

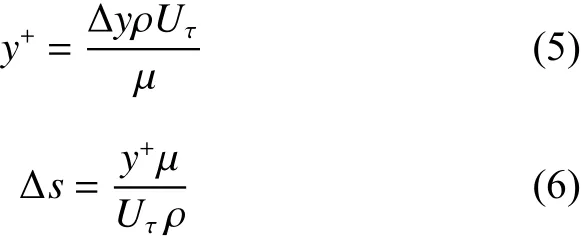
针对600 km/h时速的仿真模型，建立6层边界层，第一层边界层厚度为0.17 mm，并按1.2倍的增长比向外扩散.考虑到网格划分时，在保证求解结果可靠的情况下，降低网格数量，以达到减少计算成本的效果.因此，通过对比网格数量在1 000万至3 000万变化时，数值仿真结果的波动情况，进行网格收敛性分析，最终确定出网格数量在2 200万左右时，可以兼顾计算精度与计算成本要求，如图2所示.

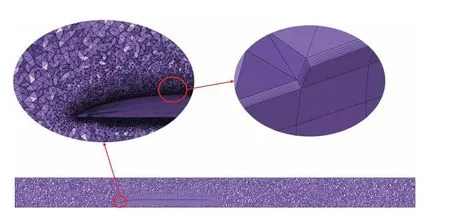
Fig.2 Computational domain grid model 图2计算域网格模型

2 数值模拟分析

2.1 稳态分析

由于高速磁浮列车几何外形存在复杂的流线型设计，运行时气流与列车表面碰撞，产生剧烈的涡流运动[25].列车表面的压力脉动是由涡流的运动引起，本文中通过结合列车表面压力分布与速度分布分析涡流的运动情况，涡流运动强烈的位置其脉动压力变化大.为了准确反应列车表面湍流特性，稳态计算基于标准k-ε模型.该湍流模型在满足收敛性和精确性符合工程要求的同时，极大地降低计算成本，配合半经验公式边界层的使用，可以达到相对较好的精度.

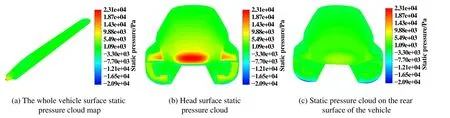
Fig.3 Static pressure distribution of the bright line working condition of Maglev train图3磁浮列车明线工况静压分布图

图3 所示为运行速度在600 km/h时，列车表面稳态仿真静压云图.从中可以观察到，由于列车车头的外形是流线形，在高速运行中，车头正对空气来流方向，鼻尖位置最先与流体接触，空气的流动受到阻碍，使得车头鼻尖压力最大.随后气流从压力最大区域沿车体表面分别流向车底、车身侧壁和车顶，由于车身两侧存在凸起的抱轨，使得气流受到了二次阻碍，但气流的能量产生耗散，使得此处形成的正压区压力值低于鼻锥区域.气流主体部分经由列车车窗至车顶的空气，从鼻尖位置到车身，正压逐渐减小变为负压，在车头向车身过渡处，负压达到最大值.与此同时，较车头与车身过渡区域，压力在车头鼻锥区域变化剧烈，等压线密集，压力梯度大.究其原因，因为车头向车身过渡时曲率不断变化，使得流体绕流速度加快，造成过渡区域压力急剧降低；车头鼻锥处的曲率变化大，压力变化相对集中，随着车头小曲率的流线型变化，表面压力变化不明显.由于能量耗散的缘故，车顶压力呈现降低趋势，车身中间段压力值较小.在三编组列车，车头与车厢和车厢与车尾两两连接处的凹槽内气流量减少，出现局部的压力波动.车身向车尾过渡处出现负压，车尾鼻锥区域出现正压；由于空气黏性的作用和尾部湍流漩涡的影响，使车尾处表面压力较小，且表面压力低于车头.同时车尾鼻尖处压力分布规律与车头鼻尖处相似，呈现等压线密集和压力梯度大的现象.

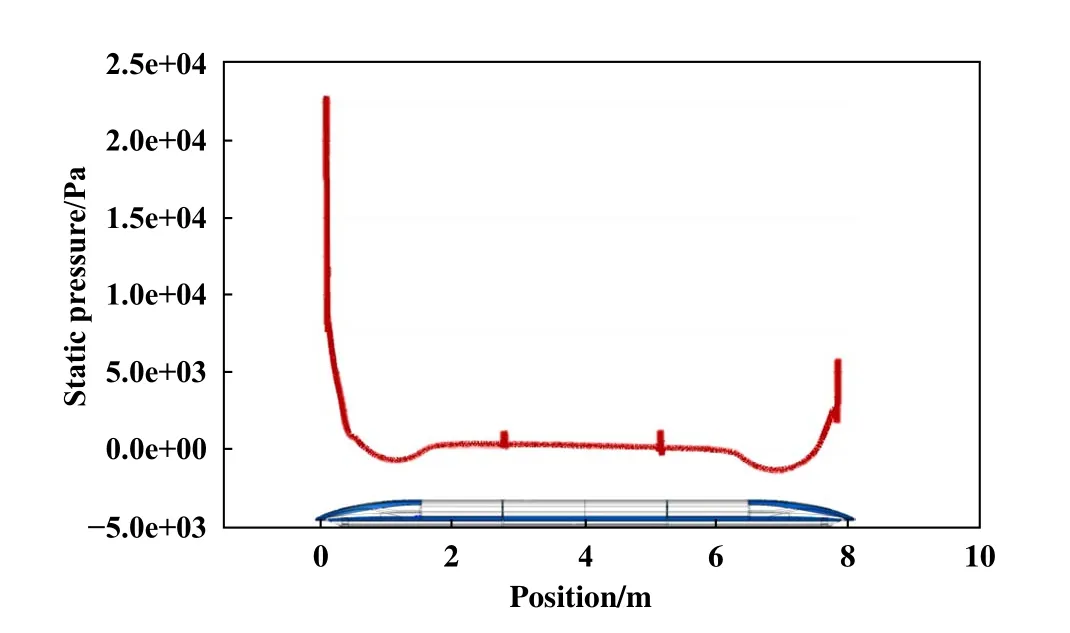
Fig.4 Top midline static pressure distribution curve图4顶部中线静压分布曲线图

取车顶部中间对称线位置，绘制其静压分布规律曲线图(图4).在车头鼻尖位置压力最高，随着表面曲率的变化，在车头与车身过渡位置出现了局部负压，当气流流经车身时，表面压力变为正压，由于能量的耗散使得中间段压力逐渐下降.在车头与车厢连接处和车厢与车尾连接处，过渡凹槽使得截面变化，凹槽内气流量减少，出现压力波动现象.车尾压力分布规律与车头相似，但低于车头部分压力，与压力云图呈现的规律相对应.

为分析列车表面涡流运动情况，取计算域中间截面分析其速度变化规律.如图5所示，气流受头车鼻尖点阻滞作用，速度迅速降低，在鼻尖位置形成滞止区，该位置空气的速度近乎为零.随着气流沿车身向后运动，在车身过渡区域曲率变化较大，加上空气的黏性作用，使得车体表面形成速度梯度较大的附面层.随后，附面层沿车身稳定发展，厚度不断增加.当达到车身向车尾过渡区域，表面曲率的变化导致空气扰动，使得附面层与车体分离.

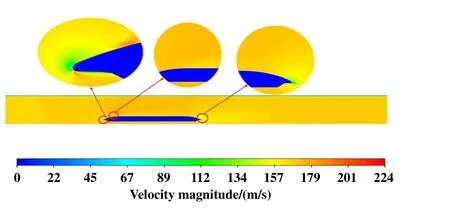
Fig.5 Maglev train surface speed cloud map图5磁浮列车表面速度云图

经上述对列车表面压力分布与速度分布分析，得到了近场气动特性，为了进一步找出其诱导的气动噪声，图6所示为列车表面的声功率级云图.可以发现车头鼻尖处声功率级最高，从鼻锥区域至车身，声功率级呈下降趋势，在车身平滑位置趋于稳定.在车身与车尾流线型曲面过渡位置处，声功率级增高，但幅值低于车头对应位置.从车尾过渡位置到鼻尖处，声功率级呈现降低趋势.为更全面分析列车表面声功率级变化规律，图7所示为列车表面声功率级分布图.可以看出，中列车中间段出现两处数值波动，分别对应车头与车厢、车厢与车尾两两连接处；头车、尾车非流线型区域和中间车厢处声功率级均较小；头车和尾车声功率级数值幅度变化明显高于中间车.

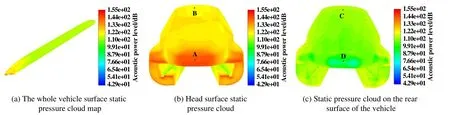
Fig.6 Sound power level distribution of the bright lineworking condition of Maglev train图6磁悬浮列车明线工况声功率级分布图

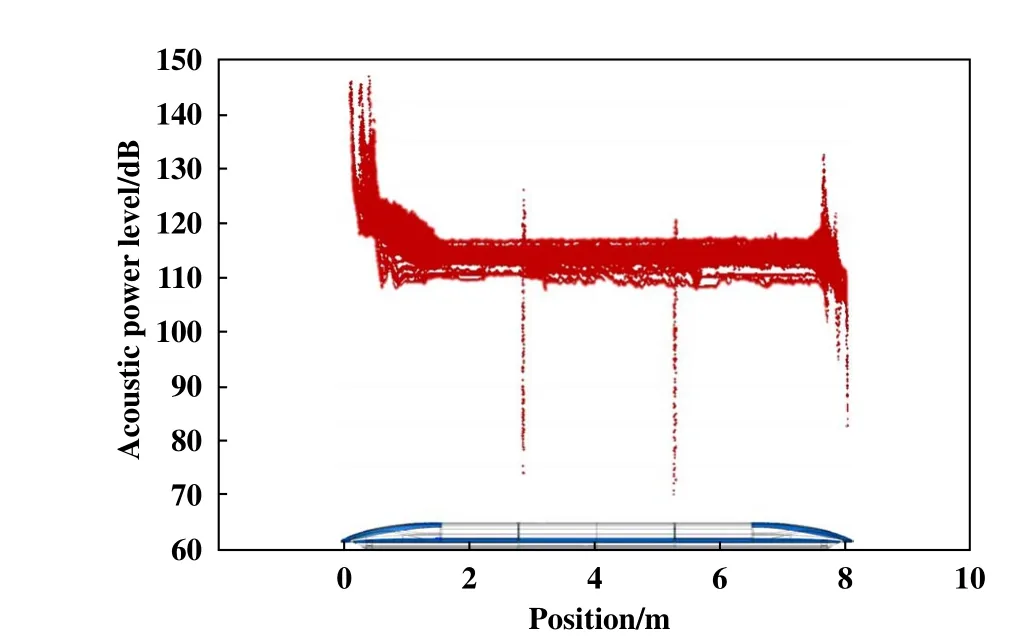
Fig.7 Distribution map of the sound power level on the surface of the vehicle图7整车表面声功率级分布图

综上所述，列车整车噪声源并非单一，其主要声源发生在车头鼻尖、曲率发生较大变化位置.考虑到车头鼻锥区域鼻尖点附近声功率级最高，且在车头与车尾鼻锥区域向车身过渡位置，表面曲率变化大.为捕捉主要声源位置声压级情况，分别设置监测点A、B、C和D，如图6(b)和(c)所示.其中A点为车头鼻尖点，B和C点分别对应车头与车尾表面曲率变化较大位置点.D点为车尾鼻尖点，是除截面突变区域外，声功率级最小区域选取的监测点，该测点的数值可为后续开展暗线近场噪声分析提供对照研究.

2.2 瞬态分析

考虑到磁浮列车表面的气动噪声来源于脉动压力，利用瞬态分析求解，能更好地捕捉列车表面声压级的变化.为开展瞬态分析，采用大涡模拟法，通过数值解方程直接计算大尺度运动，对于不能求解的小尺度运动，则通过建立与大尺度运动之间的关系及相关模型来分析.在构建小尺度湍流运动与大尺度湍流运动之间关系时，合理的选择亚格子模型，可以做出更好的流动预测，对于亚格子模型选用Smagorinsky-Lilly模型，该模型可以在保证计算误差较小的同时，极大地降低计算成本[26].采用FW-H声学模块，同时设置监测车头与车尾处4个特征点位置.瞬态求解的过程中，考虑声场最高频率与时间步长的对应关系和求解步数的关系，设定流场气动噪声的最高频率为2 500 Hz，根据Nyquist采样定理，计算时间步长应小于2E-4，因此本文设置时间步长为1E-4，迭代步数为1 000步(物理时长为0.1 s).在迭代结束后将时域所采集到的监测点信息经过傅里叶变换转换成频域信号，得到车头与车尾监测点声压级曲线.本文中对比了500与600 km/h两速度下各监测点声压级曲线变化规律，仿真结果如图8所示.其中发现在不同速度下，车头与车尾对应位置监测点的脉动压力分布规律基本一致，脉动压力分布频率广泛，没有集中分布在某一频率内，随着频率的增加，脉动压力有逐渐衰减趋势，两处过渡位置监测点由于曲率变化大，所产生的波动较为明显.两种速度下车头鼻尖处监测点的声压级均高于车尾鼻尖处，同一速度下过渡区位置监测点数值较为接近，由于速度的增加，列车表面所产生的气动噪声也越剧烈，呈现600 km/h速度下声压级高于500 km/h下的现象.

3 结论

a.高速磁浮列车表面静压呈现车头与车尾鼻尖位置等压线密集，压力梯度大，表面最大压力达到23 100 Pa，曲率大的位置压力变化明显；在车头与车尾鼻尖、曲率变化较大位置涡流的运动更为剧烈.

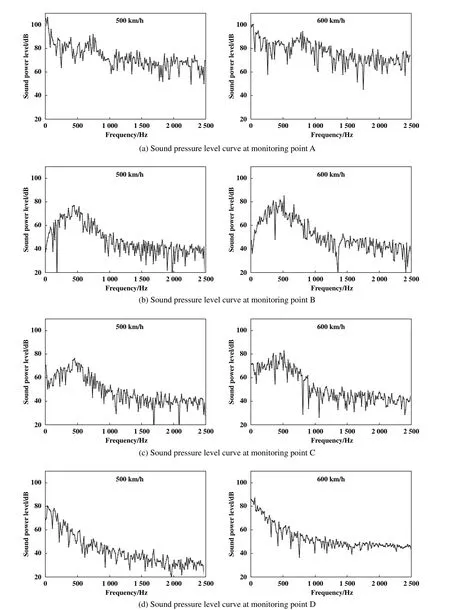
Fig.8 Spectrum of sound pressure level at each monitoring point on the surfaceat different speeds图8不同速度下表面各监测点声压级频谱图

b.高速磁浮列车气动噪声源并非单一，其主要声源发生在车头鼻尖、曲率发生较大变化位置，表面最大宽频带噪声可达到155 dB.

c.不同速度下，列车表面对应位置检测点声压级分布规律相似，近场的气动噪声属于宽频带噪声，没有明显的主频；在表面曲率变化较大位置处会出现气流扰动，导致波动幅度较大，近场气动噪声低频的能量较大，随着频率增加出现衰减趋势；车头鼻尖位置处声压级明显高于车尾鼻尖位置，整体呈现600 km/h速度下声压级高于500 km/h下的声压级.