考虑交通公平的主辅交叉路口半固定相位信号配时优化

傅文翰

（上海理工大学管理学院，上海 200093）

在城市化进程中，城市车辆数目急剧增长，网状分布的城市交通道路形成众多的道路交汇，交通问题越发凸显。城市的交通信号灯，大部分根据路口车辆数量按照默认固定信号周期、固定红绿灯时间和固定相位转换次序的方法[1]。固定配时的信号控制模式使交通效率大大降低。

与此相关的研究主要集中在优化算法的改进，利用智能算法改变不同相位的信号时长。吴啸宇等人构建以车辆延误和停车次数作为优化目标的交叉口信号优化模型[2]。王曈等人建立灰色预测模型预测流率，并以遗传算法对干线交叉口信号灯配时进行续进式协调控制[3]。杨海荣等人提出一种相序可变的实时滚动优化模型进行单交叉口信号控制[4]。然而，相序频繁改变的智能算法方案会使驾驶者思想高度紧张，无法做出及时反应易引起交通事故[5]。

同时，以车辆延误等道路效率作为优化目标，没有充分考虑到作为交通参与者的交通公平性。道路资源配置作为交通公平的组成之一[6]，大部分研究聚焦在不同交通方式间的公平性比较，如公共交通和小汽车等[7]，而缺少对于同类型通行个体之间的公平性衡量。

通过对单交叉路口交通控制情况的分析和讨论，兼顾公平和效率，本研究提出以主辅路控制为核心的半固定相位交通灯配时方案，克服传统配时方案的效率不高和智能算法的公平性欠缺的问题，能够有效对信号灯进行配时优化。

1 研究方法

根据实际情况做如下假设：①不设置行人专用相位，车辆的右转行驶总是可行。②不考虑路口间相互影响。基于上述条件假设，单路口有8 条车辆行驶路线，如图1，建立总体通行效率为主，个体等待公平为辅的优化方案。

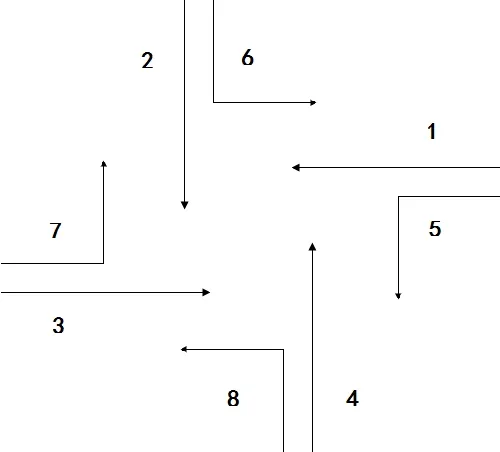
图1 单路口相位图

1.1 总体通行效率为主

同时开放两条路线分称为主路和辅路，由主路决定开放时间和顺序并进行周期性运转。对于单路口，同时只能运行两条路线；每条路线有三条相容辅路，主路与其相容辅路同时开放；所有路线的三条相容辅路两两冲突。结合主辅路的固有性质，确定主辅路开放的原则，其重要性依次递减：

（A）当前主路的三条相容辅路不包含上条主路。

（B）当前主路不属于上条主路的相容辅路。

（C）当前主路与上条主路相容辅路重迭数最小。

在固定主路顺序的前提下，满足开放原则记0，不满足记1。主路每次转换对应三进制数字称为权重，所有路线相应权重之和最小为最优。因为只有从直道路线转移至直道路线，权重才会是（001），而在一个开放周期内，必有从直道转至弯道和从弯道转回至直道，所以8 个或7 个（001）均不可行，最小的权重和就只能是（001）*6+（002）*2。

以路线1 为例。从路线1 转移至弯道路线是1-＞7或者1-＞6。若1-＞6，只能接续6-＞7-＞8-＞5。从路线5转至直道路线可以是5-＞3 或者5-＞4，若是5-＞3，则后续不能返回到最初的路线1，只能开放5-＞4-＞2-＞1。若1-＞7，情况类似。从而只有1-＞6-＞7-＞8-＞5-＞4-＞3-＞2-＞1 和1-＞7-＞8-＞5-＞6-＞4-＞3-＞2-＞1 是权重最小的开放顺序。确定主路开放顺序后，再选择其相容辅路进行开放，以提升总体方案的交通公平性。

1.2 个体等待的交通公平性为辅

考虑到单一路线的开放时间必须有上下限，以保障通行个体的交通公平。即使某路线只有一辆车等待，也要有一定时间让其通行，即使某路线堵塞，也不能一直通行。

除了考虑主路上等待车辆的数目之外，利用辅路与主路车辆数的相容性来影响开放时间。由于两条路线上等待的车辆数完全相等的情况较难发生，当两者等待数量之差小于较大数量的三分之一时，就视其为相当。设计在主路开放时其相容辅路开放的三原则：某条辅路的待过车辆与主路数相当，则开放；三条辅路待过车辆数之和与主路相当，则三依次放行；三条辅路待过车辆之和远少于主路，则跳过放行。

1.3 半固定相位不固定时间配时优化

若相位不固定，在每个周期的结束处，由于相位的不固定性，很难保证每个相位对路口使用的公平性，从而影响到驾驶者的情绪变化，致使交通事故频发[9]。因此提出了主辅相位的半固定相位的方案，同时选择不固定时间模式调控信号配时。具体方案如下：

（A）若当前主相位要放行，此次放行时间为该主相位所有车辆放行完毕的但不超过预设的最长放行时间。

（B）相应的三条辅相位中若有一条与主相位相当，则该辅相位同时放行，并于到达主相位时间后无条件关闭。

（C）相应的三条辅相位的车辆数若与主相位相当（大于50%），则此次三条辅相位相继放行，并于到达主相位时间后关闭。

（D）若主相位无车辆等待，则跳过此次主相位的放行。

（E）若与主相位对应的三条辅相位的车辆之和远小于主相位车辆数（小于50%），则跳过此次主相位的放行，并且下一周期无条件放行，且最长放行时间临时变更为现有的两倍。

2 模型验证

一定时间内到达某一断面处的车流量是随机的，通过大量交通观测发现，在一定的观测周期中到达的车辆数服从泊松分布[8]。设计三种不同的道路情景：

情景一：模拟城市中上下班高峰时段，单一的进城方向（出城方向）车流量很大，而相反方向的车流量很小。在此种情况下，八个相位设计的泊松参数gama（辆/2s）：0.333300，0.166700，0.111100，0.083300，0.166700，0.083300，0.055560，0.041670。

情景二：模拟城市常规时段，八个相位的车辆相当，但车流量适中。在此种情况下，八个相位设计的泊松参数gama（辆/2s）：0.166700，0.142900，0.125000，0.111100，0.083330，0.071400，0.062500，0.055560。

情景三：模拟节假日等严重堵塞时段，八个相位的车辆相当，但严重累积。在这种情况下，八个相位设计的泊松参数gama（辆/2s）：0.1667000，0.166700，0.166700，0.166700，0.166700，0.166700，0.166700，0.166700。

在单路口一小时的时间内，分别在三种道路情景下，运用三种不同的放行模式重复100 次模拟，前两种方案中最大放行时间为40s，方案三中选取的固定时间为30s。实验得出了实际吞吐量的平均值，如表1。

表1 不同方案平均吞吐量

高峰时段，单方向车辆多而相反方向车辆少。此情景下，半固定相位不固定时间方案的优势充分体现出来，实际通过率明显高于固定相位不固定时间方案以及固定相位固定时间方案，通过率分别提高14.4421%，24.6923%。

常规时段，各相位车流量相当，总车流量适中，此时半固定相位不固定时间方案的优势不像高峰时段那样显著，但平均通行量分别还是提高9.6580%和11.4460%。

严重堵塞时段，由于各个相位车辆均严重累积，此时半固定相位不固定时间方案与固定相位不固定时间方案的效果相当，均比固定相位固定时间提高1.6647%。

综上所述，在各种道路情景下，半固定相位不固定时间方案均优于固定相位不固定时间方案、固定相位固定时间方案。特别在前两种情形下，优化效果有显著提高。

3 结论

本研究同时考虑通行效率整体提升和个体交通公平的现代城市社会需求，建立总体通行效率为主，个体等待公平为辅的主辅路半固定配置优化方案，以改善现有配时方案的不足。通过程序模拟分析，结果证明相较于传统信号配时方案，单位时间内车辆通过率有效提升。由于实验条件限制，本研究使用模拟数据作为验证，未来可以使用真实交通大数据做进一步研究。此外，未来研究可以对信号灯配时优化问题中交通公平性的衡量方式做进一步探索。