激光探测双胶合透镜校正光学像差方法

孟展鹏，陈荷娟，张祥金

(南京理工大学 机械工程学院，南京 210094)

1 引言

激光制导武器具有精度高、抗干扰能力强、结构简单、成本低等特点，并易与其他制导系统兼容，现今已广泛应用于多种武器装备，并在近些年世界局部战争与冲突中，发挥着越来越重要的作用。在常规武器制导化的发展背景之下，考虑将激光半主动目标探测技术应用到巡飞武器上来，是解决巡飞武器制导化改造的成本与飞行轨迹修正精度之间矛盾的一种可行途径[1-3]。

光学系统是半主动激光导引装置的重要组成部分，徐大维，刘宇承等学者使用多个单透镜(4个及以上)组成折射式透镜组解决光斑像质不足的问题。周晓斌，宋岩峰等[4-6]在多模探测光学系统设计中，设计折反式光学系统来提高生成的光斑像质。实际光学系统的对物体的成像是不完善的，像差则是这种不完善程度的描述[7-9]。对激光光学像差的研究可以对光学系统相应参数进行优化，以提高激光系统的性能。任广森[10]使用数值仿真的方法，研究得出部分球差、慧差和畸变等初级像差会对光聚焦场光强分布产生明显影响的结论。江恒等[11]则重点研究了球差对高斯光束成像的影响，得出球差越大对光束像方束腰半径影响越大的结论。Kotov 等[12]则提出基于可控表面形状的可变形反射镜的主动波前动态像差校正方法[13]。

目前的相关研究在解决制导装置光学系统小型化和提高光斑像质的问题上，大多学者使用较多数量折射透镜或者较大尺寸的反射结构，甚至使用成本较高的非球面透镜和可变形反射镜来减小像差。针对制导装置光学系统小型化和提高光斑像质的问题，基于初级像差理论，同时结合仿真与像质评价软件，提出通过设计双胶合透镜组取代传统设计中的单个单透镜的方法，校正单透镜光学系统存在的初级像差。

2 半主动激光探测原理

半主动激光探测的工作原理是由弹外激光指示器发出经特定周期编码的激光照射到目标上，当巡飞武器飞近至满足导引装置捕获目标作用距离时，导引装置光学系统捕获目标物体漫反射的激光信号在四象限探测器上，如图1所示。在激光半主动导引头的工作过程中，光学系统的主要作用是接收和汇聚由目标反射的激光到四象限探测器上。控制系统对四象限探测器获得的光斑能量数据进行分析处理，判断出目标的角度和位置信息[1]。

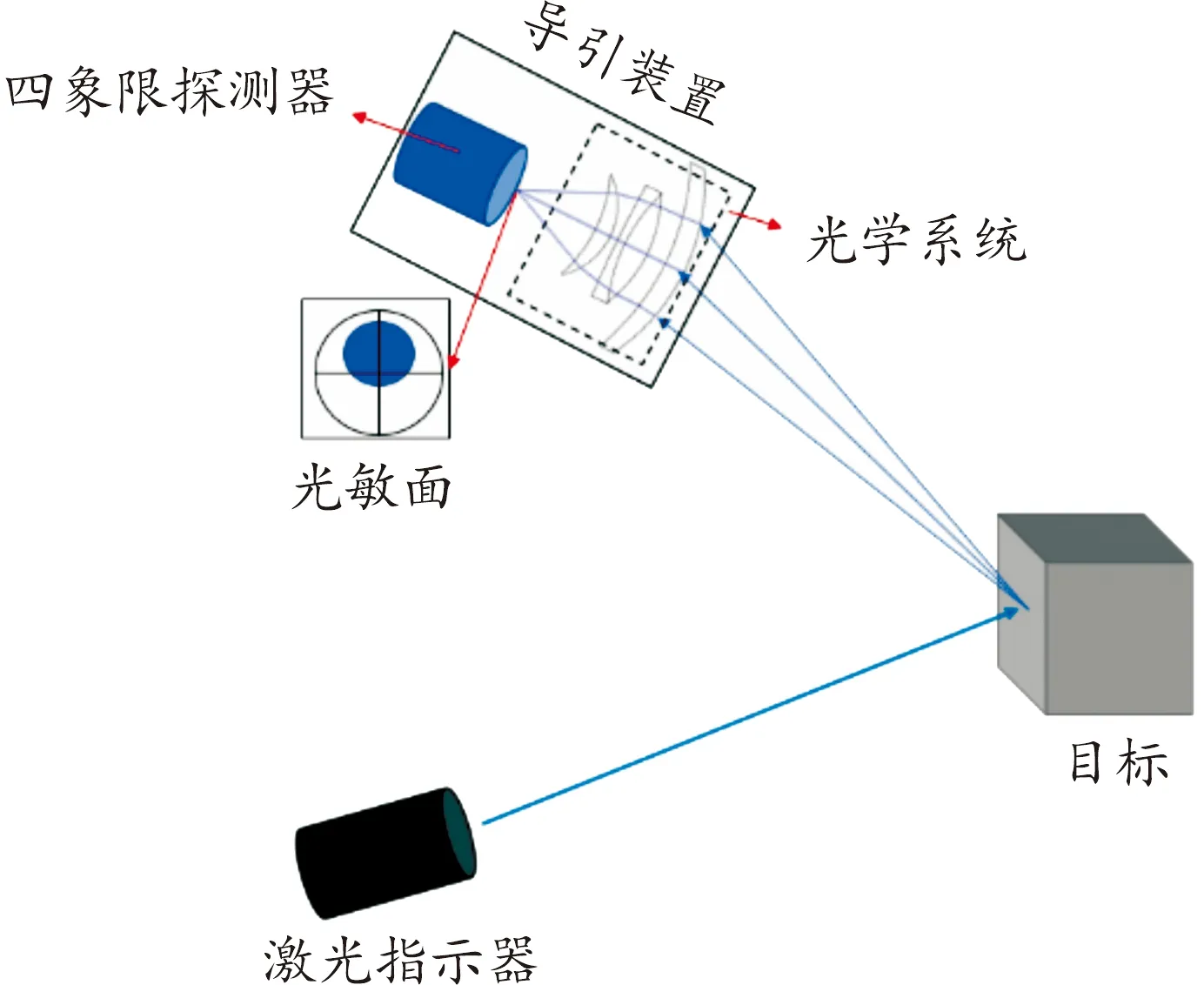
图1 半主动激光探测原理

通常情况下，对巡飞武器的可靠探测距离要求在600～800 m，为了能够尽量缩短从捕获目标到打击目标的时间差，就要求机载系统能更快，更精确的计算出弹目之间的空间位置关系，而四象限探测器光敏面上的光斑是计算空间位置的唯一来源。高质量，高精度的光斑能有效缩短机载系统在计算上花费的时间。

在光学系统设计中，一项重要工作就是校正光斑的光学像差，使成像质量达到技术要求。为了加速设计过程，提高设计质量，人们对像差的性质、像差和光学系统结构参数的关系进行了长期的研究，取得了很多有价值的成果，这就是像差理论[14]。

3 初始光学系统理论计算

3.1 光学系统指标

巡飞武器导引装置光学系统的主要设计指标为：

1)工作波段：(1 064±2.5)nm；

2)接收透镜通光口径：D≯φ32 mm；

3)接收视场：2ω=±10°±0.5°，线性区不小于±3°；

4)四象限探测器光敏面直径：D1=10 mm；

5)作用距离不小于800 m，识别距离不小于500 m。

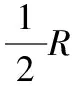
在主视场光斑半径为2.5 mm，±3°视场范围为线性区间的情况下，为保证始终位于四象限探测器光敏面内，取最大3°视场下，光斑的半径最大值3.125 mm，此时，通过计算可得，光斑像高最y大为1.875 mm。同时，当主光线位于四象限探测器光敏面中心，导引头光学系统的焦距与导引头成像像高存在如下关系：

y′=f′tanω

(1)

式中：f′为光学系统有效焦距，ω为最大视场角。计算得出，设计的光学系统焦距要求在35.78 mm以内。

同时根据导引装置的空间尺寸要求，初步确定入瞳直径：D=φ30 mm；四象限探测器光敏面到光学系统中心的距离为25 mm。根据几何光学理论计算，光学系统焦距约为30 mm。

3.2 初始光学系统计算

根据前面理论计算的参数可知，初步确定设计的实际光学系统的有限焦距为30 mm，入瞳直径为30 mm，线性视场角为±3°。

根据设计经验及设计指标要求的设计尺寸，初步确定整流罩透镜物方和像方面的曲率半径为50 mm和60 mm。由于光学系统最后一块透镜承担主要的光线折射工作，初步确定透镜的物面曲率半径为20 mm，透镜的有效焦距为60 mm，玻璃材料为K9玻璃。根据公式[16]：

(2)

式中：f为透镜焦距；n为玻璃材料折射率，数值为1.516 7；R1为物面曲率半径；R2为像面曲率半径；d为透镜厚度。计算得出，整流罩的有效焦距约为443mm，折射镜的像面曲率半径约为52.52mm。

透镜组整体有效焦距计算公式[16]为：

(3)

式中：f为透镜组有效焦距；f1为透镜1有效焦距；f2为透镜2有效焦距；d′为两透镜之间的距离。计算得出，双胶合透镜的焦距约为82mm。

Q=c2-1

(4)

为单透镜的像面曲率。在归化条件下单透镜的总光焦度，因此

φ=(n-1)(c1-c2)=1

(5)

在玻璃折射率n确定后，由式(4)Q一定，则确定，也随之确定。像差特性参数，和Q存在以下关系：

(6)

(7)

(8)

式中，P0、Q0只是折射率n的函数。

初级像差方程组总共由7个初级像差方程组成，总共有4个未知参数P、W、C、μ，其中C是色差参数。本文中是单色激光，故不考虑；μ通常取经验值0.7，因此一般情况下，求解光学系统的单色像差只需要2个已知量即可，本文中选择初级像差中的球差及慧差作为计算对象。

球差计算公式为：

(9)

慧差计算公式为：

KS′=[∑hZP-J∑W]/(-2n′u′)

(10)

光学系统整流罩和折射镜都属于单透镜，经计算，两者总共产生的球差及慧差为δL′=-1.37×104mm，KS′=-0.400 4mm。

因此，需要设计双胶合透镜来补偿2个单透镜产生的初级像差。双胶合透镜的设计光学特性可以总结为，焦距：f′=82mm，通光直径：D=30mm，线性视场角：2ω=6°，光阑位置与主折射镜物面重合。计算过程可以叙述为：

(11)

由于光阑与物面重合，因此：

hZ=0

(12)

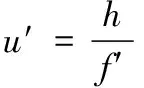
(13)

y′=-f′tanω

(14)

J=n′u′y′

(15)

根据对整个透镜系统的像差要求，求出双胶合透镜的像差和数。

SⅠ=-2n′u′2δL′

(16)

SⅡ=-2n′u′SC′y′

(17)

同时，对单个薄透镜组有：

SⅠ=hP

(18)

SⅡ=hZP-JW

(19)

由h=15mm，f′=82mm，因此有：

(20)

(21)

(22)

由于探测器光学系统本身对无限远物平面成像，因此无须再对物平面位置进行归一化

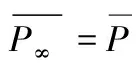
(23)

(24)

根据P0选择合适的玻璃：

(25)

根据计算得出的P0值，在玻璃库中选择合适的玻璃组合。本设计选择的玻璃组合为成都光明生产的H-K9L和H-BAF8。

H-K9L：nD=1.516 728;v=64.20

H-BAF8：nD=1.647 52;v=33.84

(26)

φ2=1-φ1

(27)

(28)

(29)

(30)

(31)

由此得到：r1=0.684，r2=-0.395 4，r3=-1.198 0，以上半径对应焦距等于1，将它们乘以焦距f′=82 mm，得到最后的半径为：

r1=56.088 mm;r2=-32.422 8 mm;r3=-98.236 mm

双胶合透镜的初始结构尺寸计算完成，结合前文计算的整流罩和折射镜的结构尺寸，光学系统整体初始结构尺寸计算完成。使用初级像差理论进行计算，舍弃了包括透镜厚度，透镜边缘厚度等因素的影响，因此初始光学系统往往不能满足设计要求，因此需要将初始光学系统导入Zemax软件进行仿真优化和像质评价。

4 光学系统仿真优化和像质评价

Zemax软件进行光学系统仿真的基本流程如图2所示。

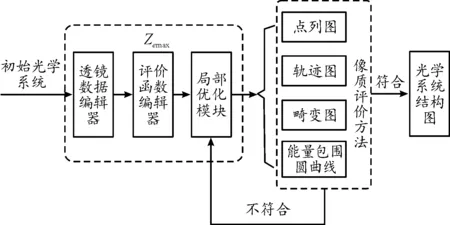
图2 光学系统仿真基本流程

Zemax通过构造评价函数(merit function)，并采用一定的算法计算评价函数的取值。评价函数由系统所设定的操作数构成，其定义式为

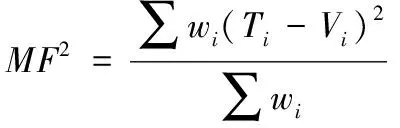
(32)

式中：wi为各操作数的权值，表示某个操作数在评价函数中的比重，是一个相对量，没有特定大小；Ti为操作数设定的目标值；Vi操作数的实际值。显然，评价函数越小，系统越接近于理想设计。在本设计中，设置有效焦距(EFFL)、球差(SPHA)、慧差(COMA)和畸变(DIST)4个操作数在评价函数编辑器里目标值，并设置相对权重值为50、10、100、50，依次按照优化方法的严格性使用局部优化(optimazation)、全局搜索(global search)和锤形优化(hammer optimazation)对光学系统物理结构进行仿真。

将数学计算得到的初始光学系统结构参数输入Zemax软件的透镜数据编辑器，最终得到光学系统如图3、图4所示。本设计光学系统的主要参数为：入瞳直径为30 mm，从入瞳光阑到光敏面的距离是45.5 mm。光学系统相关参数，满足设计指标要求。

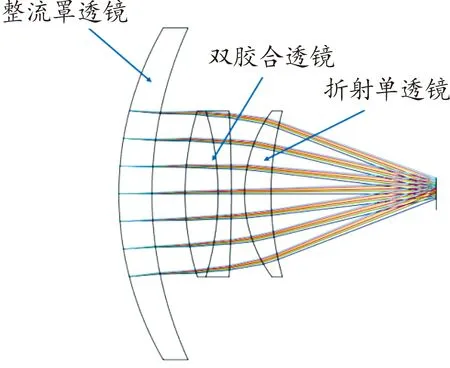
图3 光学系统2维结构

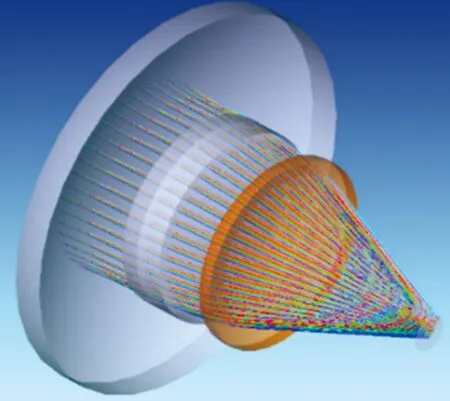
图4 光学系统3维结构

光学系统的第一块透镜为整流罩，用以减小巡飞武器飞行过程中遇到的空气阻力，同时对整个透镜组起到保护作用。第二块透镜是计算设计出的双胶合透镜，用以对整个光学系统产生的单色像差进行补偿，同时在双胶合透镜上的物面覆盖滤光涂层或者滤光薄膜，对不需要进入光学系统的杂光进行滤除。第三块透镜是计算设计的单透镜，和双胶合透镜进行配合进而生成光学系统的目标焦距。

使用Zemax软件读取光学系统成像光斑的像差系数，如表1所示。表中显示的是光学系统的实际像差，初级像差是实际像差的一部分。

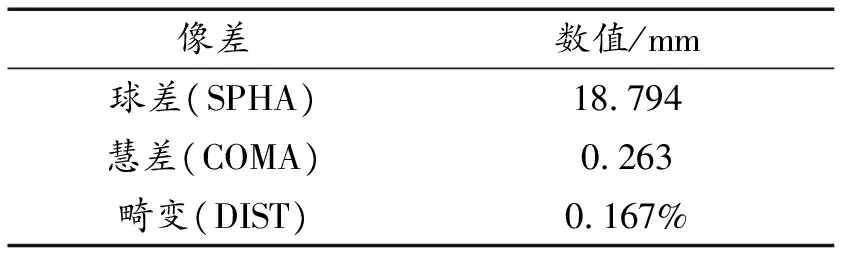
表1 像差参数

从前文理论计算结果和表中结果对比可以看出，在光学系统中引入双胶合透镜可以有效校正单透镜成像带来的像差，而使用单透镜或透镜组的形式难以在保持和双胶透镜同样空间大小时，实现对其他光学系统中其他单透镜的像差校正。

使用Zemax软件携带的像质评价功能对设计的光学成像品质进行评价。光学系统成像在光敏面位置上的像面点列图如图5所示。

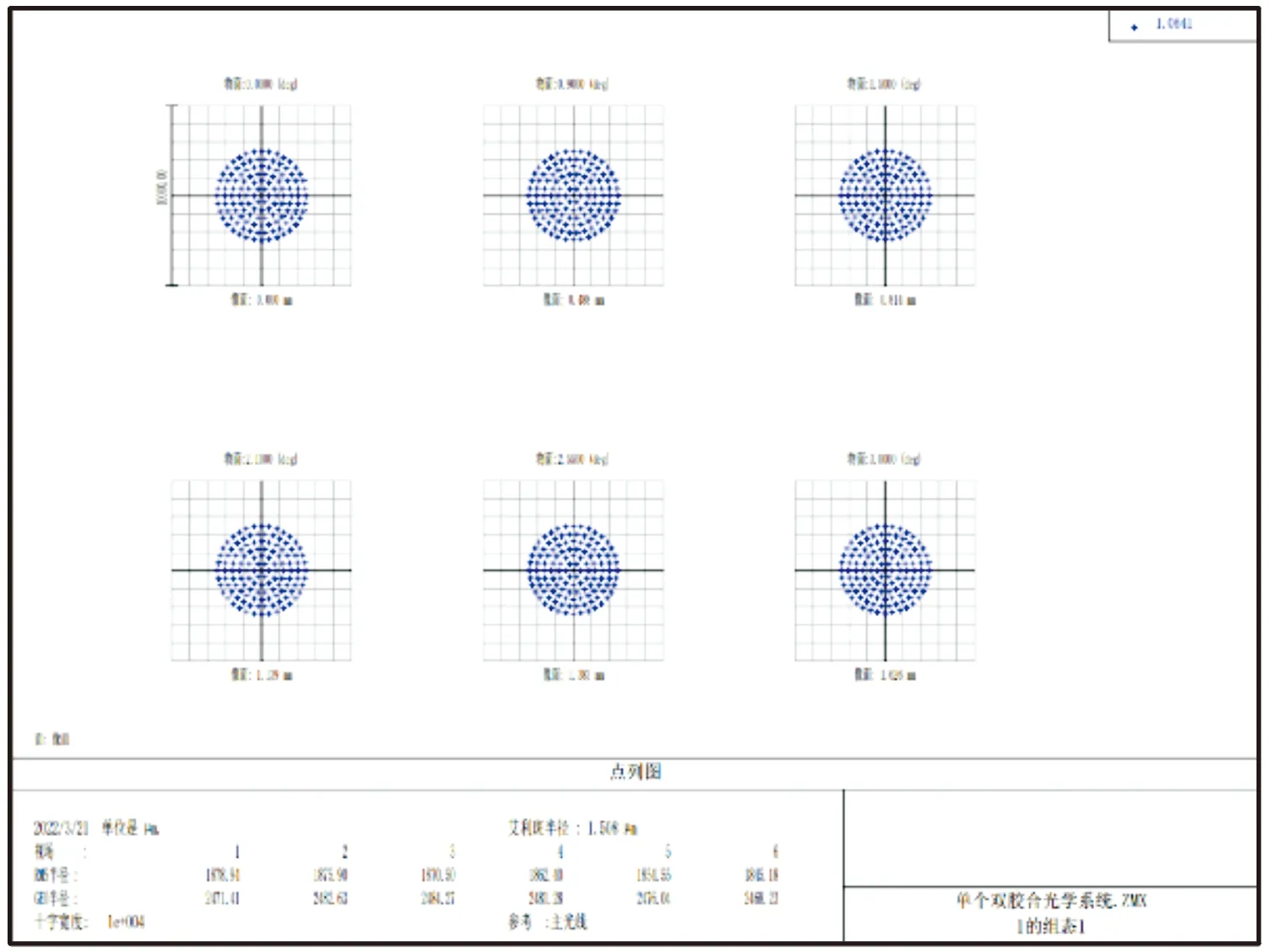
图5 成像光斑点列图

在距离最后一块透镜像面约21.5 mm的位置，成像出直径约5 mm的光斑，比预设计位置超出1.5 mm，在设计尺寸接收范围之内。点列图反映了在6个不同视场下，光斑在四象限探测器光敏面上的形状信息。在点列图中，以主光线作为参考，最大视场的像高为1.644 mm，小于理论计算像高 1.875 mm，同时与理论像高接近，满足设计要求。切换点列图参考至光学系统质心，可以得到最大视场的像高为1.699 mm,同样小于理论计算像高。同时对比2种参考下的像高位置，发现最大视场情况下，像高差为Δ=0.055 mm。光学系统的实际焦距为35.4 mm，由式Δθ=Δ/f′，计算得出角度误差为1.55 mrad，满足光学系统设计对测角精度的一般要求，说明光敏面上成像的光斑圆整度比较好[6]。

图6为光敏面上光斑痕迹图，显示了0°、0.9°、1.5°、2.1°、2.55°、3°六个视场的光斑在探测器光敏面上的位置，同时显示出光敏面和光斑的尺寸。从光迹图中可以看到最大视场3°时，光斑在探测器光敏面上四个象限内均有分布，同时光斑与边缘几乎与探测器光敏面的边缘重合且未超过光敏面范围。

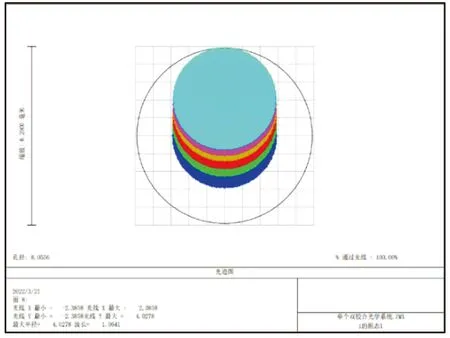
图6 光斑轨迹图

对激光导引头而言，其激光系统线性区的畸变一般要求不超过±5%，才能满足线性度的要求。图7是本光学系统在线性区内的场曲和畸变曲线[6]。分析趋势图可知，在最大视场3°时，光学系统的畸变达到最大值0.167%，光敏面的光斑像基本和实际光斑没有畸变像差。

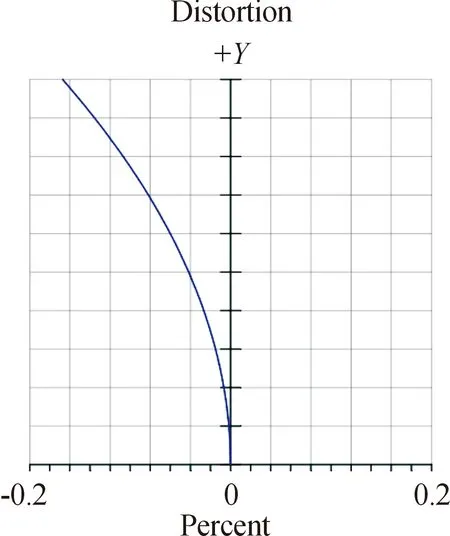
图7 畸变

对于光敏面上光斑能量的分布可以用包围圆能量分布曲线来分析，他描述了在光敏面上光斑的能量随光斑半径的分布情况。假设光斑在光敏面上的能量分布是均匀的，设光斑内的能量分布密度是，则光斑的总能量为：

E=e×π×r2

(33)

分析函数，不难得出，当光斑在光敏面上能量分布绝对均匀时，为常数，光斑的总能量与光斑半径为二次函数关系。所以当光学系统的包围圆能量曲线越平滑，越接近二次函数曲线，则说明光斑在光敏面上的能量分布越均匀。图8显示了0°、0.9°、1.5°、2.1°、2.55°、3°六个视场的包围圆能量分布曲线。

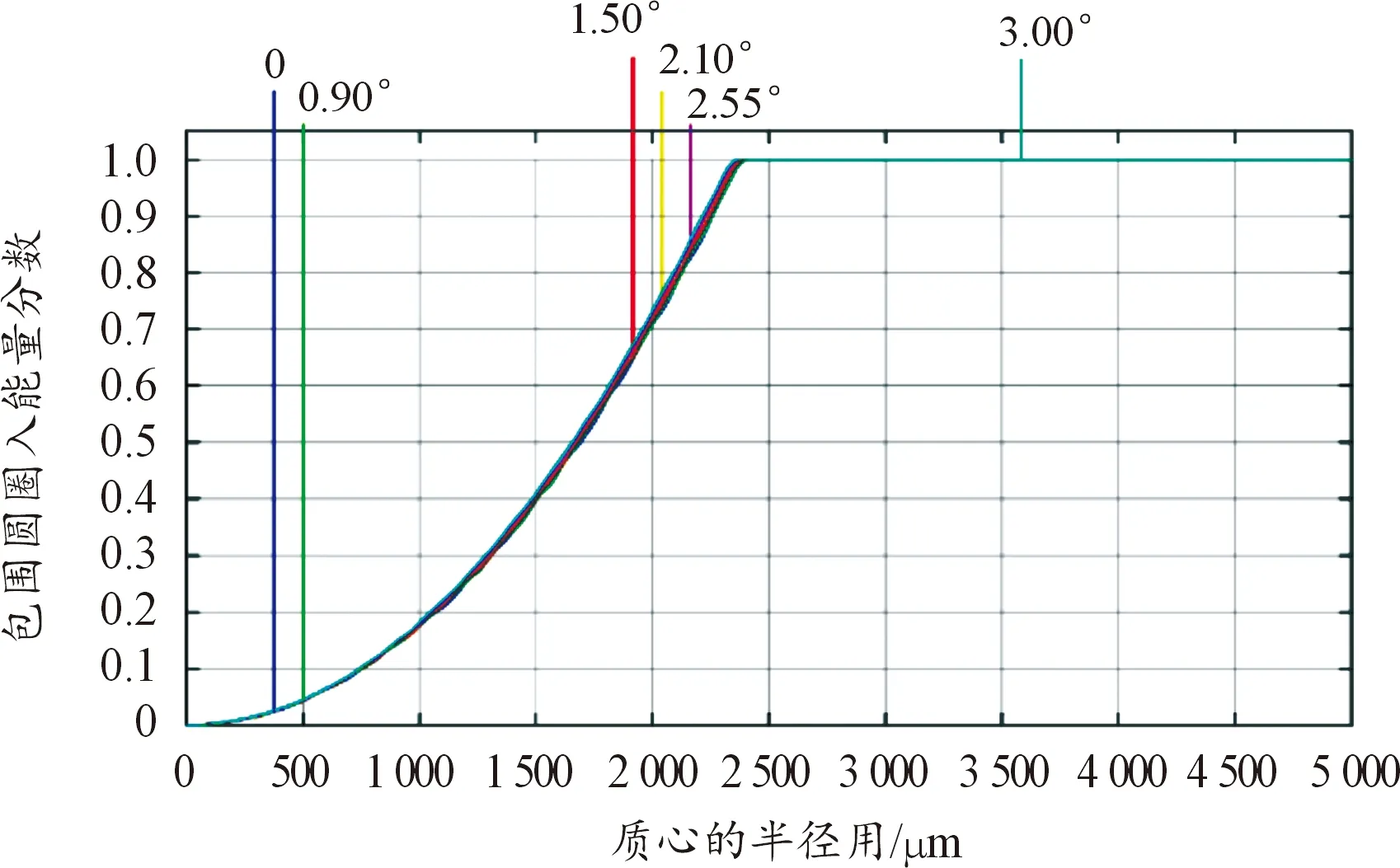
图8 光学系统的包围圆能量曲线

将Zemax圈入能量曲线中的上升沿部分的数据导出到数据分析软件当中，使用数据分析软件对曲线上升沿数据进行拟合，将6个视场的曲线重现画出，如图9所示。

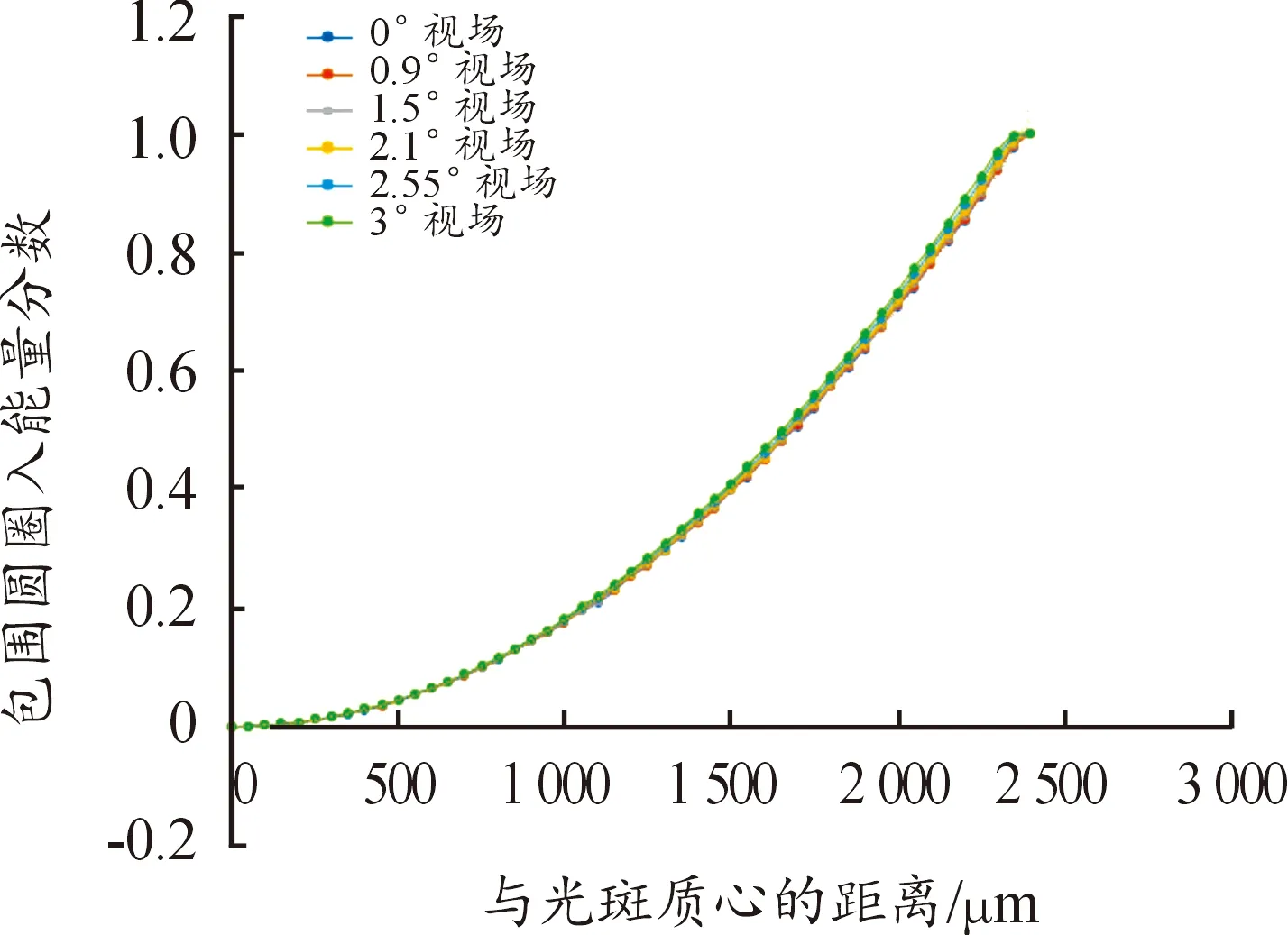
图9 包围圆能量分布图

数据分析软件对0°、0.9°、1.5°、2.1°、2.55°、3°六个视场数据拟合出的函数曲线分别为：

y=2×10-7x2-2×10-6x+0.000 2

y=2×10-7x2-1×10-6x+0.000 3

y=2×10-7x2-9×10-6x+0.000 3

y=2×10-7x2-2×10-6x+0.001 1

y=2×10-7x2-4×10-6x+0.001 7

y=2×10-7x2-9×10-6x+0.003

通过对函数的观察，不难发现6个视场的能量分布曲线非常接近，且一次项系数和常数项非常小。忽略一次项和常数项，则6个视场的能量分布曲线都可以拟合成，实际光斑在光敏面上的能量分布与理想光斑的分布情况较为符合，能量分布的均匀性能满足四象限探测器的要求。

5 结论

1)本文中设计的双胶合光学系统，将传统的单透镜替换为尺寸空间接近的双胶合透镜，以较小的空间尺寸产生更小的光学像差；

2)利用Zeamx像质评价软件验证了双胶合光学系统在保证像质的同时，生成的光斑尺寸、圆整度、系统畸变以及能量分布均匀性均满足巡飞武器用激光半主动制导装置的指标要求。

3)双胶合透镜在半主动激光光学系统上的设计应用，可以有效地减小光学系统的固有像差，为未来的产品设计提供了参考。