光伏机组虚拟惯量控制下电力系统频率特性分析

颜湘武，张世峥，贾焦心

（华北电力大学 河北省分布式储能与微网重点实验室，河北 保定 071003）

0 引言

为完成“碳中和·碳达峰”的目标，风电、光伏等可再生能源得到快速发展。随着光伏等可再生能源发电的快速发展，常规火电机组的退出，系统的惯性支撑和调频能力大大减弱，发生扰动后系统 的 稳 定 性 变 差[1]～[4]。

通常有两类方法可以提高高渗透率可再生能源系统的频率稳定性。一是通过优化常规火电机组控制提高系统的调频能力。文献[5]提出了一种火电机组动态一次调频控制策略，针对不同的频段，采取不同的调差系数值，以此来提高火电机组的一次调频能力。文献[6]考虑新能源不同渗透率下系统的阻尼特性和频率约束，提出一种火电机组惯性参数优化方法，能够改善系统在一般功率扰动下的调频性能。然而，在高渗透率场景下，常规火电机组的调频能力有限，提升可再生能源机组的调频能力尤为重要。二是要求可再生能源机组加入惯量支撑、频率调节等辅助功能，以此提高电力系统的安全稳定性，打破新能源渗透率不能提 高 的 限 制[7]～[9]。

目前，部分高渗透率国家、地区已明确要求可再生能源发电机组必须具备一定的参与电网调频能力[10]。为了实现参与电网频率调节，新能源发电机组须要配置储能装置[11]～[15]或采用有功备用控制，为参与调频预留一定的备用容量。文献[16]将光伏电源通过虚拟同步机技术与电网相连，并验证了其在离网和并网模式下的有效性。文献[17]，[18]提出有功备用运行机制，可以实现光伏机组减载运行并参与电网的频率调节。为了对可再生能源高渗透率系统的频率稳定性进行评估，文献[19]建立了包含常规机组和可再生能源机组的电力系统频率响应模型，计及RoCoF和最大频率偏差两个指标约束，提出一种估计可再生能源占比的方法，仿真得到所研究地区的渗透率只能达到36%。可再生能源占比难以提高的原因，在于该模型的建立并未考虑可再生能源机组的惯性支撑和一次调频能力。文献[20]提出了考虑可再生能源一次调频能力的可再生能源占比极限值计算方法。文献[21]提出了同时考虑风电机组惯量和一次调频响应的风电穿透功率极限计算方法，并且计及了稳态频率偏差和RoCoF两个频率指标约束，但是随着电网规模的扩大，采用该方法进行计算时的模型阶数和计算复杂度将大大增加。

本文搭建了含光伏机组的3机9节点系统模型。建立计及可再生能源机组惯量支撑和一次调频能力的电力系统频率响应模型，定量分析系统的频率稳定性。重点对比分析了不同渗透率场景下的系统频率响应特性，为高渗透率场景下的可再生能源机组调频控制参数的选取，提供参考依据。

1 频率响应建模

光伏发电系统结构主要由光伏阵列、直流母线电容、逆变器及滤波器组成。光伏电站配置储能参与调频的系统结构如图1所示。

图1 配置储能的光伏发电系统结构图Fig.1 Structure diagram of photovoltaic power generation system with energy storage

根据电力系统频率调节原理，储能装置通常采用虚拟惯量控制参与频率调节。其中，通过反馈频率变化率实现惯量支撑控制，并通过有功功率-频率下垂控制实现配置储能的光伏发电系统一次调频功能。光伏和储能系统的控制策略参考文献[22]，[23]。储能系统参与惯量支撑 ΔPes1和一次调频控制的功率参考值 ΔPes2分别为[24]式中：h为新能源惯性时间常数；d为新能源一次调频控制系数；Th为新能源惯量支撑环节的滤波时间常数；Td为新能源一次调频响应的时间常数。

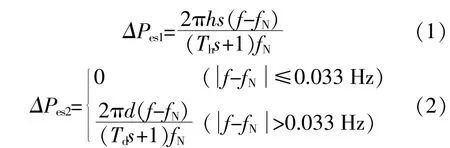
忽 略 一 次 调 频 死 区 的 影 响，由 式（1），（2）建 立光伏机组虚拟惯量控制下频率响应模型，可得到新能源的惯量支撑与一次调频控制模型的传递函数 分 别 为his/1+sTh，di/1+sTd。

在同步发电机原动机、调速器的经典传递函数的基础上[19]，结合负荷对频率控制的影响，并考虑了新能源参与惯量支撑与一次调频的控制模型[24]，由此得到多机电力系统频率响应的传递函数，如图2所示。应用该模型能够分析新能源电力系统的频率响应特性。

图中：TG为调速器时间常数；R为调速器的调差系数；TRH为汽轮机再热器时间常数；FHP为再热系数；TCH为高压涡轮时间常数；H为惯性时间常数；D为阻尼系数；Δω为系统频率偏差；ΔPL为负荷扰动。

当系统有功功率发生不平衡扰动时，频率就会发生变化。研究高比例新能源对系统频率变化动态过程的影响时，通常用最大RoCoF幅值、最大频率偏差、稳态频率偏差等指标进行衡量。以3机9节点系统为例，设置3种不同的场景。场景1：三台同步机均投入运行；场景2：两台同步机组、一台可再生能源机组投入运行；场景3：一台同步机组、两台可再生能源机组投入运行。

本文根据图2的频率响应模型，系统在发生ΔPL的功率扰动后，系统频率响应 Δω表达式如下。

场 景1：

式中：G1（s）为同步机调速器和汽轮机模型的传递函数；G2（s）为系统惯量水平和阻尼特性的传递函数；G3（s）为新能源的惯量支撑和一次调频控制的传递函数。

在 不 同 场 景 下，G1（s），G2（s），G3（s）的 传 递 函数表示不同。3机系统在3种场景下的表达式如下所示。

场 景1：

若 为 阶 跃 扰 动，则 有 ΔPL（s）=a/s，a为 扰 动 的幅 值。带 入 式（3），（4）中，可 以 依 次 得 到 在 场 景1，和场景2，3的系统频率响应表达式，分别为

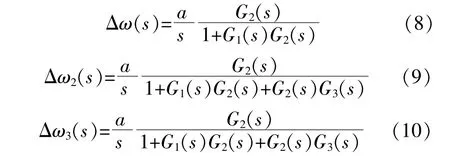
根据拉普拉斯变换终值定理，可求得系统稳态频率偏差的有名值为

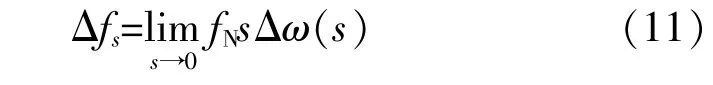
最大RoCoF幅值为

为计算最大频率偏差，对 Δω（s）进行拉普拉斯反变换，求导后可得：

式中：tp为第一个峰值频率的时间。

根 据 式（14）可 求 出tp，再 代 入 到fN·g（tp），即得频率最大偏差值。最大频率偏差、最大频率变化率幅值、稳态频率偏差是衡量系统调频能力的重要指标。稳态频率偏差和最大频率偏差越大，说明系统的抗扰能力越差。系统的最大RoCoF幅值过大会触及系统负荷减载。一些国家将最大频率变化率的幅值限制在0.125～0.5Hz/s，允许的最大频率偏差设定为0.2Hz[25]。本文选取最大频率偏差不大于0.2Hz，最大RoCoF幅值不大于0.5Hz/s。

2 频率响应定量分析

研究高比例新能源对系统频率变化动态过程的影响时，本文采用最大RoCoF幅值、最大频率偏差、稳态频率偏差3个指标来衡量。

2.1 不同控制方式下的频率响应指标

为研究不同控制方式下系统的频率稳定性，场景2，3具体设置如下。不考虑可再生能源机组惯量支撑和一次调频能力（h1=d1=0）的场景2，记为2-1；仅考虑新能源的惯量支撑能力 （h2=10）时，记为2-2；同时考虑新能源的惯量支撑和一次调频能力（h3=d3=10）时，记为2-3。不考虑新能源的惯量支撑和一次调频能力（h4=d4=0）的场景3，记为3-1；仅考虑新能源的惯量支撑能力（h5=10）时，记为3-2；同时考虑新能源的惯量支撑和一次调 频 能 力（h6=d6=10）时，记 为3-3。

3种场景的同步机参数相同，H=5s，R=0.05，ΔPL=0.025。在不同控制方式下，观察功率扰动后系统的频率特性，如图3所示。

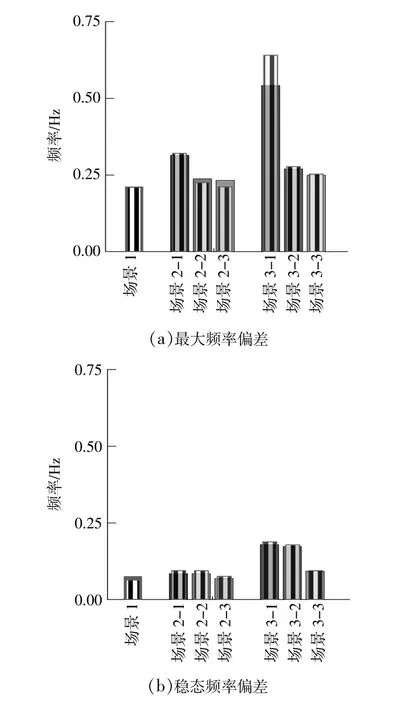
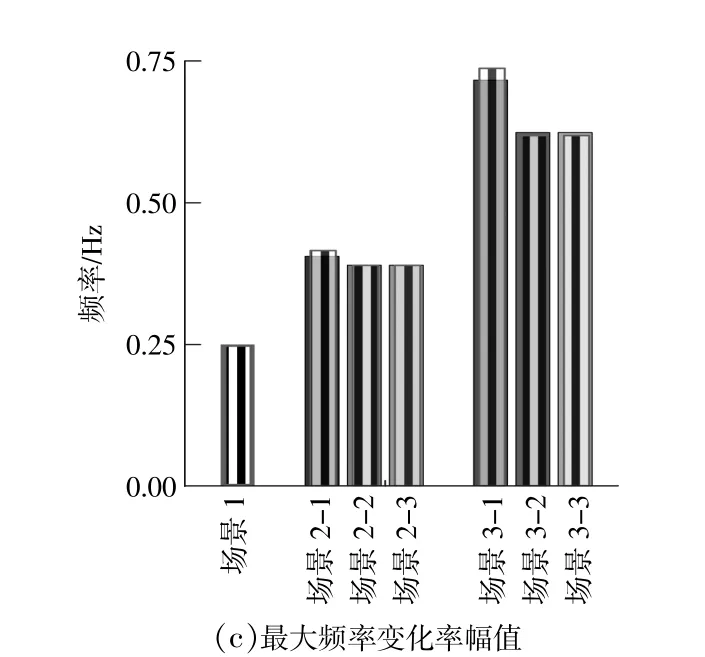
图3 不同场景下的频率响应指标柱状图Fig.3 Histogram of frequency response index in different scenarios（The gray shadow represents the calculation results of the model，and other colors are the simulation results）

由图3可知：①随着渗透率的提高，最大频率偏差和稳态频率偏差变大、最大RoCoF幅值增大。场景2的3个场景相较于场景1的最大频率偏差分别增大了50%，5.3%，-1.2%，稳态频率偏差分别增大了50%，49.7%，20.1%，最大RoCoF幅值分别增大了69%，58.4%，58.4%。场景3的3个场景相较于场景1的最大频率偏差分别增大了2倍、29.7%、18.2%，稳态频率偏差分别增大了2倍、1.8倍、49.7%，最大RoCoF幅值分别增大了2倍、1.5倍、1.5倍。根据计算结果，场景2-3的最大频率偏差比场景1的值都低，仅改变h和d的大小，对最大RoCoF幅值的影响最大；②考虑了新能源的惯量支撑的场景，最大RoCoF幅值相对减小：场景2-2相较于场景2-1减小6%，场景3-2相较于场景3-1减小16%。同时考虑新能源的惯量支撑和一次调频能力的场景受到扰动后的频率响应情形得到更大的改善，场景2-3的系统最大频率偏差比场景2-1的减小了34.2%，场景3-3的系统最大频率偏差比场景3-1的减小了60.6%。通过比较可发现，在渗透率高的场景3系统频率提升的效果更明显；③考虑最大频率偏差不超过0.2Hz、最大RoCoF幅值不超过0.5Hz/s的约束，场景1、场景2-2、2-3满足条件。而场景3-2，3-3的最大频率偏差在0.25Hz附近；④场景3-1的最大频率偏差通过两种方式得到的值差别明显。频率响应模型比时域仿真得到的最大频率偏差大18.1%。而考虑了新能源频率调节控制后得到的结果差别相对较小。

2.2 不同参数下的频率响应指标

为了量化有功功率扰动、新能源的惯性时间常数h和一次调频控制系数d对不同渗透率下电力系统频率响应的影响，让三者其一变化，分别计算不同参数在不同场景下的指标值，可以更加直观地分析出频率稳定特性。其中，功率不平衡扰动的 取 值[0.01，0.02，0.03，0.04，0.05，0.06]，新 能 源惯 性 时 间 常 数 的 取 值[0，5，10，15，18，20]，新 能 源一 次 调 频 系 数 的 取 值[0，5，10，15，18，20]。当 分 析不同功率扰动影响时，新能源惯性时间常数h和一次调频系数d均为10；当分析h变化的影响时，功率扰动设置为0.025且d=10；当分析d变化的影响时，功率扰动设置为0.025且h=10，如图4所示。虚线表示由频率响应模型计算得到的结果，实线表示仿真结果。

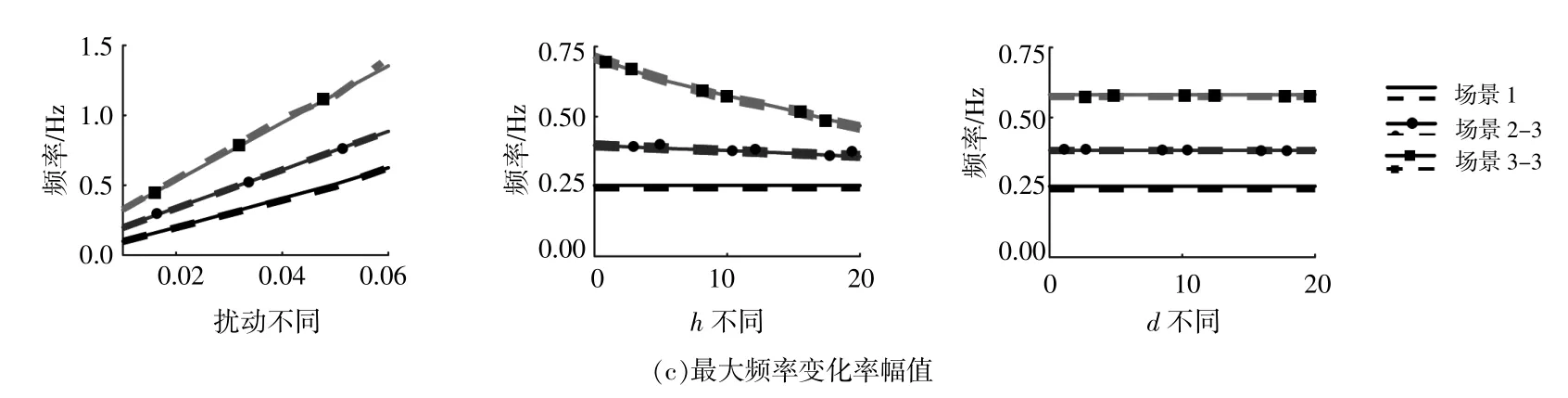
图4 不同场景下的频率响应指标折线图Fig.4 Line chart of frequency response index in different scenes

由图4可知，最大频率偏差与功率扰动、h和d均有关。最大频率偏差与功率扰动呈正相关，与h，d呈负相关。其中最大频率偏差随着d的增大而下降的趋势慢。稳态频率偏差与功率扰动和d有关。稳态频率偏差与功率扰动呈正相关，与d呈负相关，与h无关。最大RoCoF幅值与功率扰动和h有关。最大RoCoF幅值与功率扰动呈正相关，与h呈负相关。高渗透率场景下稳态频率偏差和最大RoCoF幅值两个指标值比低渗透率场景的大。其中，d=20时，场景1，2，3的稳态频率偏差相同。扰动不同时，渗透率高的场景下最大频率偏差值比低渗透率场景的数值微大。但是，当h约为15时，场景2，3的最大频率偏差比场景1的低；d约为5时，场景2的最大频率偏差比场景1的低。

3 仿真分析

3.1 仿真建模

在DigSILIENT/PowerFactory15.1中搭建含光伏的3机9节点系统模型[26]，如图5所示。

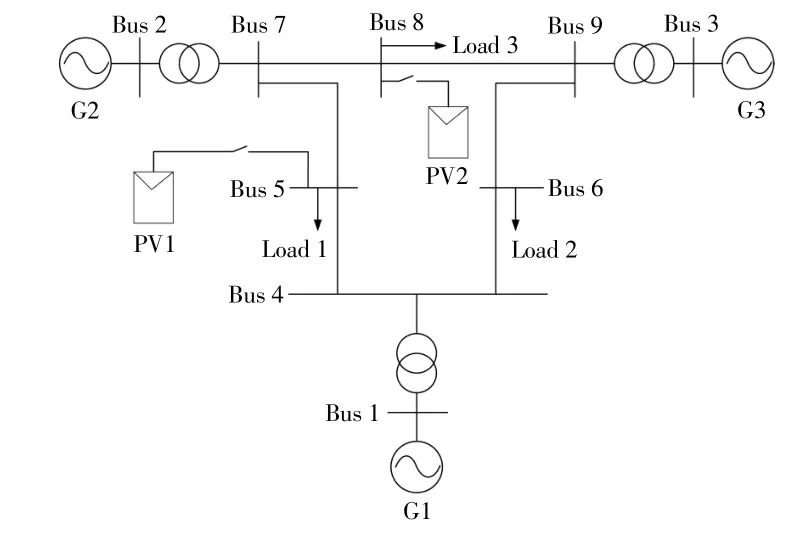
图5 3机9节点算例系统Fig.5 Three-machine nine-node test system

图中G1，G2，G3为再热式汽轮机的同步发电机组[19]，采用IEEE_DC1励磁控制型，调速器模型见图2。同步机的额定容量均为200MV·A，惯性时间常数为5s，调差系数均为0.05。包含两个光伏机组PV1和PV2，光伏发电系统等值机的参数见表1。调频控制相关的标幺值参数如表2所示。容量基准值为200MV·A。光伏发电系统按10%的容量配置储能单元。负荷扰动位置设在母线8（Bus8）处。

表1 光伏发电系统等值机参数Table1 Parameters of equivalent machine for photovoltaic power generation system

表2 仿真参数Table2 Simulation parameters

设置3种不同的场景，分析不同新能源渗透率对系统频率响应的影响。3种场景的初始稳态运行数据如表3所示。场景1：G1，G2，G3均投入运行；场景2：G1，G2投入 运行，G3退 出运行，光伏机组1投入母线5运行；场景3：G1投入运行，G2，G3退出运行，光伏机组1投入母线5运行，光伏机组2投入母线8运行。

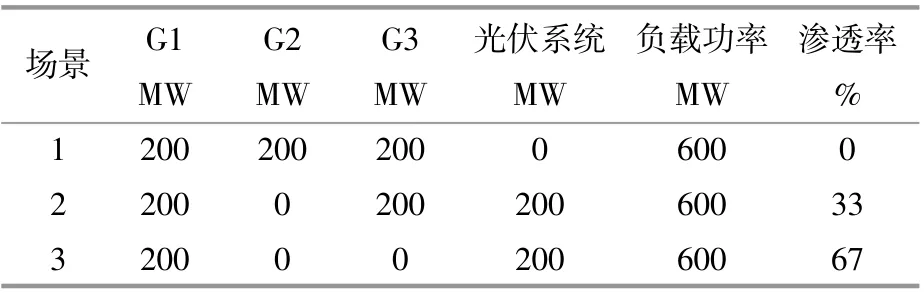
表3 3种场景的初始稳态运行数据Table3 Initial steady-state operation data of the three scenarios

3.2 仿真结果

不同参数时，系统的频率响应特性如图6～8所示。

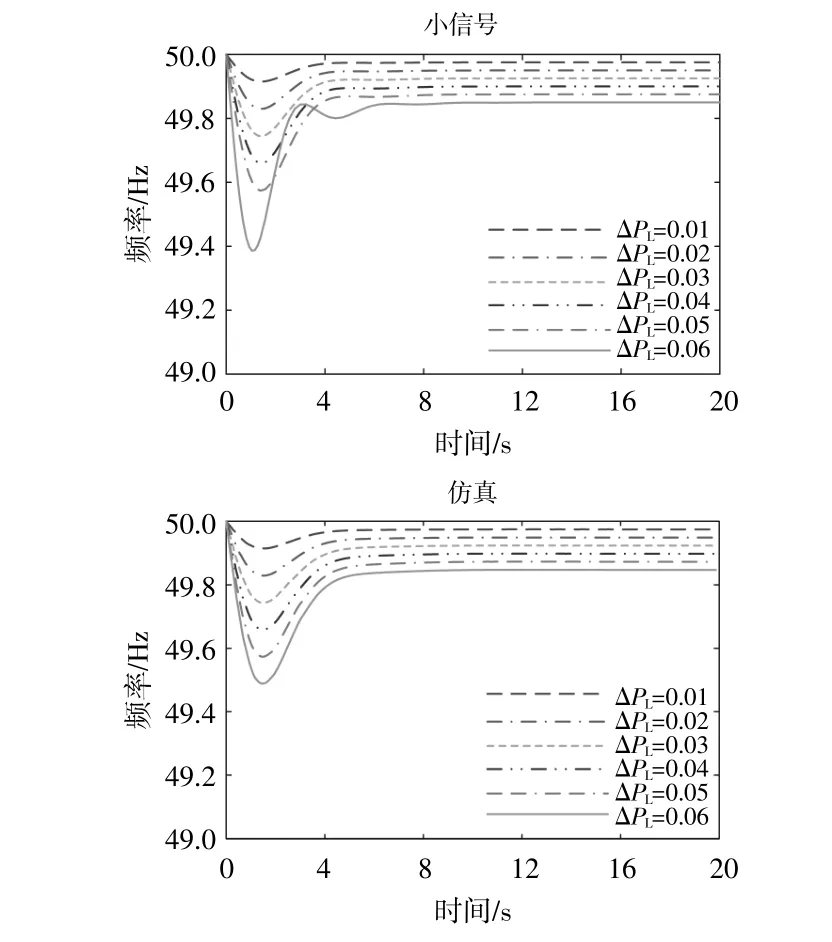
图6 场景1在不同负荷扰动下的频率响应Fig.6 The frequency response of scenario1under different load disturbances

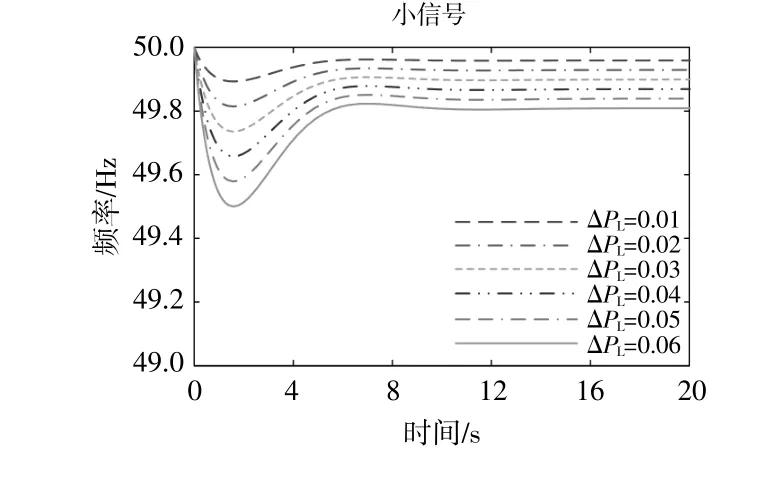
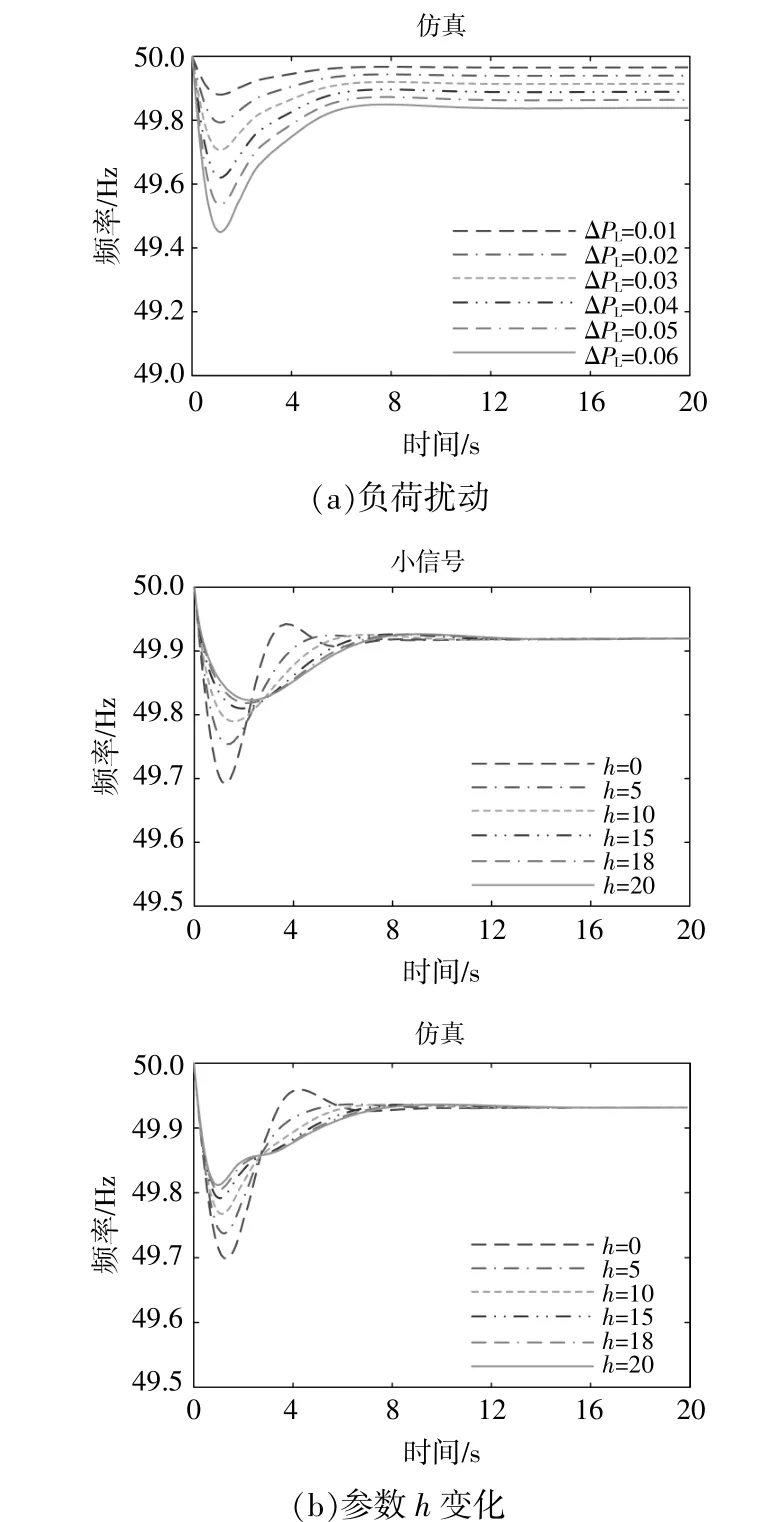
图7 场景2在不同参数下的频率响应Fig.7 The frequency response of scenario2under different parameters

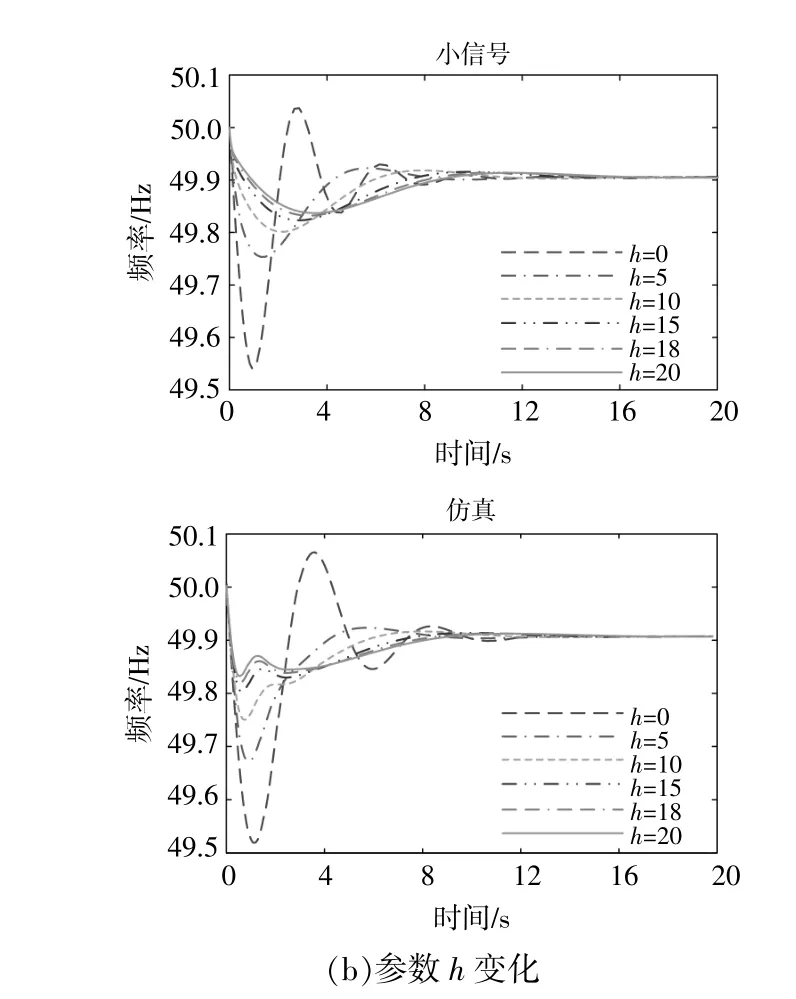
图8 场景3在不同参数下的频率响应Fig.8 The frequency response of scenario3under different parameters

图中，最大RoCoF的仿真值为扰动后250ms内，平均频率变化率结果与理论分析图4一致。因此，由图6～8可知：①系统受到的功率扰动增大时，最大频率偏差、稳态频率偏差、最大RoCoF幅值均呈上升趋势。其中，场景3最大RoCoF幅值的上升陡度更大，且与低渗透率的场景差距明显。当考虑最大RoCoF幅值约束时，3个场景能承受的功率扰动逐渐降低。场景1，2，3可承受的功率扰动依次是0.05，0.035，0.02。若考虑最大频率偏差不超过0.2Hz的限制，可以发现3个场景可允许承受的最大扰动在0.02附近。因此，在高渗透率下系统功率缺额过大时无法满足频率约束，且高比例场景下尤其需要提高可再生能源机组的惯量支撑能力；②随着h增大，场景2，3的最大频率偏差不断减小。当0＜h＜5时，场景3的最大频率偏差比场景2下降的速度更快。与理论计算结果相比，场景3最大频率偏差的仿真值随着h增大而下降的趋势慢。当h=12时，场景2，3的最大频率偏差值低于场景1。当h≥15时，可以保证高渗透率系统的最大频率偏差满足0.2Hz的约束。稳态频率偏差会随着渗透率的提高而增大，这是由于3个场景的调差系数取值不同。在场景3情况下,最大RoCoF幅值有明显下降趋势，但其值只有在h≥15时才满足最大RoCoF限值；而场景1，2的最大RoCoF幅值始终小于约束值。因此，当h≥15时，高渗透率下的最大频率偏差和最大RoCoF幅值均满足约束条件；③当d增大时，系统的稳态频率偏差会降低，当d取值为20时，场景1，2和3的稳态频率偏差值会重合，此时3个场景具有相同的一次调频能力。最大RoCoF幅值几乎不随d变化而变化，且场景2的最大RoCoF幅值始终不超过限值，约为0.38Hz/s，而在渗透率高的场景3下最大RoCoF幅值约为0.59Hz/s。当d＞5时，场景3的最大频率偏差变化趋势不明显，约为0.25 Hz，高于场景2的最大频率偏差值。

4 结论

本文基于同步发电机的经典传递函数模型，考虑可再生能源参与惯量支撑和一次调频控制，建立了算例系统的频率响应模型，并通过最大频率偏差、稳态频率偏差、最大RoCoF幅值3个指标来量化参数变化时，不同渗透率场景下的频率响应特性。不同渗透率场景下的理论计算与仿真结果表明：①尽管RoCoF指标在不同渗透率场景下的数值均大于全同步机系统，在惯性时间常数较大时，高渗透率场景下的最大频率偏差指标优于全同步机系统；②在低渗透率场景下，RoCoF指标始终满足要求，应重点关注最大频率偏差指标。在满足最大频率偏差指标限制的前提下，为节约调频成本，可再生能源机组的惯性时间常数和一次调频系数可以取较小值；③在高渗透率场景下，当惯性时间常数和一次调频系数取值均较大时，能够同时满足最大频率偏差和RoCoF指标的约束。为了进一步降低最大RoCoF幅值，除增大惯性时间常数以外，还应加快可再生能源机组的惯量功率响应速度。