运力受扰下的物流无人机干扰恢复模型

任新惠， 苟利珍， 武彤

(1.中国民航大学经济与管理学院， 天津 300300； 2.中国民航大学交通科学与工程学院， 天津 300300)

最后一公里配送被认为是物流链中效率最低、污染最为严重的环节，为了实现绿色包裹交付，用无人机代替卡车运输，除了无人机电池充电外，很少涉及碳足迹，从运输时间、运输成本、碳排放进行分析，无人机相对于卡车运输具有显著优势[1]，国内学者针对农村物流配送场景，考虑无人机飞行能力、最大载重能力等规划无人机调度路线[2],并结合当前疫情防控的大背景，提出无人机和车辆联合配送模式，与区域限制相结合，解决配送效率问题[3]。国外学者将无人机应用于即时交付场景，考虑与有效载荷有关的飞行能耗，得到更贴合实际的任务分配方案[4]，同时设计相关算法，进一步优化配送成本问题[5]。但随着无人机的广泛应用，运行事故不断增加。这些事件的显著特点是发生时间的随机性，发生位置的不确定性、影响程度的差异性和解决方案的特殊性。如何快速有效地对初始方案进行调整，生成对原始配送系统扰动最小的新方案，同时协调各方利益，这是无人机实际应用中迫切需要解决的问题。

目前关于无人机飞行干扰研究，部分学者从无人机自身运行安全出发，进行风险分析和评估[6]，规划最优航路[7-8]，运行故障概率分析[9]。也有学者关注无人机飞行阶段的交付可靠性问题，通过考虑飞行故障概率来描述包裹交付的不确定性[10-13]。这些研究主要集中于事前决策，关于无人机干扰事件发生后的实时决策研究较少，而车辆物流中干扰管理理论为解决无人机干扰后的实时决策提供了理论依据。物流干扰管理不是全局重新规划，而是以当前计划为基础快速生成对系统扰动最小的方案。国内学者王旭坪等[14]针对车辆配送途中发生故障，不能继续完成配送任务的情况，提出3种扰动恢复策略。王清斌等[15]针对新增运输任务情况，以最小广义费用偏离目标验证干扰管理方法的有效性。丁秋雷等[16]针对配送时间延迟场景，考虑客户感知因素，将客户终身价值、配送成本等作为扰动度量函数，确定干扰后的客户交付顺序、交付位置、交付时间等决策参数。国外学者Wu等[17]针对易腐货物的干扰交付问题，考虑货物易腐性、交通流的时间依赖性，交通网络的备选路径，建立基于分批交付的干扰恢复模型。Tao等[18]基于同时取送货的车辆路径问题，从配送成本和时间窗偏差两方面进行扰动度量，引入目标逐级优化的思想，建立基于客户需求变化的两阶段干扰管理模型。

现有研究致力于无人机正常运行条件下的配送调度问题，对于其交付可靠性的重视程度不高，大部分没有考虑服务中断情况，都假设能够实现完美交付，这一情况是不符合实际的。在运输过程中，不确定时刻下的运力变化，需求时间窗、需求位置、需求量变化将使得问题变得复杂，一旦发生事故后不能快速提供一个有效的解决方案，客户对于配送风险会表现出厌恶心理，物流配送企业将会受到重大的打击，物流动态干扰下的调度恢复是末端配送所要解决的重点问题。当前的无人机技术和应用仍处于不断发展阶段，技术的不成熟和政策的不完善决定了事故风险概率，这是未来无人机发展面临的挑战，鉴于在动态环境下的无人机飞行系统易受到突发事件、机身故障和极端天气等影响，使得初始调度方案的执行变得困难，因此干扰事件发生前预先考虑无人机飞行故障概率、阶段能耗，优先服务高价值、高需求的客户订单，减少向客户交付失败的需求损失，同时考虑配送成本，建立预调度模型；而实际干扰发生后，将干扰管理理论与无人机配送结合，充分考虑运行环境中不确定因素，以偏差时间和扰动成本最小为目标，建立干扰恢复模型，采用蚁群算法快速生成扰动最小的应对方案，实现静态动态模型相结合，事前和事后决策相结合，弥补单一静态模型与实际运行情况存在不符情况的不足。

1 问题描述及假设

1.1 无人机服务模式及问题描述

无人机服务被描述为无人机的交付功能，根据末端客户的服务时间、物流服务商的金钱成本和不确定环境影响，利用相关方法匹配出最优的交付方案，完成包裹从起始端运输到末端的交付任务，包括初始计划的制定、干扰路线的调整、交付功能。无人机末端服务模式如图1所示，针对末端物流配送时车辆不方便或无法进行配送的场景，采用小型无人机来完成物流包裹的配送工作。物流服务商收到需求点的配送要求，从配送中心安排一定数量的无人机运输货物，无人机垂直起飞降落，依次完成任务，最后空载回到配送中心。

图1 无人机服务模式Fig.1 UAV service mode

制定无人机交付计划，需要满足无人机载重量、载容量、电池能耗、客户时间窗等限制，每个任务点在时间窗条件限制下只访问一次。考虑到无人机在飞行过程中受到多种不确定性因素，可能造成故障坠落、故障备降、故障延误等情况，使得订单需求损失增大、客户满意度降低。针对故障坠落场景，当无人机配送任务执行到T0时刻，有一架或多架无人机发生故障坠落，失去运力，同时认为所载货物已经发生损坏，直接导致调度任务中断不能按照原始配送方案执行，此时需要快速及时地生成新的解决方案，并使其与原始配送方案的偏离程度最小。

1.2 问题假设

(1)所有无人机都在同一配送中心出发，完成送货后返回原配送中心。

(2)无人机开始配送任务时电量已经充满，不考虑中途的充电问题。

(3)无人机的飞行速度已知，且保持匀速飞行。

(4)每个客户只能被一架无人机服务。

(5)无人机发生故障坠落，造成货物损坏，货物不同质，只能重新调度新无人机。

(6)如果货物没有在客户要求的时间窗内达到，将取消订单。

1.3 变量说明

根据相关问题描述进行变量定义说明如表1所示。

表1 模型参数设置Table 1 Parameter setting of model

2 物流无人机干扰恢复模型构建

2.1 不确定飞行故障下的无人机预调度模型

无人机在正常运行情况下，以交付成本最小作为优化目标，并根据客户需求、电池、无人机自身特性进行模型约束。实际运行过程中，可能遭遇来自系统故障、气象环境、人为操纵等干扰，导致包裹不能在指定时间内送至目的地，造成需求损失，因此，在原始交付模型中，增加无人机飞行故障概率[9]，优先为高价值、高需求客户提供服务，减少预期需求损失。假设无人机运行中发生故障的概率为p，不发生故障的概率q=1-p，无人机k服务第i个客户途中发生故障的概率为Fik，发生故障后对应剩余货物价值为Di。

Fik=pq(i-1)

(1)

(2)

(3)

(4)

(5)

(6)

(7)

(8)

式(3)为无人机不确定故障条件下对应的最小需求损失；式(4)为无人机的固定成本；式(5)为无人机在全部需求点的服务成本；式(6)为无人机在全部需求点的等待成本；式(7)和式(8)分别为无人机运载成本和空载成本。

针对客户订单，同时考虑有效载重量和飞行时间2个因素。认为载重量越大、运输时间越长，消耗电池的能耗总成本就越高，借鉴Dorling等[19]推导的线性能耗模型，即

(9)

式(9)中：a为运载1 kg的电池和订单需要的功率；b为没有有效载荷重量或电池重量时，无人机保持悬停状态所需要的功率。

根据上述目标函数描述，建立模型如下。

min(Z1+Z2+Z3+Z4+Z5+Z6)

(10)

(11)

(12)

uij-uje=wj, ∀i,e∈N0,∀j∈N,i≠j,j≠e

(13)

xijk+xjik≤1, ∀i,j∈N,i≠j,∀k∈M

(14)

(15)

(16)

∀k∈M,i≠j

(17)

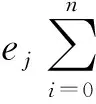
∀k∈M

(18)

式(10)是广义总费用最小；式(11)保证每个需求点只有一架无人机服务；式(12)保证无人机从配送中心出发，服务完最后一个需求点后返回配送中心；式(13)为无人机飞行到任意阶段对应有效载重量和需求点订单重量之间的关系；式(14)消除子回路，任意两个需求点之间最多只有一条路径；式(15)、式(16)分别为无人机最大载重、载容限制；式(17)为无人机飞行最大能耗限制；式(18)为任意需求点的时间窗要求。

2.2 无人机干扰坠落后的恢复模型

针对包裹配送过程中无人机坠落场景，从客户服务和配送成本2个角度进行扰动度量，建立干扰恢复模型为

min Lex:

(19)

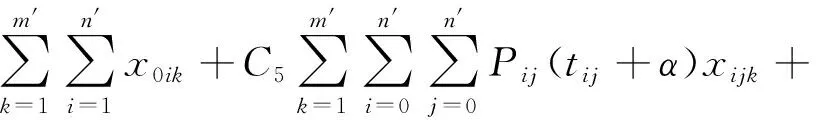
(20)

(21)

(22)

ej-Δtj≤S′jk≤lj+Δtj, ∀j∈N′

(23)

waitik+t′ik=S′ik, ∀i∈N′,∀k∈M′

(24)

T0+t0j+α+waitjk-D(1-x0jk)≤S′jk,

∀j∈N′,∀k∈M′

(25)

S′ik+tij+si+α+waitjk-D(1-xijk)≤S′jk,

∀i,j∈N′, ∀k∈M′

(26)

式(19)、式(20)为目标函数，式(19)表示原始方案和新方案中顾客的开始服务时间偏差最小，且尽可能使所有顾客都能得到服务，同时采用客户分级策略区分不同客户的影响程度，客户的重要程度用该客户的货物价值占配送货物总价值的比重表示；式(20)表示物流服务商的成本扰动，考虑新增无人机的固定成本、能耗成本、取消客户惩罚成本；式(21)表示未受干扰影响的需求点仍由原始无人机执行配送任务；式(22)表示受干扰的每个需求点访问一次，或者采取取消策略不访问该需求点；式(23)表示干扰发生后，很难在期望时间窗范围内完成配送，新增时间容忍度，形成新的时间窗要求；式(24)、式(25)、式(26)表示时间变量关系。

2.3 改进蚁群算法设计

所构建的基于带时间窗订单的无人机调度模型属于NP优化问题，设计蚁群算法进行求解，根据无人机飞行中能量损耗和货物损失量的不同，在算法中加入分段能耗计算方法；考虑到基本蚁群算法的转移概率公式包含特征信息较少，导致算法搜索能力不足，收敛速度慢，将客户需求时间窗和达到等待时间加入状态转移公式当中。同时为了避免算法陷入局部最优解和随机解，对挥发因子ρ进行动态调整。

步骤1解决无人机在正常运行条件下的配送问题，最小化配送成本，利用蚁群算法得出原始最佳配送方案。

步骤2当无人机干扰发生时刻，受扰无人机尚未服务的客户是受扰客户，其余正常运行无人机的客户不受干扰，按原始计划继续配送。对于受扰客户采用取消策略和新增无人机策略进行服务，首先需要判断受扰客户是否取消服务。客户i的需求服务时间窗[ei+Δti，li+Δti],开始服务时间S′ik,当S′ik>li+Δti，取消客户订单，转步骤3。

步骤3针对受扰需服务的客户，以客户服务偏移扰动和成本扰动最小为目标函数，使用步骤1中的算法对未受扰客户重新规划配送方案。

步骤4进一步优化配送成本。在S′ikQ2，步骤3的配送方案为最优方案。算法流程如图2所示。

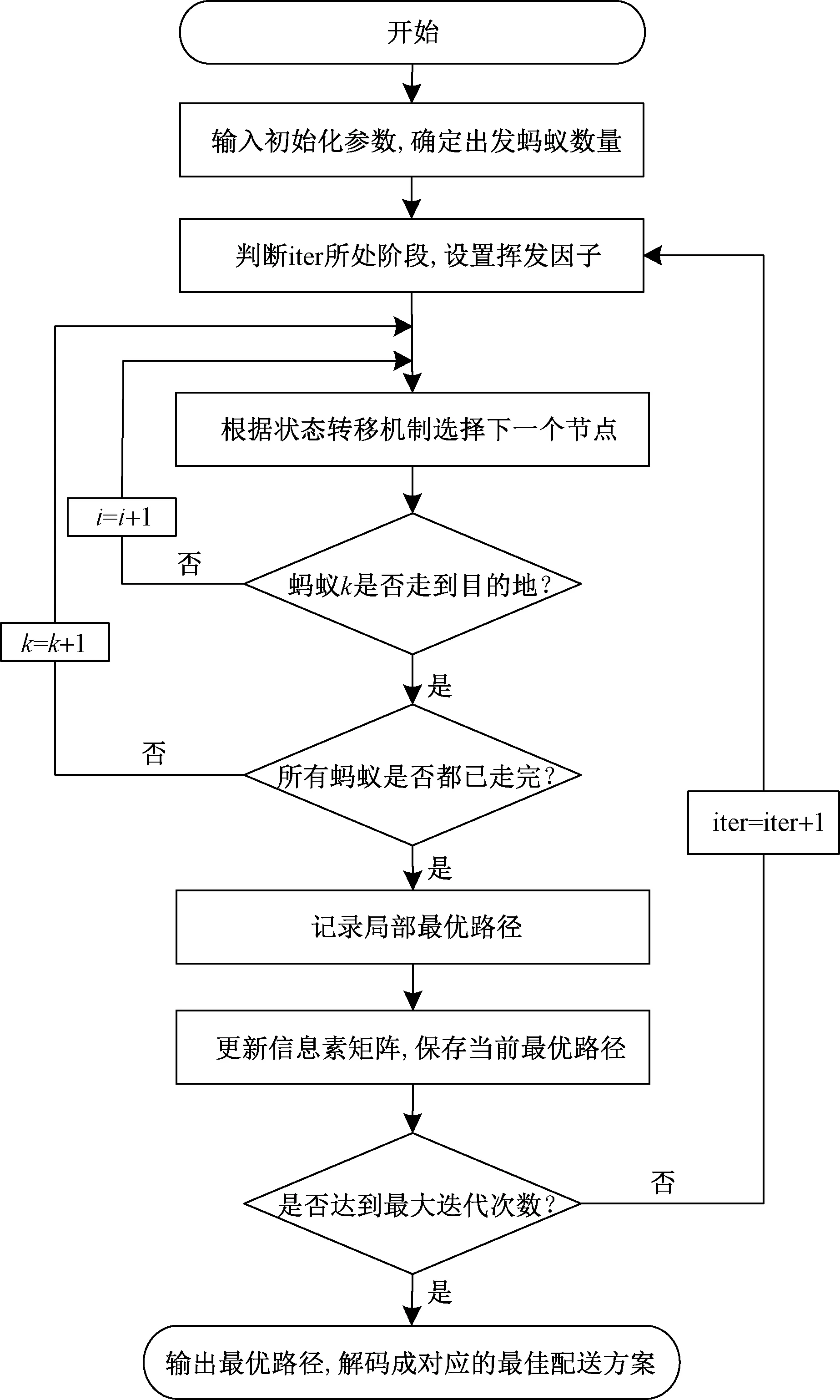
图2 蚁群算法流程图Fig.2 Flow chart of ant colony algorithm

为了验证算法的收敛性，使用标准Solomon数据库的中r201数据，利用MATLAB R2019b进行编程，实验环境为处理器Intel(R) Core(TM) i5-8300H CPU @ 2.30GHz,内存8 GB，Window10操作系统，设置迭代次数为100，种群规模为100，算法收敛情况对比如图3所示。

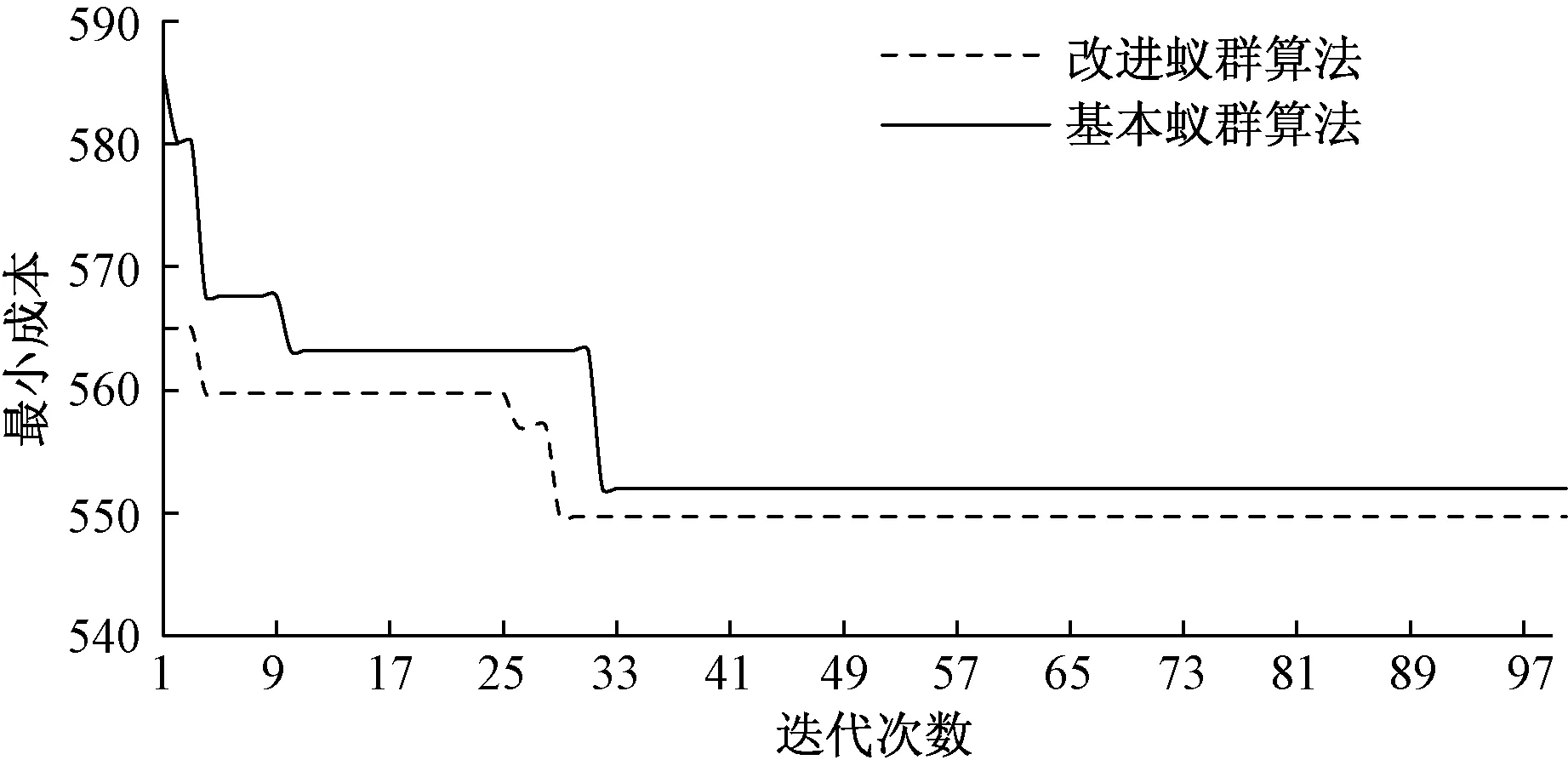
图3 算法收敛情况对比Fig.3 Algorithm convergence comparison

由图3结果可知，改进蚁群算法有更好的收敛性，收敛时间会随着问题规模的增大而增大，时间复杂度增大，但随着蚂蚁数的增加，收敛时间逐渐减小，即时间复杂度减小。

3 数值实验及结果分析

参考Solomon关于VRPTW的经典基准算例对上述模型的有效性进行验证。该算例中没有涉及货物的体积、货物的价值，在运算中这部分数据随机生成，考虑到无人机和车辆运输的相关参数性能不同，需求时间窗和货物重量做相应调整。参考杭州迅蚁公司的旋翼物流无人机性能参数，设置最大载重5单位，最大载容64单位，最大飞行能量1 800单位，成本参数C1=15、C2=0.1、C3=0.1、C4=0.1、C5=0.05。

以数据r201的25个客户为例，根据预调度模型得出初始最优配送方案，无人机1：0→1→7→18→12→0；无人机2：0→19→8→10；无人机3：0→11→9→20→0；无人机4：0→23→22→24→0；无人机5：0→16→17→13→0；无人机6：0→6→2→25→3→0；无人机7：0→5→14→15→0；无人机8：0→4→21→0。为了验证不确定干扰对配送方案结果的影响，设置对照实验，服务偏移扰动目标和扰动成本目标随权重变化的结果如图4所示。

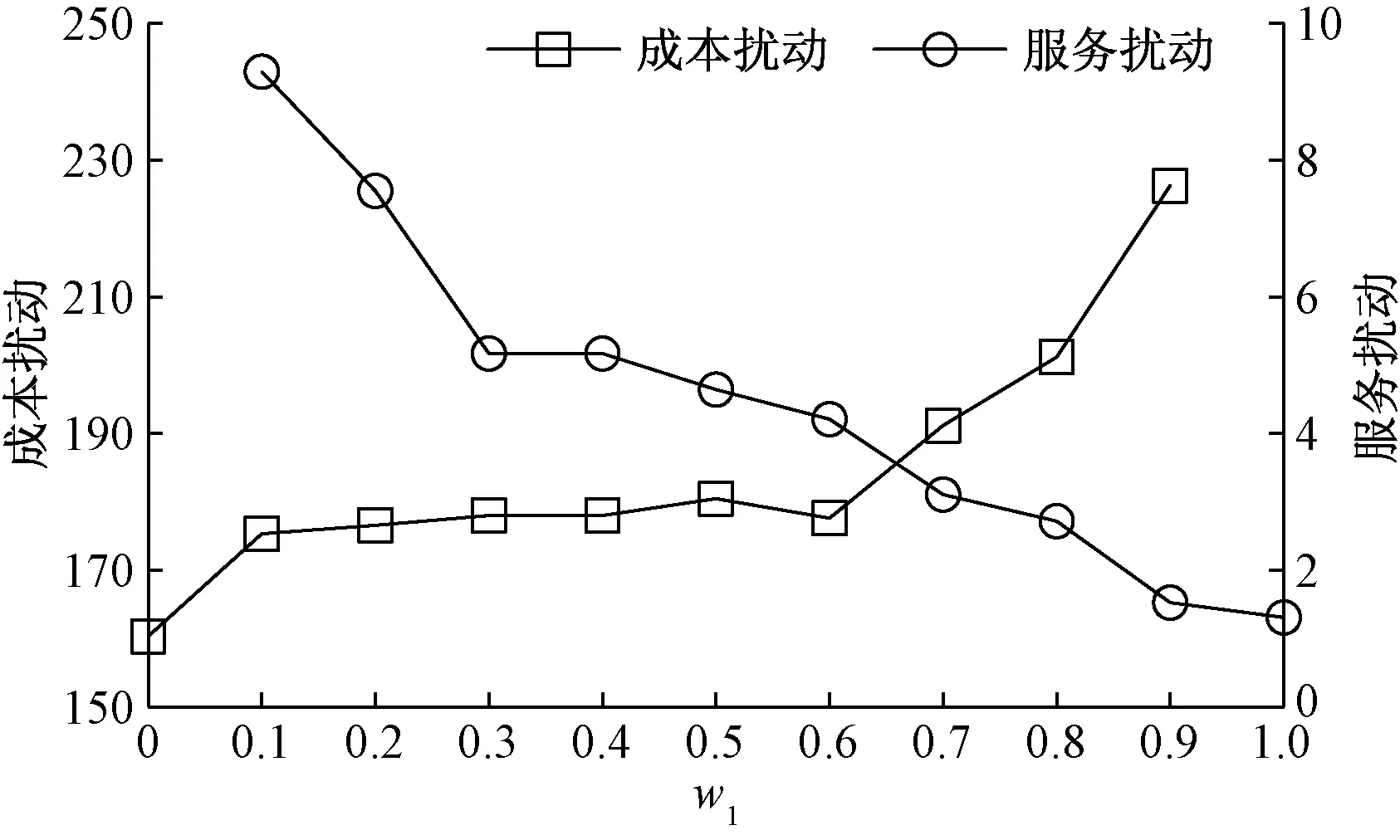
图4 目标函数随权重变化曲线图Fig.4 Change curve of objective function values with weights

由图4可知，随着服务偏移扰动目标权重w1的逐渐增大，配送结果的服务偏移呈现波动递减趋势，同时配送成本呈现波动递增的趋势，实验结果显示，w1=0.6的配送方案表现结果最好，选取权重比：服务扰动权重w1=0.6,成本扰动权重w2=0.4。

为了验证干扰恢复方案的有效性，随机选取3组受扰情境。干扰情境1：无人机6在服务第一个客户途中；干扰情境2：无人机6已服务完第二个顾客，正前往第三个顾客途中；干扰情境3：无人机1和无人机6在前往第一个客户途中；在上述干扰场景下将本文干扰恢复方案结果与原始配送方案比较，如表2所示。

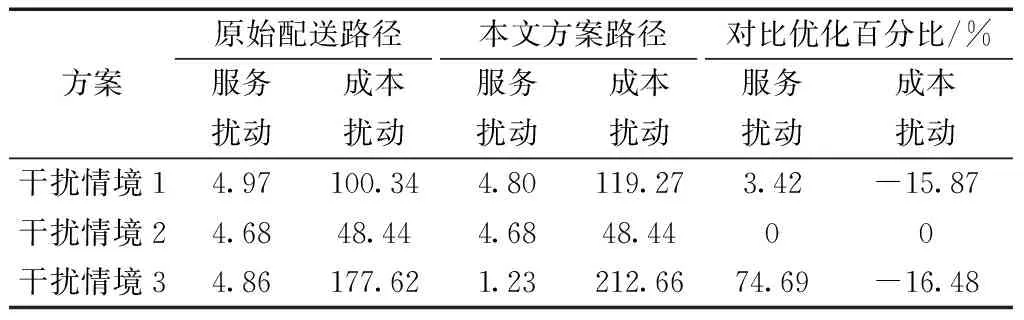
表2 结果比较Table 2 Comparison of results

(1)干扰情境1。原始配送路径0→6→2→25→3→0；新救援路径0→6→3→0，0→2→25→0；由于无人机发生干扰坠落时间较早，能在时间窗内完成配送服务，因此没有取消的客户，新方案使用了两架无人机进行服务，配送成本增加了15.87%，客户服务满意度提高了3.42%，由于新增无人机服务的客户数较少，成本代价较大。

(2)干扰情境2。受扰客户25和3，原始配送路径和新救援路径为0→25→0。干扰发生时刻较晚，重新调度无人机不能在客户3的时间窗完成配送服务，最终取消该客户，而直接新派无人机服务客户25。

(3)干扰情境3。原始配送路径0→1→7→18→12→0，0→6→2→25→3→0；新救援路径0→7→18→3→0，0→12→25→0，0→6→1→2→0。干扰发生时刻较早，同时受扰客户数量较多，新方案中的调整空间较大，以成本增加16.48%的代价使得客户的服务时间偏移值减少74.69%。

由上面干扰调度发现干扰发生位置不同，受扰时刻越晚，允许调整的时间越少；受扰客户数越少，满足约束的调整方案也越少，很难有明显的优化效果，所以本文方法针对多受扰客户、早干扰时刻场景的适应性更好。针对干扰后的客户，增派新无人机按照新的配送方案服务，更好地权衡成本和客户服务，从长远利益考虑，短期的成本代价换取客户的长期信赖，能获得更大的价值。

4 结论

无人机执行配送任务过程是处在一个高动态、高复杂的不确定低空环境当中，这些多种不确定因素可能会导致物流无人机的配送任务中断。研究中断后的恢复方案，得到以下结论。

(1)综合考虑无人机垂直起降时间、飞行阶段能耗、最大载重载容量、需求时间窗、货物价值等多因素约束；基于不确定故障下构建无人机配送预调度模型，减少了需求损失。

(2)建立的恢复模型可以在控制支出成本下，维护客户的服务满意度，当干扰发生时刻早、受扰客户多时，仅以16.48%的成本代价，使得客户满意度提高74.69%，同时快速生成干扰后的应对方案，有效提高物流无人机运输系统的干扰处理能力。

(3)根据干扰对无人机机身造成的破坏强度、货物完好性、持续时间的不同，将无人机飞行能力受到干扰情况细分了3种场景：坠落货损、故障备降、干扰延误。此次以坠落货损场景展开研究，今后将进一步完善无人机多受扰场景下的调度决策。