火箭下投式探空温度传感器设计

汤鸿霄， 刘清惓*， 杨杰， 段然， 葛祥建， 恽雨涵

(1.南京信息工程大学江苏省大气环境与装备技术协同创新中心， 南京 210044; 2.南京信息工程大学江苏省气象探测与信息处理重点实验室， 南京 210044； 3.南京信息工程大学电子与信息工程学院， 南京 210044)

近年来，随着对气候变化以及超高空大气环境的研究不断深入，国内外学者针对平流层以上的大气环境展开了大量研究[1-4]。Erell等[2]的研究证明了在高空中太阳辐射误差随着太阳辐射强度的增加而增加，随着气流速度的增大而减小。丁枫[3]的研究采用阵列式球形温度传感器测量10～30 km的大气环境以获得0.16 K的平均辐射误差。刘洋等[4]用热电偶作为探空仪的测温工具也可使辐射误差减小。

但上诉研究的探空仪皆采用探空气球搭载，其有飞行高度限制，往往气球上升到30 km以上的高度就会发生爆裂，所以传统探空仪几乎无法测量超过这一高度的大气环境。但是，随着科技水平的进步，30～80 km高空大气环境探测变得同样不可忽视，不仅能对气象预测产生帮助，还能对中国未来将会投入使用的超高速飞行器的飞行环境进行先行研究。故现采用火箭下投式探空仪，并使用阵列式热电偶作为测温元件，对传统探空仪无法到达的高空大气环境进行探测研究。

火箭下投式探空温度传感器由火箭搭载升空，并于距地面80 km左右的高度下投，探空仪配备降落伞系统来缓解一定的下落速度，并于下落过程中持续、快速地采集高空中的各种气象数据。

在超高空中，太阳辐射误差是导致温度测量不准确的主要原因，其是由热辐射与热传导在温度传感器上的双重作用而造成的[1]。在30～80 km的高空，空气稀薄、太阳辐射更强，所以设计的重点是如何在超高空中更为恶劣的大气环境中尽可能地减小太阳辐射误差，因此现提出一种热电偶阵列温度传感器设计。首先使用Pro/E建立探空仪的整体模型，再通过Fluent仿真软件得出不同尺寸的热电偶探头太阳辐射误差最小者，接着用计算流体动力学(computational fluid dynamics，CFD)方法计算出表面涂覆不同太阳辐射吸收率材料的热电偶探头相互的辐射误差比值。并采用支持向量机(support vector machine，SVM)算法拟合处理数据。最后以低气压风洞与太阳模拟器作为实验平台，验证火箭下投式温度传感器的准确性与可靠性。

1 火箭下投式传感器的模型与原理

1.1 传感器物理模型

针对超高空大气环境并结合火箭探空仪的设计所需，提出了一种以热电偶阵列作为温度传感器的探空仪系统设计方案，其结构示意图如图1所示。

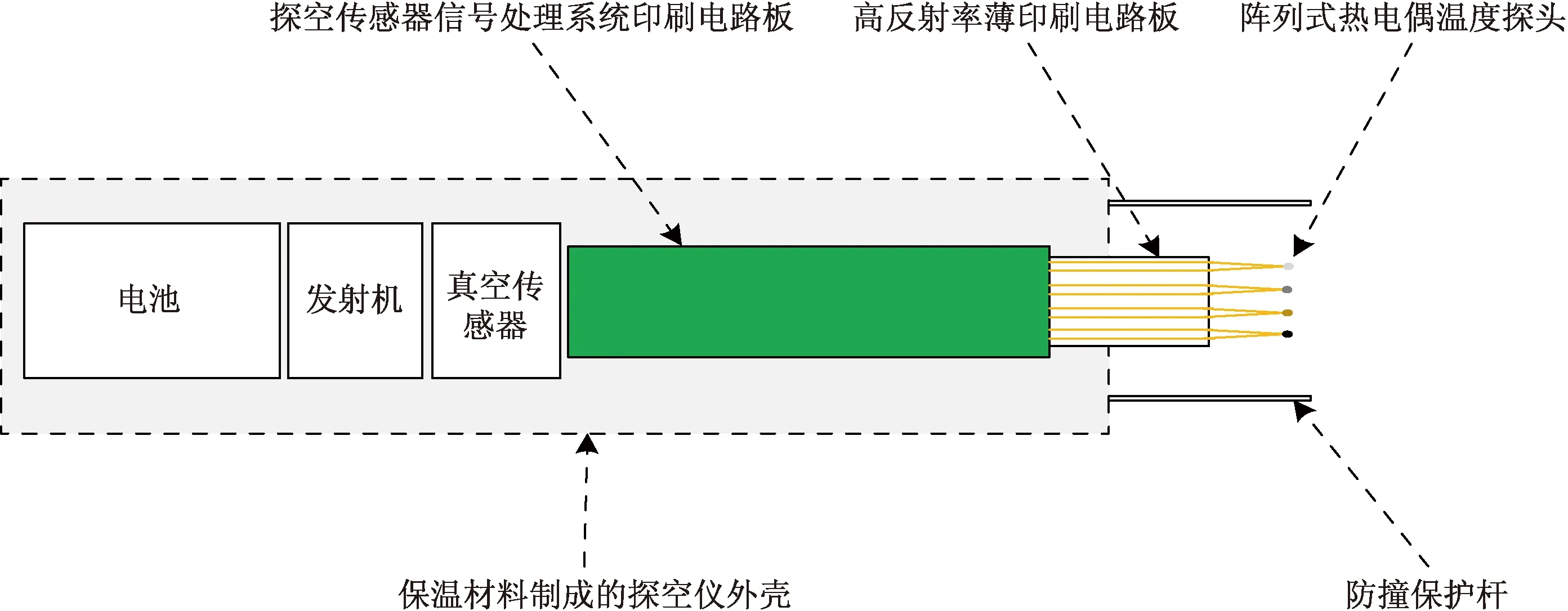
图1 火箭下投式探空仪结构示意图Fig.1 Structure diagram of rocket drop radiosonde

在一些地面气象探测中采用的太阳光挡板，不适用于火箭探空仪，因为挡板体积大、散热差、热惰性大，会强烈地吸收太阳辐射，并产生显著升温，对温度测量造成干扰。此外，在探空仪剧烈摆动过程中，挡板会形成显著的热尾流，并容易对传感器探头形成热污染。因此，将微型温度传感器探头置于探空仪的最前端。为防止在运输、安装过程中，操作人员意外触碰探头造成损坏，在探空仪头部，设有2个保护杆，其形状为圆柱状，长度为60～80 mm，直径为2～3 mm。保护杆的表面材质为铝或银，内部材质为金属或塑料。探空仪整体模型如图2所示。

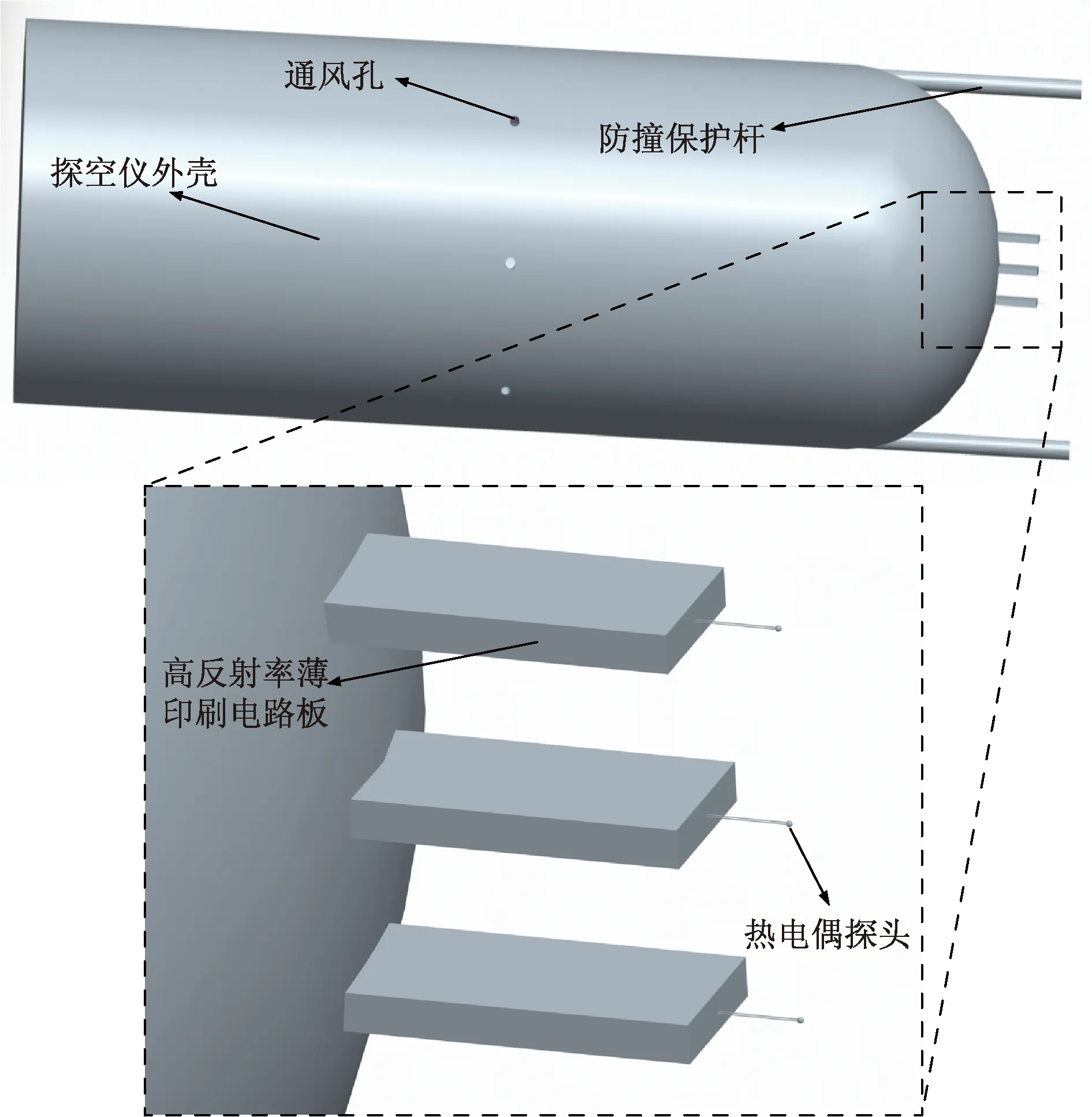
图2 探空仪整体模型Fig.2 Overall model of radiosonde

1.2 传感器工作原理

传感器由4个温度传感器探头组成，其有不同太阳辐射吸收率的涂层，构成了阵列式热电偶。4个探头分别涂覆了一层银、铝、铜与黑色涂层，使热端探头具有不同的太阳辐射吸收率。高空大气密度、太阳辐射强度、环境气体流速等环境因素以及探头表面不同的辐射吸收率的影响使每个探头的辐射误差不同。因此真实环境温度可由各个探头之间的辐射误差比值关系计算得出[3]，传感器结原理意图如图3所示。

图3 温度传感器原理示意图Fig.3 Schematic diagram of temperature sensor

传感器探头A表面涂覆了一层银质涂层，其太阳辐射反射率最高，经过一段时间的太阳光照后，探头A的辐射误差和真实温度值分别为ΔTa、Ta。传感器探头B表面涂覆了一层铝质涂层，其太阳辐射反射率次之，施加同样强度的太阳辐射后，探头B的辐射误差和真实温度值分别为ΔTb、Tb。传感器探头C表面涂覆了一层铜质涂层，其太阳辐射反射率再次之，施加太阳辐射后，探头C的辐射误差和真实温度值分别为ΔTc、Tc。传感器探头D表面的涂层与上述3种涂层相比，其太阳辐射反射率最低，施加太阳辐射后，探头D的辐射误差和真实温度值分别为ΔTd、Td。无辐射环境下，4个探头的温度测量值均为Tx。使用探头D测量值作为参照，用其他3种不同涂层的探头测量值与其相比，其间的辐射误差比值公式分别为

(1)

(2)

(3)

式中：H为海拔高度；V为环境气体流速。由此可推算出

(4)

(5)

(6)

可推算出大气温度的真实值Tx分别为

(7)

(8)

(9)

(10)

式中：Tx为真实环境温度最终值。探头A、B、C的辐射误差比值换算成环境温度值的公式分别为式(7)、式(8)与式(9)。

1.3 阵列式热电偶传感器探头设计

使用4个微型热电偶组成阵列，其热端探头为测温元件，并通过硅酮导热胶使探头与外层涂覆的不同反射率材料贴合。导热胶与外界连接处用防水胶，提高绝缘性能，避免雨水和湿气影响绝缘电阻。因铂电阻精度、稳定性高的特点[4]，热电偶的冷端补偿器件选用铂电阻Pt100[5]，4个热电偶共用同一冷端以减小测量时不必要的误差。将铂电阻和热电偶的冷端一起放置在导热胶中，保证两者温度的一致性，并在外层涂覆极低太阳辐射吸收率的银质反射层。利用这种设计方式，降低了冷端探头的整体太阳辐射误差，以达到提高测量精度的目的。热电偶阵列传感器的结构如图4所示。

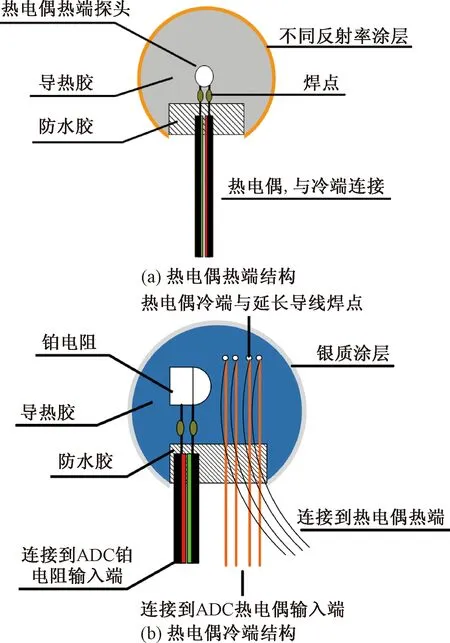
图4 阵列式热电偶结构示意图Fig.4 Structural diagram of array thermocouple

2 研究方法及仿真结果分析

2.1 研究方法

火箭下投式探空温度传感器的研究设计分别从传感器探头尺寸选择仿真、阵列式热电偶辐射误差比值仿真和实验3部分进行分析[6]。尺寸仿真部分先利用Pro/E建立不同尺寸的热电偶探头基本模型，接着在ICEM中定义材料点并进行网格划分，其次通过Fluent进行仿真计算，分别计算出不同尺寸探头在不同高度、不同风速的情况下的太阳辐射误差，选择其中辐射误差最小的尺寸。阵列式热电偶辐射误差仿真部分中，对涂覆了不同太阳辐射吸收率材料的热端探头及铂电阻冷端补偿使用上述类似的CFD方法进行仿真计算。将辐射误差数据采用支持向量机算法进行数据拟合，得到太阳辐射误差修正公式。实验部分则将阵列式热电偶温度采集电路放入低气压风洞与太阳模拟试验平台进行对比分析和证，探究该设计的可行性和准确性。

2.2 传感器探头的模型建立、网格划分及流固耦合分析

首先通过Pro/E建立了4个直径分别为0.3、0.2、0.1和0.05 mm的热电偶传感器探头模型如图5所示。采用了T型热电偶，其测量范围为-200～350 ℃，符合30 ～ 80 km高空的大气环境。然后利用ICEM对建立的模型进行材料点定义和网格划分，网格参数如下：探头直径分别为0.3、0.2、0.1、0.05 mm。除了直径为0.05 mm的探头导线线径为0.02 mm外，其余探头导线线径均为0.05 mm。传感器探头周围的空气域AIR尺寸设置为5 mm×3 mm×3 mm。经划分后网格数量约为55万，其质量大于0.36，具体的网格划分情况如图6所示。

图5 热电偶传感器探头Pro/E建模Fig.5 Pro/E modeling of thermocouple sensor probe

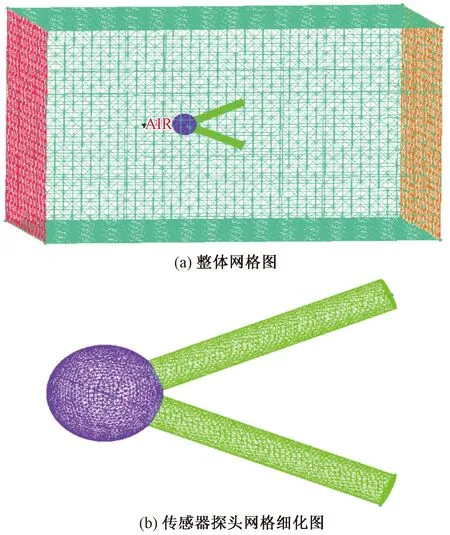
图6 传感器探头网格划分图Fig.6 Grid division diagram of sensor probe

最后使用Fluent软件对传感器模型进行流固耦合分析[7]。根据30～80 km海拔的变化设置空气密度、气体流速设为10～200 m/s，以此环境变量对不同尺寸探头的太阳辐射误差进行仿真分析。当海拔高度分别为80 km和40 km，风速分别为200 m/s和10 m/s时，尺寸分别为0.2 mm和0.1 mm的传感器探头温度场分布如图7所示。其太阳辐射误差分别为0.663 K和0.086 K。

图7 传感器探头温度场分布Fig.7 Temperature field distribution of sensor probe

2.3 传感器探头的仿真结果分析

为了探究不同尺寸传感器探头在不同海拔高度、不同风速的影响下太阳辐射误差的大小，使用计算流体动力学对4个尺寸的热电偶探头进行数值计算，具体的计算结果如图8所示。

由图8可知，对于不同尺寸的传感器探头，气流速度一定时，太阳辐射误差与海拔高度有着相同的增大趋势；海拔高度一定时，太阳辐射误差随着气流速度的增大而减小。当传感器探头直径为0.3 mm，海拔为80 km，气流速度为10 m/s时，太阳辐射误差最大，约为0.911 K。当传感器探头直径为0.05 mm，海拔为30 km，气流速度为200 m/s时，太阳辐射误差最小，约为0.029 K。并且由4幅曲面图对比可知，当海拔与气流速度相同时，传感器探头直径越小，太阳辐射误差越小。由此可见，想要尽可能降低太阳辐射误差对探空温度传感器的影响，应尽可能选用直径较小的探头，因此，阵列式热电偶选用0.05 mm直径的T形热电偶。

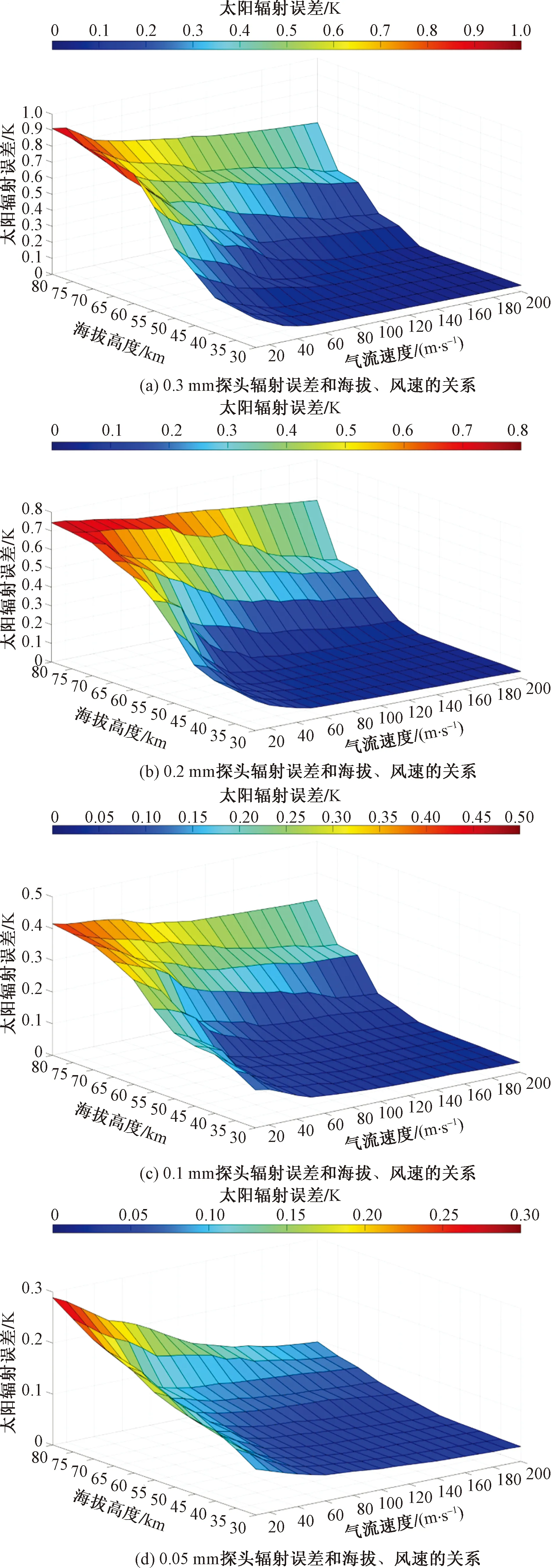
图8 不同尺寸的传感器探头太阳辐射误差和海拔高度、气流速度关系图Fig.8 Relationship between solar radiation error of sensor probes with different sizes and altitude and air velocity

2.4 阵列式热电偶的模型建立、网格划分及流固耦合分析

经上述CFD仿真后，选用直径为0.05 mm的热电偶作为温度传感器，4个热电偶表面涂覆上不同太阳辐射吸收率的材料，间距为2 mm并行排列，确保区域环境的一致性，后端为4个热电偶共用的冷端补偿铂电阻。然后使用ICEM 软件对阵列式热电偶进行网格划分，并将空气域尺寸设为120 mm×120 mm×240 mm。图9为阵列式热电偶温度传感器和周围空气域的网格划分。其中4个并行排列的较小球体为阵列式热电偶的热端探头，位于后方的较大的球体为共用的冷端补偿。

图9 阵列式热电偶传感器及周围空气域网格Fig.9 Array thermocouple sensor and surrounding air grid

采用CFD方法对阵列式热电偶进行仿真分析[8]。将4个热电偶热端探头设置不同的太阳辐射反射率，银质涂层为95%，铝质涂层90%，铜制涂层为50%，黑色涂层为20%，冷端补偿的铂电阻表面太阳辐射反射率也设为95%。如图10所示为仿真时2种情况的阵列式热电偶传感器的温度场分布。将太阳辐射强度设定为1 400 W/m2、海拔高度设为40 km，风速设定为100 m/s时，从左到右分别为银质涂层探头、铝质涂层探头、铜质涂层探头和黑色涂层探头，其对应的太阳辐射误差分别为0.63、0.79、0.96、1.97 K，冷端表面误差升温为0.81 K。当海拔高度设定为80 km、风速设定为10 m/s时，从左到右分别为银质涂层探头、铝质涂层探头、铜质涂层探头和黑色涂层探头，其对应的太阳辐射误差分别为0.91、1.06、1.24、2.88 K，冷端表面误差升温为1.18 K。

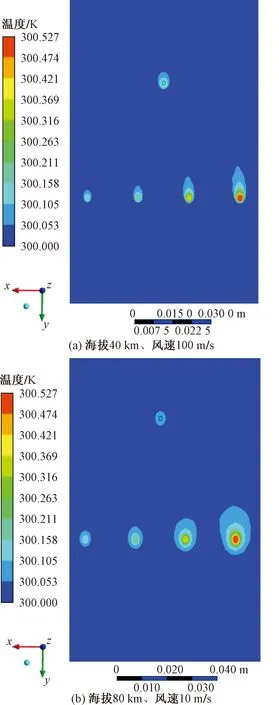
图10 阵列式热电偶传感器温度场分布Fig.10 Temperature field distribution of array thermocouple sensor

2.5 阵列式热电偶的辐射误差比值仿真结果

使用CFD方法对热电偶阵列传感器进行太阳辐射误差比值分析，其中变量为海拔高度和气体流速。海拔高度为30～80 km，气体流速为10～200 m/s，将ΔTd/ΔTa记为黑色涂层热端探头与银质涂层热端探头的辐射误差比值，将ΔTd/ΔTb记为黑色涂层热端探头与铝质涂层热端探头的辐射误差比值，将ΔTd/ΔTc记为黑色涂层热端探头与铜质涂层热端探头的辐射误差比值。经Fluent仿真后的误差比值结果如图11所示。

图11 表面涂覆不同反射率材料的传感器探头误差比值图Fig.11 Error ratio diagram of sensor probe coated with different reflectivity materials

由图11可知，ΔTd/ΔTa在3～3.3上下浮动，在海拔高度为80 km，气流速度为200 m/s时，比值达到最大，为3.27。ΔTd/ΔTb在2.3～2.8上下浮动，在海拔高度为30 km，气流速度为10 m/s时，比值最小，为2.3。ΔTd/ΔTc在1.8～2.4上下浮动，其辐射误差比值最大值为2.39，最小值为1.82。

2.6 辐射误差比值计算及其修正方法

针对各个探头之间的辐射误差比值在一定范围内不稳定，以及CFD仿真对连续模型的分析有所缺陷等问题，使用支持向量机(SVM)算法对各个热电偶辐射误差比值进行修订。对CFD仿真时获取的样本量较少的探空传感器辐射误差预测而言，传统的深度学习方法因为需求的数据量过大并不适合，而SVM算法能以相对较小的数据量，实现较为准确的预测[9]。

支持向量回归预测选用LibSVM作为程序库。首先将海拔高度、气流速度作为SVM的样本输入，不同热电偶探头之间的太阳辐射误差比值作为样本输出。再将样本数据映射到某个特定的数据区间以消除误差较大的数据，达到数据归一化的目的。在训练过中使用归一化处理公式为

(11)

和其对应的反归一化公式为

xi=max(x)-min(x)xi+min(x)

(12)

模型的参数使用直接确定法设置，整个训练集使用通过RBF核函数得出的最佳参数C、g进行训练，获得SVM的预测模型。最后进行数据测试，数据测试用训练得到的模型进行，与CFD仿真实验值进行对比。如图12所示为使用CFD方法仿真的真实值和采用SVM算法拟合的预测值的对比图和误差图。

图12(a)、图12(b)中，预测值与真实值之间误差的均方根为0.045；图12(c)、图12(d)中，预测值与真实值之间误差的均方根为0.037；图12(e)、图12(f)中，预测值与真实值之间误差的均方根为0.051，该结果表明此算法拟合效果良好。将环境因素中的海拔高度与气体流速作为算法的输入，即可得到每个阵列式热电偶传感器探头的辐射误差比值，再由上文推导的式(7)～式(10)计算得到真实的环境温度。

图12 SVM算法拟合值与真实值对比、误差图Fig.12 Comparison between fitting value and real value of SVM algorithm and error diagram

3 硬件设计与实验分析

3.1 硬件设计

图13为火箭下投式探空传感器的硬件电路设计，主要包含主控制器、阵列式温度采集电路、数据通信电路。选用STM32F407ZET6微处理器作为主控制芯片。因为AD7794精度高、通道多、功耗低，并且可将小幅值的信号转换输入ADC，以实现对模拟温度信号的采集和放大[10]，因此选用两个AD7794作为模数转换器，同时处理温度传感器采集的数据以加快运算速度。选用MAX232作为电平转换芯片，使采集到的数据与上位机由串口进行通信。

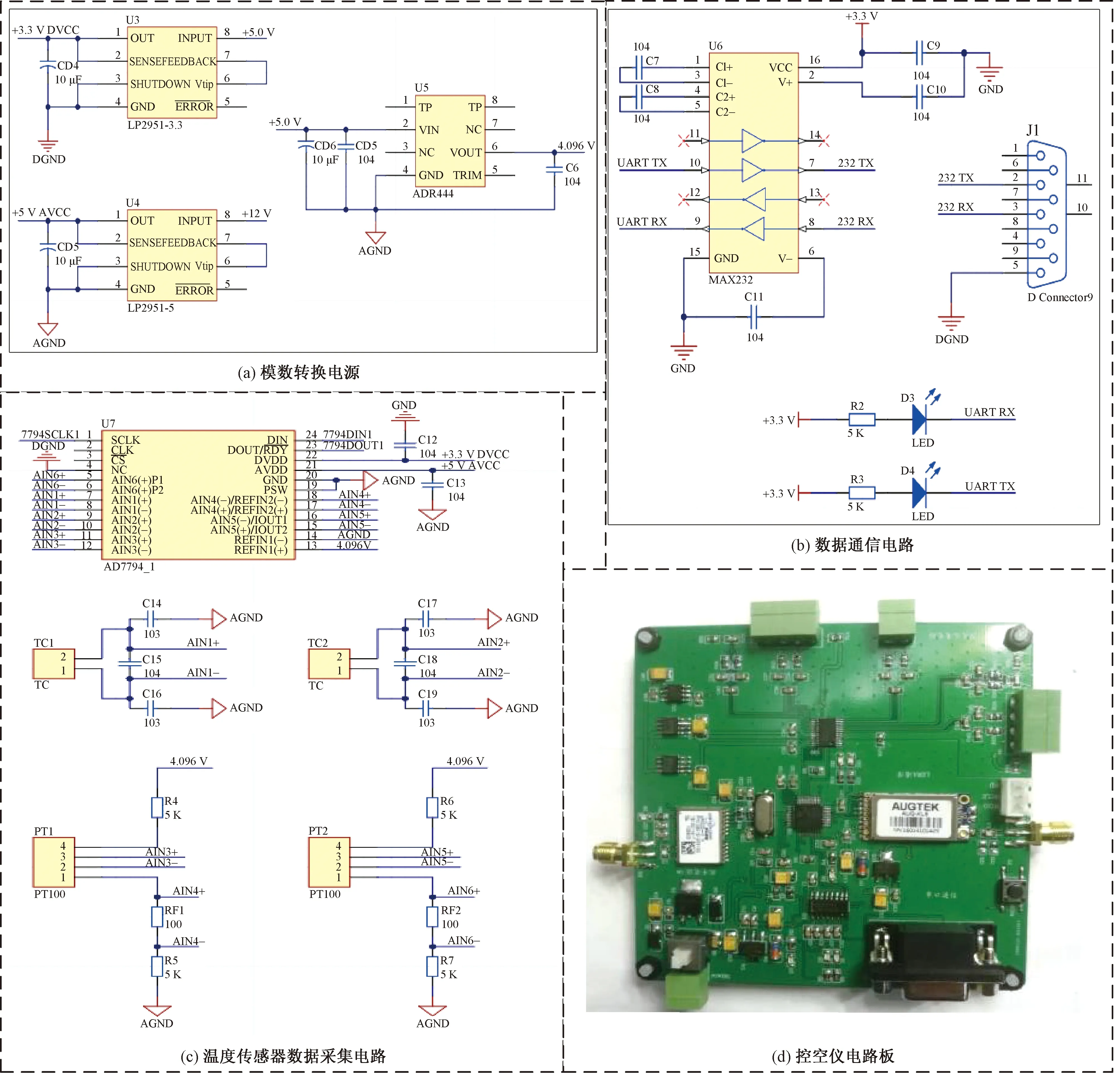
图13 硬件电路设计Fig.13 Hardware circuit design

3.2 实验平台搭建

实验平台选用低气压风洞配合太阳模拟器来模拟真实的超高空大气环境，如图14所示。该平台由以下器件组成如下：2台气泵，其并联工作以模拟出30 km以上高空的大气环境；1个真空腔，作为低气压风洞；1台气压检测仪，保证腔内气压达到设定值；1台气体流速检测仪，用于保证风速达到设定值；1台太阳模拟器，其可产生不同强度的辐射[11]，以模拟真实太阳光照。将阵列式热电偶温度传感器放置在真空腔中心处，使其处于气流与太阳辐射的正中，确保传感器周围环境稳定。

3.3 对比实验及其结果分析

为验证阵列式热电偶温度传感器的测量效果，使用低气压风洞与太阳辐射模拟器作为实验平台对其进行实验，将实验值与仿真值进行比较[12]。太阳辐射强度设为1 000 W/m2，海拔高度设为30～60 km，气体流速设为10～50 m/s。实验结果中部分具有代表性的数据如表1所示。

由表1可知，热电偶阵列中，ΔTd/ΔTa的实验值与经算法拟合后的差值的均值为0.047，ΔTd/ΔTb的实验值与经算法拟合后的差值的均值为0.061；ΔTd/ΔTc的实验值与经算法拟合后的差值的均值为0.057。再通过推导出的式(7)～式(10)计算出环境真实温度，与真实环境温度值进行比较，对照表如表2所示，阵列式热电偶温度传感器的误差均值为0.107 ℃，误差均方根为0.22 ℃。

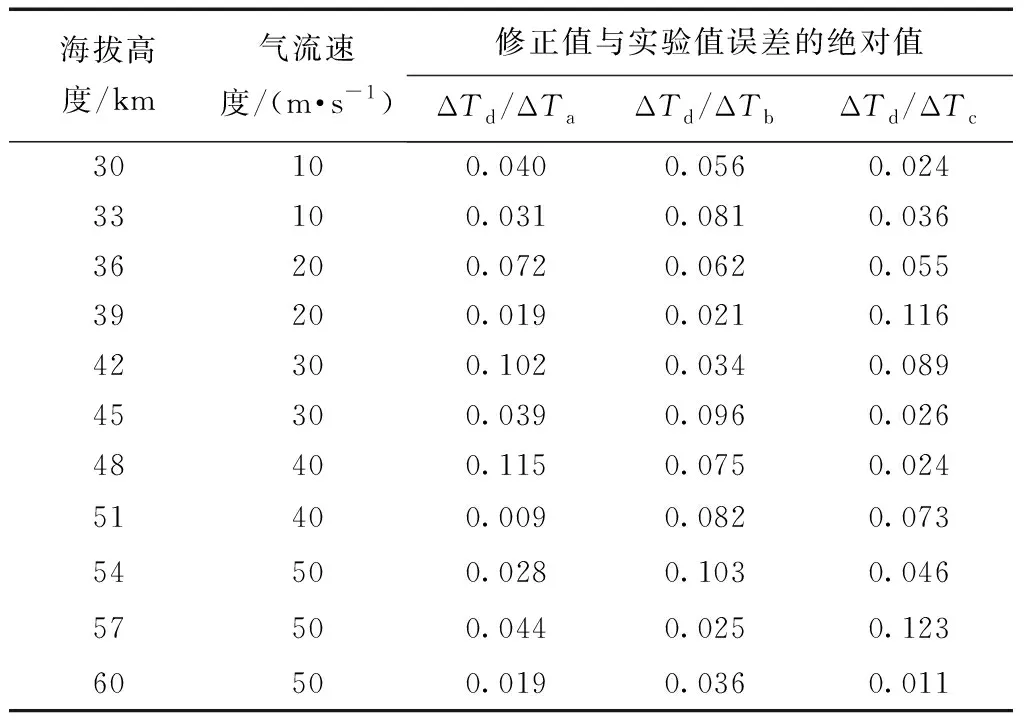
表1 辐射误差比值修正值与实验值对照表Table 1 Comparison between corrected value of radiation error ratio and experimental value

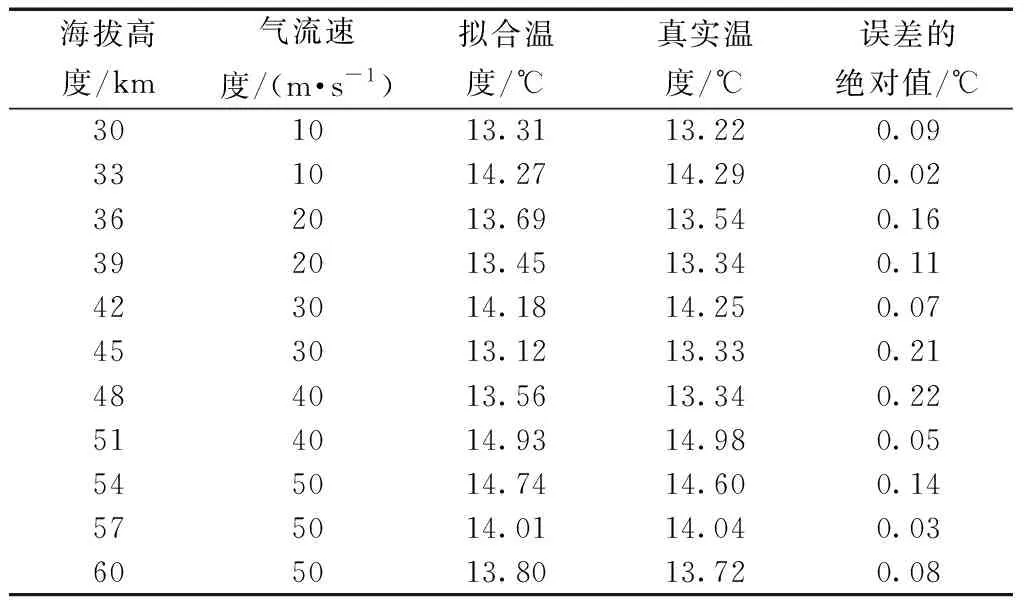
表2 阵列式热电偶测量计算温度与真实温度对照表Table 2 Comparison table of thermocouple array temperature and real temperature

图14 低气压风洞与太阳模拟器实验平台Fig.14 Low pressure wind tunnel and solar simulator experimental platform

4 结论

设计的火箭下投式探空传感器用于探测超高空(30～80 km)大气环境，其搭载了表面反射率不同的热电偶探头从而进行阵列式测温，以降低太阳辐射误差。首先用CFD方法计算出不同尺寸的热电偶温度探头中的探测效果最优者。再针对这一尺寸的探头，用同样的方法计算出每个表面涂覆了不同太阳辐射吸收率材料的热电偶探头的辐射误差，以其之间的辐射误差比值可算出环境温度真实值。再使用支持向量机算法对仿真数据进行数据融合处理。最后以低气压风洞和太阳模拟器作为实验平台进行验证研究，得出以下结论。

(1)对于不同尺寸的热电偶探头，当气流速度一定时，太阳辐射误差与海拔高度有着相同的增大趋势；海拔高度一定时，太阳辐射误差与气流速度呈负相关。当海拔与气流速度都相同时，热电偶传感器探头直径越小，太阳辐射误差越小。

(2)阵列式热电偶温度传感器的各个探头涂覆了不同反射率材料，经计算流体动力学仿真后的各个探头之间的辐射误差比值与经SVM算法数据融合后的误差比值的均方根为0.037～0.051。说明选用的SVM算法数据融合效果良好，经过处理的数据在一定程度上提高了传感器的测量精度。

(3)采用的阵列式热电偶温度传感器的温度测量误差的均值为0.107 ℃，均方根为0.22 ℃，减小太阳辐射误差的效果良好，精度满足超高空大气环境观测的要求。

所提出的火箭下投式探空传感器采用阵列式热电偶作为测温仪器，具有较好的测量精度与较快的测量速度。但未考虑探空仪下落过程中的剧烈摆动引起的太阳高度角和风速的突变等因素的影响。后续的研究中会对传感器物理模型进行优化，并将其放在更加优化的实验平台测试，以模拟出更接近超高空的大气环境，从而进一步验证其可靠性。