矩形巷道顶板围岩塑性区分析与支护设计*

陈 菲，曹宇翔，闫世平，谷拴成，王 盼

(1.陕煤集团神木柠条塔矿业有限公司，陕西 榆林 719300；2.西安科技大学 建筑与土木工程学院，陕西 西安 710054)

0 引言

煤炭作为最重要的基础能源与工业原料，对国民经济发展起着举足轻重的作用。随着地下开采不断向深部发展，巷道顶板的稳定性受到了广泛的关注，顶板的稳定性不仅影响着安全生产，也影响着矿井生产的经济效益。现阶段对顶板稳定性的研究主要着眼于巷道顶板冒落研究，相关研究表明，巷道冒顶实质上是由于巷道顶板围岩的大范围塑性破坏引起的[1]，因此选择合理并符合实际的巷道顶板围岩塑性区的分布计算方法十分重要[2]。为此国内外众多学者[3 -6]对巷道围岩塑性区范围开展了广泛的研究。19世纪50年代，H·卡斯特奈[7]借助理想弹塑性理论，依据Mohr-Coulomb强度准则推导了经典的芬纳 -卡斯特耐公式，马念杰等[8]通过理论计算研究了圆形巷道围岩偏应力场与塑性区之间的关系。王卫军等[9]采用理论计算与数值模拟相结合的方法，对巷道围岩塑性区半径及其分布形态与支护阻力的关系进行了研究。现阶段对巷道顶板围岩力学性质的理论研究大多基于圆形巷道进行[10 -13]，但在实际生产中普遍采用矩形巷道，对于矩形巷道顶板围岩塑性区的确定主要通过数值模拟与现场监测的方法进行[14 -16]。因此有必要对矩形巷道顶板围岩塑性区的确定展开理论研究。

为此，依托弹塑性理论，考虑巷道顶板围岩材料抗拉压强度不等的情况，通过建立矩形巷道顶板梁模型，以顶板梁跨中截面上的最大正应力不超过围岩的极限抗压强度为条件对最大塑性区高度进行理论研究，并以此为依据对顶板围岩进行支护设计研究。为验证理论的适用性，进一步结合实际对柠条塔煤矿S1231掘进工作面胶运顺槽巷道顶板进行监测，将现场实测结果与理论计算的巷道顶板围岩最大塑性区高度进行对比分析，同时提出评价围岩稳定性的方法，对提出的支护设计方案的合理性进行验证。

1 巷道顶板塑性区模型分析

1.1 基本假定

巷道顶板围岩的变形主要以竖向变形为主，且最大竖向变形发生在巷道顶板中部。基于现场观测结果，提出以下假定：①取研究对象为开挖后的巷道断面，按平面应变问题进行分析；②岩体是连续、均质、各向同性、抗拉抗压强度不等的理想弹塑性材料；③作用于矩形巷道顶板荷载主要为上覆岩土体自重荷载，不考虑水平力对顶板围岩竖向变形的影响；④忽略计算范围内岩体自重的影响。

根据以上假定，建立如图1所示力学模型。图1中，q为巷道顶板围岩上覆岩土体自重，kN/m2；b为顶板梁宽度，m；2l为顶板梁长度，m；2h为顶板梁高度，m。

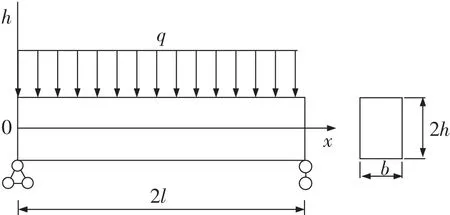
图1 矩形巷道顶板梁模型Fig.1 Roof beam model of rectangular roadway

1.2 顶板弹塑性岩梁截面分析

在上覆岩土体自重作用下，顶板梁截面上应力分布随着煤岩体材料进入塑性阶段的不同有以下4种情况，其截面应力分布如图2所示。图2中，σst为顶板围岩极限拉应力，MPa；σsc为顶板围岩极限压应力，MPa；β为顶板围岩材料抗压强度与抗拉强度之比；e为中性轴偏心距，m；y为顶板梁上层弹塑性区交界处距梁中性轴的距离，m；βy为顶板梁下层弹塑性区交界处距梁中性轴的距离，m。当弹性区高度为2h的顶板围岩形成的梁截面处于极限弹性状态时(图2(a))，梁最下侧受拉纤维正应力达到极限拉应力，此时梁截面对应的弯矩为弹性极限弯矩；当弯矩超过弹性极限弯矩后，梁截面受拉区逐渐进入塑性状态，考虑到梁材料抗压强度与抗拉强度不等，中性轴将不断上移(图2(b))，与此同时，梁截面上部受拉区应力逐渐达到极限压应力(图2(c))；当整个截面受压区应力达到极限压应力时，梁截面全部进入塑性状态(图2(d))，此时梁截面对应的弯矩值为塑性极限弯矩。

图2 顶板梁截面弹塑性阶段演化图Fig.2 Elastoplastic phase evolution diagram of roof beam section

当梁截面处于弹性状态时，截面拉应力达到极限拉应力，此时顶板梁截面弹性极限弯矩为[17]

Me=2bh2σst/3

(1)

式中，Me为弹性极限弯矩，MPa。

根据图2(c)所示的应力分布，由轴力为零可列出式(2)

(2)

化简得偏心距为

(3)

由式(3)可知，当顶板梁处于弹性状态时，有e=0；当顶板梁处于完全塑性状态时，有y=0,e=h(1-β)/1+β，考虑为煤岩体材料，取β=1/6，则e=0.71h，即0≤e≤0.71h。可见偏心距是一个较大的量，在计算时不可忽略。

当梁截面处于弹塑性状态时，如图2(c)所示，截面压应力达到极限压应力时，顶板梁截面弹塑性弯矩为

(4)

式中，Mep为弹塑性弯矩，MPa。式(4)化简得

(5)

当y=0时，即截面全部处于完全塑性状态，如图2(d)所示，代入式(3)，此时截面弯矩为

(6)

式中，Mp为极限塑性弯矩，MPa。

以顶板梁跨中截面上的最大正应力不超过围岩的极限抗压强度为条件，可得顶板梁处于极限塑性状态时梁高与围岩极限抗压强度之间的关系为

(7)

式中，σmax为顶板梁跨中截面最大正应力，MPa；y′为计算点到中性轴的距离，m；I为惯性矩,m4；hp为顶板最大塑性区高度，m。根据式(7)可得，巷道顶板最大塑性区高度为

(8)

(9)

式中，C为粘聚力，MPa；φ为内摩擦角，(°)。同时，根据式(1)、式(6)可得跨中截面处于完全塑性状态时顶板梁所能承受的极限荷载为

(10)

式中，q*为顶板梁所能承受的极限荷载，kN/m2。

2 顶板围岩塑性区高度影响因素分析

2.1 岩层物理力学参数

在得到巷道顶板塑性区高度理论计算公式后，进一步对影响塑性区高度的物理力学参数进行分析。分析时相关参数取自柠条塔煤矿S1231掘进工作面胶运顺槽巷道，巷道平均埋深160 m，巷道断面尺寸6 m×3.75 m(宽×高)，煤层平均厚度为6.87 m，老顶一般厚度为13.40 m，以细粒砂岩为主。直接顶一般厚度为10.30 m，以细粒砂岩为主。底板一般厚度为8.85 m，以碳质泥岩为主。岩层物理力学参数见表1。

表1 岩层物理力学参数

2.2 巷道宽度与埋深的影响

取表1所列围岩物理力学指标，分别选取不同埋深H(100～500 m)，不同巷道宽度(4～7 m)。根据本文理论，对不同埋深、不同巷道宽度的巷道顶板围岩塑性区范围进行计算，计算结果列于表2。

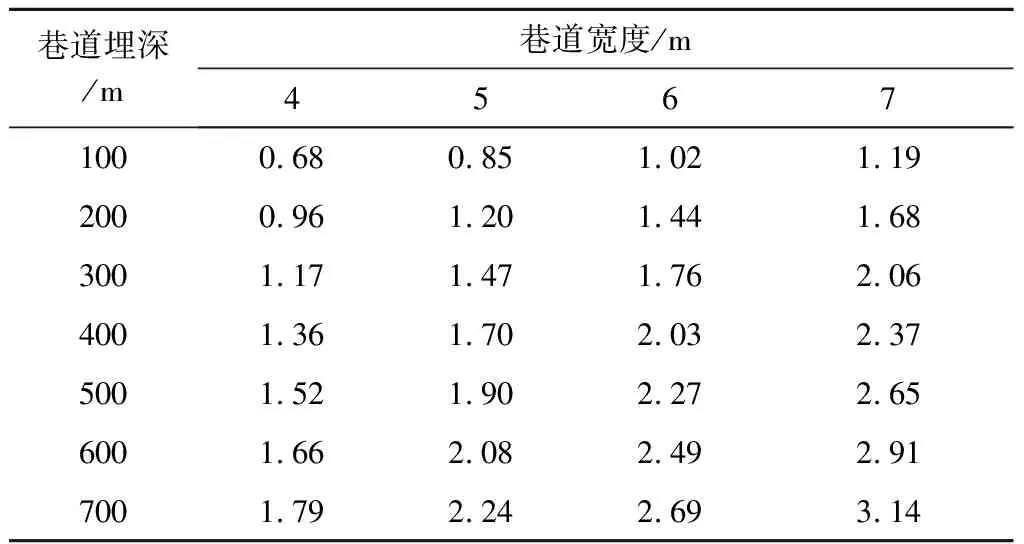
表2 顶板围岩塑性区高度计算结果

计算表明，当巷道宽度一定时，巷道顶板围岩塑性区高度随着巷道埋深的增加而增加；当巷道埋深一定时，顶板围岩塑性区高度随巷道宽度的增加而增加，具体变化趋势如图3所示。

同时可得，当巷道埋深较大时，可适当减小巷道宽度以减小巷道顶板围岩塑性区的高度从而保证巷道顶板围岩的稳定性。

图3 顶板围岩塑性区高度随巷道埋深与宽度变化规律Fig.3 Variation law of plastic zone height of roof surrounding rock with roadway buried depth and width

2.3 顶板围岩粘聚力及内摩擦角的影响

进一步研究顶板围岩粘聚力对顶板塑性区范围的影响，保持巷道顶板围岩其他物理力学指标不变，通过改变巷道顶板的粘聚力和内摩擦角研究巷道顶板塑性区分布规律。结合本文理论公式，可得粘聚力、内摩擦角与最大塑性区高度关系如图4所示。

图4 顶板围岩塑性区高度随粘聚力及内摩擦角的变化规律Fig.4 Variation law of plastic zone height of roof surrounding rock with cohesion and internal friction angle

由图4可知，巷道的周边围岩参数对巷道顶板塑性区高度范围有一定影响，当顶板围岩其他物理力学参数一定时，顶板围岩塑性区高度随粘聚力、内摩擦角的增加而减小，且随粘聚力增加而减小的趋势有所减弱。

3 基于围岩塑性区的锚杆支护设计

锚杆长度可取为顶板梁处于极限塑性状态下所对应的塑性区高度，因此锚杆长度为

(11)

式中，lg为锚杆长度，m；k为安全系数，可取为1.3。

锚杆直径可根据预紧力来确定

(12)

式中，d为锚杆直径，mm；N为锚杆预紧力，kN；σt为钢筋抗拉强度，MPa。

依据经验，锚固段长度约为锚杆直径的30倍，故可据此计算锚杆的锚固长度

l1=30d

(13)

式中，l1为锚杆锚固长度，mm。

将锚杆视为顶板梁结构中的箍筋，可根据《混凝土结构设计规范》中，对于结构受剪时箍筋的确定方法来计算锚杆的间距[18]。

(14)

式中，V为顶板梁所受剪力，kN；Asv为锚杆截面面积，mm2；s为锚杆间距；mm。

(15)

根据理论计算公式，结合柠条塔煤矿S1231掘进工作面胶运顺槽巷道围岩参数进行巷道顶板的锚杆支护设计，支护设计参数见表3。

表3 顶板围岩支护参数

4 巷道监测及稳定性分析

根据表2计算结果，理论计算的柠条塔煤矿S1231掘进工作面胶运顺槽巷道顶板围岩最大塑性区高度为1.35 m，为验证理论计算结果的适用性，进一步对现场巷道顶板情况进行监测。

4.1 测点布置与图像采集

测站布置在柠条塔煤矿S1231掘进工作面胶运顺槽巷道。在巷道顶板中部钻进深7 m的窥视孔，通过窥视仪对顶板内部情况进行观测，以此评估顶板内部破坏情况。窥视结果如图5所示。

4.2 监测结果分析

结合窥视结果，发现在距离顶板深1.0 m处，窥视孔孔壁破碎严重，表明此处高度范围内的围岩发生了塑性破坏，在距顶板深1.5 m、2.0 m、2.5 m处，窥视孔孔壁较为光滑，没有发生塑性破坏，由此可进一步确定顶板围岩塑性区高度在1.0～1.5 m。实测结果表明，巷道开挖后，顶板围岩最大塑性区高度为1.0～1.5 m，与理论计算结果1.35 m基本一致，本文理论的现场适用性得到了验证。

图5 顶板围岩窥视图像Fig.5 Peep image of roof surrounding rock

4.3 围岩稳定性分析

根据巷道顶板梁承担的荷载与极限荷载来定义围岩稳定性系数

(16)

式中，K为围岩稳定性系数；q*为围岩的极限荷载；q为顶板围岩承受的荷载。

当K≥1时，表示顶板围岩所承担的荷载小于等于围岩的极限荷载，K值越大，顶板围岩稳定性越好；当K<1时，则表示顶板围岩承受的荷载大于围岩的极限荷载，顶板围岩稳定性很差。根据柠条塔煤矿S1231掘进工作面胶运顺槽巷道围岩参数进行计算可知稳定系数K=3.2>1，围岩稳定性较好，支护设计较为合理。

5 结论

(1)建立了矩形巷道顶板梁模型，考虑围岩抗拉压强度不等时，对模型进行弹塑性分析，以顶板梁跨中截面上的最大正应力不超过围岩的极限抗压强度为条件，得到巷道顶板最大塑性区高度计算公式。

(2)理论计算所揭示的顶板围岩塑性区变化规律为：①巷道埋深越大，最大塑性区高度也越大；巷道宽度增加，最大塑性区高度也会增大。②围岩粘聚力及内摩擦角的增大能大幅降低顶板围岩塑性区高度。

(3)通过对柠条塔煤矿S1231掘进工作面胶运顺槽巷道的顶板围岩进行监测，对理论计算结果的适用性进行评估。监测结果表明，巷道开挖后顶板围岩的塑性区高度在1.0～1.5 m的范围内，与理论计算结果一致，验证本文理论的现场适用性。

(4)基于顶板围岩塑性区提出了锚杆支护设计方法，并对柠条塔煤矿S1231掘进工作面胶运顺槽巷道顶板围岩进行支护设计，同时运用本文定义的围岩稳定性评价方法对支护设计进行评价。结果表明，围岩稳定性较好，支护设计较为合理。