一类确定性小世界超网络特性分析

李发旭，卫 良

（1.青海师范大学计算机学院，青海西宁 810008；2.青海师范大学数学与统计学院，青海西宁 810008；3.青海师范大学藏语智能信息处理及应用国家重点实验室，青海西宁 810008）

现实世界中，用超图表示的超网络更有利于刻画真实网络的某些性质[1-2]。为了深入理解网络的结构与功能、行为之间的关系，学者们建立了多类超网络模型[3-10]。其中，随机演化模型虽能反映现实网络的某些特性，但无法清晰地描述网络的形成、节点间的相互作用。因此，确定性网络模型引起了学者们的兴趣[11-15]。目前，基于超图结构的确定性超网络的研究成果相对较少[16-19]。该文基于超图理论构建了一类新的确定性超网络模型，分析了几个主要的拓扑特性，并给出了该模型的拉普拉斯谱的递推关系式。

1 确定性超网络建模

为了研究复杂网络的演化过程和结构特性，研究者们提出了各种各样的解决不同实际网络问题的超网络模型，并在此基础上进一步研究了这些网络的特性。该文提出了一种通过节点反复迭代而生成的确定性超网络模型，下面给出此超网络模型的演化和生成机制。

设t为超网络演化的时步数，Nh,t表示t时步生成的确定性超网络，则模型构建过程如下：

1）当t=0 时，设初始超网络Nh,0有h≥2 个节点，以及一条包含h个节点的超边；

2）当t≥1 时，在Nh,t-1中的每个节点新生成一条超边，每条新生成的超边中都新增h-1 个新节点；

3）不断重复2），可得到t时步的确定性超网络Nh,t。确定性超网络模型构建过程如图1 所示，其中h=3。

图1 确定性超网络模型构建过程

从图1 可以观察到，t=2 时步生成的确定性超网络Nh,2是通过将Nh,1中的每个节点用Nh,0超网络结构替换得到的。因此，在t≥1 时步时，只需将超网络Nh,t-1中的每个节点用Nh,0网络的结构替换，即可得到t时步的确定性超网络Nh,t。从网络构造演化过程可以看出，该超网络结构具有自相似特性。

2 确定性超网络拓扑特性

研究超网络拓扑特性的最终目标是了解和掌握拓扑特性是如何影响超网络结构、功能及动力学行为的。只有对超网络的拓扑特性有清晰而明确的认识，才能更深入地探究超网络结构与功能，以及其与超网络动力学行为之间的关系。该文对新构建出的一类确定性超网络的平均超度、超度分布、平均距离和直径等几个主要拓扑参数进行了理论解析，并分析了网络的结构特性，这些工作有助于更好地理解一些真实世界网络的复杂性和多样性。

2.1 平均超度

节点超度是指与该节点关联的超边数目，节点的超度越大说明该节点越居于网络的中心位置，其在网络中的影响力就越大[3]。平均超度是指网络中所有节点的超度的平均值，可以反映超网络的稠密程度。

每个时步，超网络中节点的增加数和超边的增加数分别为ΔN(t)=N(t)-N(t-1)=h[ΔN(t-1)]和ΔE(t)=E(t)-E(t-1)=h[ΔE(t-1)]。

已知N(0)=h,ΔN(1)=h(h-1),E(0)=h和ΔE(1)=h，则ΔN(t)=ht(h-1),ΔE(t)=ht。因此，t时步超网络中包含的总节点数为N(t)=ht+1，超边数为E(t)=

因此，超网络中节点的平均超度为：

由（1）式可知，当t→∞时，=1，说明此类确定性超网络是非常稀疏的。

2.2 超度分布

超网络的超度分布是指在超网络中任意选取一节点，其超度为k的概率。超网络的类型不同，其超度分布也各不相同。

设ti时刻加入超网络中的节点v在t时步的超度为kv(t)，根据超网络的迭代规则可知kv(t+1)=kv(t)+1，所以kv(t+1)=(t-ti)+1。

在t时步，初始时刻的h个节点的超度为kv(t)=t+1。显然，此类超网络的超度分布是离散的，分别为1,2,…,t-1,t,t+1，其对应的节点数分别为ht(h-1),ht-1(h-1),…,h2(h-1),h(h-1),h。因此，超网络的超度分布为：

这意味着超度分布P(k)随着超度k的增加呈指数形式衰减，因此，此类超网络是一个指数网络。

2.3 平均距离和直径

平均距离定义为超网络中所有节点之间最短距离的平均值，用来反映超网络中信息的传输性能和传输效率。网络的平均距离越小，则传输性能越好，传输效率则越高。大多数真实网络都具有较小的平均距离。

设dt表示t时步超网络的平均距离，则有：

其中，Dsum(t)表示t时步超网络中所有节点之间的最短距离之和，如下：

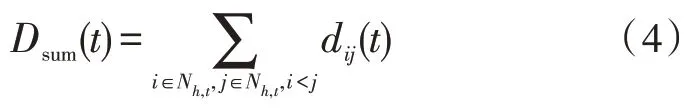
其中，dij(t)表示t时步超网络中节点vi和vj之间的最短距离。

根据超网络模型构建过程可知，超网络具有自相似结构。观察图1 的演化过程可以发现，t+1 时步的超网络Nh,t+1是通过把网络结构Nh,t拷贝h份，然后分别将每个拷贝Nh,t中超度最大的节点依次粘接到Nh,0中的h个初始节点v1,v2,…,vh上得到的，这h个拷贝分别标记为，如图2 所示。

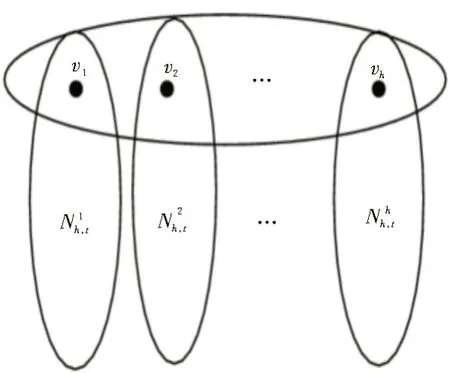
图2 确定性小世界超网络自相似结构示意图

根据该超网络的自相似特性，可以得到如下递推关系：

根据超网络的构造方式和结构的自相似，可得到如下关系式：

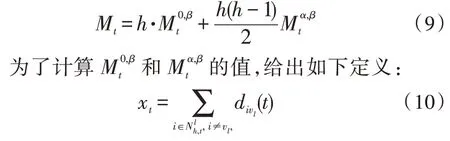
因此，xt满足如下的递归关系：

由于x0=h-1，解式（11）得：

将式（12）代入式（7），计算可得：

将式（12）代入式（8），可得：

将式（13）、式（14）代入式（9），解得：

将式（16）代入式（3）可得t时步超网络的平均距离为：

超网络的直径是指网络中任意两节点间距离的最大值。设Diam(t)表示t时步超网络的直径。由超网络的生成机制可知，初始超网络的直径Diam(0)=1。当t≥1 时，超网络Nh,t的直径由t时步加入到网络中的新节点之间的距离决定。t时步，超网络中任意新节点之间的最大距离至多是Diam(t-1)+2。因此，t时步超网络的直径则满足Diam(t)=Diam(t-1)+2=2(t-1)+1+2。

t时步时，超网络的规模N(t)=ht+1，所以超网络的直径为：

观察式（18）可以发现，此类超网络的直径将随着超网络的规模增大而增大，并呈现对数形式的增长。

3 确定性小世界超网络的拉普拉斯谱

一般来说，超网络的谱性质可以很好地反映其局部结构性质，以及其在超网络上的动力学行为。下面分析确定性小世界超网络的拉普拉斯谱的一些性质。

设Vt={v1,v2,…,vn}为超网络Nh,t的节点集合。t时步超网络Nh,t的邻接矩阵记为A=(aij)n×n，是一个n阶方阵，若节点vi和vj相邻则aij=1，否则aij=0 。令Dt=diag(deg(v1),deg(v2),…,deg(vn))为Nh,t的度对角矩阵，其中deg(vi)=为节点vi的度。超网络Nh,t的拉普拉斯矩阵定义为Lt=Dt-At，则多项式定义为Φ(Nh,t,μ)=det(μIt-Lt)，其中μ为Nh,t的拉普拉斯特征值，It为ht+1阶的单位矩阵。

为了分析该文模型构建的超网络的谱性质，提出一种有效的节点标号方法，将节点按特定的规则进行标号，这种标号规则有助于生成特殊结构的邻接矩阵，以便于计算超网络的特征值。该文提出的节点标号规则如下：

1）超网络Nh,0中初始的h个节点的标号分别为1,2,…,h；

2）在随后的每个时步，超网络中每条新生成超边中新增节点的标号由旧节点的标号i(i=1,2,…,h)及迭代时步决定，新增节点对应的标号分别为i+ht,i+2ht,…,i+(h+1)ht。

上述标号规则可保证超网络中每个节点都具有唯一的标号。对于该文提出的超网络演化模型，在t=2 和t=3 时步时，节点的标号过程如图3 所示，其中h=3。

图3 确定性小世界超网络节点标号过程

由该文提出的超网络的构造规则可知，每个时步由每个旧节点新生成的超边中新增的节点只与当前超边中的旧节点相邻，根据该文给出的节点标号方法，可以方便地获得这种相邻关系。即标号为i+ht,i+2ht,…,i+(h-1)ht的h-1 个新节点只与标号为i(i=1,2,3,…,ht)的旧节点相邻。标号为i的旧节点上新生成的超边中的h-1 个标号分别为i+ht,i+2ht,…,i+(h-1)ht的新增节点之间彼此相邻，而新生成的不同超边中的新节点之间则不相邻。t时步超网络中的ht个旧节点的度均在t-1 时步的基础上增加h-1，而新增的ht(h-1) 个节点的度均为h-1。根据以上分析，可得t时步此类超网络Nh,t的邻接矩阵At和度对角矩阵Dt分别为：

其中，At-1表示t-1 时步超网络的邻接矩阵，It-1为ht阶的单位矩阵，元素对应的是t时步超网络中某一新超边中新增的节点间相邻关系，或是与t-1 时步网络中节点的相邻关系。根据Nh,t构造过程和特定的节点标号规则可知，矩阵At可以看成是一个h×h的块矩阵，且每个块又是一个ht×ht的方阵。

根据拉普拉斯矩阵的定义Lt=Dt-At，此类超网络Nh,t的拉普拉斯矩阵Lt可表示为：

因此，t时步超网络Nh,t的拉普拉斯特征多项式可表示为：

其中，S=It-1(μ-h+1)。

进一步对Φ(Nh,t,μ)化简，可得：

于是，超网络拉普拉斯矩阵特征多项式可写成如下递推关系：

观察式（25）可以发现，t时步超网络有ht+1个特征值，其中有一个重数为ht(h-2)的特征根h，而其余的2ht个特征值则可通过t-1 时步超网络的特征值计算得到。注意到Φ(Nh,t-1,μ) 是一个ht次多项式，多项式最高次项的系数为1，所以1 是多项式的常数项，由此可知，拉普拉斯的特征值中不包含1。

从式（28）不等式可以发现，所有特征值均大于或等于0，且特征值h的重数随迭代时步数的增加呈指数形式增加。

4 结束语

该文结合复杂超网络在模型构建领域的研究，提出了一种新的生成确定性超网络模型的机制。这种新机制即通过节点迭代的方式，在每个时步，超网络中的每个节点新生成一条超边，每条新生成的超边中都新增h-1 个新节点，从而生成一个新型的确定性超网络模型。该文解析了此类确定性超网络的平均超度、超度分布、平均距离和直径等主要拓扑参数。分析结果表明，该确定性超网络是一个稀疏的网络，超度分布服从指数分布，超网络的平均距离和直径都随着超网络规模的增大呈对数形式增长，同时也反映出该超网络具有小世界特性。此外，该文还采用一种有效的节点标号方法，理论推导出拉普拉斯特征值的递推关系式。利用此递推关系可以发现确定性小世界超网络的拉普拉斯特征值分布有如下规律：t时步的超网络拉普拉斯特征值中不含值为1 的特征值，存在一个重数为ht(h-2)的特征值h，其他特征值可利用递推关系式计算得到。显然，文中提出的节点标号方法有效地降低了计算超网络拉普拉斯特征值的时间复杂度。研究结果也揭示出此类超网络的复杂性特征，这种具有自相似特性的网络也表现出了小世界特性，这些研究结果有助于更好地了解实际网络的复杂性和多样性。在后续的研究中，研究者可将研究重点放在改进超网络的生成机制，新构建确定性无标度超网络模型并分析其拓扑性质、网络动力学行为等方面。