考虑需求侧快速响应资源的数据驱动频率约束经济调度
姚 宇,叶承晋,朱 超,丁 一,徐奕乐,王 蕾
考虑需求侧快速响应资源的数据驱动频率约束经济调度
姚 宇1,叶承晋1,朱 超2,丁 一1,徐奕乐3,王 蕾2
(1.浙江大学电气工程学院,浙江 杭州 310027;2.国网浙江省电力有限公司经济技术研究院,浙江 杭州 310008;3.浙江大学能源工程学院,浙江 杭州 310027)
随着可再生能源渗透率的逐步提高,电力系统惯性水平下降,系统频率安全稳定面临挑战,迫切需要配置需求侧快速响应资源参与系统频率调节服务。针对此问题,分析了变频空调、储能和电动汽车提供电力系统调频备用的可行性,建立考虑上述需求侧快速响应资源的频率安全约束联合经济调度模型,以进行源荷双侧调频备用的统一优化。然后,引入基于高维模型表达的数据驱动方法将调频备用与最大频率偏移量之间的高阶非线性、隐式关系转换为低阶、显式表达式,从而实现频率安全约束经济调度模型的简化和求解。最后,结合IEEE 30节点系统验证了所提调度模型和方法的有效性,以及所提的数据驱动频率安全约束可确保系统在不平衡功率下的异常频率在约束范围内,且需求侧快速响应资源对于提升系统频率韧性具有重要正向作用。
需求侧快速响应资源;频率动态模型;频率安全约束联合经济调度;调频备用;高维模型表达
0 引言
随着以新能源为主体的新型电力系统建设推进,电力系统新能源渗透率逐步提高,系统转动惯量出现明显下降[1-2],系统频率安全稳定面临风险。2021年2月,美国德克萨斯州遭遇暴风雪的袭击发生大停电事故,事故发生前光伏和风电发电的比例约为34.5%[3],系统频率备用严重不足,频率最低下降到59.3 Hz,累计切除负荷约20 000 MW,400多万人口受到影响[4]。2019年8月,英国发生大停电事故,事故发生前英国新能源出力占比约30%,事故发生过程中风电系统耐受异常频率的能力不足,脱网严重,频率最低下降到48.8 Hz[5],导致系统低频减载而停电[6]。
长久以来,电力系统依靠调频备用来保障系统功率失衡时的频率安全稳定。因此,为保证充足的调频备用,制定电力系统机组组合和经济调度方案时应考虑频率安全约束[7-10]。然而,频率安全约束高度非线性化,含该约束的优化问题直接求解难度大。目前已有较多研究关注频率安全约束的转化方法:文献[7]将频率安全约束加入机组组合问题中,通过分段线性化的方法,将系统频率最低点的非线性化约束转化为线性化约束;文献[8]构建了包含多种可再生能源的频率最低点指标,将其加入机组组合模型中,使用分段线性化方法使该问题可解。分段线性化是一种简单直观的方法,但它在精度方面存在缺陷,导致经济调度方案在一定的系统功率波动时,可能会出现频率越限的情况。一些学者提出解析法,即通过数学推导将频率安全约束重新表达。文献[9]从频率动态模型中推导出频率最低点解析式,将频率最低点约束引入到考虑风电不确定性的随机机组组合模型中,分别提取决策变量的边界,使得频率最低点约束线性化。文献[10]将频率动态模型用解析方式表达,然而在解析式中引入了指数项、0-1变量相乘、min函数和max函数,过程较为繁琐。以上文献均将频率安全约束用解析的方法写成线性化的表达式,数学推导过程复杂,且会随机组数量的增加而愈发复杂。
随着新能源渗透率的逐步提高,发电侧调频资源稀缺问题进一步凸显,通过需求响应技术发掘负荷侧灵活资源的调频潜力成为研究热点[11-12]。一些快速需求响应资源爬坡速度快于火电机组,可为电力系统提供快速调频备用。文献[13]提出了变频空调参与调频的电热模型,文献[14]分析了聚合空调的调频备用潜力,文献[15]分析了电池储能在调频方面的优势,文献[16]分析了电动汽车参与调频的优势,并提出了考虑用户需求和车辆限制的电动汽车参与调频控制策略。考虑负荷侧资源后,有必要拓展电力系统机组组合和经济调度的建模框架,以实现源荷双侧调频备用的统筹优化配置。但由于负荷的频率动态特性与传统火电机组不同,导致系统频率响应特性发生改变,使得高阶非线性的频率安全约束变得更为复杂。另一方面,随着电力系统不确定性的增强,要求频率约束优化模型的刷新和求解速度进一步提高,因此本文考虑使用数据驱动方法,对考虑需求侧资源的频率安全约束进行低阶转化,以实现经济调度问题的快速解算。
数据驱动方法作为一种黑箱算法,能够直接对模型的输入输出接口建模[17],在复杂物理模型的转换方面具有优势,在频率安全约束的转换中已有一些基础应用。文献[18]从数据驱动视角,线性化频率安全约束,将频率安全转化为一个基于支持向量机的二分类问题,然而该模型只能判断频率是否越限,无法衡量越限的程度。此外,经济调度是一个实时滚动优化的过程,频率安全约束的强度随系统运行状态发生变化,甚至会随着调度员的风险偏好而改变,数据驱动的频率安全约束需要具备应对该种变化的能力。
针对以上问题,本文提出了考虑需求侧快速响应资源的数据驱动频率安全约束经济调度方法。首先,将变频空调、储能电池和电动汽车纳入系统调频框架。然后,构建考虑频率安全约束的源荷双侧联合经济调度模型,以实现调频备用的优化配置。最后,将高阶、非线性的频率安全约束通过高维模型表达转化为低阶约束,实现模型在线求解。
1 考虑需求侧快速响应资源的系统频率调节过程
电力系统运行过程中,不可避免会发生功率扰动而导致系统频率下跌,主要功率扰动源包括负荷激增、发电出力骤降和通道故障。功率扰动量与频率偏移量之间的关系,一般通过电力系统频率动态模型来表达。系统频率下降后,调频资源投入而将异常频率逐渐抬升,直至恢复工频。本文将需求侧资源纳入电力系统调频框架,图1为考虑需求侧快速响应的频率动态模型。
如图1所示,支撑系统频率安全的调节功率由火电机组和需求侧资源共同提供,系统的频率动态模型可表示为
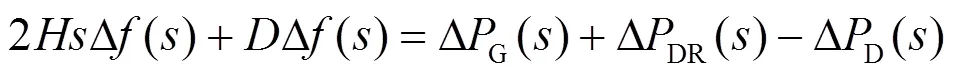
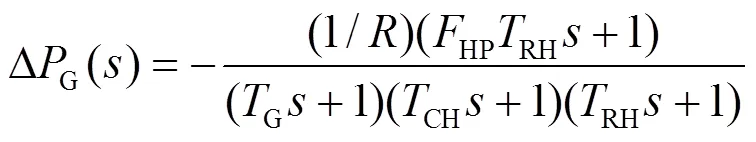
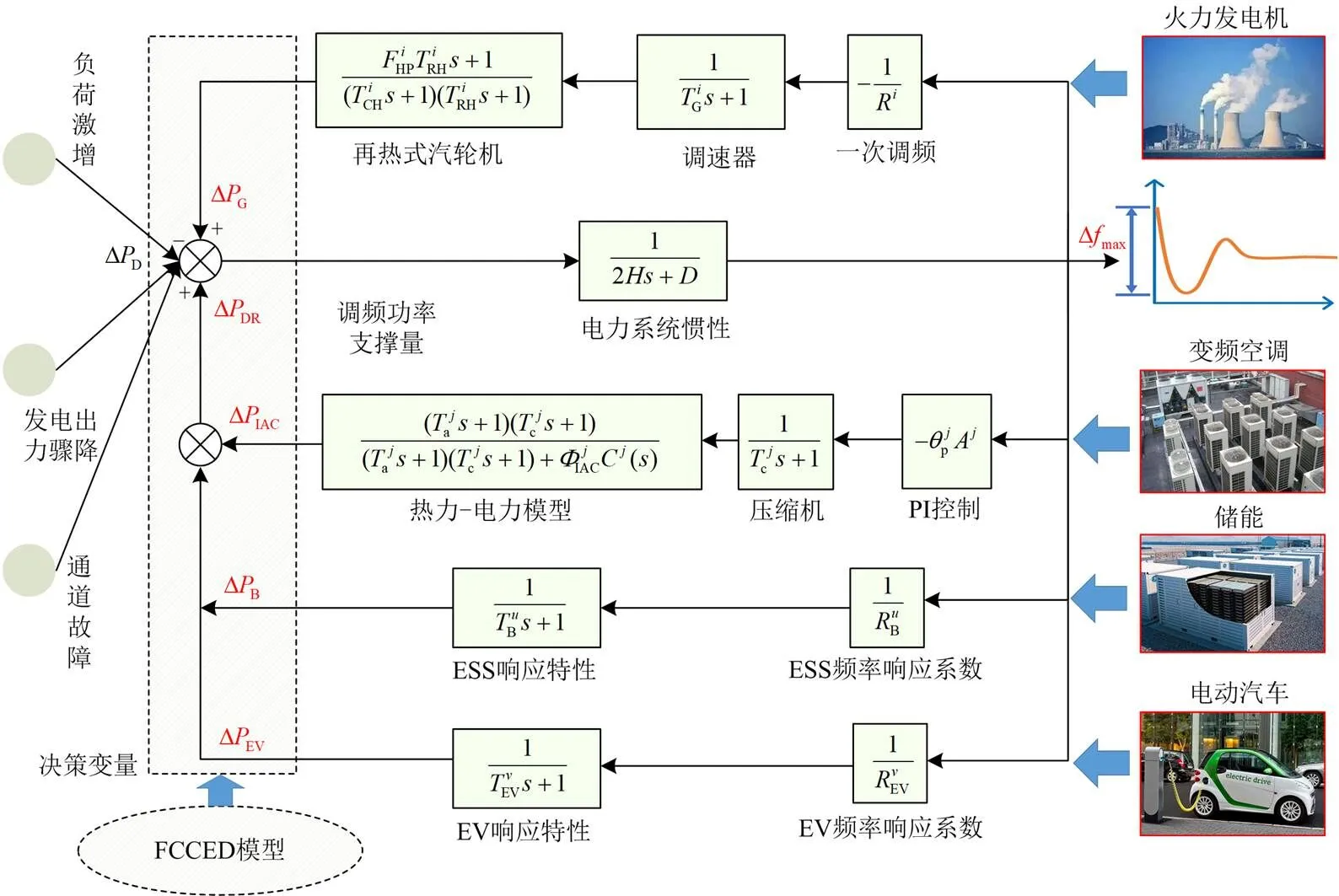
图1 考虑需求侧快速响应资源的频率动态模型
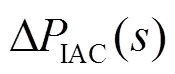
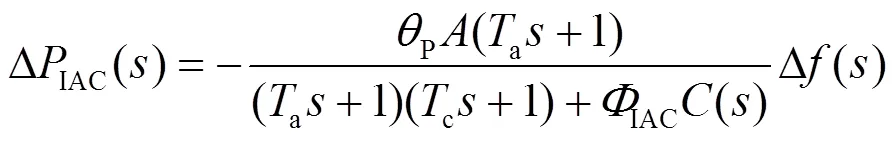
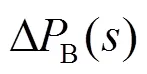
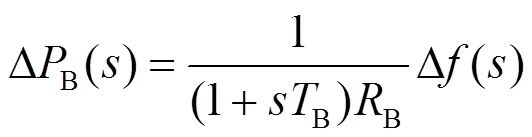
电动汽车在短时间内可调节动态其充电功率,甚至通过V2G反向送电[23],待机状态下达到峰值功率的时间为毫秒级[16],是一种快速调频资源。本文采用的电动汽车模型,通过一阶惯性环节反映双向变流器和动力电池的响应,其频率动态特性可表示为
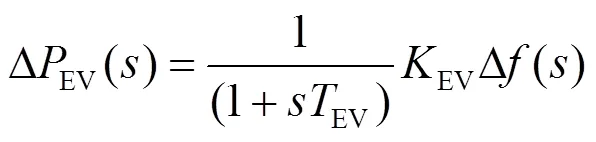
2 频率约束的源荷双侧联合经济调度模型
本节建立FCCED模型,将变频空调、储能电池和电动汽车3种需求侧资源与常规电源纳入经济调度框架中,统一配置其调频备用容量。配置的基本原则是在保障频率安全的前提下,尽可能地使总备用方案成本最低,实现电力系统安全经济运行。
2.1 需求侧快速响应资源的调度模式
配电网中空调、电动汽车、储能等资源单体容量小、电压等级低、分布散,不适合直接参与大电网调频。因此考虑通过负荷聚合商(load aggregator, LA)和储能电站实现分散资源集总参与电力系统调度。本文的经济调度框架如图2所示,负荷聚合商分别聚合配网侧零散的空调、电动汽车和储能电站聚合单体储能,为系统运营商提供可调容量、报价和聚合体的频率动态模型参数。系统运营商(调度中心)对负荷聚合商和储能电站进行经济调度,聚合商直接控制零散空调和电动汽车,储能电站直接控制单体储能。其中,聚合体的频率动态模型参数采用非参数核密度估计方法[24]计算。

图2 基于负荷聚合商的经济调度框架
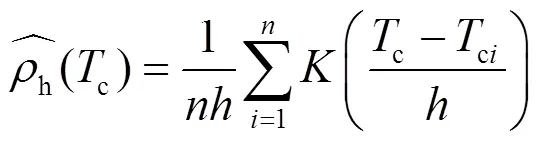
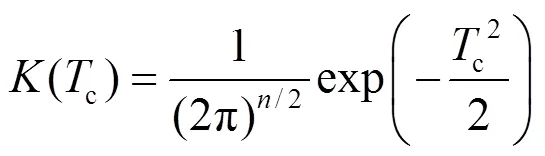
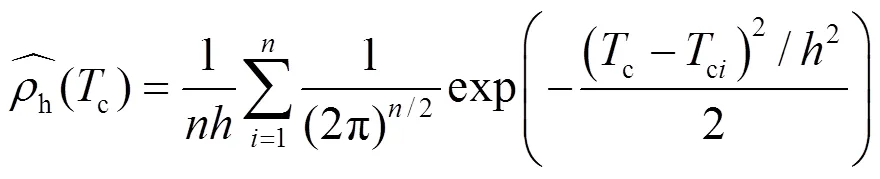
2.2 目标函数
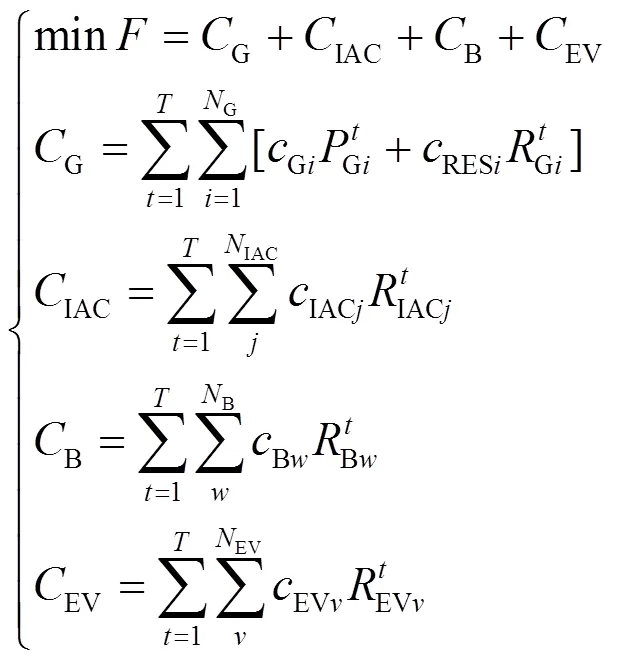
优化目标是全时段的运行成本最低,发电侧成本包含发电机组运行成本和调频备用成本,需求侧成本包含变频空调、储能电池、电动汽车提供调频备用的成本。因此,该机组组合模型的目标函数为
趋势二:京津同城化将成为更加有效地推进京津冀协同发展,进而建立环渤海协同发展新机制的重大战略支点。以北京、天津为中心更加强调京津联动,加快实现京津同城化发展。同城化是区域经济一体化和城市群建设过程中的一个重要阶段,是区域城市间经济和社会发展到一定程度的必然趋势。推动京津同城化,关键是要实现京津基础设施一体化、产业发展一体化、市场一体化、公共服务一体化、资源配置一体化等,共同发挥高端引领和辐射带动作用,成为推动京津冀协同发展,建立环渤海协同发展新机制的重大战略支点。
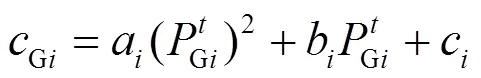
2.3 约束条件
1) 功率平衡约束
系统在所有时段都应当满足发电与负荷功率平衡约束。
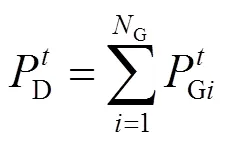
2) 传输容量约束
潮流传输过程中,支路潮流不能超过该支路的传输容量上限。
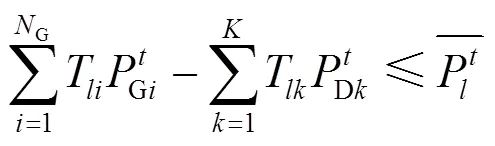
3) 旋转备用约束
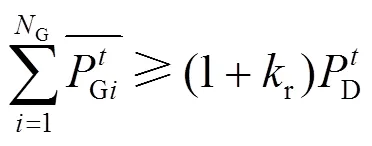
4) 出力约束
机组出力和机组备用还应满足容量约束。
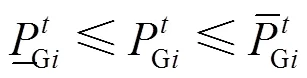
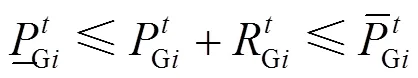
需求侧快速响应资源应同样满足其容量约束。
5) 爬坡约束
机组出力和需求响应资源都应满足爬坡约束,相比于火电机组,需求响应资源爬坡受限较少,爬坡速度较快。
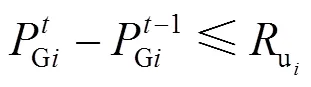
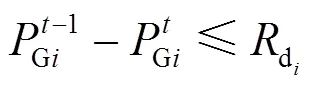
6) 频率安全约束
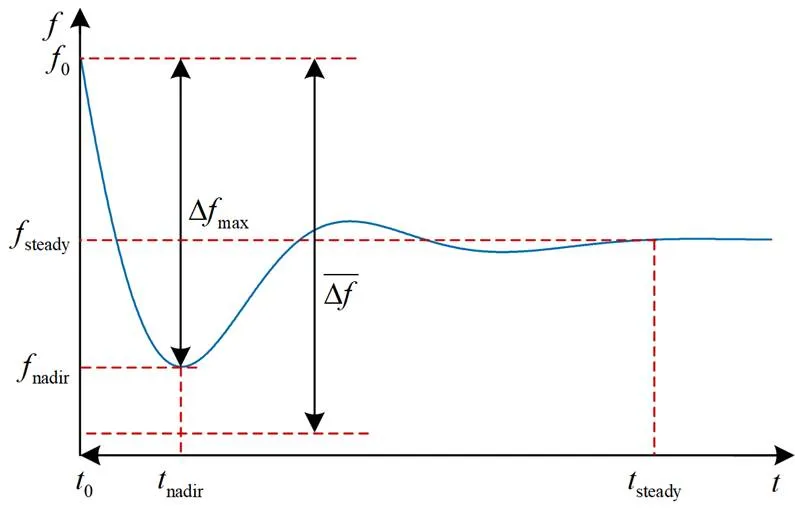
图4 扰动后电力系统频率动态过程

3 数据驱动的频率安全约束转化
为应对式(18)高阶非线性的功率-频率隐关联约束,本节引入数据驱动的HDMR方法将其降阶显式转化,从而使FCCED转为常规优化问题。
3.1 高维模型表达方法
高维模型表达(high dimension model representation, HDMR)方法可将多输入-单输出的非线性系统表达成一种简单的映射关系[29]。式(18)包含了高阶非线性化的复杂频率动态模型,无法直接求解。本文选择HDMR的数据驱动方法对频率安全约束进行刻画,有两方面原因。一方面,频率安全约束所包含的频率动态模型是一个典型的非线性多输入—单输出系统,适合使用HDMR模型简化;另一方面,HDMR方法精度较高、计算速度快[30],可满足电力系统经济调度的精度需求和计算速度需求。HDMR方法原理如下所述。

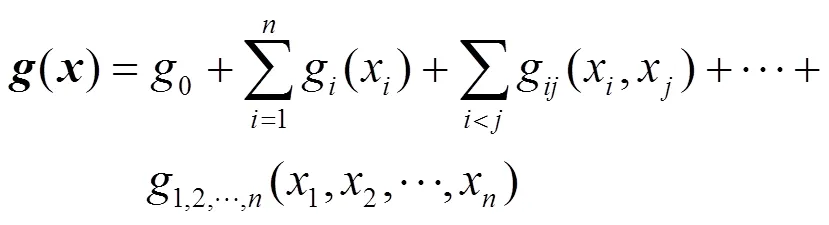
高阶分量对输出的影响很小,可忽略不计。因此,保留到二阶分量,如式(21)所示。
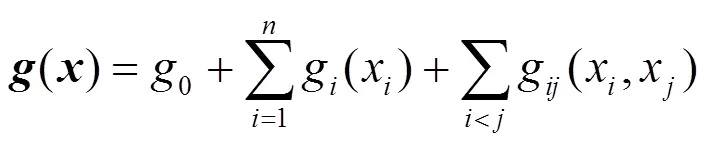
用正交多项式对式(21)进行逼近。
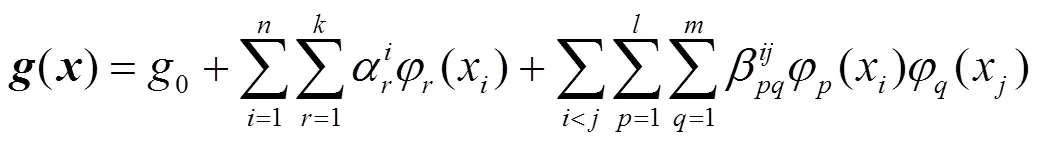
3.2 基于HDMR生成数据驱动的频率安全约束
基于HDMR方法生成数据驱动的频率安全约束的过程如图5所示,包括数据层、驱动层和优化层。

图5 基于HDMR生成数据驱动频率安全约束的流程
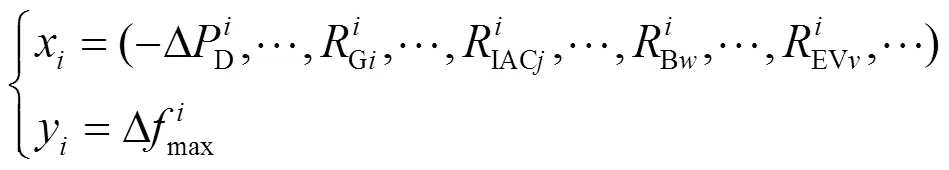
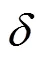
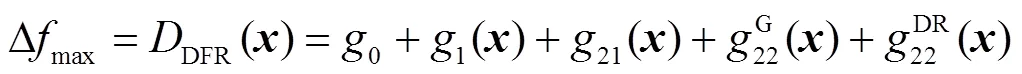

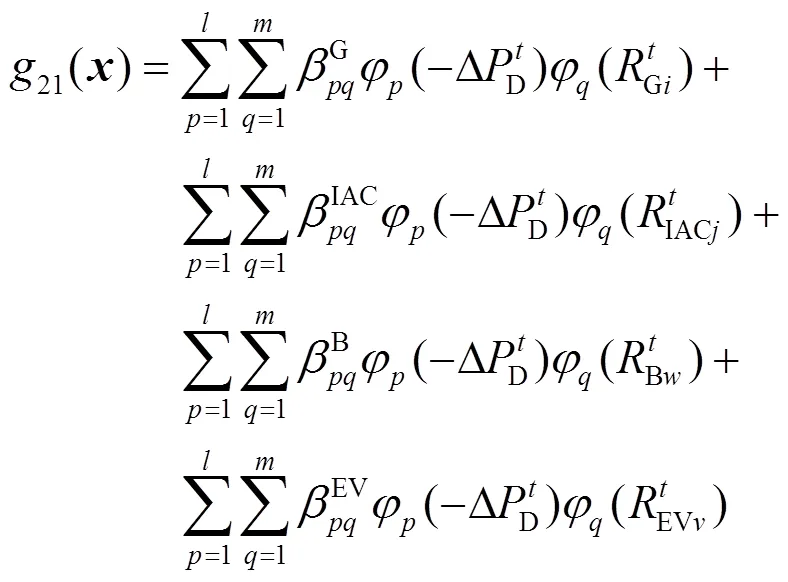
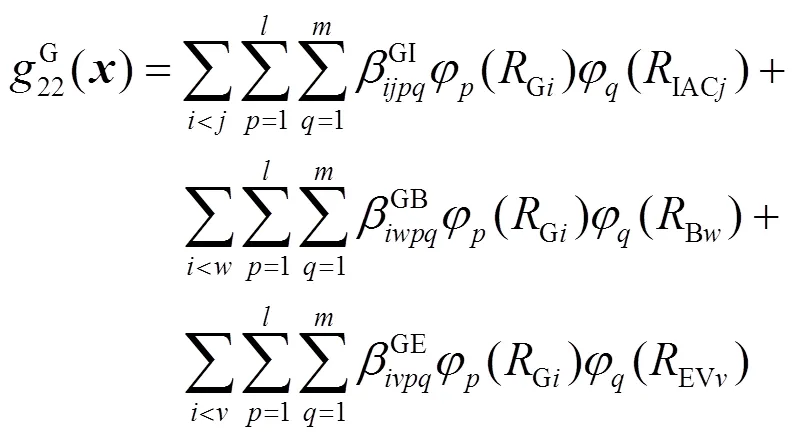
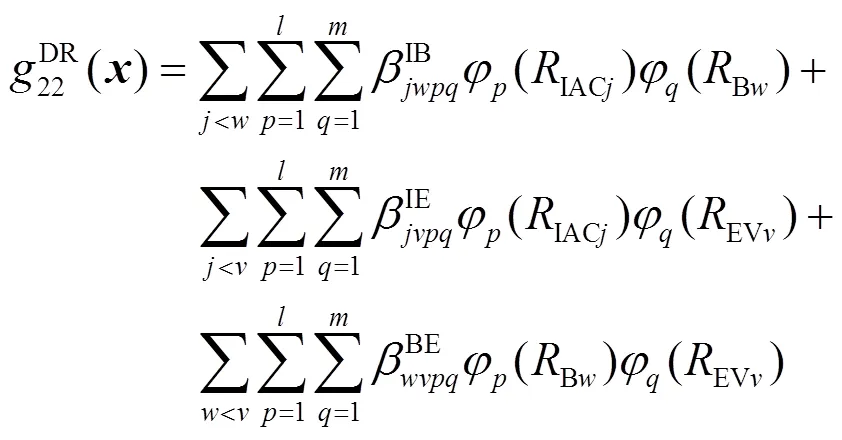
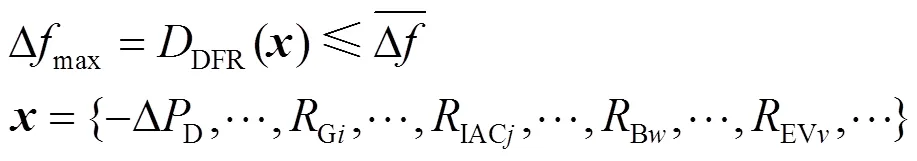
接着,使用式(29)替换式(18),从而将原隐式的高阶非线性频率安全约束经济调度问题转化为BLP(bilinear programming)问题,使用McCormick Envelopes[32]求解。
本文提出的基于HDMR方法生成数据驱动的频率安全约束,满足以下条件:
1) 输入向量的维数不变,即发电机组启停状态、需求侧快速响应资源的响应状态(是否参与调频)都不变。当输入向量的维数发生改变时,重新训练HDMR模型以得到新的表达式。
2) 系统频率不崩溃。若系统发生频率崩溃事故,系统频率会一直下跌,那么不存在频率最低点,此时频率动态模型以及HDMR方法不适用于调频备用与最大频率偏移量之间关系的建模。
本文所研究对象为经济调度问题,即只对发电机组和需求侧快速响应资源的调频备用作优化分配,不改变其启停状态,输入向量的维数不变;本文提出的频率安全约束使经济调度分配足够的调频备用,系统频率在可承受范围内波动,确保不发生频率崩溃,因此满足以上条件,可适合采用HDMR进行模型转化。
4 算例分析
4.1 系统参数
为验证本文所提模型的有效性,采用文献[33]中改进的IEEE30节点系统进行测试,其中7节点负荷改造为储能电站,12节点负荷改造为变频空调集群,21节点负荷改造为电动汽车集群。系统总容量为335 MW,该系统包含6台火电机组。机组参数见表1,负荷数据见表2。

表1 发电机组的参数

表2 各时段总负荷数据
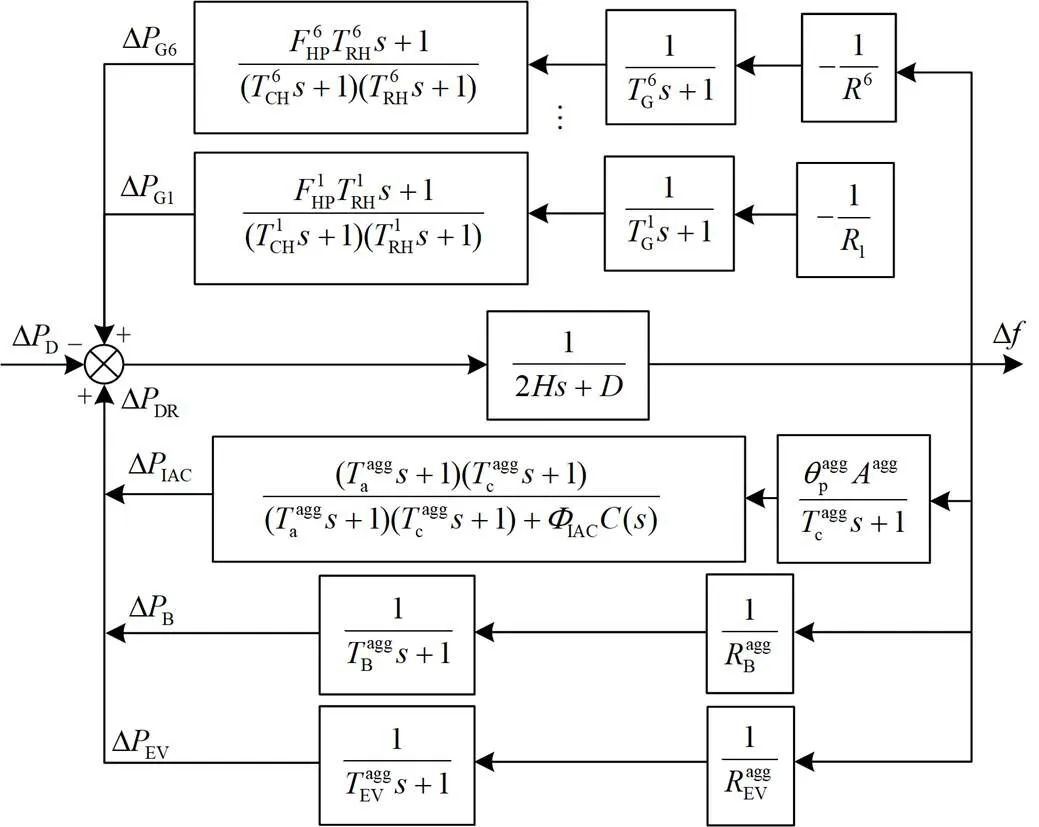
图6 修改IEEE 30节点对应的频率动态模型示意图
IEEE 30节点系统对应的频率动态模型如图6所示。空调、电动汽车由负荷聚合商进行聚合,储能由储能电站聚合。聚合参数通过2.1节中的非参数核密度估计方法得到。以变频空调为例,基于文献[18]中变频空调负荷群数据,核密度估计得到空调聚合体的参数。同理,其他聚合调频参数见表3。变频空调、储能电站、电动汽车的调频备用成本分别取4.2美元/MW、4.0美元/MW、4.1美元/MW[34]。
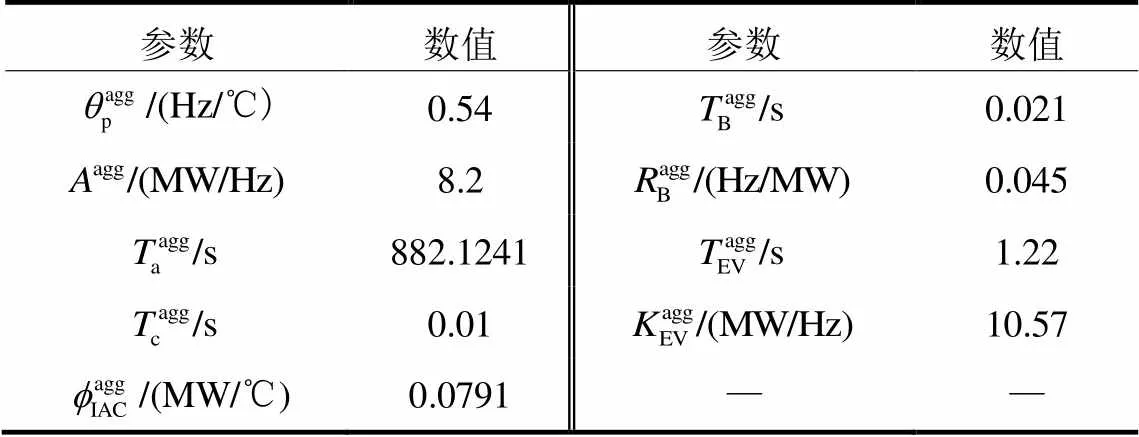
表3 需求侧资源的参数
4.2 基于HDMR生成频率安全约束的精度分析
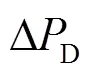
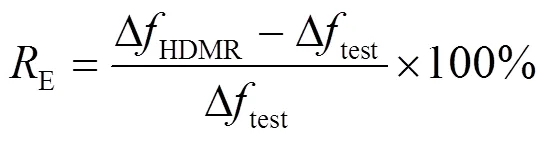
所有测试点的误差散点结果见图7。可见,HDMR方法与图1所示的传统的频率仿真方法相比,最大相对误差不超过17.52%,平均相对误差(mean relative error, MRE)是3.71%,整体精度表现优异,完全满足实际调度应用的需要。
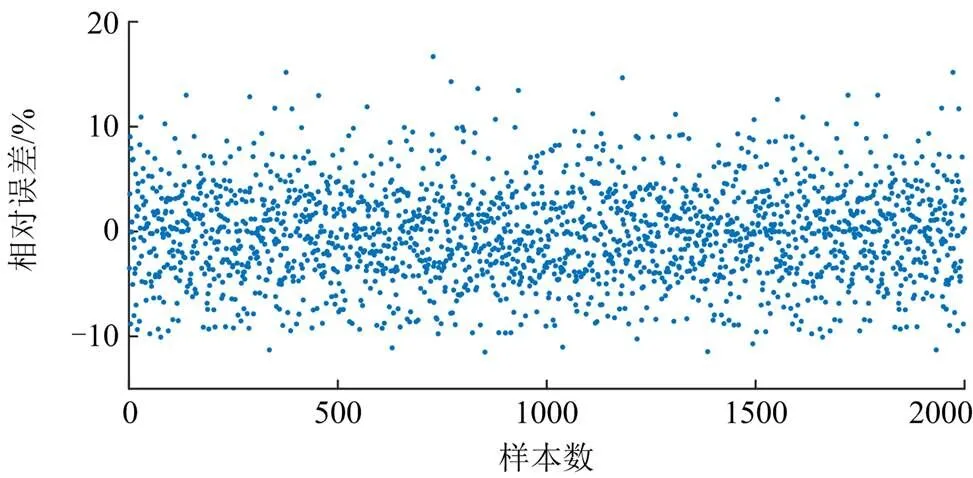
图7 HDMR在测试集的相对误差
为验证HDMR在不同数据集上的精度,本文针对多组样本数据进行了实验。
1) 基于泊松分布产生10 000个功率缺额数据,频率数据、备用数据采用图1所示的频率动态模型计算;
2) 基于均匀分布生成10 000个功率缺额数据,其他步骤同1);
3) 基于指数分布生成10 000个功率缺额数据,其他步骤同1);
4) 基于正态分布生成10000个功率缺额数据,其他步骤同1);
5) 分别基于泊松分布、均匀分布、指数分布、正态分布生成2500个功率缺额数据,组成10 000个功率缺额样本,其他步骤同1)。
5组样本都按照8:2的比例划分训练集和测试集,训练集由10折交叉验证划分出验证集。重复10次实验,获得平均相对误差和最大相对误差。实验结果如图8所示,在5个数据集的10次实验结果中,平均相对误差均不超过4%,最大相对误差不超过17.8%。说明HDMR方法在不同样本数据集上均能体现出较好的拟合效果。
4.3 含频率约束的联合经济调度结果
本节对比了两种场景的经济调度结果。
场景1:在不考虑频率约束的情况下,系统按照各时段总负荷的10%预留调频备用容量,按成本最低准则,分配源荷双侧的调频备用容量。
场景2:在考虑频率安全约束情况下,系统按成本最低原则,分配源荷双侧的调频备用容量。

图8 HDMR方法在不同样本上的相对误差
场景1的调度结果如图9(a)所示,总备用容量约为60 MW,全部由火电机组承担,成本72 914.53美元。场景2调度结果如图9(b)所示,总备用容量约为120 MW,需求侧资源也参与了调频,总成本77 931.54美元。增加频率安全约束后,系统预留备用量提高了1倍,经济调度方案成本增加。
在以上两种经济调度方案下,仿真系统分别在每个时段经历30 MW功率扰动后的频率变化。结果如图10所示,场景1频率最低点均在49.5 Hz以下,在01:00—03:00和20:00—24:00时段,频率甚至降至48.3 Hz以下,远低于系统允许的最低频率49.5 Hz。场景1中,12:00频率下跌最少,然而频率最低点是49.21 Hz,也低于49.5 Hz。场景1的调度方案承受功率扰动的能力差,无法保障频率安全。场景2中,系统在经受相同的功率扰动后,频率最低点均维持在49.6 Hz以上,满足频率安全要求。因此,采用HDMR转化后的FCCED模型能够应对系统功率扰动,保障系统安全稳定运行。
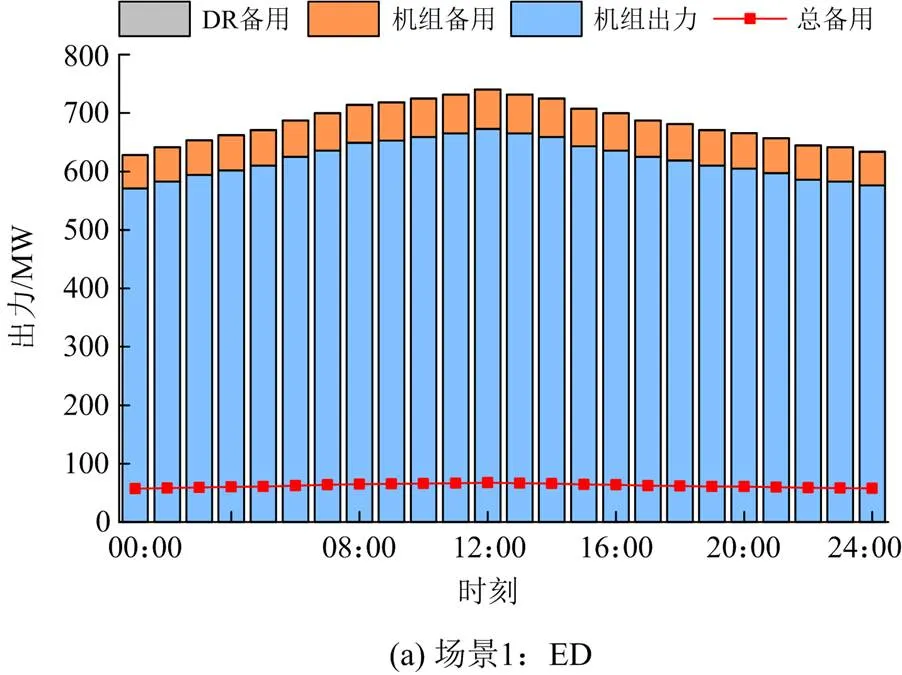
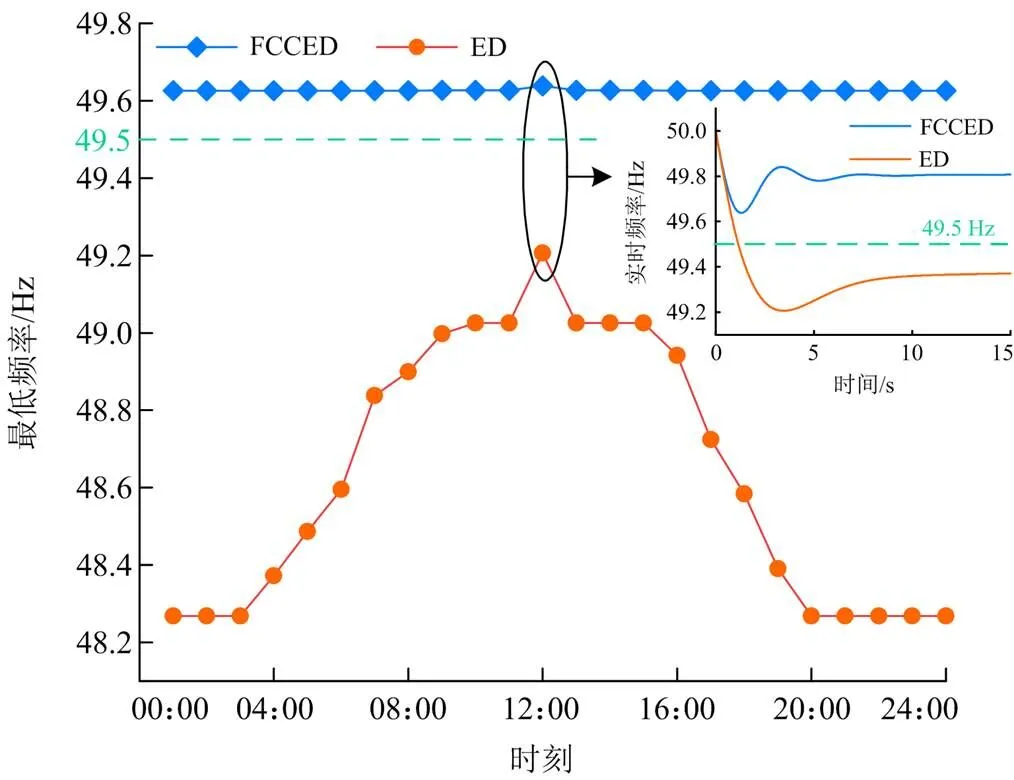
图10 FCCED与ED的频率最低点对比
4.4 需求侧快速响应资源对系统频率安全的作用

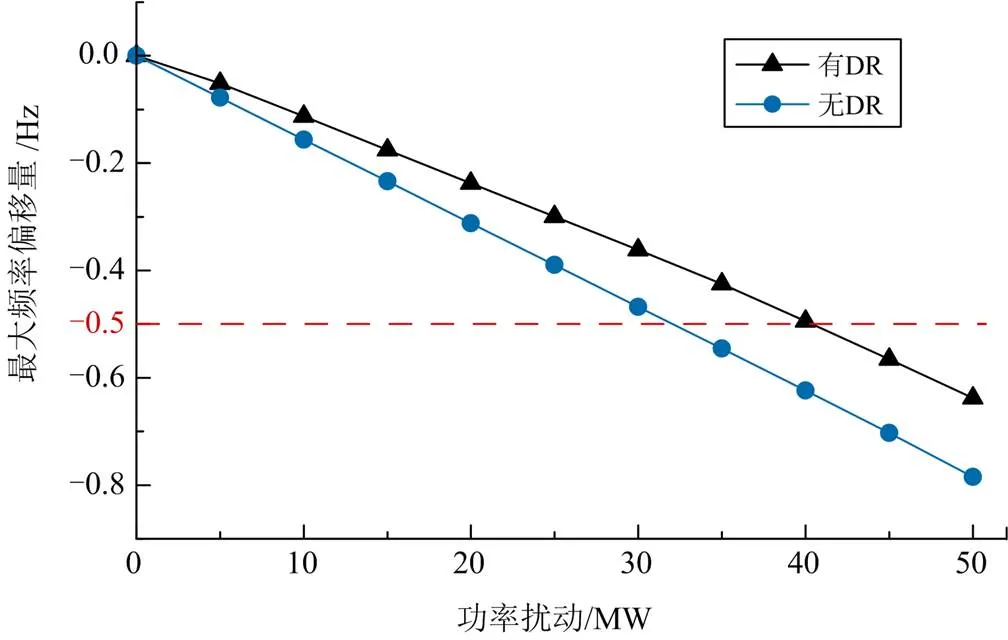
图11 有无DR的最大频率偏移量对比
4.5 不同数据驱动方法转化频率安全约束的效果
本节对比了HDMR与文献[18]中的支持向量机SVM在转换频率安全约束上的表现。两种算法均采用4.2节的数据集,并在Gen Intel(R) Core(TM) i5-1135G7@2.40 GHz、16.0 GB RAM的硬件环境下测试。比较维度包括计算时间、频率最低点均值和成本,对比结果见表4。
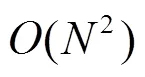

表4 HDMR与SVM对比
在频率最低点和调度成本方面,HDMR方法调度成本是77 931.54美元,平均频率最低点为49.63 Hz;SVM方法调度成本为77 753.17美元,平均频率最低点为49.52 Hz。相比之下,HDMR转换后的频率安全约束更加保守,可充分保证功率扰动后系统频率能够维持在安全范围内。
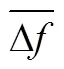
表5 改变时HDMR与SVM方法求解时间对比
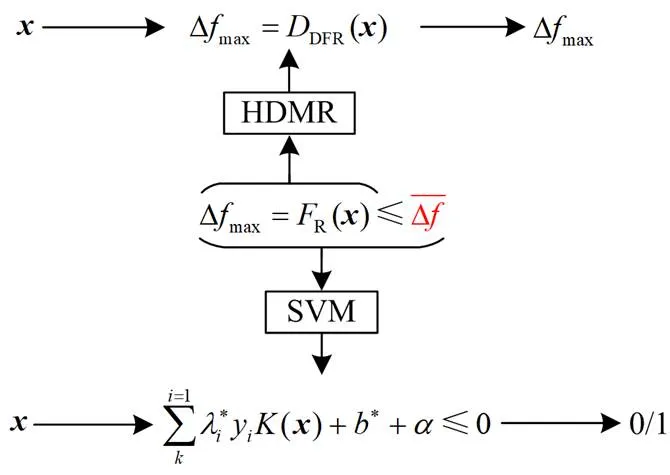
图12 HDMR与SVM转换原理比较
5 结论
新能源占比的不断提高使电力系统惯性下降,满足频率安全约束的最优调度成为新型电力系统亟待考虑的问题。本文提出了考虑需求侧快速响应资源的数据驱动频率约束经济调度方法。首先,将变频空调、储能、电动汽车的频率动态模型纳入系统调频框架。然后,构建考虑频率安全约束的源荷双侧联合经济调度模型。最后,使用基于HDMR的数据驱动方法将复杂高阶非线性约束转化为低阶线性约束并求解。算例结果表明:1) HDMR的计算精度满足调度需求,基于HDMR的数据驱动频率安全约束能够保证经济调度方案在频率指标上的安全性,需求侧快速响应资源参与调频后可以显著提升系统频率韧性;2) HDMR相较于SVM分类器方法,计算效率提升32.36%,转化后的频率安全约束更保守。此外,风险偏好改变时,HDMR方法无须重新训练,适应性更好。
本文所提的数据驱动频率安全约束经济调度方法,为需求侧资源参与新型电力系统的运行支撑提供了安全经济的资源配置工具,也为复杂电力调度优化问题的高效解算提供了一种降阶转化的新思路。
与发电侧调频资源相比,需求侧资源具有强不确定性。在实时性、精准度要求极高的电力系统频率控制过程中,如何通过数据驱动的方法对需求侧资源的不确定性进行建模和处理是下一步需要研究的问题。
[1] 张子扬, 张宁, 杜尔顺, 等. 双高电力系统频率安全问题评述及其应对措施[J]. 中国电机工程学报, 2022, 42(1): 1-25.
ZHANG Ziyang, ZHANG Ning, DU Ershun, et al. Review and countermeasures on frequency security issues of power systems with high shares of renewables and power electronics[J]. Proceedings of the CSEE, 2022, 42(1): 1-25.
[2] 李军徽, 冯喜超, 严干贵, 等. 高风电渗透率下的电力系统调频研究综述[J]. 电力系统保护与控制, 2018, 46(2): 163-170.
LI Junhui, FENG Xichao, YAN Gangui, et al. Survey on frequency regulation technology in high wind penetration power system[J].Power System Protection and Control, 2018, 46(2): 163-170.
[3] 安学民, 孙华东, 张晓涵, 等. 美国得州“2.15”停电事件分析及启示[J]. 中国电机工程学报, 2021, 41(10): 3407-3415, 3666.
AN Xuemin, SUN Huadong, ZHANG Xiaohan, et al. Analysis and lessons of Texas power outage event on February 15, 2021[J]. Proceedings of the CSEE, 2021, 41(10): 3407-3415, 3666.
[4] 王伟胜, 林伟芳, 何国庆, 等. 美国得州2021年大停电事故对我国新能源发展的启示[J]. 中国电机工程学报, 2021, 41(12): 4033-4043.
WANG Weisheng, LIN Weifang, HE Guoqing, et al. Enlightenment of 2021 Texas blackout to the renewable energy development in China[J]. Proceedings of the CSEE, 2021, 41(12): 4033-4043.
[5] National Grid ESO. Interim report into the low frequency demand disconnection (LFDD) following generator trips and frequency excursion on 9 Aug 2019[R]. Great Britain, 2019.
[6] PEARMINE R, SONG Y H, CHEBBO A. Influence of wind turbine behaviour on the primary frequency control of the British transmission grid[J]. IET Renewable Power Generation, 2007, 1(2): 142-150.
[7] AHMADI H, GHASEMI H. Security-constrained unit commitment with linearized system frequency limit constraints[J]. IEEE Transactions on Power Systems, 2014, 29(4): 1536-1545.
[8] PATURET M, MARKOVIC U, DELIKARAOGLOU S, et al. Stochastic unit commitment in low-inertia grids[J]. IEEE Transactions on Power Systems, 2020, 35(5): 3448-3458.
[9] ZHANG Ziyang, DU Ershun, TENG Fei, et al. Modeling frequency dynamics in unit commitment with a high share of renewable energy[J]. IEEE Transactions on Power Systems, 2020, 35(6): 4383-4395.
[10]林恒先, 侯凯元, 陈磊, 等. 高比例风电电力系统考虑频率安全约束的机组组合[J]. 电网技术, 2021, 45(1): 1-13.
LIN Hengxian, HOU Kaiyuan, CHEN Lei, et al. Unit commitment of power system with high proportion of wind power considering frequency safety constraints[J]. Power System Technology, 2021, 45(1): 1-13.
[11]罗金满, 刘丽媛, 刘飘, 等. 考虑源网荷储协调的主动配电网优化调度方法研究[J]. 电力系统保护与控制, 2022, 50(1): 167-173.
LUO Jinman, LIU Liyuan, LIU Piao, et al. An optimal scheduling method for active distribution network considering source network load storage coordination[J]. Power System Protection and Control, 2022, 50(1): 167-173.
[12] YANG Hejun, ZHANG Xinyu, MA Yinghao, et al. Critical peak rebate strategy and application to demand response[J]. Protection and Control of Modern Power Systems, 2021, 6(3): 357-370.
[13] HUI Hongxun, DING Yi, ZHENG Menglian. Equivalent modeling of inverter air conditioners for providing frequency regulation service[J]. IEEE Transactions on Industrial Electronics, 2019, 66(2): 1413-1423.
[14] HUI Hongxun, DING Yi, LIU Weidong, et al. Operating reserve evaluation of aggregated air conditioners[J]. Applied Energy, 2017, 196: 218-228.
[15]王凯丰, 谢丽蓉, 乔颖, 等. 电池储能提高电力系统调频性能分析[J]. 电力系统自动化, 2022, 46(1): 174-181.
WANG Kaifeng, XIE Lirong, QIAO Ying, et al. Analysis on frequency modulation performance of power system improved by battery energy storage[J]. Automation of Electric Power Systems, 2022, 46(1): 174-181.
[16] 鲍谚, 贾利民, 姜久春, 等. 电动汽车移动储能辅助频率控制策略的研究[J]. 电工技术学报, 2015, 30(11): 115-126.
BAO Yan, JIA Limin, JIANG Jiuchun, et al. Research on the control strategy of electric vehicle mobile energy storage in ancillary frequency regulation[J]. Transactions of China Electrotechnical Society, 2015, 30(11): 115-126.
[17]薛禹胜, 赖业宁. 大能源思维与大数据思维的融合(一)大数据与电力大数据[J]. 电力系统自动化, 2016, 40(1): 1-8.
XUE Yusheng, LAI Yening. Integration of macro energy thinking and big data thinking part one big data and power big data[J]. Automation of Electric Power Systems, 2016, 40(1): 1-8.
[18] ZHUANG Xinran, YE Chengjin, DING Yi, et al. Data-driven reserve allocation with frequency security constraint considering inverter air conditioners[J]. IEEE Access, 2019, 7: 120014-120022.
[19] NANDA J, MISHRA S, SAIKIA L. Maiden application of bacterial foraging-based optimization technique in multiarea automatic generation control[J]. IEEE Transactions on Power Systems, 2009, 24(2): 602-609.
[20] BAO Yuqing, LI Yang, WANG Beibei, et al. Demand response for frequency control of multi-area power system[J]. Journal of Modern Power Systems and Clean Energy, 2017, 5(1): 20-29.
[21]陈长青, 李欣然, 张冰玉, 等. 基于多时间尺度的储能调峰调频协同控制策略[J]. 电力系统保护与控制, 2022, 50(5): 94-105.
CHEN Changqing, LI Xinran, ZHANG Bingyu, et al. Energy storage peak and frequency modulation cooperative control strategy based on multi-time-scale[J]. Power System Protection and Control, 2022, 50(5): 94-105.
[22]孙立明, 杨博. 蓄电池/超导混合储能系统非线性鲁棒分数阶控制[J]. 电力系统保护与控制, 2020, 48(22): 76-83.
SUN Liming, YANG Bo. Nonlinear robust fractional- order control of battery/SMES hybrid energy storage systems[J]. Power System Protection and Control, 2020, 48(22): 76-83.
[23] HU Jindi, YE Chengjin, DING Yi, et al. A distributed MPC to exploit reactive power V2G for real-time voltage regulation in distribution networks[J]. IEEE Transactions on Smart Grid, 2022, 13(1): 576-588.
[24] XIE Dunjian, HUI Hongxun, DING Yi, et al. Operating reserve capacity evaluation of aggregated heterogeneous TCLs with price signals[J]. Applied Energy, 2018, 216: 338-347.
[25]赵强, 刘肇旭, 张丽. 对中国低频减载方案制定中若干问题的探讨[J]. 电力系统自动化, 2010, 34(11): 48-53.
ZHAO Qiang, LIU Zhaoxu, ZHANG Li. Discussions on the several problems of under-frequency load shedding scheme in China[J]. Automation of Electric Power Systems, 2010, 34(11): 48-53.
[26]电能质量—电力系统频率偏差: GB/T 15945—2008[S].北京: 中国电力出版社, 2008.
Power quality—frequency deviation for power system: GB/T 15945—2008[S]. Beijing: China Electric Power Press, 2008.
[27]方勇杰. 英国“8·9”停电事故对频率稳定控制技术的启示[J]. 电力系统自动化, 2019, 43(24): 1-7.
FANG Yongjie. Reflections on frequency stability control technology based on the blackout event of 9 August 2019 in UK[J]. Automation of Electric Power Systems, 2019, 43(24): 1-7.
[28] Australian Energy Market Operator. Preliminary report- black system event in South Australia on 28 September 2016[R]. Melbourne, Australia: Australian Energy Market Operation Limited, 2016.
[29]宋梦, 于继来, 李碧君, 等. 高维模型表达技术在N-1有功响应静态安全域中的应用[J]. 电力系统自动化, 2015, 39(1): 164-170.
SONG Meng, YU Jilai, LI Bijun, et al. Application of high dimensional model representation in N-1 active power response steady-state security domain[J]. Automation of Electric Power Systems, 2015, 39(1): 164-170.
[30] SONG Meng, GAO Ciwei, SHAHIDEHPOUR M, et al. Impact of uncertain parameters on TCL power capacity calculation via HDMR for generating power pulses[J]. IEEE Transactions on Smart Grid, 2019, 10(3): 3112-3124.
[31] GOODFELLOW I, BENGI Y, COURVILLE A, et al. Deep learning[M]. London, UK: MIT Press, 2016.
[32] SHERALI H D, ADAMS W P. A reformulation- linearization technique for solving discrete and continuous nonconvex problems[M]. Berlin: Springer, 1998.
[33]曹鹏, 刘敏. 基于改进的整数规划法结合零注入节点的PMU优化配置方法[J]. 电力系统保护与控制, 2021, 49(16): 143-150.
CAO Peng, LIU Min. PMU placement method based on improved integer programming method combined with zero injection buses[J]. Power System Protection and Control, 2021, 49(16): 143-150.
[34] ALVARADO D, MOREIRA A, MORENO R, et al. Transmission network investment with distributed energy resources and distributionally robust security[J]. IEEE Transactions on Power Systems, 2019, 34(6): 5157-5168.
[35] RIPLEY B D. Pattern recognition and neural networks[M]. Cambridge: Cambridge University Press, 2007.
[36] RABITZ H, ALIŞ Ö F. General foundations of high- dimensional model representations[J]. Journal of Mathematical Chemistry, 1999, 25(2): 197-233.
[37] BURGES C J C. A tutorial on support vector machines for pattern recognition[J]. Data Mining and Knowledge Discovery, 1998, 2(2): 121-167.
Data-driven frequency constrained economic dispatch considering fast demand resources
YAO Yu1, YE Chengjin1, ZHU Chao2, DING Yi1, XU Yile3, WANG Lei2
(1. College of Electrical Engineering, Zhejiang University, Hangzhou 310027, China; 2. Economic Research Institute of State Grid Zhejiang Electric Power Co., Ltd., Hangzhou 310008, China; 3. College of Energy Engineering, Zhejiang University, Hangzhou 310027, China)
The frequency of the power system faces challenges with the growing share of renewable energy and the decreasing inertia. It’s urgent to allocate fast demand response resources for frequency regulation.In this paper, the feasibility that inverter air conditions, energy storage and electric vehicles provide frequency regulation reserve is analyzed. A frequency constrained combined economic dispatching model (FCCED) considering the above fast demand response resources is established to uniformly allocate the frequency regulation reserve between generators and loads. Then, a data-driven method based on the high dimensional model representation (HDMR) is proposed to convert the above high-order, nonlinear and implicit frequency security constraint to a low-order and explicit constraint. As a result, the proposed FCCED model can be solved easily. Finally, the modified IEEE 30-bus system validates the effectiveness of the proposed method. It is explained that the proposed frequency security constraint ensures that the abnormal frequency of the system under unbalanced power is within the constraint. And fast demand response resources have an important positive effect on improving the frequency toughness of the system.
fast demand response resources; frequency dynamic model; frequency constrained combined economic dispatching model (FCCED); frequency regulation reserve; high dimensional model representation (HDMR)
10.19783/j.cnki.pspc.220460
国家科技创新2030项目资助(2021ZD0112700);国网浙江省电力有限公司科技项目资助(5211JY220001)
This work is supported by the National Science and Technology Innovation 2030 Project (No. 2021ZD0112700).
2022-03-31;
2022-07-11
姚 宇(1997—),男,硕士研究生,研究方向为电力需求侧管理、数据驱动等;E-mail: zjuyaoyu@zju.edu.cn
叶承晋(1987—),男,通信作者,博士,研究员,研究方向为电力系统规划运行、电力需求侧管理;E-mail: yechenjing@zju.edu.cn
丁 一(1978—),男,博士,教授,研究方向为智能电网、电力系统可靠性。E-mail: yiding@zju.edu.cn
(编辑 姜新丽)

