土石坝对水流渗流过程的影响研究
周 杰
(泗县水利局,安徽 泗县 234300)
1 前言
土石坝在各类蓄水工程中广泛应用。为了能够对土石坝的工作性能有明确认识,许多学者对土石坝工程的坝体及坝基的各类相关力学性质和特点开展了广泛研究,詹美礼等[1]对充填管袋渗流各向异性特征及堤坝管袋堆积体内的应力-渗流相互耦合作用的特征关系进行了研究,研究结果表明:渗流主要沿着管袋间接缝向下游运动,管袋接缝呈现的与渗流方向的位置情况不同,渗透系数大不相同,上覆应力也会对渗透系数产生重要影响,同时影响渗流的各向异性。吴世余等[2]在毛管水存在条件下对由其所产生的对土体强度、土体变形和水在土中的渗流影响作用进行了研究。研究结果表明:粉性土水压传递特征与其较高的毛管水头和较大的渗流系数有直接关系,毛管水的存在将会对此类土修筑的堤坝工程特性产生明显影响。刘晓等[3]针对堤坝渗漏监测数据受到多种因素干扰的问题,通过渗漏地电模型的两组对比试验的结果分析,表明所建立的渗漏地电模型能够优化监测数据,达到对监测数据的正确解译,从而为渗流预警提供帮助。林岳等[4]根据《国际堤坝手册》中介绍的堤坝侵蚀破坏机理,总结分析并对比了国内外用于堤坝设计的各类规范和准则中关于堤坝破坏的准则判断,为我国基建提供了数据支撑。李向阳等[5]对有关土石堤坝渗漏监测问题进行了深入研究,研究结果表明:电场耦合建立的数学模型能够将渗流场与电场同步关联,从而对介质电阻率随渗流场的变化特征进行模拟,据此判断渗透破坏时的特征。由于电流场与渗流场的相似性,戴前伟等[6]通过检测电流场电位差研究迎水面和背水面的渗流特征,从而获得与土坝管涌发生的渗流特征相关参数的变化过程。研究结果表明:矢量电流流场法对于揭示与土石坝渗流相关问题十分有效,为堤坝渗流相关问题的研究提供了新思路。作为一个取水水源水库,青草沙水库在上海市的供水系统中发挥着重要作用,陆忠民等[7]对水库堤坝设计中遇到的多种复杂地质和水文条件进行了安全验证。验证结果表明:该水坝设计具有抗击多种复杂地质水文条件的能力,是一个具有一系列创新成果的堤坝设计。
以上学者虽然针对土石坝渗流中遇到的多种问题开展了深入研究,但是对土石坝的存在条件下,水流在坝体内的渗流运动过程的研究尚未见诸文献中。本文根据一现场实际的土石坝堤坝工程,开展了在水位为设计蓄水水位条件下,坝体内水流渗流运动过程的特点研究,研究中,主要通过数值模拟方法,对其水流的向下游的渗流过程进行模拟计算,用到了Geo-studio 软件中的SEEP 模块。
2 工程概况
某水库大坝控制径流面积50 km2。水库原设计总库容约300×104m3,其中防洪库容25×104m3,兴利库容275×104m3。水库排灌干渠渠道全长11.49 km,灌区对水资源的需求量随经济的不断发展、人民生活水平的提高呈日趋增大的趋势,与现供水能力之间的矛盾更加突出。工程的长期稳定对于灌区用水的稳定供应十分关键,堤坝截面设计形式如见图1,修筑堤坝时,主要通过对碎石土进行逐层压实作业来完成该堤坝工程的修建,组成碎石土的材料主要有:粘土、卵石、砂土、尖棱角碎石,颗粒级配良好,构成碎石土的各类材料的各项物理力学参数如见表1。

表1 土石坝材料物理力学参数
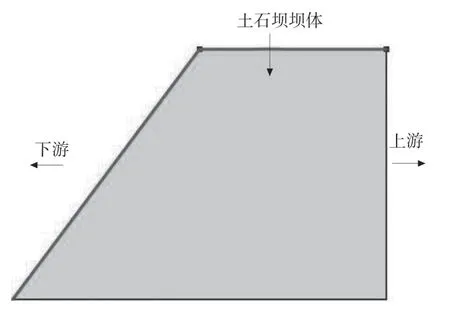
图1 堤坝横断面图
3 数值模拟
3.1 模型的建立
Seep 模块是专门用于水流渗流分析的一个模块,在Geostudio 软件中内置,其中有关水流及其他各种流体的特性,在软件中有各种方法进行设置,最重要的方式是采用软件自带的估算功能对其进行估算后,根据试验获得的数据进行调整,本文即是采用该种方法,经过设置后使其特性与自然条件下水流的流体特性极为近似,以使后续的分析计算更加精确,随后设置堤坝材料的相关物理及力学性质,这主要通过输入材料功能来实现,根据上文表1中的材料参数,设置材料属性,最后赋值给对应区域。
根据图1中的堤坝截面形式,设计相应的堤坝计算模型,该堤坝被构建成与图1一样的直角梯形截面,见图2,右侧为蓄水水库,堤坝的梯形直角边与水库中的水接触,堤坝坝基底宽18 m,9 m 的顶宽9 m,高12 m,坝基梯形截面的自身惯性矩(IY和IZ)大小为9.58×1015m4,安全系数设计为1.5。

图2 计算蓄水水库坝体渗流模型
3.2 渗流特征及总水头变化
经过数值模拟计算,完成后的渗流结果图见图3。总水头随着X 大小的变化过程图见图4。

图3 数值计算的渗流结果图
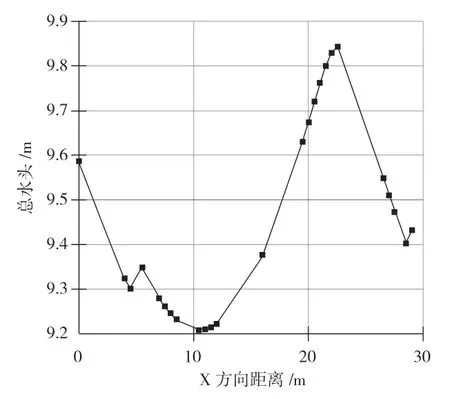
图4 水流总水头随X(距离)的变化图
对于渗流过程,最重要的参数表现特征即为坝体内总水头的分布变化特点,见图3,为最终计算完成后坝体内总水头的梯度云图,由图中可以看出,从右侧开始,总水头向左侧变化,逐渐变小,右侧的总水头为10 m,左侧最小总水头为0 m,这说明坝体发挥了蓄水作用,水头梯度变化逐渐增大,右侧水头变化缓慢,左侧水头变化加速,说明越往左侧,坝体材料的对上游水流的阻碍作用越强。坝体内的总水头呈现出由右上向左下的变化趋势,右上总水头最大,左下端总水头最小。
图4所示为水流在坝体内的总水头随着逐渐远离源头水体的变化趋势图,由图可知,水流的总水头整体呈现出正弦曲线的形式,X=10 m 和X=22 m 处为正弦曲线的拐点也就是极值点,上游总水头约为9.6 m,随着X 的增大先逐渐变小,减小到X=10 m位置处的9.2 m,接着随着X的增大又逐渐增大,达到X=22 m 处的9.85 m 总水头后不再上升,而又逐渐减小,最终减小至值约为9.4 m 的总水头值。
4 结论
本文通过数值模拟手段,对重力式土石坝设计的安全性和稳定性进行了计算分析,主要获得以下结论:
(1)坝体内的总水头呈现出由右上向左下的变化趋势,右上总水头最大,约为10 m,左下端总水头最小,值为0 m。
(2)随着逐渐远离源头水体,在同一高度(蓄水水位的同一深度)处,水流的总水头整体呈现出正弦曲线的形式。
(3)经过计算,该坝体设计断面形式合理,起到了良好的蓄水作用,可为类似工程提供参考。

