基于IPSO-BP的空气质量指数预测
胡 青,胡 珍,曲 润,龚世才
(1.浙江科技学院 理学院,杭州 310000;2.湖北工业大学 理学院,武汉 430068)
随着我国经济的快速发展以及城市化进程的不断加快,空气污染问题变得愈发严峻.对人体健康也产生了极大危害[1].空气质量指数(AQI)作为衡量空气质量的重要指标,其大小反映了空气污染的水平.因此,利用科学的方法预测AQI,对居民健康出行及城市环境治理有着重要的指导意义.
针对空气污染方面的预测,传统的AQI预测模型有时间序列模型、线性回归模型、灰色预测模型等[2].但在空气质量预测体系中,各影响因素间有着较强的非线性关系,利用传统统计预测模型预测AQI得到的精度较低.由于神经网络模型具有较强的非线性拟合能力,可以较好地完成对AQI的预测.艾洪福等[3]利用BP神经网络对空气质量进行预测,相较于传统预测方法提升了预测精度.但是单一BP神经网络收敛速度慢且易陷入局部最优解.为了进一步提高预测精度,相关学者利用优化算法对BP神经网络进行改进并应用到AQI预测中.蒋奇峰等[4]利用量子粒子群算法(QPSO)对径向基神经网络(RBF)进行改进,提升了神经网络的收敛速度及稳定性,并在AQI预测中取得较好效果.
综上所述,传统的单一BP神经网络AQI预测效果较差,尽管有些学者利用优化算法对神经网络进行改进,在一定程度上提高了模型的预测精度,但在迭代后期算法仍存在易陷入局部最优、收敛速度慢的缺陷,影响了预测效率.
为解决上述问题,本文利用改进的粒子群算法对BP神经网络的权值和阈值进行优化,得到预测精度高、全局搜索能力强的IPSO-BP模型.使用改进后的模型对杭州市空气质量指数值进行预测,实验结果表明,该模型在预测精度及拟合优度方面相较于其他模型显著提升,能够很好地应用于实际的AQI预测中.
1 相关算法理论
1.1 BP神经网络原理
BP神经网络是一种采用误差反向传播算法进行学习的多层前馈网络[5],其结构包括输入层、隐含层、输出层.BP神经网络的拓扑结构如图1所示.

图1 BP神经网络结构
1.2 粒子群优化算法
粒子群优化算法是一种受到生物种群行为特征启发的算法[6],算法的粒子通过迭代进行寻优求解.其中每个粒子都有速度V和位置X两个属性,X代表粒子移动的快慢,V代表粒子移动的方向.位置和速度的迭代更新公式如下:
(1)
(2)
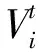
2 改进的粒子群优化算法
2.1 混沌映射初始化种群
粒子群算法对种群进行初始化时,采用的是随机生成的方式,这种方式会使得种群分布不均匀,影响后期的迭代寻优.为了提高算法全局搜索能力,避免迭代后期种群多样性降低,同时考虑到混沌映射具有随机性、遍历性和规律性等特点[7],利用混沌序列对种群进行初始化.汤安迪等[8]证明了Tent映射的均匀性及遍历性优于经典的Logistic映射,故本文采用Tent映射完成种群的初始化.Tent映射公式如下:
(3)
其中:k为映射次数,xk为第k次映射函数值.
Tent映射初始化种群的步骤如下:
步骤1:设置种群规模N、维数d,初始值x0
步骤2:按照式(3)将粒子所在位置xi的每一维xik(k=1,…,n)映射到[0,1]区间上
(4)
其中:xlb、xub为粒子位置所处维度的上下边界.
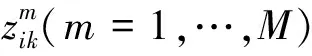
(5)
步骤4:按照式(5)将混沌序列中的点映射回原空间
步骤5:xi经过Tent映射后的产生的混沌序列:
假设种群规模为100,在二维搜索空间中产生的初始化种群分布图见图2.从图中可以看出,相比随机初始化的种群序列,通过Tent映射混沌序列产生的初始种群分布更加均匀,遍历性更好.

图2 初始化种群分布图
2.2 自适应惯性权重法
惯性权重因子ω具有影响算法寻优能力的作用,即当ω取值偏小时,全局搜索能力随之降低,算法易形成局部最优解;当ω取值较大时,收敛能力随之变差,导致算法无法形成最优解而陷入无限寻优的情况.为解决参数ω的寻优能力局限性问题,引入了自适应惯性权重法.该方法可以自行调整ω迭代时的变化速率,以提高其寻优效率,公式表示如下:
(6)
其中:ωi为第i个粒子惯性权重,ωmin和ωmax是预设的最小与最大惯性系数,本文中ωmin取0.4,wmax取0.9,fi为第i个粒子的当前迭代适应度值,favg为粒子的平均适应度值.
2.3 高斯扰动策略
高斯分布在局部空间搜索性能好,对全局最优个体使用高斯扰动策略[9]有利于算法跳出局部极值点,同时也增强了算法全局搜索性能.使用高斯扰动策略生成新个体的公式如下:
(7)
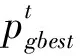
2.4 算法性能测试
2.4.1 算法初始化参数设置
为了验证IPSO的寻优效果与稳定性,本文选取遗传算法(Genetic Algorithm,GA)、粒子群算法(Particle Swarm Optimization,PSO)、IPSO进行寻优结果的对比,通过上述Tent映射的边界值处理公式将种群中所有个体的取值范围统一为[0,1].其中所有算法的种群数量设置为30,最大迭代次数为1 000.
2.4.2 测试函数选取
为了进一步验证IPSO的寻优性能,采用4个具有不同特征的基准测试函数进行测试.其中,F1、F2是单峰函数,F3、F4是多峰函数,测试函数维度为30,寻优的最优值为0,4个基准测试函数及其具体信息如表1所示.

表1 基准测试函数
2.4.3 算法寻优能力分析
为了去除偶然性带来的误差,分别利用上述3种算法对4个测试函数进行30次独立试验,测试函数的寻优结果见表2.
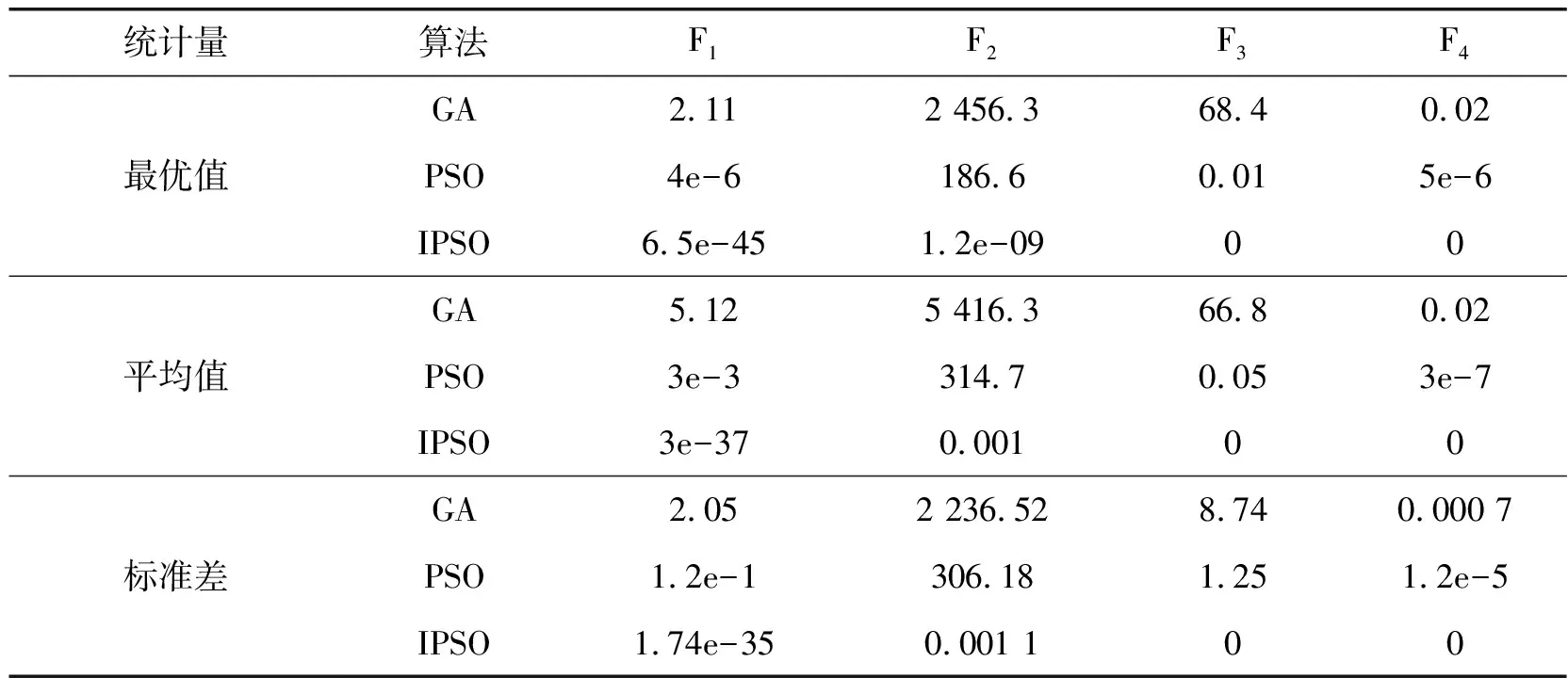
表2 测试函数寻优结果
由表2可知,IPSO对于单峰函数F1、F2的优化效果非常明显,其寻优的指标值远超其他算法;对于多峰函数F3、F4,IPSO最优值均为0,寻优效果优于GA与PSO.不论是单峰函数还是多峰函数,IPSO在多次寻优的过程中,平均值和标准差均比其他算法更小.表明IPSO的稳定性和鲁棒性明显优于其他算法,IPSO拥有更好的全局寻优及局部搜索能力.
2.4.4 算法收敛性分析
通过对基准测试函数迭代进化曲线的绘制,可进一步对比分析各个算法的收敛性及其局部空间解的搜索能力,从而更加精准地评判其预测性能,图3-图6为所有算法迭代1 000次后的进化曲线图.

图3 F1进化曲线
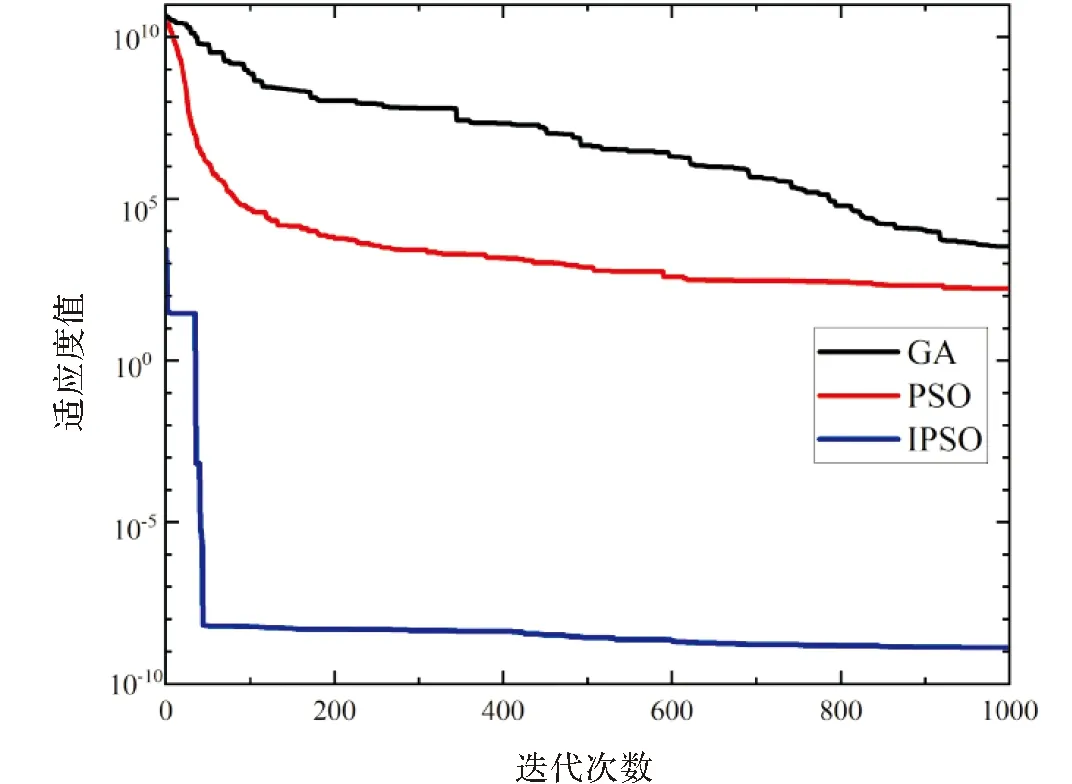
图4 F2进化曲线

图5 F3进化曲线
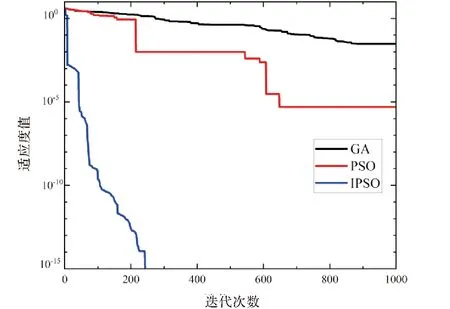
图6 F4进化曲线
由图3—图6可知,相比较其他几种算法,IPSO迭代更少次数进入相同精度,表明引入的Tent映射提高了初始解的质量,使得种群分布更加均匀,从而提高了算法的收敛速度.当算法的寻优值存在不同程度的停滞时,IPSO的寻优值呈现出波动下降.表明优化策略对算法的改进使得算法有能力跳出局部极值,提升了算法的全局搜索能力.
3 仿真研究
3.1 模型预测结构
IPSO-BP模型主要思想是利用改进后的粒子群算法取代梯度下降法在全局范围内对BP神经网络中的权值和阈值进行大范围搜索,通过适应度值的更新不断调整训练误差,迭代完成后通过解码形成最优权值及阈值.同时结合改进后算法收敛速度快、泛化能力强的特点对BP神经网络进行训练,最后得到预测性能更好的神经网络模型.模型的流程图见图7.

图7 基于IPSO-BP的空气质量预测模型流程图
3.2 数据采集及预处理
本文数据是从中国空气质量在线监测分析平台实时监测的杭州市空气质量数据中获取的,采样时间为2020年10月1日至2021年9月15日,共计300组样本数据.训练集为随机选取的270组数据,测试集为剩余30组数据.其中的6组变量分别为PM2.5、PM10、SO2、CO、NO2、O3.
由于数据的单位或数量级的不同,可能导致收敛速度变慢、训练时间变长等问题.因此,要对样本数据进行归一化处理,归一化公式如下:
(8)
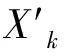
3.3 BP神经网络结构
BP神经网络结构包括输入层、输出层以及隐含层三个部分.其中,输入层为6个节点(提取的4个主成分),输出层为1个节点(AQI),隐含层节点数是决定BP神经网络预测精度的重要因素[10],通常神经网络中确定隐含层中神经元数量可以使用经验公式(9)进行计算.
(9)
其中:q为隐含层的节点个数,m为输入层的节点个数,n为输出层的节点个数,a为1至10之间的常数.
通过不断改变隐含层神经元数目,并代入神经网络训练,得到在不同隐含层神经元个数下的均方误差(表3).

表3 隐含层节点个数对应的均方误差
由表3可知,当均方误差最小时,隐含层对应的节点数为8.因此,本文隐含层节点个数为8.由此可得训练的网络结构为6-8-1.
3.4 结果分析
将数据分别带入各自模型中进行训练,得到的仿真预测结果如图8所示.
由仿真结果可知,IPSO-BP模型的预测曲线的拟合程度高于GA-BP、PSO-BP以及BP模型,预测值更加接近真实值.因此,IPSO-BP模型对AQI的预测更加精准.
为了对所建立的空气预测模型的性能进行全面而系统的分析,本文选取均方根误差(RMSE)、均值绝对误差(MAE)、平均绝对百分比误差(MAPE)、拟合优度(R2)作为模型优越性的衡量指标.计算公式如下:
(10)
(11)
(12)
(13)
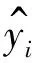
利用训练好的模型测试AQI,得到4种模型的性能评价结果见表4.

表4 预测模型性能评价结果
由表4可以得出,经过相关算法优化后的组合模型的预测效果明显优于单一的BP神经网络模型.其中,在组合模型中,相比较GA-BP、PSO-BP模型,IPSO-BP模型的RMSE、MAE、MAPE数值最小,决定系数R2为0.984,最接近1,拟合程度最优.因此,本文提出的IPSO-BP模型的预测精度最好,预测误差最小.能够有效地应用于空气质量指数的预测中.
4 结语
本文提出了一种改进的粒子群算法(IPSO),并基于BP神经网络构建了AQI预测模型(IPSO-BP).通过改进后的粒子群算法来优化BP神经网络权值及阈值,与未优化BP神经网络相比,显著提升了其预测精度及拟合优度,可有效预测AQI.下一步研究重点是将IPSO-BP模型应用到实际工程领域中,以进一步验证其性能.

