基于改进Richards法的港珠澳大桥沉管隧道沉降预测研究

张雨雷，孔令臣，刘思国，李雨润，纪文利

（1.中交第一航务工程局有限公司，天津 300461；2.中交天津港湾工程研究院有限公司，天津 300222；3.天津市水下隧道建设与运维技术企业重点实验室，天津 300461；4.中交天津港湾工程设计院有限公司，天津 300461；5.河北工业大学土木与交通学院，天津300401）

0 引言

虽然沉管隧道工法在我国起步较晚，但是发展非常迅速。在我国第一条广州珠江隧道建成通车不足30 a的时间里，先后建成20余条沉管隧道。由于早期沉管隧道抗浮系数为1.1～1.2，人们很少考虑沉降问题，但是绝大多数沉管隧道都会出现不同程度的沉降，特别是对于软土地基上的沉管隧道沉降值甚至可以达到几十厘米，如：上海外环沉管隧道最大沉降为310 mm[1]。

在土木工程领域中对基础沉降计算有数百年的历史，涌现出了非常多的预测模型，尽管已建成的沉管隧道的数量不少，但国内外关于沉管隧道沉降的研究却十分有限。孙钧院士提出对于港珠澳大桥沉管隧道工后沉降需要长期连续观测的要求[2]，沉管隧道管节沉降是沉管安全的不利因素，也是沉管隧道建设中无法避免又必须关注的安全问题。不均匀沉降过大会造成管节脱离、管内涌水，进而引发安全事故。传统的沉降预测模型在上部荷载维持相对稳定或者已知最终荷载情况下进行。同时，陆上工程的地基参数获取条件较好，具有较明确的获取方式，而海上工程获取原状土较为困难，高昂的费用也是影响获取沉降模型相关物理力学参量的重要因素。

国内对于沉管沉降的大部分研究集中于潮汐对沉降的影响，而考虑管顶回淤影响的研究较少，魏纲等[3]通过理论计算得出潮汐影响下甬江隧道沉管段的浮动范围为4～8 mm，不同管节的同一位置截面中，越靠近隧道中点的浮动量越大。谢雄耀等[4]通过有限元计算得出了淤积对隧道长期沉降影响显著，同时指出隧道随潮位变化产生周期性浮动，且不转化为永久沉降。

本文结合港珠澳大桥工程实例，沉降测点布置情况[5]，通过对双曲线法、星野法、费尔哈斯法[6]、Richards生长曲线法[7]、支持向量机（SVM）[8]、差分整合移动自回归（ARIMA）[9]和基于遗传算法优化的神经网络（GA+BP）[10]7种常用预测模型进行适用性研究，同时通过BP神经网络以及首次提出的改进Richards法，进行考虑回淤及清淤影响的沉管隧道沉降预测研究，本研究不仅对港珠澳大桥沉管隧道的安全运营提供了极大助益，也为今后沉管隧道的设计施工提供宝贵经验。

1 工程概况

港珠澳大桥主体工程跨越伶仃洋外海，全长近55 km，沉管隧道总长6.7 km，沉管段长5.664 km[11]。

结合工程地质实况，沉管隧道区域主体采用2种地基处理方式，人工岛暗埋段的地基经降水联合堆载预压后采用高压旋喷改良地基；沉管隧道E1S3—E5和E30—E33S6采用挤密砂桩方案[12]，其中部分区域采用挤密砂桩+堆载预压进行地基处理。沉管隧道E6—E29采用天然地基基础方案。管节横断面图如图1所示。

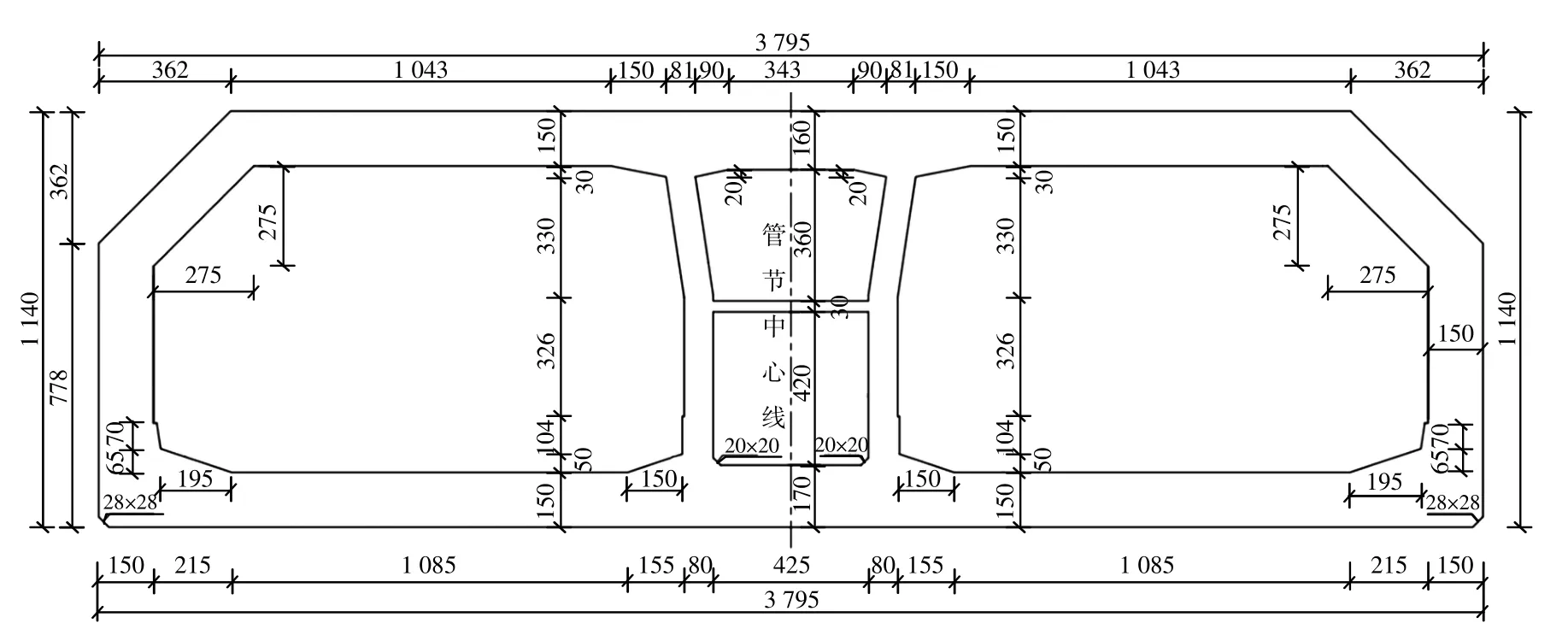
图1 港珠澳大桥沉管隧道横断面图（cm）Fig.1 Cross-section of Hongkong-Zhuhai-Macao Bridge immersed tunnel(cm)

对港珠澳大桥沉管沉放后进行了19次回淤扫测，管顶回淤量如图2所示。从图中可看出管顶回淤量近似线性增长的规律，对E21管顶回淤高度进行线性拟合，其相关系数为0.997。本文中使用的回淤时间序列通过对图2管顶回淤高度进行曲线拟合获取。选取其中回淤量最明显的E21管节与回淤量不明显的E7管节进行沉降预测研究。

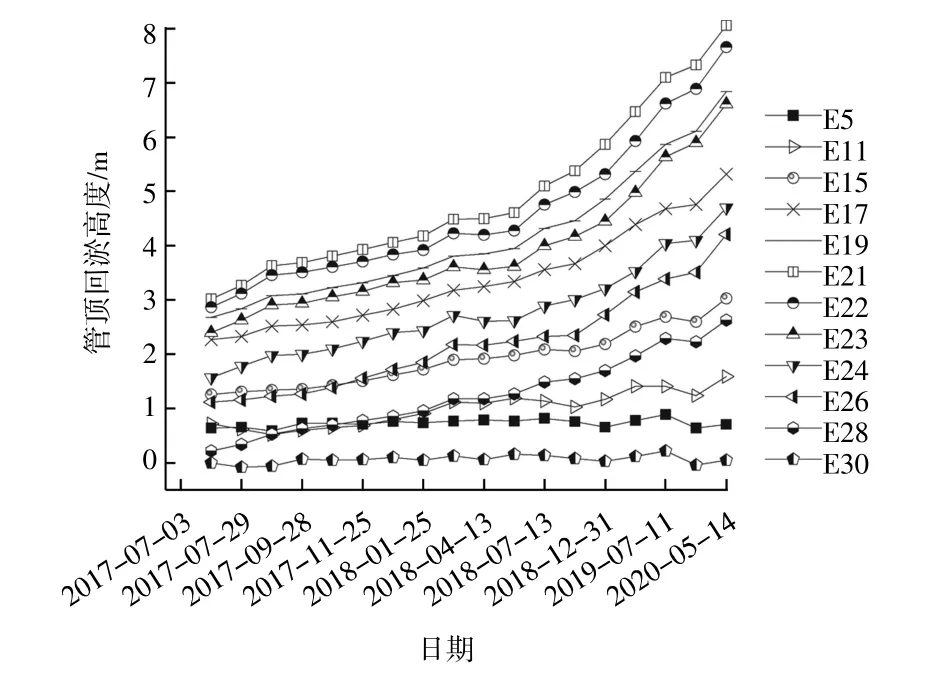
图2 管顶回淤量扫测统计Fig.2 Survey and statistics of back siltation at tube top

2 模型对比分析

对于双曲线法、星野法、费尔哈斯法、Richards生长曲线法，其中yt表示t时刻的沉降量，y0表示初始时刻的沉降量，A、B、C、D为模型待定参数。

双曲线法：

星野法：

费尔哈斯法：

Richards生长曲线法：

对于ARIMA模型，通过对ACF检验与PACF检验对模型进行识别，差分进行定阶，BIC准则进行参数估计，并对模型进行白噪声与模型质量检验。

对于SVM模型预测需要提供预估的预测值进行，因此，较适用于具有周期性规律的数据，本次提供预估值为拟合模型使用沉降数据的最大值。

对于GA+BP模型，通过遗传算法优化BP神经网络的权重与阈值，提高模型收敛速度，避免陷入局部最优解。

通过E7管节2 a的实测数据进行模型的建立，计算全部实测数据与预测数据的相关系数（见表1），并将预测结果与实测数据绘制于图3中。

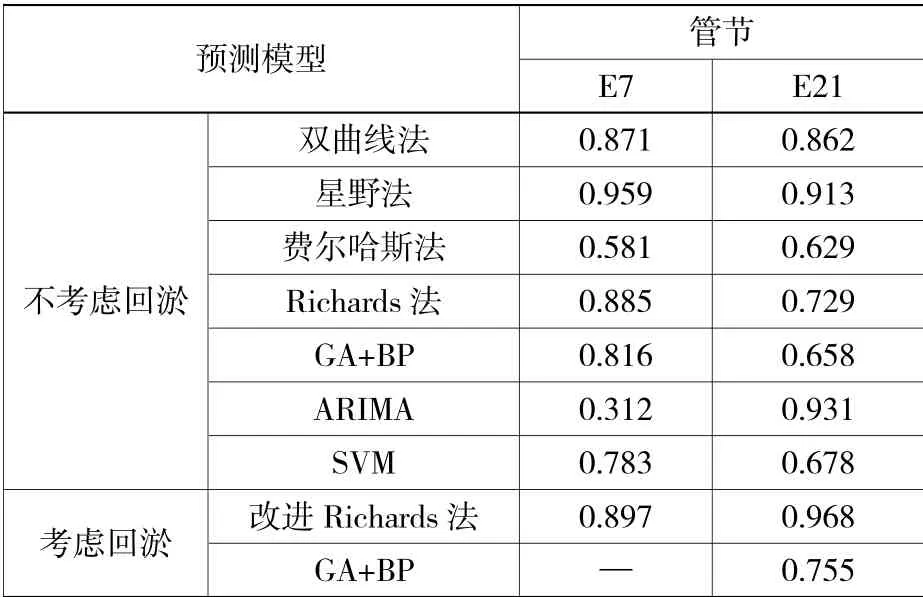
表1 预测模型相关系数汇总表Table 1 Summary of correlation coefficients of prediction model

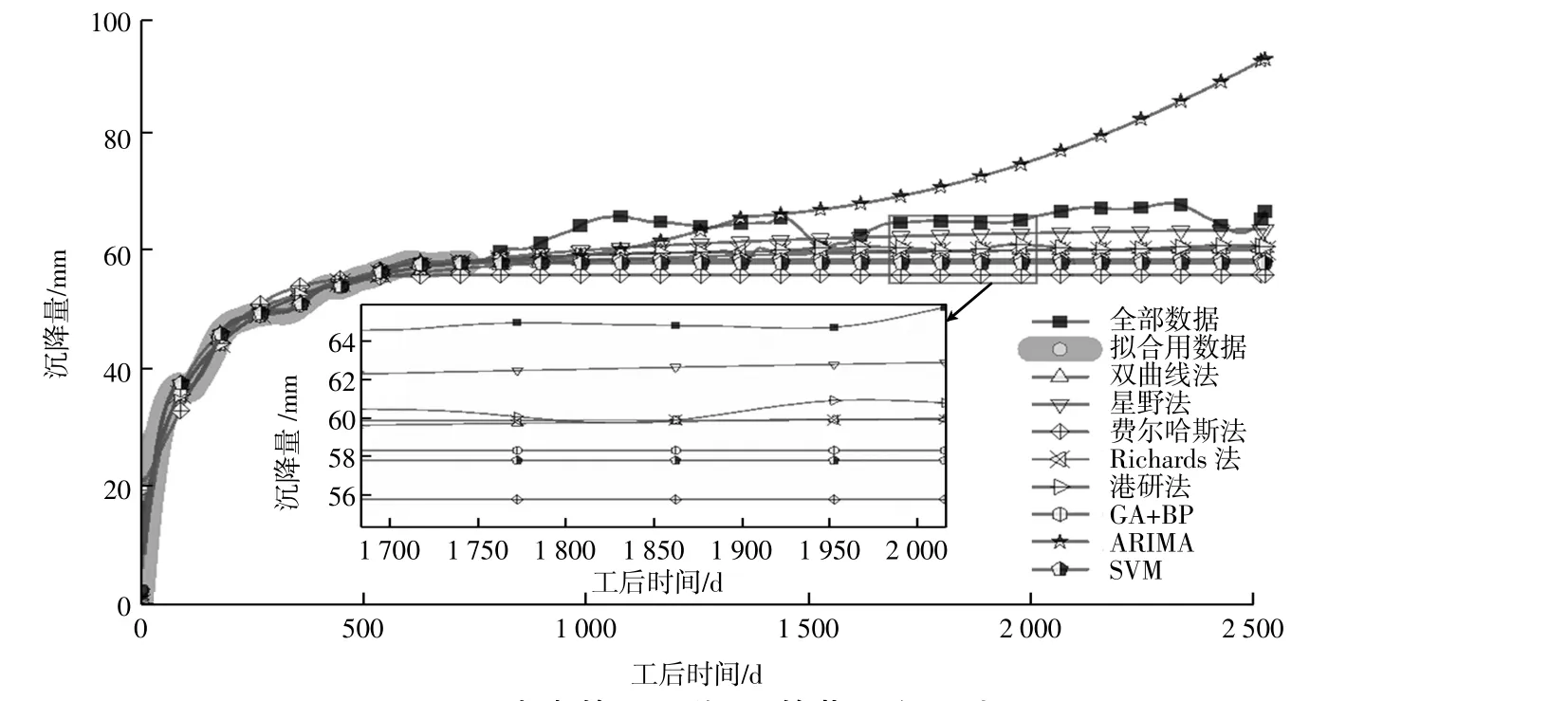
图3 不考虑管顶回淤E7管节沉降预测Fig.3 Settlement prediction of E7 tube segment without considering back siltation at the top of the immersed tunnel

由图3看出曲线拟合状况良好，预测结果除ARIMA模型未收敛外，其余模型收敛程度相似。对于E7管节模型预测质量由高到低分别是星野法＞Richards法＞双曲线法＞GA+BP＞SVM＞费尔哈斯法＞ARIMA。因此，对于E7管节在不考虑回淤量对沉管沉降影响时，星野法、Richards法、双曲线法和GA+BP全部实测数据与预测数据相关系数均大于0.8，预测质量良好。当考虑回淤量时，改进Richards法较Richards法预测相关系数提高了0.014。

通过对E21管节2 a实测数据进行模型的建立，并将预测值与实测值绘制于图4中。

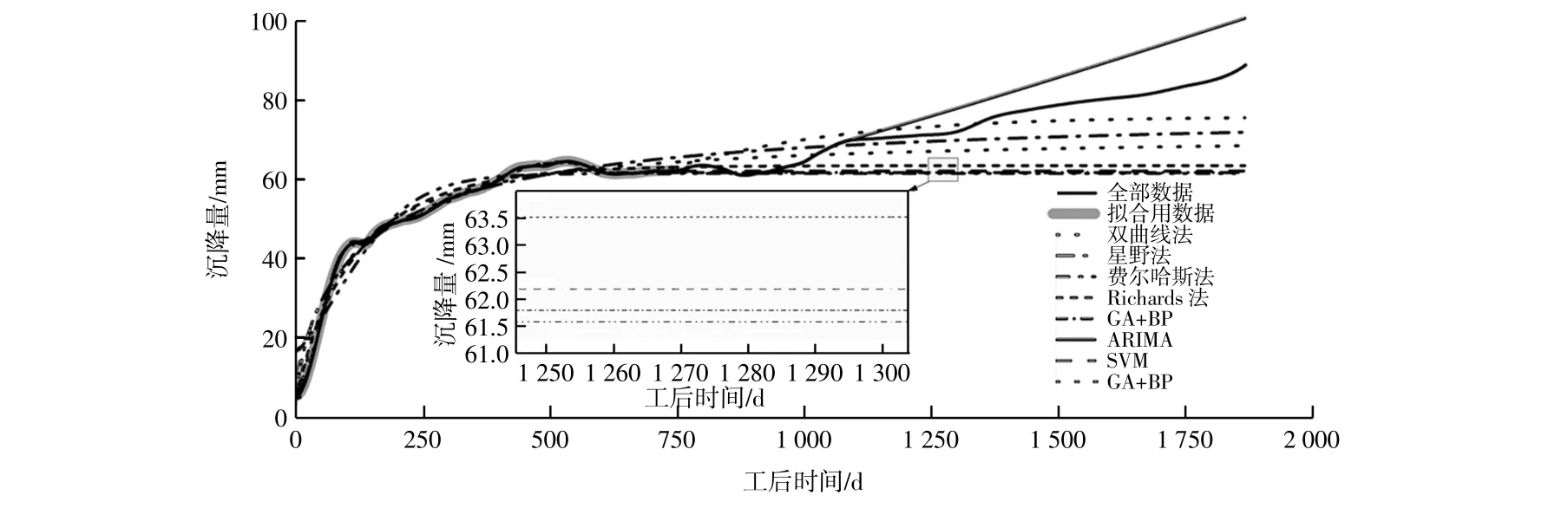
图4 不考虑管顶回淤E21管节沉降预测Fig.4 Settlement prediction of E21 tube segment without considering back siltation at the top of the immersed tunnel

图4显示不考虑回淤情况下，曲线拟合质量欠佳，预测结果除ARIMA模型未收敛外，其余模型收敛程度相似，计算全部实测数据与预测数据的相关系数（见表1）。虽然ARIMA模型相关系数为0.931，但是不同预测时间段的相关系数较低（1 a相关系数0.543、3 a相关系数0.372），同时，结合上面的分析与图3可知，ARIMA模型长期预测失真，因此在模型质量排序中将其剔除后，对于E21管节模型预测质量由高到低分别是星野法＞双曲线法＞Richards法＞SVM＞GA+BP＞费尔哈斯法。对于E21管节在不考虑回淤量对沉管沉降影响时，星野法、Richards法、双曲线法和GA+BP的全部实测数据与预测数据的相关系数均大于0.8，预测质量良好。当将回淤量考虑进预测时，改进Richards法相较于Richards法预测相关系数提高了0.239。

3 考虑管顶回淤的预测模型

通过Fitzhugh H A[13]对Richards模型的分析可知，Richards模型具有单调递增、有界和“S”形的特性，并且对参数m取特征值，Richards模型可以转换为诸多典型的“S”形生长模型，方程拥有很强的灵活性，可以反映规律性的实际增长趋势。由表2可以看出，在管顶回淤高度较大时，通过Richards计算得出的最终沉降量已经超出了魏纲[14]统计国内外19条沉管隧道实测数据得出的总沉降平均值108 mm，参数失真。

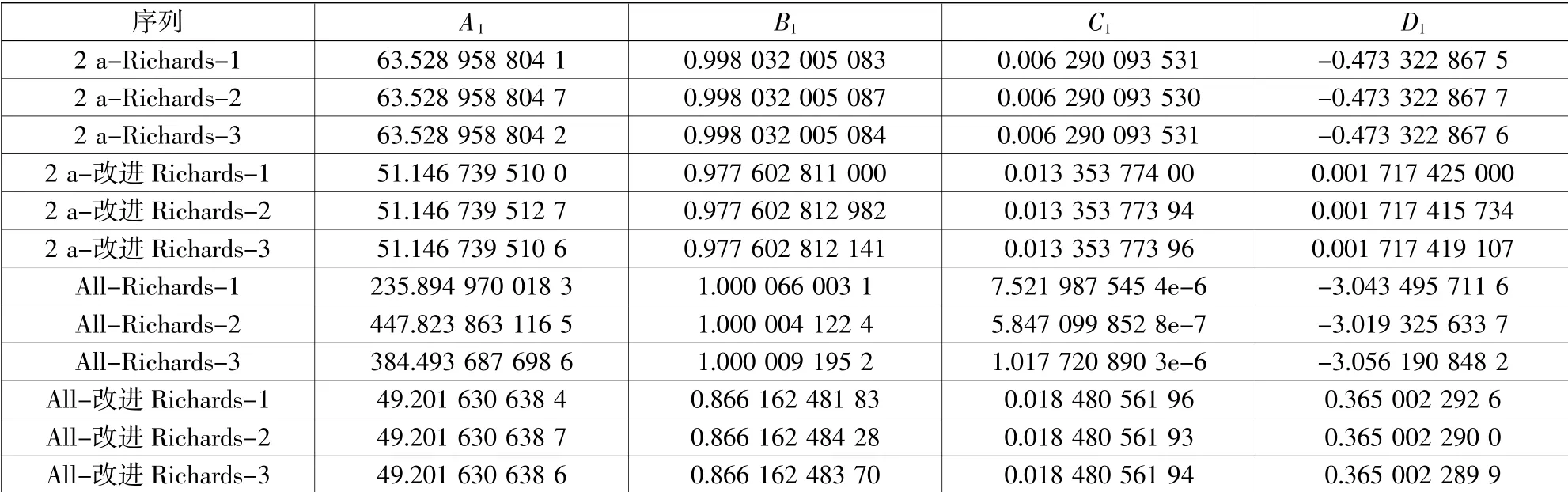
表2 Richards法与改进Richards法参数对比统计表Table 2 Statistical table of parameters comparison between Richards method and improved Richards method

通过对沉管隧道沉降现象及规律进行总结归纳，探讨沉降的组成及机理，结合现有数据，发现回淤量对沉降预测影响较大。因此，考虑通过引入回淤荷载，优化Richards预测结果，由此提出改进Richards法：

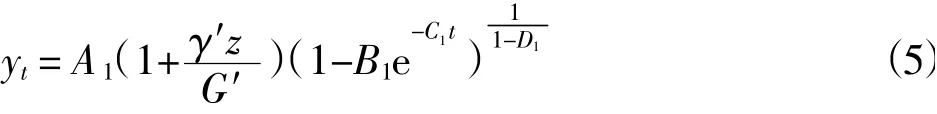
式中：γ′为淤泥浮容重；z为t时刻回淤厚度；G′为管体单宽浮重度；A1为沉管隧道最终沉降量；B1为初始沉降参数；C1为沉降速度参数；D1为曲线形状参数。上面的4个待定参数与Richards法一致，其中A1为去除回淤影响后的最终沉降量。

对E21管节进行考虑回淤预测模型研究，研究通过GA+BP、改进Richards法进行对比（见图5），图5给出了1 a、2 a、3 a的GA+BP和改进Richards法的计算结果，通过曲线可以看出，改进Richards法收敛速度快，1 a的数据即可有较好的计算结果，而GA+BP需要3 a以上的数据才能保证预测精度。表1中呈现2 a二者平均相关系数，改进Richards法高达0.968，而GA+BP为0.755。

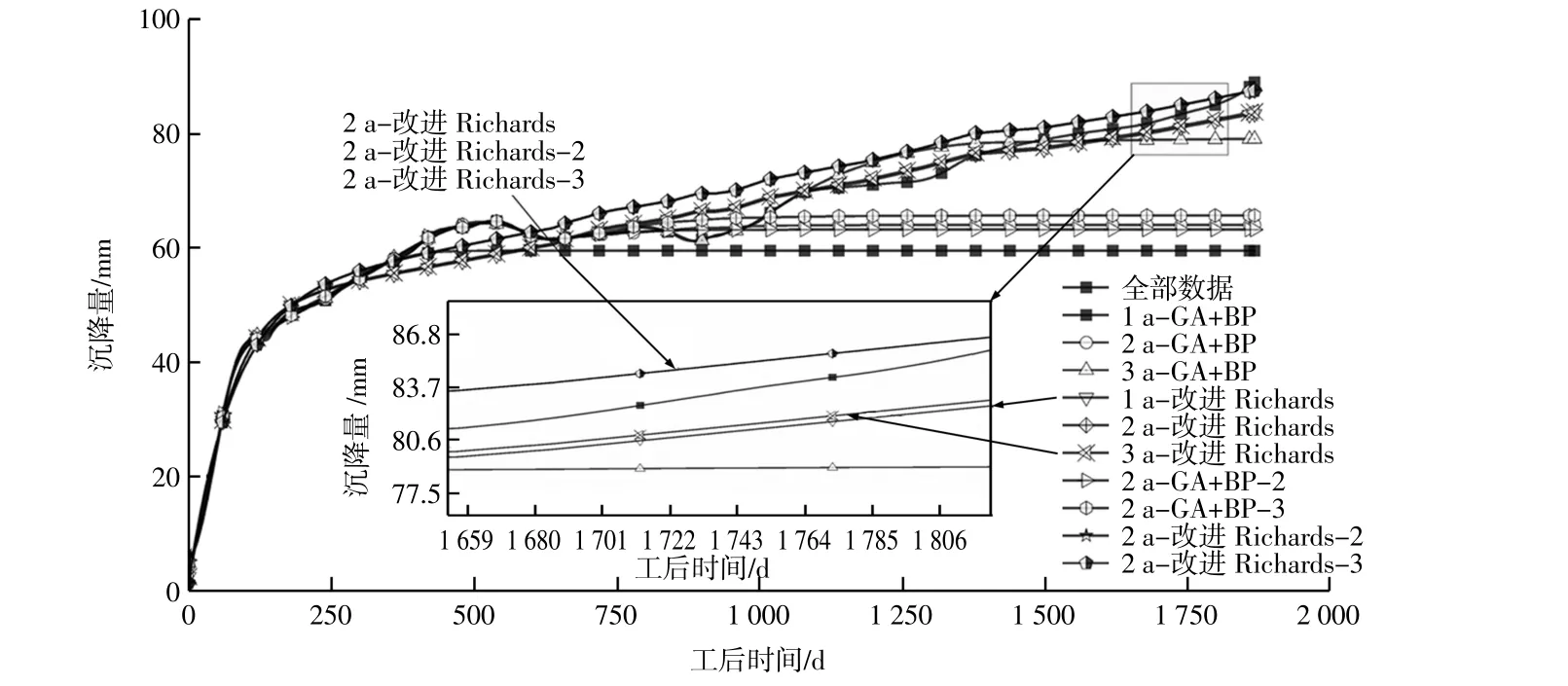
图5 考虑管顶回淤E21管节沉降预测Fig.5 Settlement prediction of E21 tube segment considering back siltation at the top of the immersed tunnel

此外，对模型稳定性进行研究，对于既定工程，改进Richards模型中γ′、G′为常数，因此，待定系数仅为A1、B1、C1、D1与Richards模型一致。表2给出了2 a以及1 872 d的全部实测数据的参数估计结果，通过此表可以看出，二者的2 a参数估计结果均较为稳定，但是对于全部实测数据参数估计结果改进Richards比Richards更稳定，同时，2 a与全部数据改进Richards参数A1沉管隧道最终沉降量估计值的变化量小于4%。

4 清淤预测尝试

改进Richards法通过引入随时间增长的回淤变量来考虑回淤的影响，实际工程中管顶淤积不可能无限增长，可能存在冲刷或者为了降低沉降量而采取的清淤措施。本文通过调整管顶回淤高度，实现清淤预测的尝试。

4.1 港珠澳大桥沉管隧道

对于港珠澳大桥沉管隧道清淤预测选取E21管节进行分析，假定当管顶淤积高度达到5 m时，开始清淤至管顶淤积高度为3 m，如此反复。预测结果见图6。

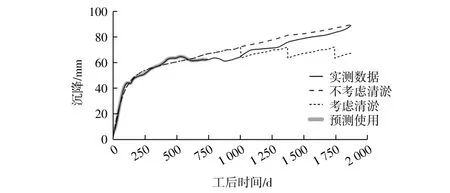
图6 E21管节考虑清淤的沉降预测Fig.6 Settlement prediction of E21 tube segment considering dredging

4.2 甬江沉管隧道

选取甬江沉管隧道E5管节进行分析，通过文献[4]中甬江隧道信息、实测数据、清淤时间及清淤施工标准，结合文献[15]、[16]综合确定回淤速率，预测结果见图7。

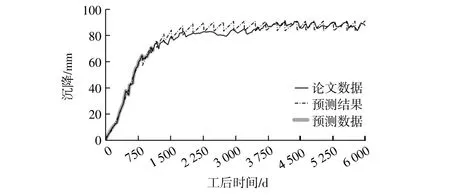
图7 E5管节考虑清淤的沉降预测Fig.7 Settlement prediction of E5 tube segment considering dredging

5 结语

基于港珠澳大桥沉管隧道实测沉降数据，对比研究已有的7种沉降预测算法，提出改进Richards预测模型，主要研究结果如下：

1）在基本没有回淤影响的情况下，沉管隧道沉降星野法、Richards法、双曲线法、GA+BP的相关系数均大于0.8，有较好的预测质量。

2）改进Richards比Richards、GA+BP模型表现得更稳定可靠且收敛速度更快。

3）尝试改进Richards在港珠澳大桥沉管隧道及甬江隧道清淤下的沉降预测，模型表现良好。