基于状态空间线性变换的主动配电网分布式电压控制

杨 鹏，赵子珩，王中冠，安佳坤，杨书强，李 鹏

（1. 国网河北省电力有限公司，河北石家庄 050000；2. 国网河北省电力有限公司经济技术研究院，河北石家庄 050000；3. 天津大学智能电网教育部重点实验室，天津 300072）

0 引言

以光伏为代表的分布式发电以集群化形式接入主动配电网，给配电网安全稳定运行、供电可靠性带来挑战［1］。馈线末端接入的分布式发电改变了配电网传统单一的潮流方向，导致馈线末端电压抬升，影响用电设备寿命的同时造成分布式发电脱网风险［2-3］。渗透率的逐渐提升带来的消纳和网损问题驱动着主动配电网的高效管理和电压控制方法革新［4-8］。

分布式控制更适合含高比例分布式发电的主动配电网电压控制［9］。由于避免了集中模型维护和优化求解，且采用反馈优化控制模式，分布式控制对状态波动具有更快的响应速度。文献［10］和文献［11］基于交替方向乘子法实现了分布式光伏集群的无功电压控制。为应对配电网通信不完备的情况，部分文献讨论了只利用本地量测可获取的信息进行电压控制的方法［12-14］。但文献［15-17］的研究表明，缺乏协调的本地电压控制将引起有载调容变压器（on-load tap changer，OLTC）等设备频繁的档位变化，从而对设备寿命造成影响，更不利于配电网的经济运行。文献［18］提出了采用分段线性下垂电压控制的策略，但没有充分利用分布式光伏的无功调节能力。文献［19］提出了基于延迟下垂策略的电压控制方法，然而对延迟系数的选择并未给出行之有效的方案。分布式控制的方法平衡了系统的稳定性和最优性，但并未考虑分布式光伏的无功可调范围，严重限制了其实用价值［20-21］。

对于分布式发电广泛接入的中低压配电网而言，其电压控制的挑战还在于调度中心往往不掌握其精确的模型参数，对分布式电压控制效果及收敛速度造成不良影响。为解决上述问题，本文提出一种基于历史量测数据进行状态空间线性变换的方法，从而实现电压控制模型的高维线性化等值。目前已有相关数据驱动方法用于潮流计算。文献［22］通过构建状态空间形式，得到与节点注入功率的线性映射关系，通过历史测量数据回归得到线性潮流关系。文献［23］则通过人工神经网络得到潮流计算的映射关系，但上述方法脱离模型支撑，精度效果有限。根据空间变换理论，低维空间下的非线性模型，可通过升维映射在高维空间中转换为线性方程而不失精确性。本文基于Koopman 升维方法［24-26］，利用历史数据样本，训练得到高维电压-无功线性方程，并以此推导分布式牛顿法的精确迭代方向，实现不依赖模型参数的分布式电压控制。

1 主动配电网电压控制模型

1.1 基于线性化Distflow模型的电压-无功潮流模型

为表达方便，本节首先在假设存在网络拓扑及参数的前提下给出电压-无功模型，从而得到电压控制模型。需要强调的是，本文最终采用的迭代控制方法不依赖于本节的潮流模型，且具有更高计算精度。同样地，由于大多数主动配电网拓扑为辐射状，本节以辐射状网络为例给出线性化Distflow 模型下的电压-无功潮流模型，但本文采用的状态空间变换方法并不局限于辐射状网络。

首先，定义主动配电网中各节点所构成的集合为N={0，1，…，N}，节点对(i，j)之间的支路所构成的集合为L={(i，j)}⊂N×N。其中，将配电网参考节点选取为馈线根节点，一般为变电站低压母线。其余变量的定义如图1所示。图中：rij和xij分别为支路(i，j)的电阻与电抗；Vi为节点i的电压幅值；pi和qi分别为节点i的有功功率注入和无功功率注入；Pij和Qij分别为支路(i，j)首端流出的有功功率和无功功率；节点0 代表配电网参考节点。进一步定义Ni⊂N 代表节点i在该主动配电网中的下游相邻节点，即与节点i通过1 条支路直接相连，且相对于参考节点位于下游的节点所构成的集合。

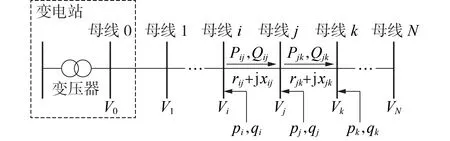
图1 主动配电网符号定义Fig.1 Notation of symbols in an active distribution network

根据线性化Distflow 潮流模型，在忽略有功和无功网损对应的非线性项，并对电压的平方项进行线性替换后，可得到如下支路形式的潮流方程：

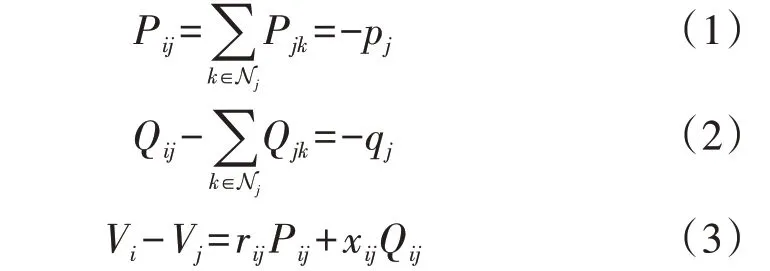
由于线性化过程中的近似假设，上述线性化Distflow 潮流模型的精度有限，在本文中仅用于引出电压优化控制模型。为表述方便，首先需对上述模型采用矩阵化表达。

令主动配电网的原始节支关联矩阵为M0，即该矩阵包含了参考节点对应的行。该矩阵为不满秩矩阵，删去参考节点对应的行后，令剩余的N×N维节支关联矩阵为M。根据定义易知，矩阵M为非奇异矩阵。在此基础上，矩阵形式的支路有功和无功方程可表示为：

式中：P和Q分别为Pij和Qij所构成的列向量；p和q分别为pi和qi所构成的列向量。

式（3）的支路电压方程的矩阵形式为：

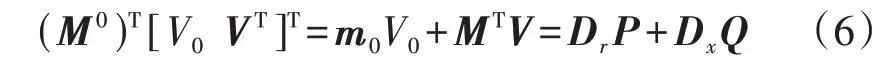
式中：V为Vi所构成的列向量（不包括参考节点）；Dr和Dx为对角矩阵，其对角元素分别为rij和xij。将式（4）、（5）所示的功率方程代入（6）中的电压方程，可得节点电压与注入功率之间的线性方程为：

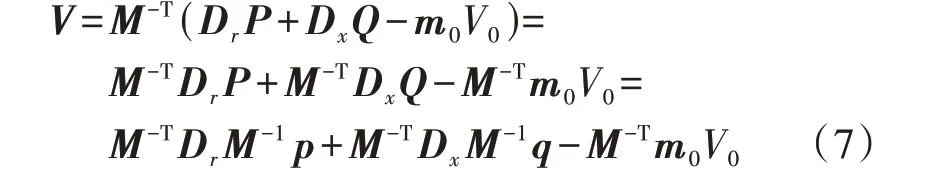
通过令：

式（7）可进一步简化表示为：

1.2 主动配电网电压优化控制模型

在前述线性化电压-无功潮流方程的基础上，以均衡配电网电压分布为目标，构建电压优化控制模型。

1）目标函数。

本文电压优化控制目标为各节点电压与额定值偏差的平方和最小，可通过数学方式表示为：

2）约束条件。

由于潮流约束已在目标函数中体现，本文约束条件主要考虑分布式发电无功调节能力受逆变器容量的约束，对于已知场景，其无功调节量可简化表示为有界约束：

式（13）和式（15）构成了简化的电压优化控制模型，属于有界约束二次规划问题，该问题可以采用集中式优化进行求解。然而，考虑到集中模型的不完备，以及海量分布式发电接入后控制效率与可靠性提升目标，本文提出基于分布式牛顿法的电压优化控制方法，无参数模型下的应对方式将在第3 节中给出。

3）控制对象。

本文无功控制对象仅考虑分布式发电单元（如光伏发电）的无功调节能力及其对电压的影响。事实上，在主动配电网中，更多的电压问题主要依靠无功调压设备解决，如变压器分接头、电容器、静止无功补偿器（static var compensation，SVC）等。上述无功补偿控制设备的共同问题在于其调节通常是离散的档位调节，其动作方式决定了其动作频率受限。但在新能源渗透率较高的配电网中，短时电压波动更为显著，面对这类波动时间短、随机性强的电压波动问题，单纯依靠离散的分接头及电容器档位调整难以满足快速响应控制的要求。因此，无功设备调整可以在离线电压优化问题中通过求解集中优化模型得到解决，由于相关成果较多，本文不再单独考虑。因此本文方法的前提是无功设备已动作完成，在实时在线尺度下完成基于分布式发电单元的无功电压调整，进一步均衡各节点电压分布，可视为动态电压跟踪与控制过程。

2 基于牛顿法的分布式电压迭代控制策略

2.1 牛顿迭代算法

本文采用文献［27］中的分布式牛顿法对电压控制问题进行求解，本节首先介绍算法的控制流程。

为实现分布式迭代，将目标函数分解为各节点本地目标函数fi(Δq(k))之和，fi(Δq(k))如式（16）所示。

式中：Xji为X中第j行第i列的元素；Vj(k)为第k步迭代时节点j的电压幅值；μj为节点j的额定电压。因此，各节点可通过本地及相邻节点电压量测计算本地梯度。将目标函数梯度表示为矩阵形式，如式（18）所示。

式中：ε为迭代步长；d(k)为第k步迭代的牛顿方向；H(k)为第k步迭代的海森矩阵。在实际计算过程中，可通过矩阵C(k)近似替代海森矩阵，按照式（21）进行递推计算。

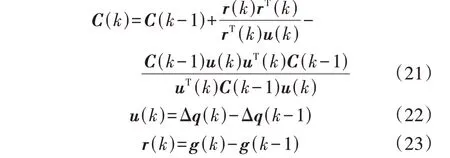
若递推式（21）可分布执行，则牛顿迭代可实现分布式控制过程。

2.2 分布式牛顿迭代控制

因此，节点i的本地牛顿方向可通过将其相邻节点计算的节点i牛顿方向进行求和得到，即：

需要注意的是，由于分布式发电功率因数和容量的限制，各节点无功需满足上下限约束，如式（15）所示。而在牛顿迭代过程中，可能导致无功功率超出范围，因此在实际迭代控制过程中，需要对电源无功进行可行域投影。即一旦节点i的无功功率超出给定的可行域范围，将其功率固定在最接近的可行域边界上，但继续参与分布式迭代，最终得到的迭代结果即为满足约束的全局最优解。由于各节点无功功率上下限彼此独立，因此对原牛顿迭代进行修正可得到各节点的实际迭代结果，利用投影概念表达如下：

综上所述，完整的分布式电压控制迭代过程包括式（17）、（24）—（27）、（30），在此迭代过程中，相邻节点仅需交互Vi(k)、Δqi(k)、(k)等信息，且上述信息都可在各节点本地获取。上述相邻节点信息交互过程如图2所示。

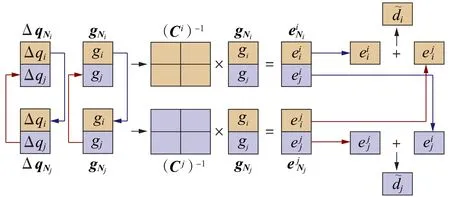
图2 分布式牛顿迭代相邻节点信息交互过程Fig.2 Information interaction process between neighboring buses in distributed Newton iteration

不难发现，上述迭代公式中，式（17）的计算仍需要获取参数Xji以计算本地梯度。事实上，Xji在此处代表节点电压与无功的灵敏度关系，其数值可通过第1 节中的线性支路方程获取，也可通过雅可比矩阵进行计算，但前者由于近似误差，将对电压控制效果产生不良影响，而后者则仅可在运行点附近取得较好的结果。且无论哪种方法，均依赖精确的参数模型，一旦参数精度不足，电压控制效果及收敛性均无法保证。针对该问题，本文将在第3 节中提出数据驱动的全局高维线性潮流等值方法，从而计算精确牛顿迭代方向。

3 基于状态空间线性变换的牛顿方向计算

3.1 基于Koopman的状态空间升维线性变换

基于状态空间线性变换的分布式电压控制可以划分为2个层级。

1）模型训练层。通过离线方式，以输出变量样本（节点电压与相角历史量测数据）和输入变量样本（节点注入无功功率和有功功率历史量测数据）作为训练样本输入，构建升维线性潮流模型，训练得到线性潮流矩阵L，将对应的潮流矩阵元素以广播通信的方式下发至各节点。上述训练的结果在网络结构不发生变化的情况下，无需频繁更新，因此可由以日到月为周期离线训练与更新。

2）分布式控制层。利用数据驱动求得的Xji结果，根据实时电压量测更新灵敏度Xji的值，并基于实时电压量测计算本地梯度，通过相邻节点交互通信的方式计算牛顿迭代方向，实现分布式牛顿法的在线电压控制，优化配网中的电压分布。

在网络拓扑不变的情况下，模型训练层下发的结果始终适用，仅需周期执行校正其数值即可，因此在在线的电压控制过程中并不体现。当主动配电网发生重构后，模型训练层基于运行数据重新更新和训练潮流矩阵，结束后下发至各节点，各节点继续执行在线分布式电压控制即可。相反地，分布式电压控制层以在线方式执行控制，以应对电压波动。因此，单纯以电压控制流程而言，本文方法仍属于分布式电压控制，但加入了“集中训练-分布控制”的分层模式，与电网云边协同调控思路相符，以求在不具备完备模型参数的情况下得到更精确的牛顿迭代方向。2 层控制架构的层级关系及数据交互框架如图3 所示，其中DRG 表示分布式可再生能源发电，[·]M代表矩阵的Moore-Penrose逆。

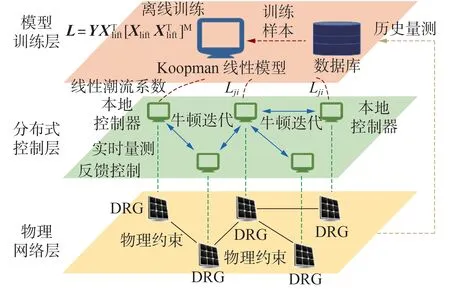
图3 双层电压控制架构Fig.3 Framework of double-layer voltage control

本质上，配电网精确潮流应为非线性方程，而根据Koopman 理论，非线性方程可在无穷维Hilbert 空间中映射为线性方程且不失精确性。本文即利用上述理论，通过历史运行数据样本，训练得到升维空间中的线性潮流方程。事实上，实际训练过程中，仅需将状态空间升维至几千维，其模型精度即可满足要求。上述状态空间变换示意图如图4所示。

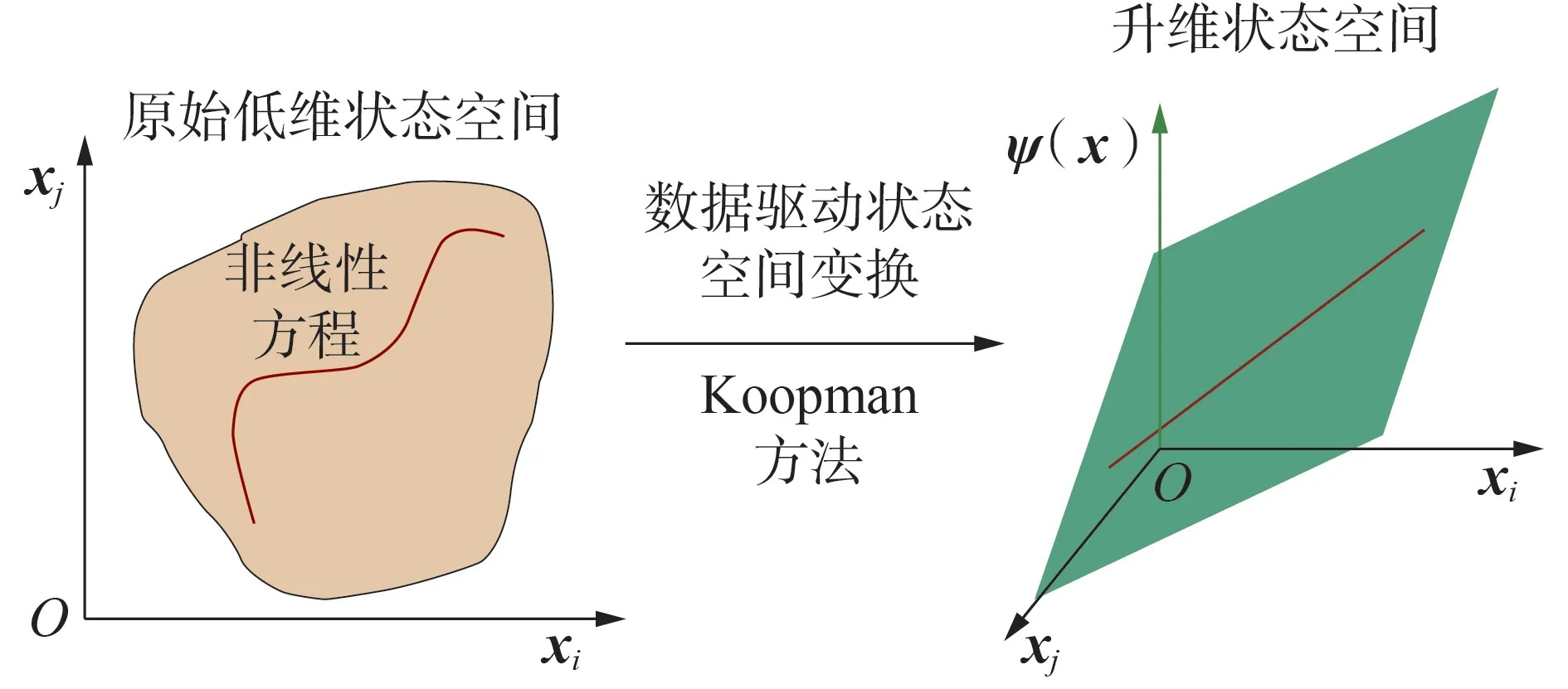
图4 状态空间升维变换示意Fig.4 Schematic diagram of state space lift-dimension transformation

具体而言，假设配电网中的非线性潮流方程可表示为如下方程：

式中：y为状态变量，其包括节点相角及电压幅值，y=[VTθT]T；x为K维输入变量，其包括节点注入有功和无功功率，x=[pTqT]T。

状态空间变换需对输入变量进行升维，令xlift表示升维后的输入变量，ψ(x)表示升维扩充出的m维输入变量，则升维后的线性潮流方程可通过线性矩阵L表示为：

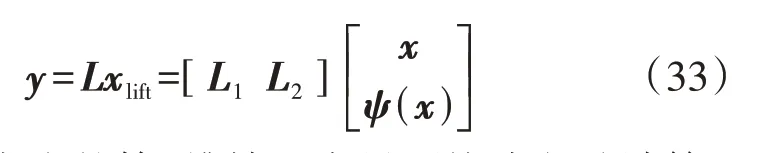
升维扩充出的第i维输入变量可按式（34）计算。

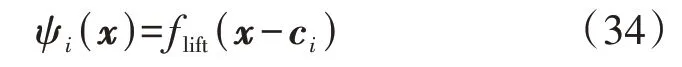
式中：ci为随机生成的K维基底向量；flift为升维函数。一般而言，升维函数的选取可采用典型方式，如基于基本函数的polyharmonic、invquad、invmultquad等方法。本文采用polyharmonic升维函数，其具体形式可表示为：

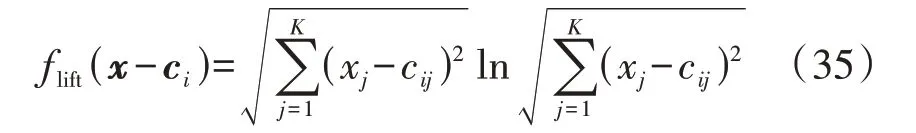
式中：xj为x中的第j个元素；cij为ci中的第j个元素。

为获得线性矩阵L的结果，可利用历史运行数据构造训练样本集，以X代表输入变量样本矩阵，以Y代表状态变量样本矩阵。各样本集包括S个时间断面的输入变量和状态变量值。利用式（35），可计算升维后的输入变量样本矩阵Xlift。在相同时刻得到的量测输出变量与升维后的输入变量共同构成一组训练样本。在此基础上，利用最小二乘方法估计线性矩阵L的值，如式（36）所示。

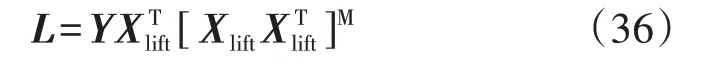
基于线性矩阵L的值，可得到配电网高维全局线性潮流关系，L为常矩阵，即在网络拓扑保持不变的前提下，任何工况下均能够体现节点电压、相角与注入的无功、有功之间的关系，且不依赖于模型参数，线性化效果亦不局限于平衡点附近，而是全局线性化的矩阵。在此基础上，可进一步推导计算Xji的值。状态空间线性变换方法能够基于有限的运行数据构建符合全局的高维线性潮流关系，并不需要训练样本覆盖所有工况，这是因为Koopman 方法构造出反映配电网本身物理特征的高维线性等效潮流模型，该模型可适用于所有拓扑结构不改变情况下的运行工况，而无需在训练过程中即覆盖全部越限场景。在训练过程中，电压越限样本可用于模型训练，但并非必需，这降低了训练数据获取难度；而对于导致配电网结构变化的断线、短路等故障，由于改变了配电网潮流模型，因此需要排除出训练集。若配电网结构因重构而发生变化，则应根据当前的结构进行重新训练。

3.2 基于升维线性潮流的牛顿方向计算

根据线性矩阵L的定义，节点j电压幅值与节点i无功调节量之间的灵敏度可按式（37）进行计算。

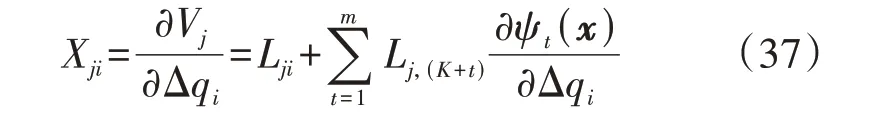
式中：Lji为矩阵L中对应电压Vj和无功调整量Δqi的元素；Lj，(K+t)为矩阵L中对应电压Vj和升维扩充出的第t维输入变量ψt(x)的值。

式（37）中的偏微分项可按式（38）进行计算。

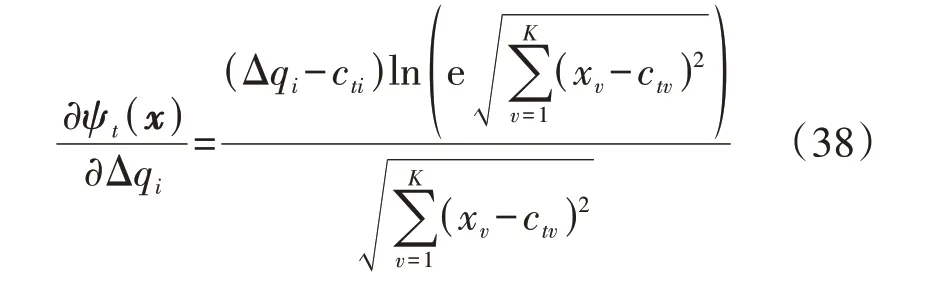
因此，在数据驱动得到的升维线性潮流矩阵的基础上，根据式（17）、（37）、（38），即可计算本地梯度的精确值。模型训练层下发的结果相当于生成了灵敏度的全局计算公式，因此各节点仅需根据当前运行状态即可对灵敏度进行更新，因此该灵敏度计算方法是“全局”的，并以此根据第2 节中的方法更新牛顿迭代方向。在此过程中，梯度的计算完全不依赖于任何模型参数，因此在模型参数不精确或不完备场景下，分布式电压控制效果及收敛速度不受影响。

在网络拓扑不变的情况下，模型训练层下发的结果始终适用，仅需周期性地校正其数值即可，因此在在线的电压控制过程中并不体现。相反地，分布式电压控制层以在线方式执行控制，以应对电压波动。应用模型训练结果进行分布式电压控制的整体流程如图5所示。

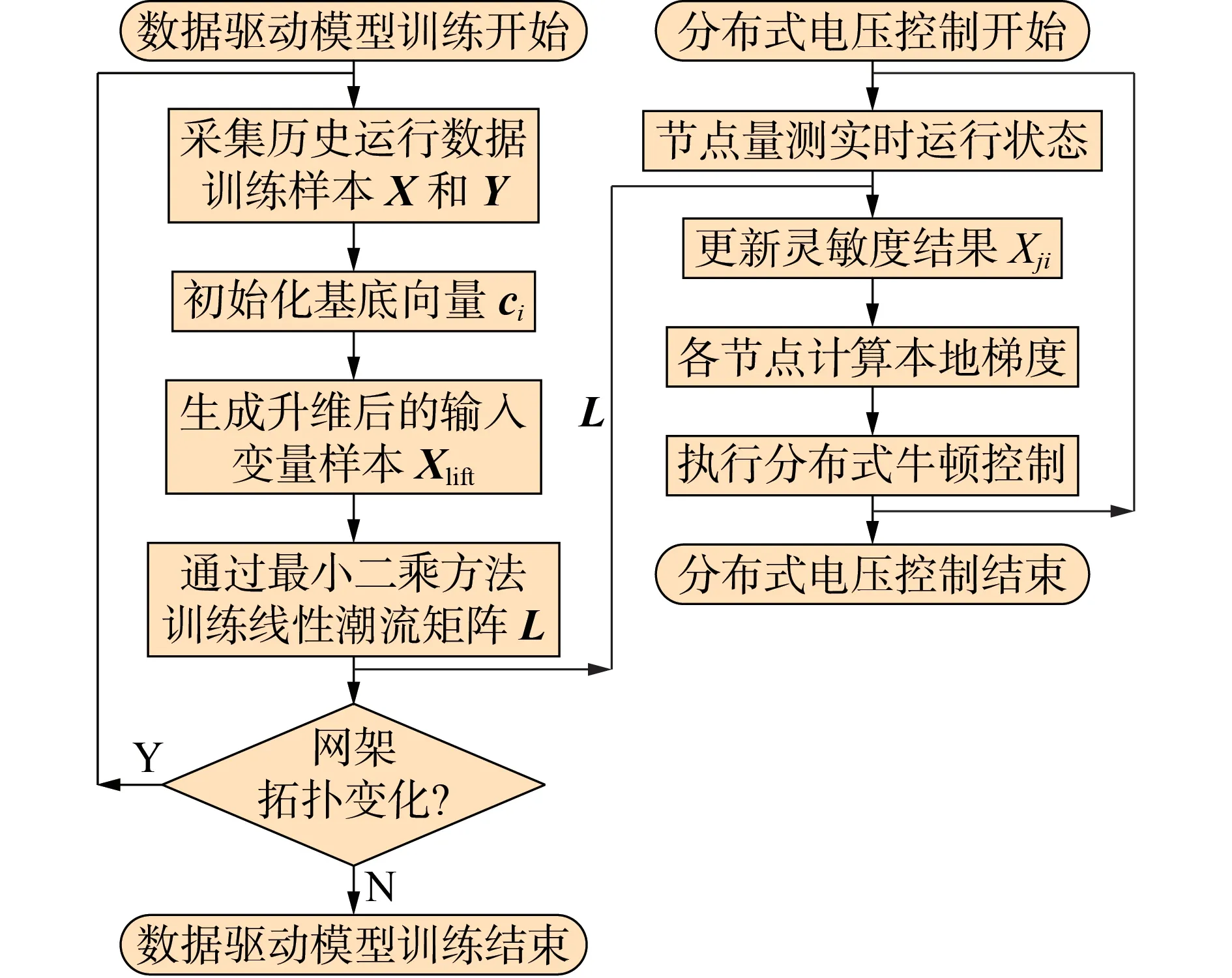
图5 分布式电压控制整体流程Fig.5 Overall process of distributed voltage control

4 算例分析

本节利用MATLAB 软件在IEEE 33、69和118节点标准算例系统中对本文所提出的分布式电压控制方法进行效果验证。为模拟主动配电网中接入分布式发电的情况，在各算例系统中，分别添加3 种不同比例15%、30%、50%（按照光伏容量与负荷比值计算）的分布式光伏。在电压控制过程中，变电站低压母线和参考节点电压始终假设为1 p.u.，且各节点安全电压约束为［0.95，1.05］p.u.。

4.1 IEEE 33节点算例系统分析

为确定合适的升维维数与样本集数量，在IEEE 33 节点算例系统下，利用MATPOWER 潮流计算得到样本数据，利用数据驱动训练得到的线性潮流计算1000组测试场景下的节点电压分布，并将其与精确参数下的牛顿-拉夫逊潮流进行对比，以此评估数据驱动模型训练精度。变换不同升维维度与样本数量，得到的对比结果如表1 所示。表中，最大误差和平均误差均为标幺值。

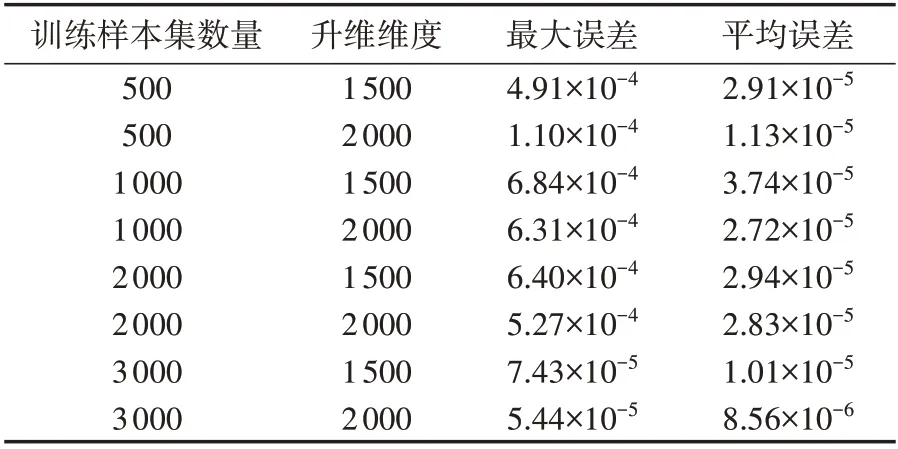
表1 数据驱动模型训练精度Table 1 Accuracy of data-driven power flow model

不难发现，数据驱动线性潮流模型下电压计算结果与精确结果间的偏差均在10-3p.u.数量级以下，精度很高，且误差总体趋势随着样本数量及升维维度的增加而减小。考虑计算时间与数据的获取难度，本文算例最终选择的样本数量为3 000 个，升维维度为2000。

利用MATPOWER 计算分布式光伏无功调整后的潮流分布，此处采用精准模型参数，以该结果作为配电网电压实际状态反馈。本文在每个算例系统中的每种光伏装机与负荷比值下，均采用MATPOWER计算3000个断面潮流结果作为样本集，并通过状态空间变换将潮流模型升维至2 000 维，从而计算电压-无功灵敏度结果。

为验证本文方法的效果，将其与利用第1 节的线性化Distflow 模型的分布式电压控制结果进行对比，并同时分析模型参数精确与不精确2 种情况，以此验证本文在模型参数不精确情况下的优势。其中不精确的模型参数通过在各支路电抗值上额外添加±a（a∈[3%，8%]）的扰动进行模拟。同时，以基于MATPOWER 的集中式最优潮流结果作为理论最优解，对比不同方法的效果差异。事实上，为证明本文方法的效果，还应与神经网络等数据驱动方法进行对比，但目前已有文献中神经网络方法很难与分布式控制实现有效结合，相关讨论计划在后续文章中进行。不过，可以确定的是，相比“纯数据驱动”的神经网络方法，本文基于Koopman 算子状态空间映射的方法本质上在另一空间中构造出了等效的线性机理模型，更适合全局应用的需求，这一优势是神经网络方法所不具备的。

在算例讨论中，分布式电压控制的精度与效果主要由最终控制达到收敛时的电压分布和迭代达到收敛的速度决定。事实上，牛顿迭代过程中每一步的方向都将影响最终达到的控制效果及收敛速度。因此，下文的讨论主要围绕这两方面进行。

首先，以IEEE 33 节点测试系统中添加15%分布式光伏为例对比不同方法收敛性与控制效果。需要强调的是，在实际场景分布式控制过程中，光伏与负荷功率始终处于变化过程中，不存在收敛的情况，因此分布式控制本质上在于始终跟踪电压的动态波动，向电压优化分布的方向进行迭代控制，改善电压分布。为更好地进行对比分析，算例控制过程中假设功率不发生波动，以直观对比各方法的收敛速度。由于牛顿迭代中，两步间隔时间可人工设定，一般可选为秒级甚至百毫秒级，一旦迭代步之间的时间间隔确定，收敛所需时间即完全取决于收敛所需迭代步数，为使对比更具一般性，本文算例中采用迭代收敛步数作为方法间控制效率的对比指标。图6 给出了3 种不同方法下目标函数值随着迭代控制次数的变化曲线。可以看出，在本文方法的控制下，目标函数值在8 次迭代左右达到收敛，其速度明显快于另外2 种情况，这是由于采用了数据驱动的潮流结果计算全局灵敏度，从而对牛顿迭代方向进行更新。相比采用Distflow 模型的方式，本文方法未进行忽略和近似，因此收敛更快。而基于Distflow 模型的方法，在模型参数精确的前提下需要11 步迭代控制收敛，且最优性方面与本文方法也存在一定差距。若在模型参数不精确的场景下，其收敛不仅需要22 步迭代控制，且最优性也无法保证，目标函数值与理论最优结果差距很大。由此可见，基于模型的分布式控制方法对模型参数精度依赖性较高，而本文则能解决这一问题。在实际工程运行中，配电网模型参数存在偏差是较为常见的情况，甚至中低压配电网可能出现完全无模型的情况。因此，本文所提出的方法具有更好的工程适应性。

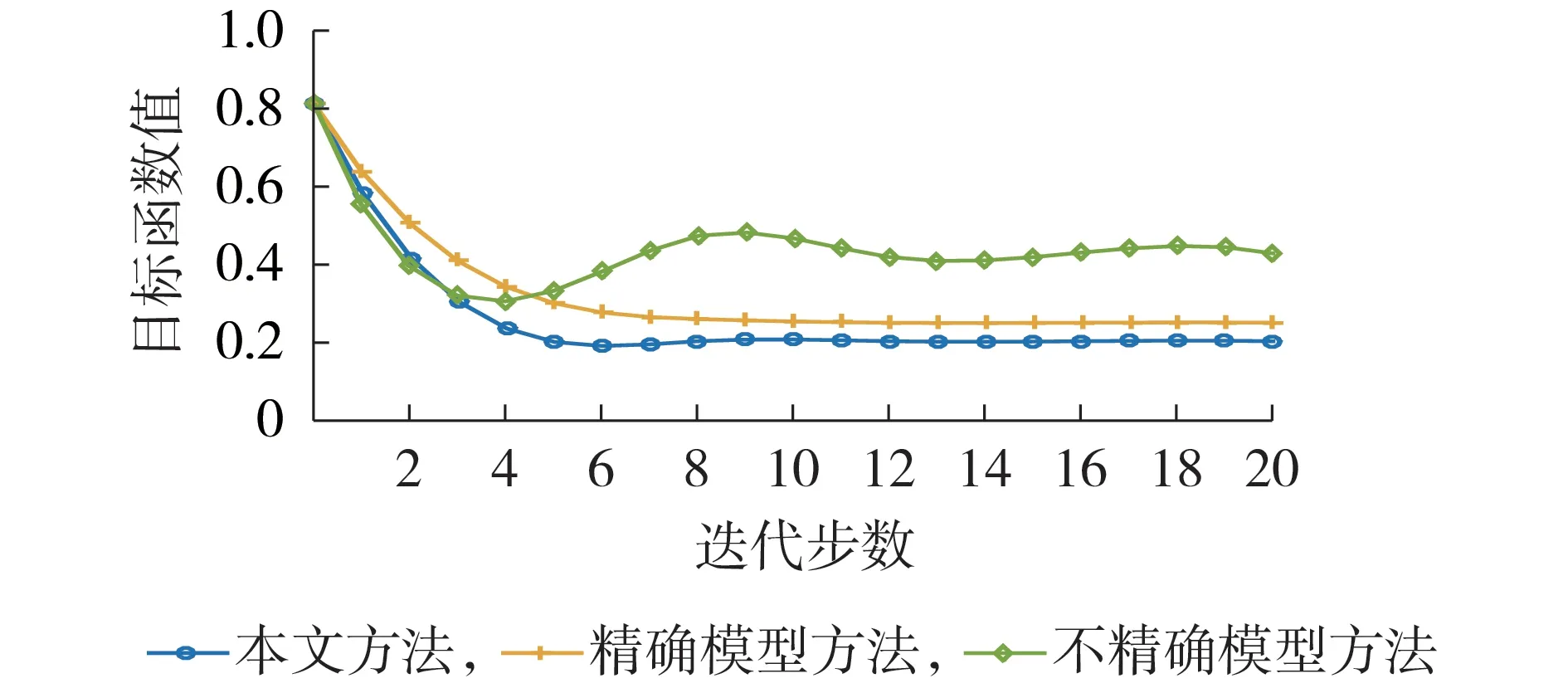
图6 IEEE 33节点系统中目标函数随迭代过程的变化Fig.6 Objective value variation with iteration in IEEE 33-bus system

在同样的算例条件下，最终达到收敛时不同方法下的电压分布如图7 所示。为方便对比，无控制下的自然电压分布同样在图7 中给出。图中，电压幅值为标幺值。可以看到，在本文所提控制方法下，配电网中的电压分布更加均衡，且解决了自然电压分布下的越限问题。与之相比，基于Distflow 模型的分布式控制结果无法完全消除电压越限，且随着参数误差的增加，电压越限问题更为突出，从而验证了所提控制方法的电压控制效果。这是由于Distflow模型获取灵敏度的推导过程中，忽略了有功和无功网损对应的非线性项，并对电压的平方项进行了线性替换，因此迭代效果不及本文基于数据驱动校正后的分布牛顿法。一旦参数不精确，基于模型的方法收敛速度、目标函数最优性、电压分布效果将出现更显著的下降，而本文方法则不受参数精度影响。

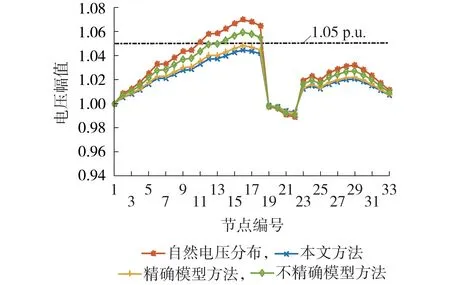
图7 IEEE 33节点系统中的电压分布Fig.7 Voltage distribution in IEEE 33-bus system

在本文方法控制收敛后，相较自然电压分布下的无功功率，IEEE 33节点系统开环下各节点无功调节量如图8 所示。图中，节点无功调节量为标幺值（功率基值为10 MV·A）。可以看出，各节点无功调整具有响应本地电压变化的特点，同时兼顾全局电压的分布，最终实现电压的优化控制。

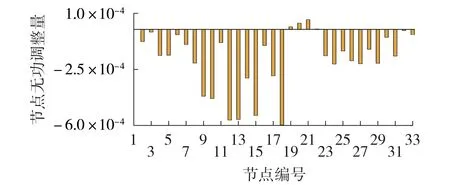
图8 IEEE 33节点系统中各节点无功调整量Fig.8 Reactive power adjustment of each node in IEEE 33-bus system

4.2 IEEE 69、IEEE 118节点算例系统分析

为进一步验证其他算例场景下的效果，本文对比了IEEE 69 节点算例系统添加15%分布式光伏后的分布式电压控制收敛过程，具体结果见附录A 图A1—A4、表A1。该场景下，本文方法需要23 步达到收敛，而基于模型的方法分别需要26步和58步达到收敛，且收敛结果均不如本文方法。在IEEE 118节点算例系统中添加15%分布式光伏后，本文方法需要28步达到收敛，而基于模型的方法分别需要78步和152 步达到收敛。可以看出，随着节点数量的增加，本文方法收敛速度下降并不显著，而基于模型的方法由于误差的累积，收敛速度则显著下降。

为进行更加全面的分析，3 种方法下在各种算例系统中的不同光伏装机容量与负荷功率的比值场景下的收敛所需次数均进行了对比。在所有算例系统的所有光伏装机容量与负荷功率的比值下，本文所提出的方法都以最快的速率收敛到最优值，其收敛性优势随着系统规模的增加体现得愈发明显，验证了本文方法的效果。

4.3 环网下适用性分析

为验证本文方法在环网下的适用性，采用IEEE 33节点标准算例系统，将系统中5个联络开关闭合，产生5 个环路，各节点光伏配置情况与原33 节点算例相同，分布式光伏占比为15%，同样将本文方法所得结果与利用第1 节的线性化Distflow 模型的分布式电压控制结果进行对比，并同时分析模型参数精确与不精确2 种情况，以此验证本文在模型参数不精确情况下的优势，其中不精确的模型参数仍在各支路电抗值上额外添加±a（a∈[3%，8%]）的扰动，对应的结果见附录B图B1、B2。

在本文方法的控制下，目标函数值仍在7 次迭代左右达到收敛，相比基于模型的方法在模型参数精确的前提下12 步收敛，模型参数不精确的场景下24 步收敛，本文方法收敛速度更快，且目标函数优化结果也强于另外2 种方法，这是由于在迭代方向计算过程中未进行近似。

此外，在本文控制方法下，环网中的电压分布更加均衡，电压控制效果相较另外2 种方法更优，由此验证了本文提出的方法在环网条件下同样适用。

5 结语

本文提出了一种基于状态空间线性升维变换的主动配电网分布式电压控制方法。通过利用矩阵分裂方法，实现了海森矩阵的分布式求逆，从而将分布式控制敛速提升至超线性收敛，更适合在线应用。随后，本文基于Koopman数据驱动方法，利用配电网历史运行数据作为训练样本，构建高维线性精确潮流模型，从而推导得到电压-无功全局灵敏度，以此校正分布式牛顿控制中的迭代方向。算例分析采用改造后的IEEE33、69、118节点系统进行了方法效果和收敛性的验证。相比依赖于模型的分布式电压控制方法，本文方法具有更快的收敛速度和更优的控制收敛结果，且不受参数不精确问题影响，具有更强的工程适用性。

附录见本刊网络版（http：//www.epae.cn）。