基于Stackelberg博弈的配电网分布式光伏低碳化消纳方法

张 涛，杨建华，靳开元，李嘉彬，杨志杰

（1. 中国农业大学信息与电气工程学院，北京 100083；2. 国网天津市电力公司，天津 300010；3. 国网冀北电力有限公司经济技术研究院，北京 100038；4. 普洱市公安局，云南普洱 665000）

0 引言

在“双碳”战略目标下，新能源发电以及低碳化消纳方法将成为一个重要研究方向。然而，受电网自我调节能力和不完善市场机制的限制，大规模光伏（photovoltaic，PV）发电消纳问题日益突出。为应对节能减排和大规模光伏发电消纳困境，许多学者进行了相关研究。文献［1］采用发电量收入、光伏成本、损失效率改善和储备容量成本4 个指标，分析光伏发电的碳排放特征和经济效益。文献［2］分析需求侧资源参与电网调度的可行性，考虑多种低碳化途径，建立基于柔性负荷分类的综合低碳效益模型。文献［3］量化评估电力系统关键技术进步与低碳转型经济可行性的耦合与匹配关系，提出了二者协同优化的框架和方法。文献［4］研究碳交易机制的引入对电力系统优化运行的影响，基于电网基准线排放因子，对初始碳排放额度进行分配，提出低碳经济下含光伏发电的优化调度模型。文献［5］将低碳手段与市场机制相结合，搭建考虑碳交易的光热电站与风电系统运行框架，并分析其运行机理。文献［6］为实现系统低碳经济调度，综合考虑低碳性和经济性，提出包含阶梯式碳交易的电-气-热综合能源系统低碳经济调度模型。文献［7］通过模糊层次分析法对发展态势与市场状态2 个指标进行赋权，对“双碳”目标下共享储能模式应用于新能源消纳进行评价。

为使得售电公司购售电收益和居民用户综合效用最大，可以建立售电公司与居民用户的非完全信息Stackelberg 博弈模型［8］。文献［9］为最大化微电网收益，建立基于Stackelberg 博弈的双层优化调度模型，得到最优内部电价和充换储一体化电站的最优充、放电计划。采用逆向归纳法获取博弈模型的纳什均衡解，并对比分析不同电价策略下的最优电价与最优用电量，能够确定基于分时电价的最优制定策略［10］。分时电价对提高电力系统的整体经济效益具有一定作用［11］。通过制定分时电价，可以进一步提高农业园区用户利用时移负荷进行大规模分布式光伏就地消纳的意愿，构建园区分时电价优化模型［12］。已有学者从宏观方面对光伏的低碳化概念以及评估理论进行了研究，但是，对于低碳化背景下的分布式光伏发电，还缺乏交易电价与可时移低碳化负荷协调消纳的相关研究。

因此，本文针对配电网分布式光伏发电功率不能大量就地消纳的问题，以最优交易电价为变量构建配电网的农业园区方综合收益函数，研究分布式光伏就地消纳的低碳运行效益；以光伏发电和农业园区方整体综合收益最大为目标函数，通过Stackelberg 博弈模型确定最优交易电价和各农业园区的最优时移消纳功率；在满足就地消纳违约率约束要求的情况下，确定不同农业园区的最大低碳消纳效益。

1 光伏就地消纳收益模型

1.1 农业园区收益模型

1.1.1 可时移负荷消纳光伏电量收益

根据农业生产用电特性，综合西部多省峰谷电价的划分，给出农业园区峰谷电价如附录A 表A1所示。

1.1.2 低碳化农业用电收益

光伏发电功率不能大量就地消纳的时段通常是农业用电的平时段，以平时段电价参与用电设备的低碳效益计算。农业园区用电设备的低碳效益包括两部分：一部分是通过提高生产效率来减少电能和农药化肥用量的低碳效益；另一部分是处理动物粪便避免的碳排放和加工售卖收益。参考国内碳交易价格，本文取CO2的碳交易价格为0.052 8 元／kg。已知生产1 kW·h 的煤电，需要排放CO2约0.997 kg，排放粉尘0.272 kg，排放SO2约0.03 kg，排放NOx约0.015 kg。而煤电生产时CO2、粉尘、SO2、NOx的环境价值分别0.023、2.2、6、8元／（kW·h）［15］，则传统煤电生产单位电能的环境价值为0.9739元／（kW·h）。

以种马铃薯为例，在温室中其生长周期一般为2.5 个月。通常化肥使用量约为0.032 85 kg／m2［16］，杀虫农药使用量约为0.007 5 kg／m2。化肥市场价约为20 元／kg，并且使用1 kg 化肥的CO2排放量为0.8956 kg；农药市场价约为0.3750元／m2，并且使用1 kg农药的CO2排放量为4.9341 kg［17］。

种植温室部分设备配置情况为：空气源热泵2 台，额定功率为8 kW；蓄水泵1 台，额定功率为2.2 kW；水肥一体化机1 台，额定功率为1.5 kW；远红外加热装置1 台，额定功率为3 kW；等离子固氮机1台，额定功率为0.3 kW；物理杀虫器2台，额定功率为0.35 kW；声波助长设备2 台，额定功率为0.35 kW。

取空气源热泵冬季的能效比为3［18］，认为电加热能效比为1，则相比于电加热方式，其低碳效益为2.865 元／（kW·h）；蓄水泵与水肥一体化结合使用可降低灌溉用水量50%［19］，提高化肥利用率21.67%［20］，则两者低碳效益均为0.825元／（kW·h）；远红外加热相比于电加热节能50%［21］，则其低碳效益为0.711 元／（kW·h）；物理杀虫器可节省农药40%［22］，则低碳效益为0.478 元／（kW·h）；声波助长设备可使农作物增产10%［23］，减少病虫害8.4%［24］，则其低碳效益为0.446元／（kW·h）。

在养殖过程中，每头牛每天产生约21.09 kg 粪便［25］，CO2含量约67.2 g。牛粪烘干处理后含水量约50%，售价约250 元／t。有机肥加工的原料为干牛粪，加工设备的处理能力取决于牛粪烘干机，有机肥售价约600元／t，忽略加工中的损耗，则所有加工设备的低碳效益为350元／t。

养殖温室按照养牛数量配置用电设备。通常，每300 头牛配置10 台牛粪清理机和1 台牛粪烘干机，单台额定功率分别为2.2 kW 和7.5 kW，清理与烘干处理能力为2 t／h；有机肥加工设备包括翻堆、粉碎、搅拌、造粒、包装机，额定功率分别为18、22、7.5、22、3 kW，加工处理能力为1 t／h；空气源热泵2 台，额定功率为8 kW；蓄水泵2 台，额定功率为2.2 kW。其中，养殖园区一般只配备一套有机肥加工设备，与养牛数量无明显增长关系。

本文不考虑粪污处理过程对牛类生长的影响，牛粪清理机与烘干机配套使用生产可以进行售卖的干牛粪，构成其低碳效益，两者的低碳效益均为8.486 元／（kW·h）；所有加工设备的加工能力取值为1 t／h，则低碳效益为4.827元／（kW·h）。

1.2 光伏发电方收益模型

1.2.1 就地消纳的低碳效益

若仅考虑光伏发电相对煤电在同等电量下节省的污染物环境价值，假设共有n个农业园区，则光伏发电方在T内的低碳效益如式（3）所示。

式中：e1为传统煤电生产单位电能的环境价值，由上述讨论可知，e1取值为0.9739元／（kW·h）。

1.2.2 光伏发电碳成本

光伏板的生产需要使用传统煤电，运输安装时也会产生CO2，假设此部分碳排放通过参与碳交易成为光伏发电的固定碳成本。光伏电站运行维护阶段的碳成本主要是破损光伏板的替换和光伏设备维护的碳排放，研究表明光伏电站运维可变成本为0.004 2 元／（kW·h）［26］，将其作为光伏发电的运维可变碳成本。生产和运输1 MW 光伏系统所产生CO2约为1 924.378 t［27］，因此，光伏发电碳成本折算到T内为，如式（4）所示。

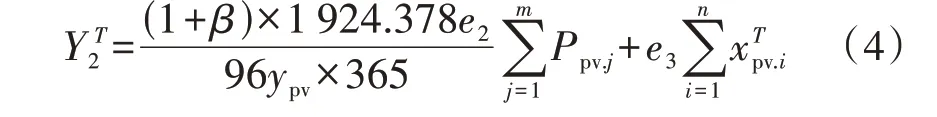
式中：β为运维过程与生产运输过程碳排放的比例，取5%［27］；ypv为光伏有效使用年限，一般为25 a；Ppv.j为第j个光伏电站的接入容量；e2为CO2的碳交易价格，根据上海环境能源交易所公布的数据，其值为0.052 8 元／kg；e3为光伏发电的运行可变碳成本，取0.0042元／（kW·h）；m为光伏电站的数量。

光伏发电方在T内的低碳运行效益如式（5）所示。

1.2.3 光伏发电方售电收益

式中：pgs为集中式光伏电站指导电价；ppol为补贴电价；pμ为过网费。

国家能源局出台的《关于开展分布式发电市场化交易试点的通知》指出，过网费可以取为10 kV 与35 kV 输配电价之差，以甘肃省输配电价为例，此时pμ=0.2965-0.2865=0.010元／（kW·h）。

2 最优交易电价和低碳消纳控制双层优化模型

2.1 最优交易电价就地消纳模型

采用Stackelberg 博弈模型证明存在纳什均衡，以光伏发电方为领导者、农业园区方为跟随者，通过最大化两者整体综合收益，确定最优交易电价［28-29］。为节省农业园区的用电成本，需要满足ps≤p′g。

在TPV内，以最大化光伏发电方和农业园区方整体综合收益F1为目标函数，如式（8）所示。

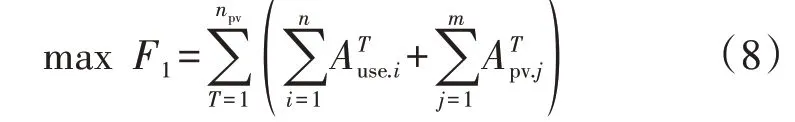
并非所有的博弈都存在数值解，但可以证明该博弈模型存在最优解，即存在最优交易电价，其证明的过程如附录B所示。

证明最优交易电价ps.best存在后，确定光伏发电方最优博弈策略为Ω T(ps.best)。光伏发电方收集博弈信息后，根据式（9）判断最优时移消纳光伏电量是否满足农业园区当前时段最大负荷限制，根据式（10）判断其是否满足当前时段光伏最大待消纳电量限制，若越限则取临界值。

按照电压质量的相关标准，光伏并网母线电压偏移不得超过额定电压UN的±7%，如式（11）所示。

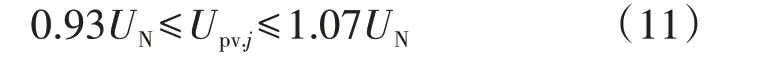
式中：Upv.j为第j个分布式光伏电站的并网母线电压。

2.2 农业负荷低碳消纳控制模型

通过控制农业负荷可以确保农业园区获得最大低碳消纳效益。以农业园区i在T内的最大低碳消纳效益为目标函数，如式（12）所示。

3 仿真分析

3.1 双层控制仿真流程

上层为最优交易电价就地消纳模型，控制模型以maxF1为目标函数，考虑光伏并网母线电压限制条件，采用Stackelberg 博弈求解ps.bset以及各农业园区。求解流程图见附录C图C1。

由上图可以发现未完成的任务主要集中在广州市以及深圳市，而东莞市的任务则大多都被很好地完成了。我们通过查阅三处城市的社会经济特征，发现东莞市的经济发展状况比广州市和深圳市的差，并且人口以年轻人以及女性偏多。年轻人接受新鲜事物快，并且一些在校学生以及全职太太更倾向于通过完成任务的方式获得一些报酬，所以任务完成率更高。

下层为农业负荷低碳消纳控制模型，优化模型以maxFTarg.i为目标函数，采用改进的非支配排序遗传算法（non-dominated sorted genetic algorithm-Ⅱ，NSGA-Ⅱ）以实数形式编码和，求解Pareto 最优解。求解流程图见附录C图C2。

3.2 最优交易电价仿真

以IEEE 33 节点配电网为例进行仿真分析，如图1 所示，该配电区域总负荷为3.78+j1.135 MV·A，线电压的基准值为12.66 kV。

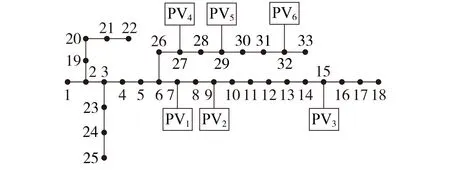
图1 IEEE 33节点配电网结构Fig.1 Structure of IEEE 33-bus distribution network

假设有6 个集中式并网的村级光伏电站，安装在节点7、9、15、27、29、32，接入容量分别为1100、1 100、600、1 000、900、600 kW。假定有32 个农业用户，其中节点11 和节点12 分别为种植园区1 和园区2，节点29 和节点30 分别为养殖园区1 和园区2，其余节点为普通农业居民用户，负荷信息见附录C表C1。

为保证农作物在冬季能够正常生长，温室需要使用电加热设备。本文以冬季典型日为例，给出养殖园区、种植园区、普通农业居民负荷曲线和不考虑电压越限时的光伏出力曲线如图2 所示，图中功率为标幺值。由于分布式光伏安装处相距不远，所以认为所有光伏的发电特性相似。

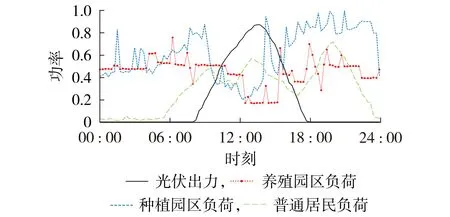
图2 不同类型负荷以及光伏出力的曲线Fig.2 Curves of different types of loads and PV output

假定IEEE 33 节点配电网位于第Ⅱ类资源区，根据国家发展改革委出台的《关于2020 年光伏发电上网电价政策有关事项的通知》可知，集中式光伏电站指导电价pgs为0.40 元／（kW·h），补贴电价ppol调整为0，则光伏上网电价pA为0.39元／（kW·h）。

通过仿真计算，确定最优交易电价和农业园区最优时移消纳光伏功率；对比在采用所提分布式光伏就地消纳方法前后，光伏发电方和农业园区方整体综合收益、光伏电站弃光电量、低碳运行效益等方面的变化。

在引入最优交易电价就地消纳模型前，光伏出力时段08:00—18:00内各光伏并网母线电压波动如图3所示，图中电压为标幺值，后同。

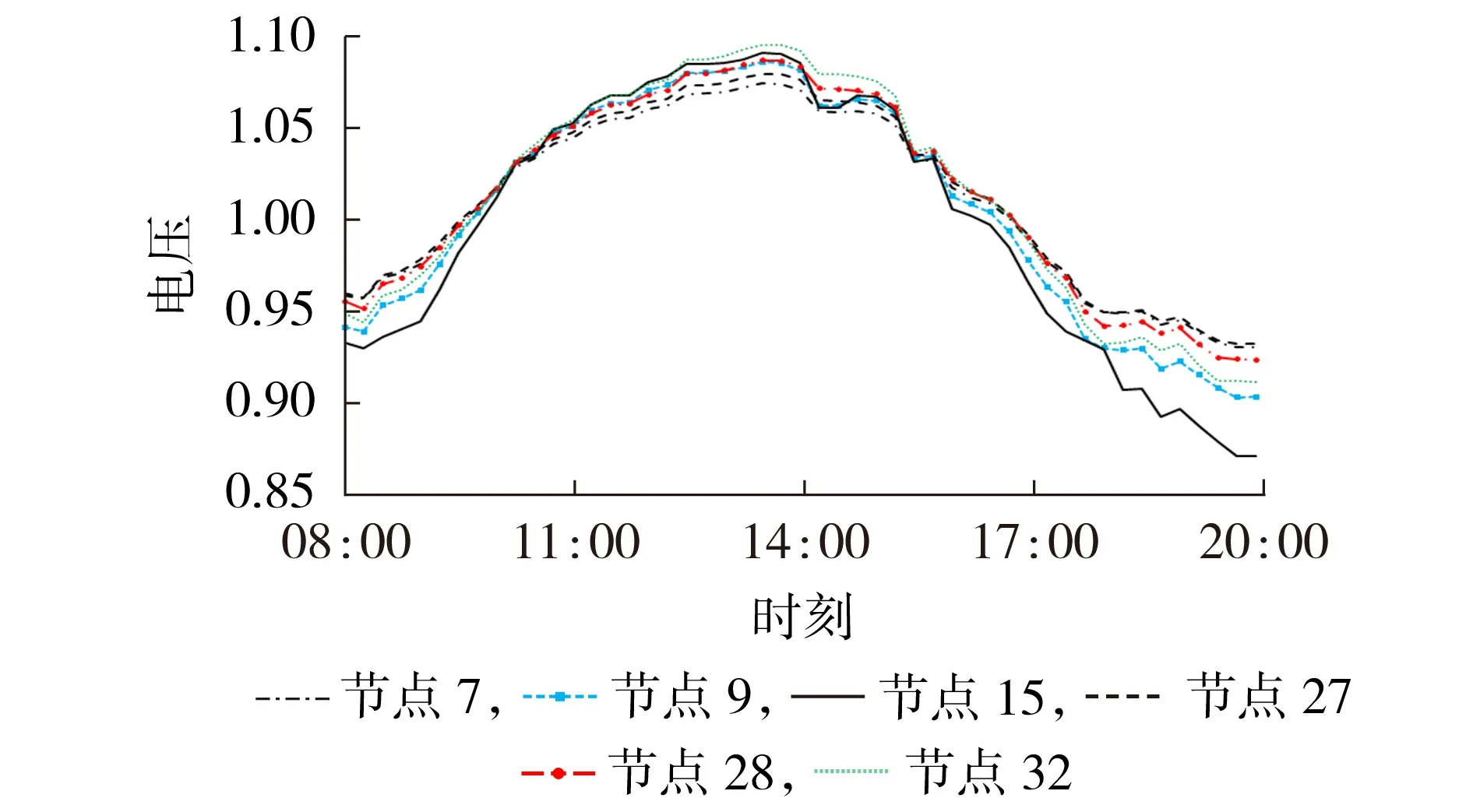
图3 光伏并网母线电压波动Fig.3 Grid-connected bus voltage fluctuation of PV

由图3 可知，光伏并网母线电压在时段12:00—14:45 之间出现越限，电压偏移超过规定值7%。为保证电压质量，分布式光伏电站不得不限制出力。为确保所有时段内各光伏并网母线电压波动均在正常范围内，分布式光伏电站PV1—PV6在时段12:00—14:45 之间的弃光电量分别为730.664、487.109、243.554、487.109、243.554、487.109 kW·h，弃光现象比较严重。取TPV为12:00—14:45，在该时段内对分布式光伏电站待消纳电量进行就地待消纳控制。

设置ps的仿真步长为0.001元／（kW·h），光伏发电方选择交易电价ps从0.350 元／（kW·h）变化到0.450 元／（kW·h）时，在整个TPV内，F1与ps的关系如图4所示。

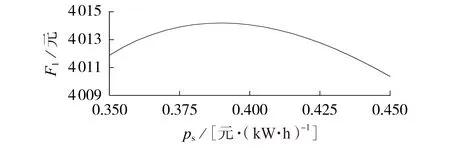
图4 F1与ps的关系曲线Fig.4 Curve of relationship between F1 and ps

由图4 可知，当光伏发电方选择最优交易电价ps.best=0.390 元／（kW·h）时，F1取得最大值，为4 014.222 元，即光伏发电方最优博弈策略为Ω T(0.390)。由于所选计量时段为15 min，且认为此时段内用电设备功率和光伏出力不变，则有=0.25P，根据博弈关系式（14），确定各农业园区满足约束的最优时移消纳功率P如表1所示。

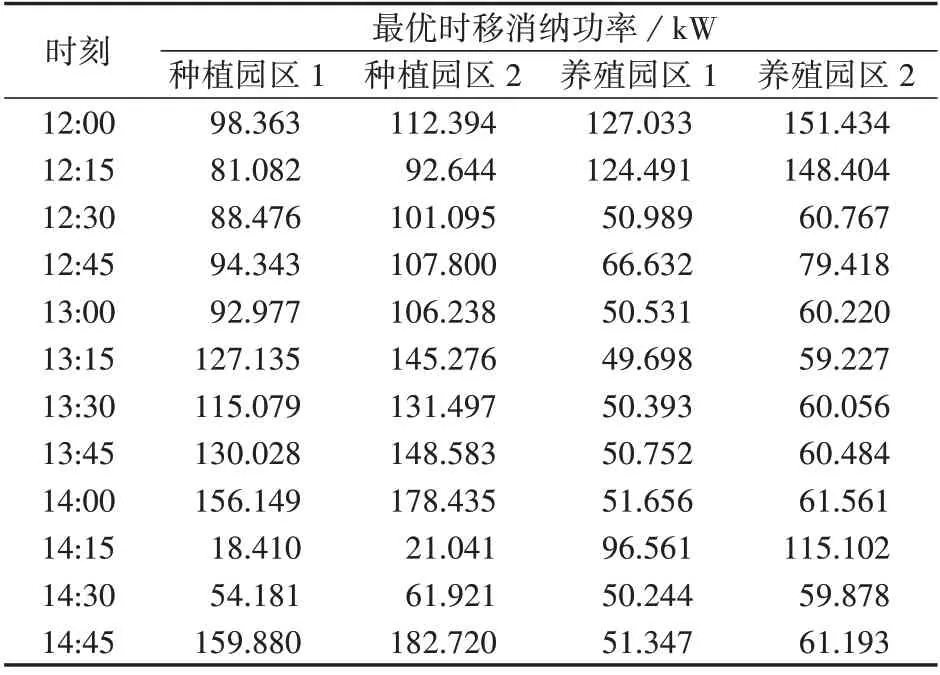
表1 农业园区最优时移消纳功率Table 1 Optimal time-shifted power consumption of agricultural parks

将农业园区部分用电负荷转移至时段TPV后，选择光伏并网节点7、9、15、27、28、32，判断农业园区方最优博弈策略ΩT(ps.best，P)能否维持光伏并网母线电压在允许范围内，弃光电量问题是否得到缓解。在Ω T(ps.best，P)情况下的光伏并网母线如图5所示。

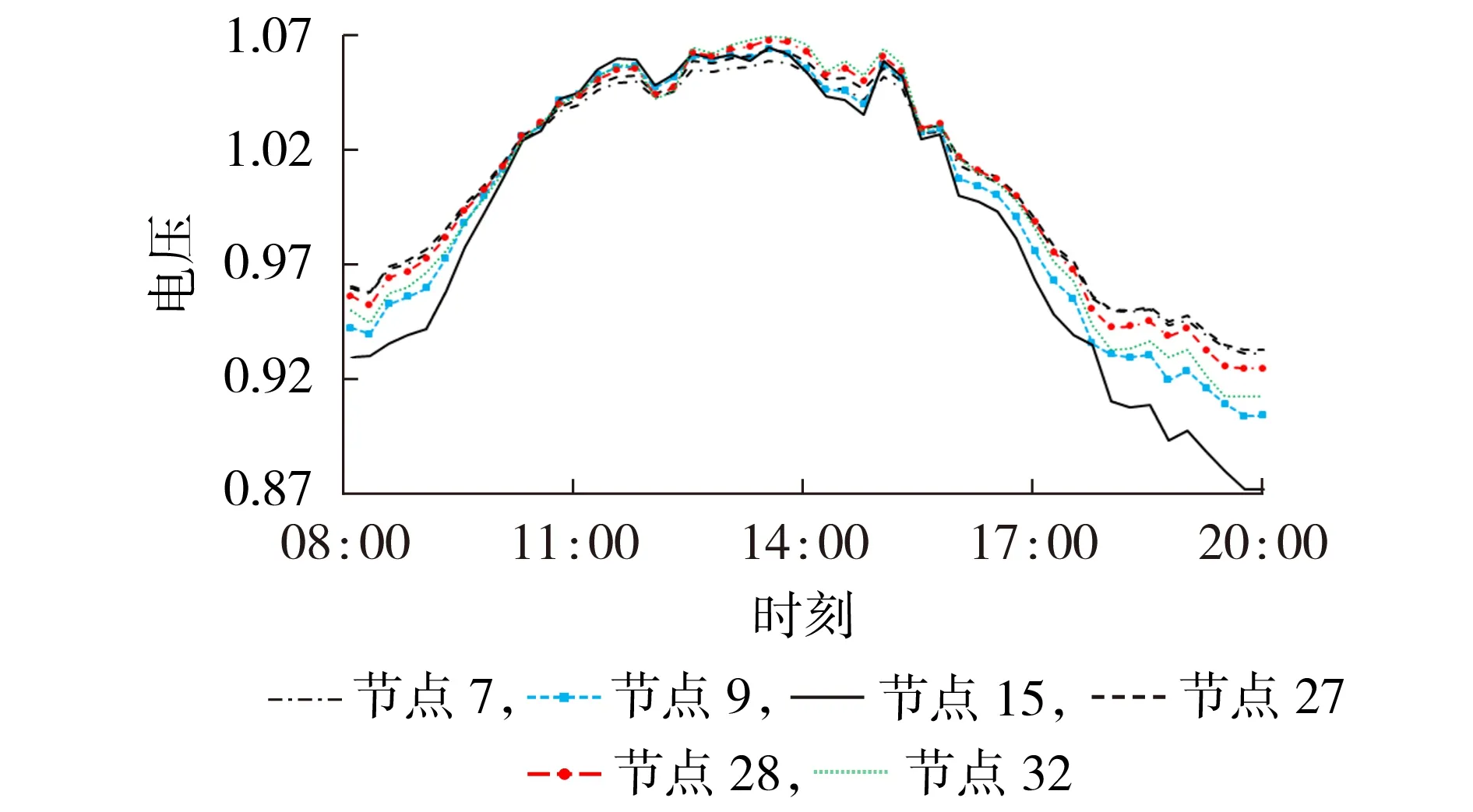
图5 最优博弈策略下光伏并网母线的电压波动Fig.5 Voltage fluctuation of PV grid-connected bus under optimal game strategy

对比图3和图5可知，各农业园区在ps.best的激励下时移自身负荷，就地消纳了分布式光伏发电功率，缓解了光伏并网母线电压越限的问题，增加了光伏电站出力，弃光电量大幅减少。

在农业园区方最优博弈策略下，考虑农业园区用电成本，通常选择将高峰时段的用电设备负荷转移到时段TPV，光伏电站整体就地消纳功率4 413.965 kW。根据高峰时段电价、最优交易电价和最优时移消纳功率，从农业园区整体的用电成本、光伏电站整体弃光电量以及低碳运行效益3 个方面，采用最优交易电价就地消纳模型之后，农业园区和光伏发电方的经济效益如表2所示。

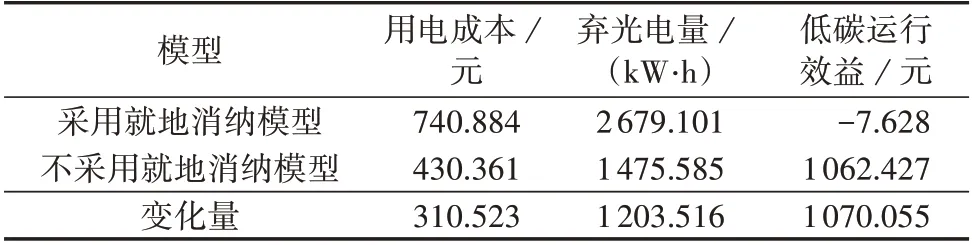
表2 采用就地消纳模型前后的经济效益对比Table 2 Comparison of economic benefits between with and without local consumption model

由表2 可知，采用最优交易电价就地消纳模型可促进农业园区方的就地消纳意愿，光伏电站通过减少弃光电量产生的额外收益为355.037元，增加了低碳运行效益。

3.3 低碳消纳控制仿真

3.3.1 种植园区低碳消纳控制

选取种植园区2 为例进行控制，已知该农业园区冬季最大负荷为400 kW，根据已有种植温室用电信息，确定种植园区2 的规模为10 个设施农业种植温室。采用NSGA-Ⅱ，相关参数如下：种群规模为300；最大迭代次数为200；交叉概率pc=1；变异概率pm=1/xnum，其中xnum为农业园区可供时移设备种类数，种植园区取7。时移设备的功率、数量以及低碳效益见1.1节。

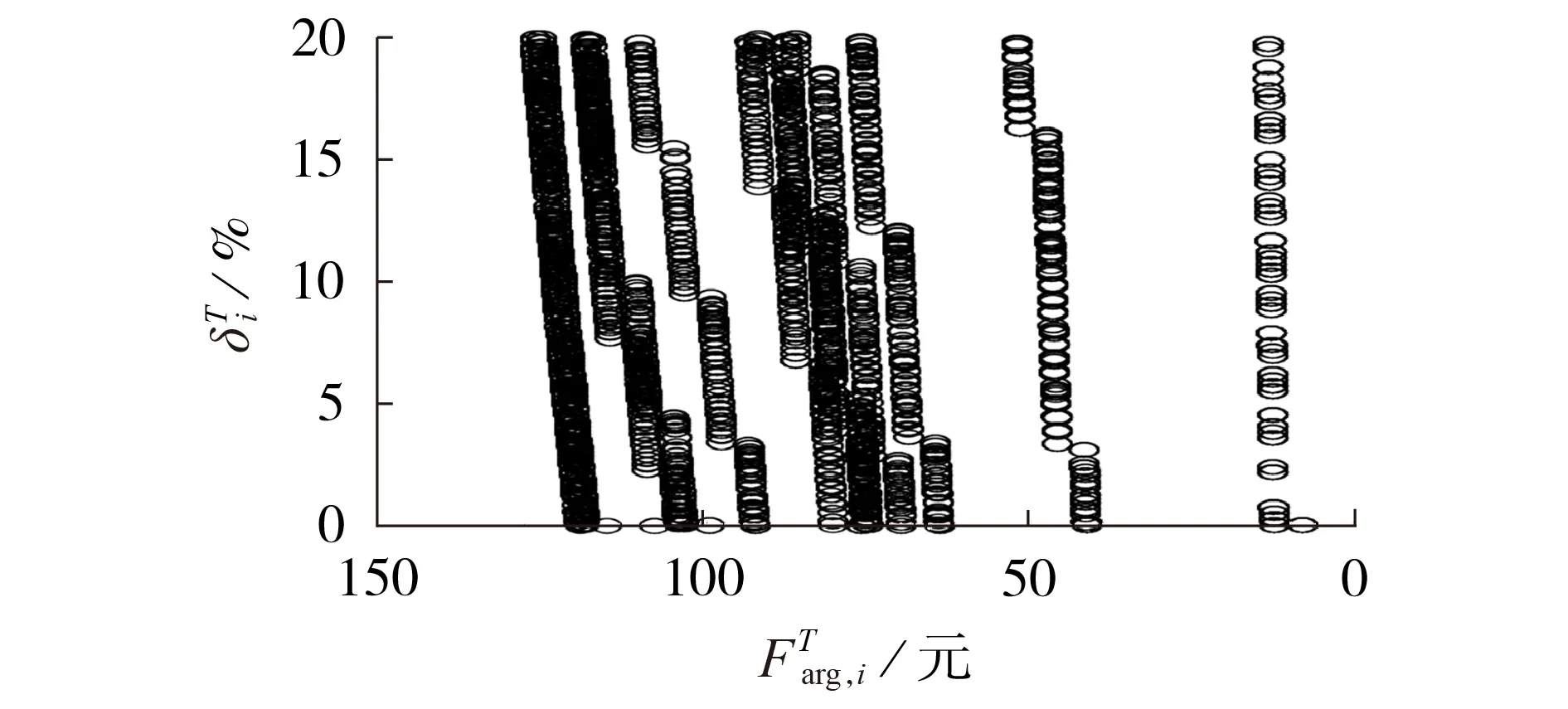
图6 种植园区Pareto前沿Fig.6 Pareto frontier of plantation agricultural park

由图6 可知，种植园区在各计量时段的Pareto前沿变化趋势都是倾向于左下方，表明最优解集在各个计量时段内都互不支配，满足非支配解定义，从而证明采用NSGA-Ⅱ求解出的最优解是可信任的。

3.3.2 养殖园区低碳消纳控制

选取养殖园区2 为例进行控制，已知该农业园区冬季最大负荷为310 kW，根据已有养殖温室用电信息，确定此养殖园区养殖规模为900 头牛。采用NSGA-Ⅱ，养殖园区可供时移设备种类为8，其他仿真参数与种植园区相同。

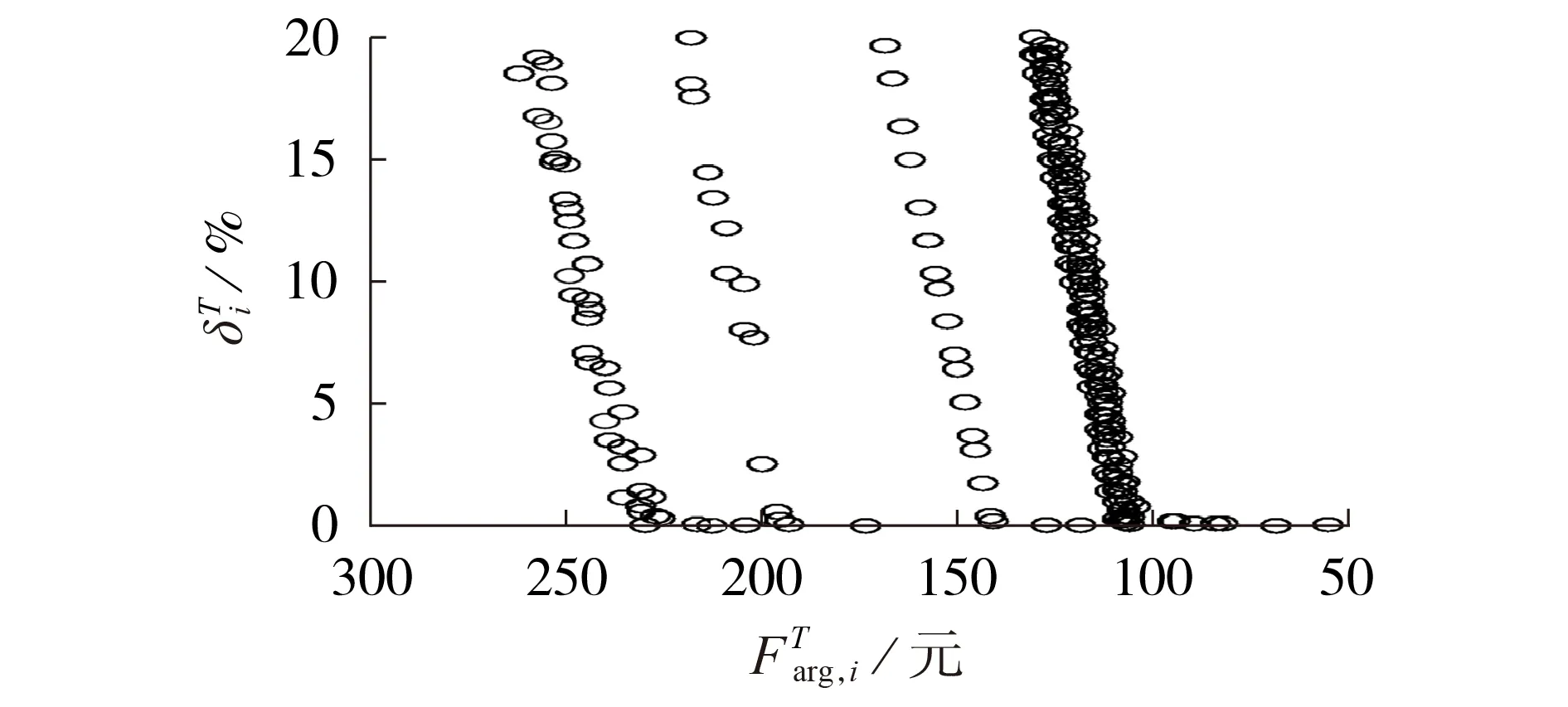
图7 养殖园区Pareto前沿Fig.7 Pareto frontier of breeding agricultural park

4 结论

本文提出了基于Stackelberg 博弈的分布式光伏低碳化消纳方法，构建了低碳化源荷协调双层优化模型以提高配电网的分布式光伏就地消纳能力。通过所建立的最优交易电价就地消纳模型，基于Stackelberg 博弈模型，确定了最优交易电价；通过该交易电价有效促进了农业园区时移负荷消纳光伏电量的意愿。根据不同农业用电设备的低碳效益，在确定最优时移消纳功率的基础上，可以对不同类型的农业园区进行低碳消纳控制；以低碳消纳效益最大为目标，通过就地消纳违约率进行约束，能够获得不同农业园区的最大低碳消纳效益。采用IEEE 33节点配电网进行仿真验证，以光伏发电和农业园区方整体综合收益最大为目标函数，通过光伏并网母线电压波动进行检验，确定了最优交易电价和各农业园区不同时段的最优时移消纳功率。仿真结果表明光伏发电与农业园区各方的收益均得到提高，减少了弃光电量，增加了低碳效益；各农业园区具有就地消纳光伏发电功率的能力，且附加低碳效益得到有效提高。

附录见本刊网络版（http：//www.epae.cn）。