结合Kalman滤波与小波神经网络的沉降形变监测

陈冠宇，胡小伍，洪雪倩，党沙沙，周 吕

（1.浙江省国土勘测规划有限公司杭州分公司，浙江 杭州 310030；2.浙江省测绘科学技术研究院，浙江 杭州 310030；3.桂林理工大学 测绘地理信息学院，广西 桂林 541004）

高速铁路的快速发展，必然伴随着大量隧道工程的涌现，这主要与高速铁路线路技术标准（平纵断面）有关。相较于普通铁路的标准，其以高速度、高稳定性、高平顺性特征著称[1]。隧道是高速铁路线下工程中的重要组成部分，是藏于山体内的连续刚性构筑物，其基底的稳定性对于高速铁路隧道无砟轨道的耐久性以及线路的高平顺性至关重要[1]。为确保高速铁路工程质量和运营安全，对线下工程进行沉降变形观测和分析十分必要，因此本文以某在建高速铁路隧道沉降变形观测数据为例，将结合Kalman滤波的小波神经网络应用于高速铁路隧道的沉降变形分析中。Kalman滤波是一种动态数据分析方法，其计算过程是一个不断修正的过程，通过递推计算的方式获取最新的滤波值，适用于离散性系统，对于消减沉降变形数据中的随机噪声具有较好效果，使沉降变形数据更逼近实际情况。本文通过建立结合Kalman滤波的小波神经网络模型，对比分析了结合Kalman滤波的小波神经网络与单一小波神经网络的预测效果。

1 结合Kalman滤波的小波神经网络与评价指标

将Kalman滤波与小波神经网络有机结合，形成一种结合Kalman滤波的小波神经网络，既能有效消减数据中的随机噪声，又能继承小波神经网络较强的容错性能和逼近能力，从而改善单一小波神经网络的预测效果。

1.1 Kalman滤波

Kalman滤波是一种递推式滤波算法[1]，能剔除随机噪声，获得接近真实情况的有用信号。其算法方程式为[2-4]：

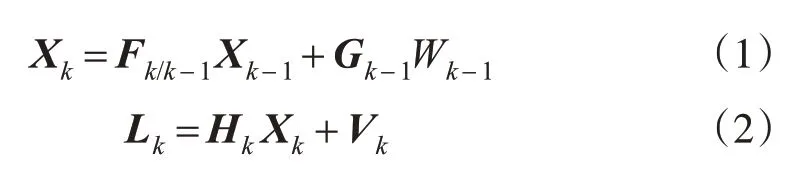
式中，X k为状态向量；F k/k-1为状态转移矩阵；G k-1为动态噪声矩阵；W k-1为动态噪声；L k为观测向量；H k为观测矩阵；V k为观测噪声矩阵；k、k-1分别为k、k-1时刻。

根据最小二乘原理，Kalman滤波的递推公式为[5-6]：

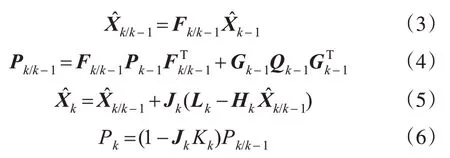
式中，J k为滤波增益矩阵，J k=P k/k-1H kT(H k P k/k-1H kT+R k)-1。

在滤波初值X̂0及其方差阵P0确定的条件下，通过观测值L k递推状态估计值X̂k(k=1,2,3,…)，再基于Matlab编程实现Kalman滤波的去噪效果[7]。

1.2 去噪效果评价指标

1）均方根误差[2]。

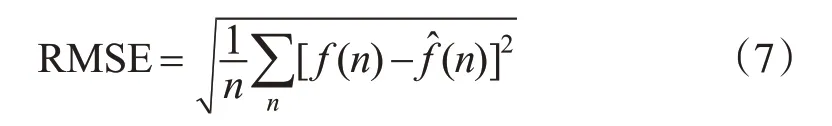
式中，f(n)为原始信号；为去噪后的估计信号；通常RMSE越小，去噪效果越好。

2）信噪比[2]。

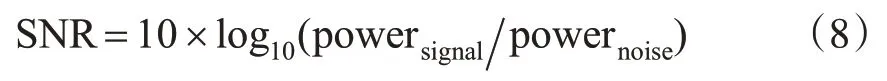
式中，powersignal为真实信号的功率，为噪声的功率，通常SNR越高，去噪效果越好。

1.3 小波神经网络模型

小波神经网络模型是小波理论与神经网络理论有机结合形成的一种新型前馈神经网络模型。它既充分利用了小波分析的局部化性能，又结合了神经网络的自学习能力等优点，具有较好的容错能力和预测效果[2,8]。基于如下学习算法[2,8-9]：

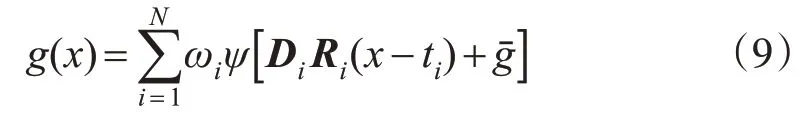
式 中，ψ为R n→R；ψ(x)=ψs(x1)ψs(x2)…ψs(x n)，x=(x1,x2,…x n)；D i、R i分别为对角和旋转矩阵。

为得到一个使其逼近函数f(x)的有效学习算法，设样本组为：

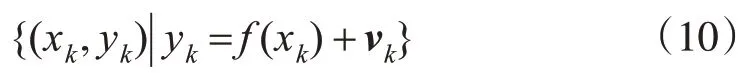
式中，v k为噪声向量。

参数向量定义为：

记g(x)=gθ(x)，则系统误差（单个样本）为：

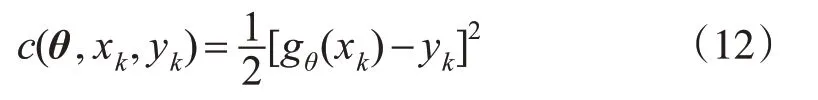
误差的数学期望或平均值为：

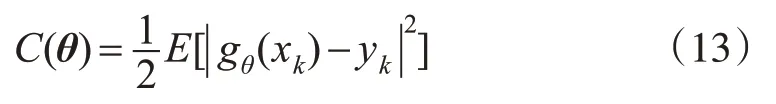
对角阵的两种表示方法为：

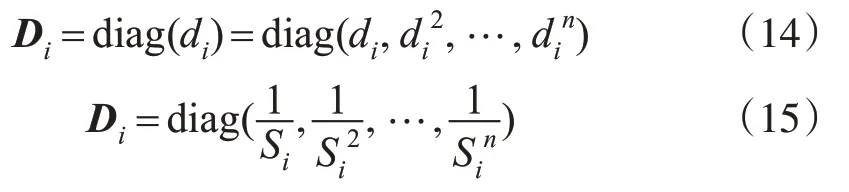
因此，误差函数对它们的偏导数分别为：

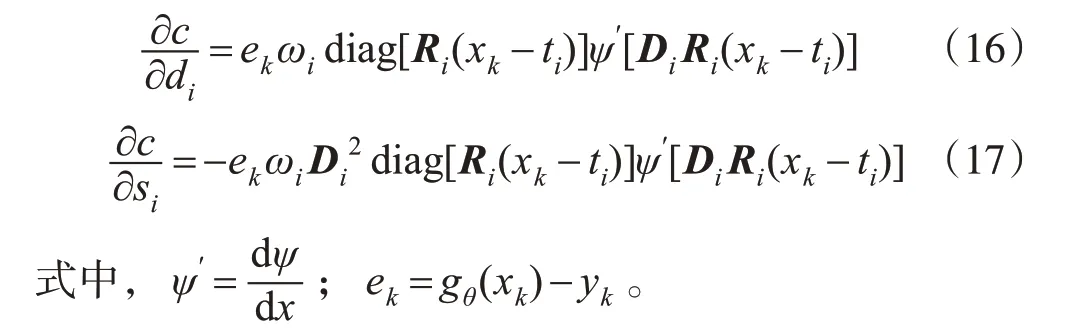
1.4 预测模型精度评定

1）平均绝对误差[2,8]。

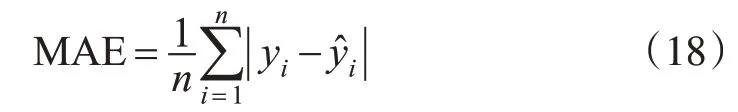
2）均方误差[2,8]。

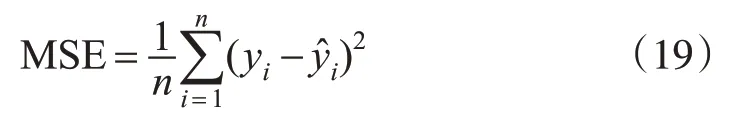
3）模型精度[2,8]。

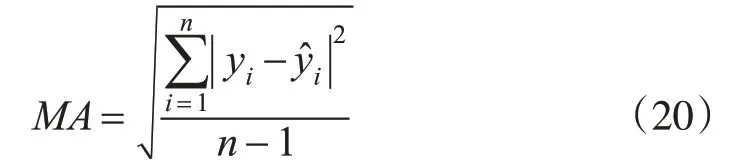
式中，yi为观测值；为预测值；n为观测总数。

通过上述3种模型精度评定指标判定模型预测精度的优劣，数值越小，预测模型精度越高。

2 工程实例

本文以某新建高速铁路线工程某隧道工程一沉降观测点S01的24期实测数据为例，进行沉降变形预测分析。由于隧道工程的特殊结构，沉降变形量相对稳定，变形观测采用三等沉降变形测量（相当于国家二等水准测量要求）。在高精度测量过程中不可避免的受光线强度、温度等多种因素影响，数据中可能含有大量的随机噪声，将对变形预测分析造成较大的影响。本文通过分析高速铁路隧道工程的沉降变形数据特点，引用Kalman滤波对观测数据进行去噪处理，有效剔除观测数据中存在的随机噪声，使观测数据更逼近真实数据，从而提高数据的准确性；再通过小波神经网络模型对Kalman滤波去噪前后的观测数据进行预测分析。

2.1 Kalman滤波去噪

根据《高速铁路工程测量规范》要求，沉降变形测量按高铁沉降三等规定进行周期性监测，确定观测噪声方差阵R k=0.5，因此系统的动态噪声方差阵取Q k=根据前两期观测数据确定初始值然后通过Kalman滤波程序，对沉降观测点S01的24期实测数据进行去噪处理。去噪前后沉降量与精度如表1所示，去噪前后沉降曲线对比如图1所示，可以看出，RMSE为0.081 mm，SNR为34.649 db，说明Kalman滤波能有效消减沉降变形数据中的随机噪声，具有一定的去噪效果；Kalman滤波去噪后能使沉降曲线更平滑、更逼近实际沉降变形情况，对数据中存在的随机噪声消弱效果较好。

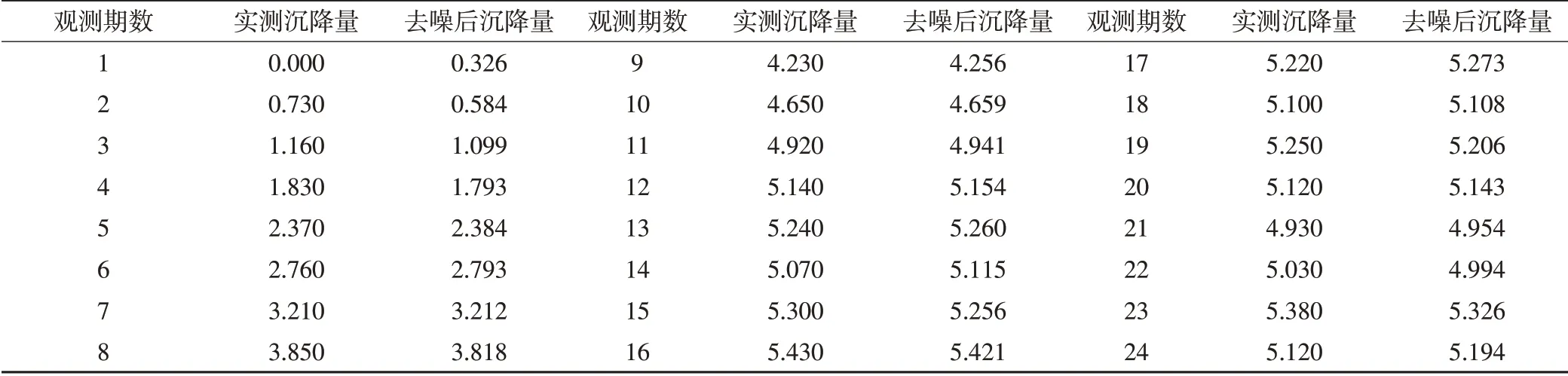
表1 沉降观测点S01去噪前后沉降量与精度/mm

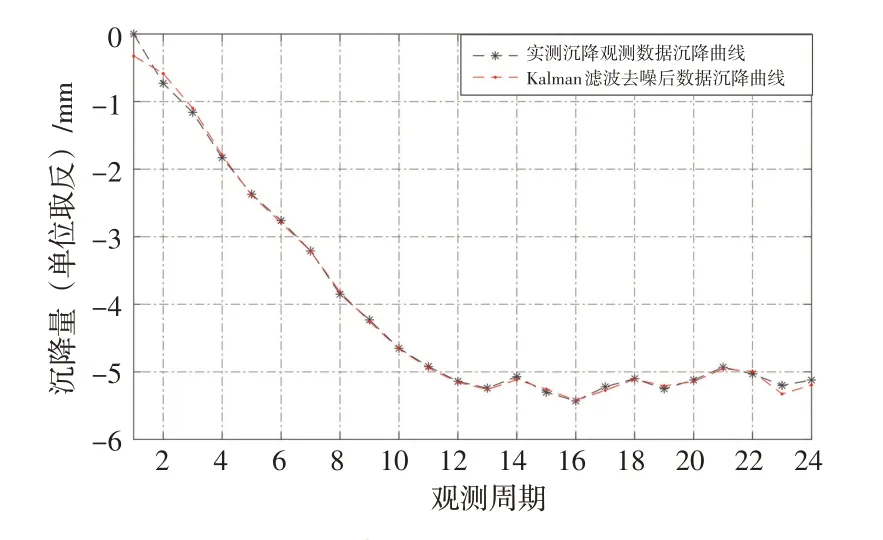
图1 Kalman滤波去噪前后数据对比图

2.2 小波神经网络模型预测分析

本文基于经过Kalman滤波去噪前后的24期观测数据，以前18期观测数据为训练样本，利用小波神经网络模型进行网络训练；以后6期为检验样本，并与后6期的预测值进行对比分析。预测结果分析如表2和图2、3所示，可以看出，去噪前后预测最大残差绝对值分别为0.207 mm和0.153 mm，小波神经网络模型对去噪后的预测值较稳定；去噪前后预测值的MAE分别为0.100 mm和0.092 mm，MSE分别为0.014 mm和0.010 mm，MA分别为0.130 mm和0.110 mm，说明结合Kalman滤波的小波神经网络模型相对于单一小波神经网路模型的预测稳定性和精度均较高，具有一定的优势；结合Kalman滤波的小波神经网络模型预测值以及残差值曲线比单一小波神经网络模型稳定，更逼近真实沉降情况。综上所述，结合Kalman滤波的小波神经网络模型能更好地提高单一小波神经网络模型的预测精度和稳定性，具有较好的应用价值。

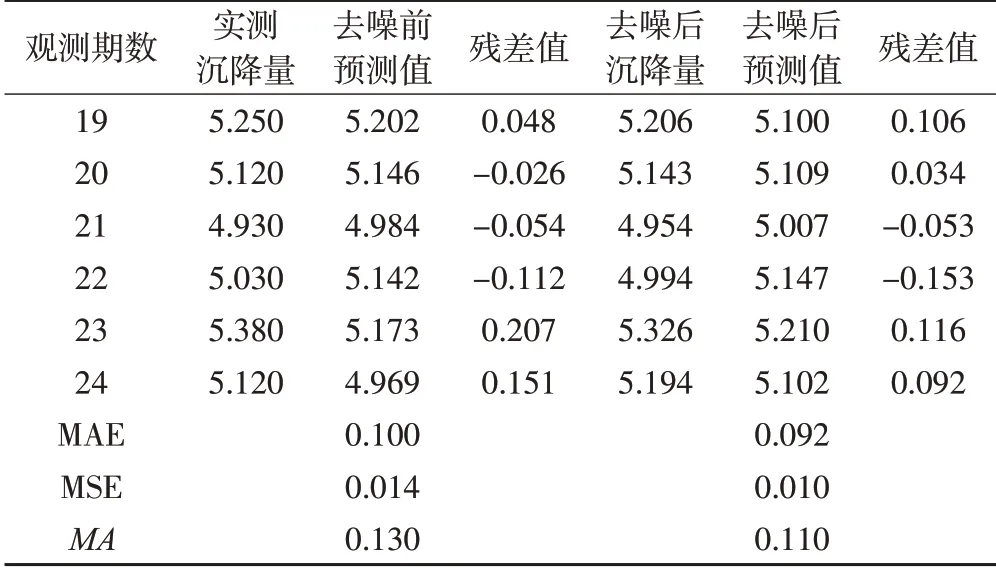
表2 沉降观测点S01去噪前后预测值/mm

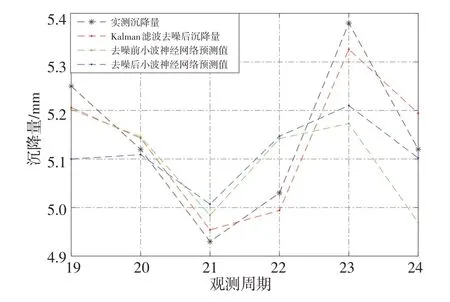
图2 Kalman滤波去噪前后预测对比图

3 结语

通过工程实例分析发现，结合Kalman滤波的小波神经网络模型能有效消减沉降观测数据中的随机噪声，有效提取可靠的变形信息，且较好地继承了小波神经网络的局部化性能和自主学习能力等优点，具有较强的自适应能力，从而提高了预测精度。因此，在变形分析应用中，结合Kalman滤波的小波神经网络模型比单一小波神经网络模型更具优势。